自动化码头考虑缓冲区的设备协调调度优化

秦 琴，梁承姬

上海海事大学 物流科学与工程研究院，上海201306

1 引言

港口作为集装箱运输的交通枢纽，主要起到集装箱的中转作用。集装箱码头作为港口的重要部分，其作业效率直接影响着港口运营效益。近年来，随着集装箱港口的设备升级，码头的自动化程度有了很大提升，甚至出现了全自动化的集装箱码头，使码头作业效率实现了质的飞跃。根据主要的自动化设备可以将码头作业系统分为双小车岸桥作业子系统，AGV（自动导引车，Auto‐mated Guided Vehicle）作业子系统和ARMG（自动化轨道吊，Automated Rail Mounted Gantry Crane）作业子系统，三个子系统之间环环相扣，协同作业。集装箱码头运作成本和运行效率很大程度上取决于码头作业系统各环节之间的协调调度，研究这三种设备的协调调度对于自动化集装箱港口运作优化有着重要意义。

关于码头作业系统的优化研究，国内外相关专家学者做出了重要贡献，目前主要分为两个子系统之间的协同调度优化[1-3]以及三个子系统之间的集成调度优化[4-5]。Niu 等[1]在考虑准备时间的前提下研究了集卡调度与堆存问题，并使用粒子群算法和细菌部落优化算法求解问题。周静娴等[2]研究了自动升降车与岸桥的协同调度问题，针对自动升降车的任务序列进行优化，并得出不同情况下的最优作业顺序和作业成本。曹朋亮等[3]综合考虑场桥安全距离，任务优先级等现实约束，建立了装船时间最小化的场桥与集卡的联合调度模型，通过遗传算法求解以及实证分析，证明在集卡数量较少时，作业面模式能有效减少装船时间。栾晨等[4]将双循环模式下的岸桥，AGV 与场桥集成调度问题抽象为混合整数规划模型，以基于启发式的自适应遗传算法作为求解方法对任务完成时间进行了优化。Xin 等[5]研究了岸桥、AGV 和ASC（自动堆垛机，Automated Stacking Crane）三者之间的协调调度，在AGV 路径规划上利用分层控制构架，提出一种生成AGV 自由无碰撞路径的方法以避免AGV之间的碰撞。

随着对自动化集装箱码头装卸设备调度优化的不断深入，缓冲区也越来越受到相关学者的关注，分别为双小车岸桥的缓冲区（中转平台）[6-8]和堆场中的缓冲区（缓冲支架或AGV 伴侣）[9-10]。丁一等[6]在考虑双小车岸桥中转平台的情况下，对后小车进行作业时间窗约束，通过Cplex求解验证了带有中转平台的双小车岸桥对于AGV 调度的优越性。唐世科等[7]以最小化完工时间为目标，建立了带有时间窗约束的双小车岸桥与AGV 协调调度模型，为集装箱任务在中转平台上设置了时间窗，利用遗传算法对实际算例进行了求解分析。梁承姬等[8]在考虑中转平台及其容量限制的情况下，以门架小车时间窗为约束建立AGV 与双小车岸桥的调度模型，并用遗传算法得出AGV 与岸桥两大设备的调度方案。程聪聪等[9]将AGV伴侣的容量约束转化为时间窗约束，以启发式算法求得AGV 伴侣的时间窗，粒子群算法得到AGV调度方案，结果表明AGV伴侣能有效提高AGV与场桥之间的协调性。添玉等[10]针对自动化集装箱码头一种自带提升功能的AGV（L-AGV）和缓冲支架系统，提出了新的设备集成调度框架，并设计了双层遗传算法对模型进行求解。

综合以上所述研究现状，关于自动化集装箱码头缓冲区的研究基本集中在岸桥缓冲区与水平运输设备AGV 或ALV 的集成调度方面，少数文献对于堆场海侧交接区设置固定的集装箱缓冲支架进行了考虑，但同时考虑岸桥缓冲区与堆场缓冲区的设备集成调度问题尚未见到。本文的创新在于研究双小车岸桥，AGV和ARMG三种设备集成调度的同时，充分考虑岸桥中转平台和缓冲支架的缓存作用，并应用缓存有限的柔性流水车间调度理论（Limited-Buffer Flexible Flow-shop Scheduling Problem，LBFFSP）[11-13]将缓冲区和装卸搬运设备作为整体进行调度优化，这对增强设备间的协调性，提高AGV的使用效率有着重要作用。

2 问题描述

图1展示了一种自动化码头“双小车岸桥+AGV+缓冲支架+ARMG”的装卸工艺。以进口集装箱为例，其作业流程主要包括双小车岸桥操作，AGV 水平运输以及ARMG堆存三个阶段，相邻两阶段之间均设置有容量有限的缓冲区。第一阶段，双小车岸桥作业阶段，岸桥主小车从集装箱船上抓取集装箱放置到岸桥中转平台处，岸桥门架小车将中转平台处的集装箱抓取放置到岸桥下方的AGV 上；第二阶段，AGV 水平运输阶段，AGV 在基于作业面的作业模式下将集装箱运输到指定箱区，并将其放置到箱区前方的缓冲支架上，而后即可离去执行下一个任务；第三阶段，ARMG 堆存阶段，ARMG 从缓冲支架上抓取集装箱，按照堆存计划将其放到箱区指定位置上。在这种装卸工艺下，双小车岸桥的中转平台以及堆场箱区海侧的缓冲支架充当容量有限的中间缓冲区，有利于提升AGV 水平运输与岸桥装卸和ARMG 装卸作业间的协调性，减少了设备间的相互等待时间。

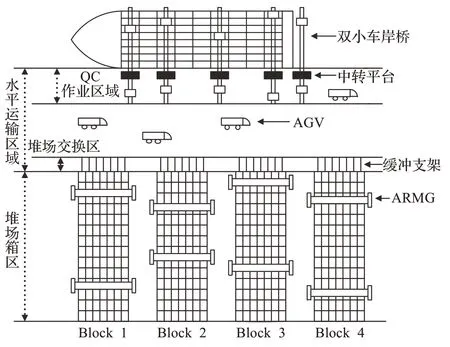
图1 一种带有缓冲区的自动化码头示意图

针对以上所述装卸工艺，本文通过引入一种带有限中间缓存的柔性流水车间调度理论（LBFFSP）来综合考虑双小车岸桥、AGV、缓冲支架和ARMG 的三阶段集成调度问题。可将自动化码头作业系统抽象为：如图2，n个待加工工件在车间等待进行m 道工序的加工，m 道工序中每道工序均具有多个并行工位，每个工件只需在每道工序的其中一个工位上加工即可。相邻两道工序间存在容量有限的缓冲区，工件完成前一道工序即可进入缓冲区等待下一道工序的开始，若缓冲区容量已满，则产生阻塞，直到该缓冲区有存放空间。

图2 带有有限缓冲区的柔性流水车间模型

由于码头作业的特殊性，其区别之处主要在于：

（1）集装箱任务之间的预定义顺序约束，如卸船时，靠岸侧任务优先于靠海侧任务。

（2）多台岸桥同时作业，避免交叉碰撞。

（3）设备必须移动到指定位置才能进行作业。

3 自动化设备的集成调度模型

3.1 模型假设

（1）所有待作业的集装箱均为20英尺标准箱。

（2）船舶配载计划与堆场堆存计划均已知。

（3）不考虑翻箱问题。

（4）设备作业时间包含设备调整时间和操作时间。

（5）同一阶段的并行设备作业能力相同。

3.2 模型参数及决策变量

（1）参数

J：集装箱任务集合J={1 ,2 ,…,j}，虚拟任务j=0 为所有设备的第一个任务。

JP：预定义顺序约束集合，如( j,j′ )∈Jp表示任务j必须在任务j′之前开始作业。

M：设备集合，i ∈M 为所有设备索引，Mk表示第k阶段的设备集合，k ∈{ }1,2,3。

Bj：集装箱j在船上的所在贝位号。

Li,( i ∈ M3)：表示该ARMG 所在箱区的最大堆存容量。

Buk：表示第k阶段前的缓冲区，k ∈{2 ,3}。

bck：表示Buk的容量，k ∈{2 ,3}。

buk,l：表示Buk中的缓冲工位l,l ∈{1 ,2 ,…,bck}。

Tej,k,l：集装箱进入缓冲工位buk,l的时间。

WAk(t)：表示t时刻缓冲区Buk中等待作业的队列。

H：一个足够大的正数。

（2）决策变量

uj,j′,k,i：第k 阶段，集装箱j在j′之前由设备i操作（连续）时为1，否则为0。

OAj,k(t)：t 时刻，集装箱任务j 在WAk(t )队列中为1，否则为0。

3.3 目标函数及约束

式（1）为目标函数，即最小化最大完工时间；式（2）定义作业系统的makespanCmax；式（3）规定操作Oj,k在第k 阶段有且仅有一台设备i 处理；式（4）表明每个操作的完成时间和作业时间之间的关系；式（5）规定虚拟任务n在第k 阶段的完工时间为0；式（6）～（8）定义yj,j′,k,i，当xj,k,i=xj′,k,i=1 时，yj,j′,k,i=yj′,j,k,i=1；式（9）和（10）规定了zj,j′,k,i和uj,j′,k,i；式（11）和（12）表明所有任务j ∈J 在JP上都有一个紧前和紧后任务；式（13）和（14）确定xj,k,i与uj,j′,k,i和uj′,j,k,i之间的关系；式（15）明确同一设备的两个连续任务之间的顺序关系；式（16）明确同一任务在连续两个阶段的操作顺序约束；式（17）和（18）定义vj,j′；式（19）为岸桥避碰约束，式（20）为堆场容量约束；式（21）规定任务进入缓冲区的时间要大于等于其在上一阶段的完工时间；式（22）表明在t 时刻缓冲区中等待处理的队列中包含的所有任务；式（23）是缓冲区容量有限约束，任意时刻WAk(t )中的任务总数要小于等于该缓冲区最大容量bck。

4 基于遗传算法的调度算法

上述模型描述的调度问题属于NP-hard 问题，随着问题规模的增大，计算复杂度将呈指数增长，而遗传算法（Genetic Algorithm，GA）以其简单通用、鲁棒性强、并行处理广等特点在求解此类NP-hard 问题上优势明显，其良好的全局优化能力使得其在求解大规模复杂问题方面快速高效，在设备调度问题和柔性流水车间调度问题上都具有重要的应用价值。NEH 启发式算法是由Nawaz、Enscore 以及Ham 于1983 年提出的高效性构造型算法[14]，具有很强的局部搜索能力。综合GA 的全局优化特点和NEH 的局部寻优特点，本文采用NEH 启发式算法产生初始解，加入到GA 中，以提高算法性能，算法流程如图3所示。

图3 算法流程图

4.1 染色体编码与解码

本文采用基于操作的编码方式，取所有集装箱任务序号的一种排列组合作为一个染色体，集装箱编号即是构成染色体的基因值。例如：有10 个待处理的集装箱，对于这10 个任务可以取P1=[ ]2 9 6 3 7 8 2 4 1 5 10 作为一个染色体个体，集装箱编号在染色体中的位置即为集装箱任务的优先级顺序，这种编码方式搜索空间较小，易于操作。

本文采用NEH启发式算法来生成初始解，使得生成的个体更接近最优解，进化效果更好，其基本原理如下：

步骤1由于已知船舶配载计划与堆场堆存计划，可以估算出每个待卸集装箱完成三个阶段所有操作所需的总加工时间，并按降序排列。

步骤2单独考虑该序列中加工时间最大的两个集装箱，以最小化完工时间为目标对它们进行排序，形成新的序列。

步骤3依次选取剩下的集装箱任务，插入到新的序列中，遍历新序列中每一个可插入的位置，确定总完工时间最小的排序，直到所有任务都被选取过，即可得到一个染色体个体。

重复执行以上所有步骤Psize遍，生成规模为Psize的初始种群。

解码方法：

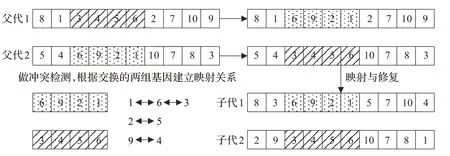
图4 染色体交叉操作示意图

将一个染色体的基因序列按照一定的设备分配规则依次分配到各级设备上，形成一个可行的调度方案的过程称为解码。

最先空闲设备分配规则（FAM）是一种非常有效的设备分配规则，在分配时只要有设备可用，并且缓冲区内有待处理的集装箱任务，就可以使用FAM 规则将缓冲区中优先级最高的任务分配给最先可用的设备，当有多个设备可用时，随机选择一台设备。由于第二阶段集装箱被AGV 运输到不同的箱区，作业时间差别较大，可能会产生空闲时间，在设备分配时考虑在可能的情况下，将任务插入到这些空闲时间内，从而减少总完工时间。

步骤1判断任务在各阶段各设备上最早允许作业时间，零时刻到该设备的释放时刻间的空隙能否插入该任务。

步骤2根据各设备的最早允许作业时间，选择时间最早的设备i对任务j进行加工，并更新设备i上的任务队列，如果没有进行任务插入则更新设备i 的释放时间Cj,k。

步骤3判断所有任务是否在每个阶段都进行了设备选择，是则结束，更新工件在各阶段各设备上的Cj,k；否则返回步骤1。

任务j能否插入空闲时段[ ]

a,b 的条件为：

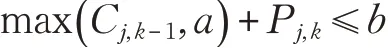
4.2 适应度函数设置

fitness=1/Cmax其中，Cmax表示所有集装箱任务的一个调度方案的最大完工时间。

4.3 遗传操作

选择复制：精英保留，每个染色体个体被保留的概率与其适应度函数值大小成正比，优先选择适应度大的个体，最终选取10%的父代最优个体和90%的新生个体形成新种群。

交叉算子：部分映射交叉（Partial Mapped Crossover，PMX），根据交叉概率从种群中选取两个父代个体，随机选取两个交叉点，将两个交叉点之间的基因片段根据映射关系进行替换，即可得到新个体，交叉操作如图4所示。

变异算子：两点交换，如图5，根据变异概率选取一个父代染色体，随机选取该染色体上两个不同基因位置，交换这两个位置上的基因，即能变异得到新染色体。

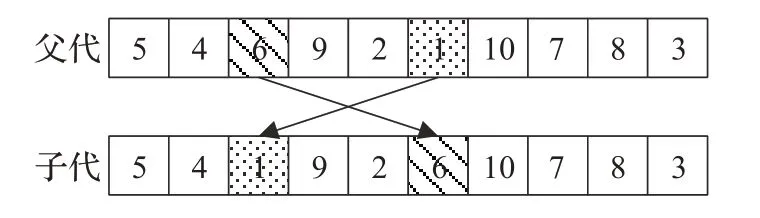
图5 染色体变异操作示意图

5 数值分析

5.1 GA的参数设置与初始解对比

参数设置对GA 算法性能有重要影响，问题类型的不同导致算法参数的选取存在差异。为找到适当的参数，基于算法的收敛性和算法运行时间进行了同一问题的多次实验，实验结果如表1 所示，在所有备选参数中，当交叉概率Pc=0.9，变异概率Pm=0.2时算法性能最佳。

优质的初始种群能够提高GA 的全局收敛性，使其更快地到达最优解。为验证NEH 启发式算法产生初始种群的遗传算法相较于传统遗传算法的优越性，进行了初始解对比实验，将NEH 产生初始种群解的质量与随机产生的初始种群解的质量进行对比，作为NEH 启发式算法产生初始解的质量的客观依据。每个实验重复10 次，分别记录初始种群最优解和解的均值，实验结果如表2 所示，A 表示NEH 初始种群最优解，B 表示随机初始种群最优解，C 表示NEH 初始种群解的均值，D 表示随机初始种群解的均值。

相同条件下的10 次实验中，采用NEH 产生的初始种群最优解的平均值为35.75 min，解均值的平均值为42.1 min；随机产生的初始种群的最优解的平均值为40.78 min，解均值的平均值为49.55 min，由此可知，NEH 产生的初始种群解的质量明显优于随机产生的初始种群解的质量，很大程度地提升GA 性能，使其更符合本文的计算要求。

表1 GA参数设置

表2 初始种群对比实验 min

5.2 有限缓冲区情况下的算例分析

某集装箱港口的自动化码头现需使用6 台双小车岸桥，20 辆AGV，对某艘集装箱船上的300 个进口集装箱进行卸载作业，根据堆场堆存计划已知这300 个进口集装箱分布在堆场的15 个不同的箱区中，即需要使用15 台ARMG 对其进行堆存作业。其中，双小车岸桥主小车卸载一个标准箱的时间固定为110 s，门架小车卸载一个标准箱的时间固定为60 s，AGV 的行驶速度为8 m/s，AGV 到达指定位置后处理集装箱的时间为20 s，ARMG 处理一个标准箱的时间固定为80 s。双小车岸桥中转平台缓存容量为2 个标准集装箱，堆场箱区海测的缓冲支架容量为5 个标准集装箱。集装箱船到堆场各箱区的距离矩阵如表3所示。

GA 相关参数设置如下：种群规模Psize=100 迭代次数gen=500,交叉概率Pc=0.9,变异概率Pm=0.2。NEH启发式算法以及GA 的程序均是通过Matlab2016b 仿真软件实现，运行于Windows 8 操作系统，处理器为In‐tel®CoreTMi3，CPU2.50 GHz，内存为4.0 GB 的PC 机上。

通过程序运行，得到GA 的收敛情况如图6所示，最终得到的最优完工时间约为9 847.3 s，双小车岸桥的调度方案以及任务排序如表4 所示，表5 为ARMG 的堆存作业调度方案，AGV 的指派结果如表6 所示，表7 为优化前（无缓冲区）与优化后（有缓冲区）的完工时间的对比。

表3 船舶到各箱区的距离 m

表4 双小车岸桥作业调度结果

表5 ARMG作业调度

图6 遗传算法收敛图

表6 AGV指派结果

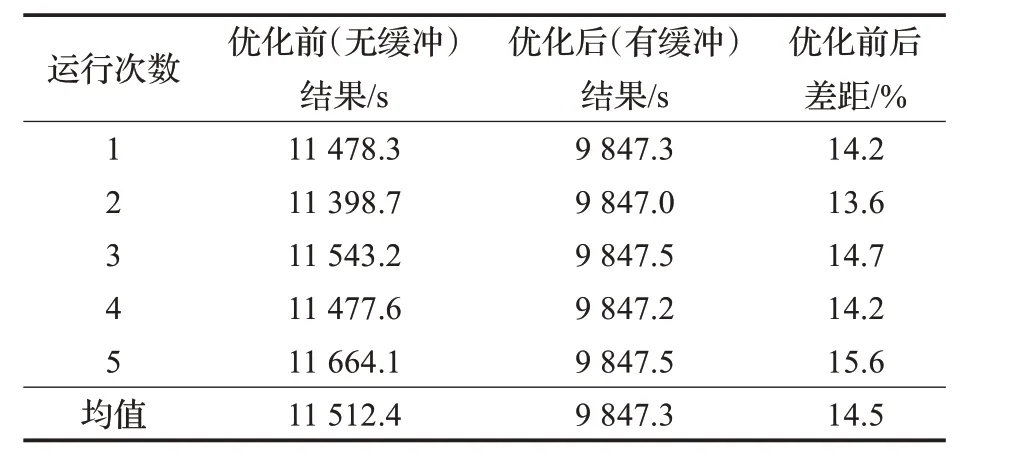
表7 优化前后完工时间比较

由表7 的优化前后完工时间的对比结果可以看出，在船舶配载计划与堆场堆存计划均已知的情况下，缓冲区的设置能显著减少完工时间，表4～6 的调度结果也可以看出，设置缓冲区不仅使各阶段的各台设备间的运作衔接更加流畅，也使每台设备在整体作业中被分配的任务更加均衡，一定程度上避免了某台设备长时间被闲置或某些设备高负荷作业所产生的资源浪费以及完工时间延长等现象。

5.3 算法比较

前文利用改进遗传算法得到了较大规模算例的调度结果，本节为进一步验证本文提出的集成调度模型与算法的合理有效性，引入粒子群算法（Particle Swarm Optimization，PSO），将其运算结果与GA 的结果进行对比分析。PSO 的种群规模Psize=100，最大迭代次数gen=500，采用Eberhart 等[15]推荐的参数，惯性权重ω=0.729 8，加速常数c1=c2=1.496 18，GA 的实验参数延续前文的设置，两种算法中缓冲区容量设置情况相同。根据所需处理的集装箱量的多少以及所需装卸设备的数量的大小，分别设计9 组小规模算例实验和9 组大规模算例实验，通过对比不同规模下的算例实验来比较GA 与PSO 在实验结果上的差异，包括算法得出的完工时间与算法运行所需的时间，每组实验均运行5 次，实验结果取平均值。

两种算法的对比结果如表8，表9 所示，T、Q、R、V 分别表示集装箱、双小车岸桥、ARMG与AGV的数量。小规模算例实验下，PSO的运行时间普遍比GA长，但是两种算法得到的完工时间都相差不大，GA的优势不明显；相较于小型问题，大规模问题下遗传算法的高效性更加明显，9组大规模算例中，不论是完工时间还是算法运行时间，GA都明显优于PSO。综合以上分析可以说明，就本文所研究的问题而言，遗传算法是一种高效可行的求解方法，通过与PSO的结果对比也证明了本文提出的包括缓冲区在内的多设备集成调度模型与算法能有效满足自动化码头集成调度的要求。

5.4 缓冲区容量对完工时间的影响分析

为了评估不同任务规模下随AGV 数量的增多，缓冲区容量的设置对于整个调度的完工时间的影响，分别进行以下两组实验，较小任务规模实验与较大任务规模实验，每组包含3 个缓冲区容量设置不同的实验，每个实验在Matlab 中分别运行10 次，取最大完工时间的平均值作为评价指标，其中bc2表示岸桥中转平台容量，bc3表示缓冲支架容量。

表8 小规模问题算法求解结果对比

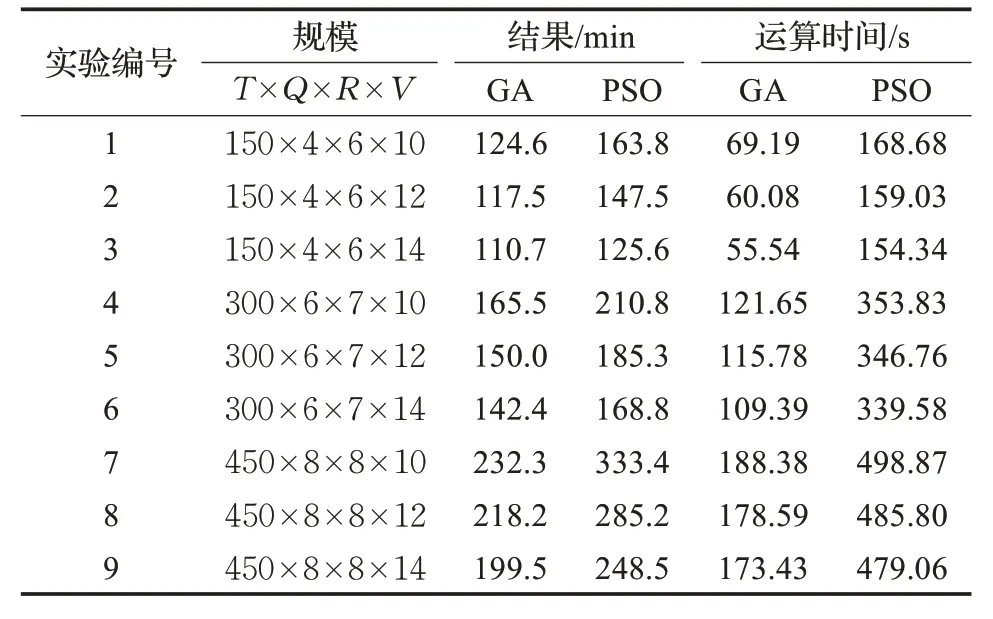
表9 大规模问题算法求解结果对比

小规模实验：60 个标准箱，2 台双小车岸桥，5 台ARMG，AGV 数量为3～10 辆；大规模实验：400 个标准箱，8 台双小车岸桥，14 台ARMG，AGV 数量设置为10～20辆。

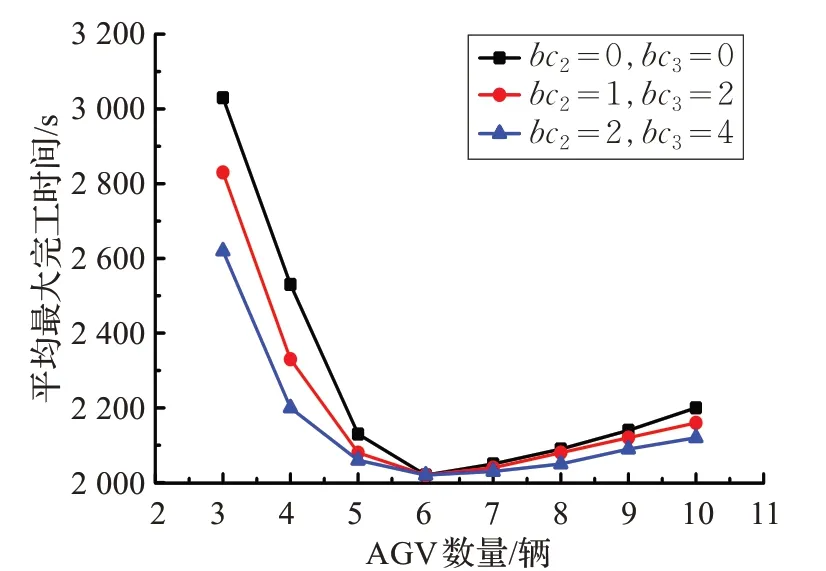
图7 不同缓冲容量的比较（小规模）

图7 为小规模实验结果，从横向看，当缓冲区容量固定时，随着AGV 数量的增多，完工时间逐渐减少，但当AGV 数量达到6 辆时，不论缓冲区容量是多少，平均最大完工时间不变或变化甚微，因为此时的AGV 数量足够多，可以通过AGV 调度满足岸桥与ARMG 的作业需求。此后，完工时间随AGV 数量增大反而逐渐上升，但是增加幅度较小，这是因为AGV 数量过多时，受双小车岸桥和ARMG 装卸能力的限制以及缓冲区容量的限制，AGV 到达中转平台下方时需要等待岸桥卸载集装箱，AGV 运输集装箱到达指定箱区时，需要等待ARMG可用或缓冲支架可用，其中造成的等待时间增加了整体作业的完工时间。纵向来看，当AGV 数量固定时，随着缓冲区容量的增大，平均完工时间得到有效减少，当AGV 数量较少时这种现象尤为明显，因为缓冲区容量越大暂存的集装箱越多，AGV 到达时不必等待双小车岸桥与ARMG，直接取走或放下集装箱即可，减少了设备之间的等待时间。

从图8 中可以更加清晰地看出，当作业量达到一定规模时，缓冲区及其容量的设置对于完工时间的优化效果更为明显。AGV 数量为17 辆时，缓冲区设置为bc2=3,bc3=6 的实验的完工时间达到最优，11 450 s 左右，相比缓冲区为bc2=0,bc3=0 的实验结果，优化了1 120 s 左右，相比缓冲区为bc2=2,bc3=4 的实验结果，优化了约456 s。但由于缓冲区容量有限，AGV 数量超过17辆后，设备等待时间增多导致完工时间增大。

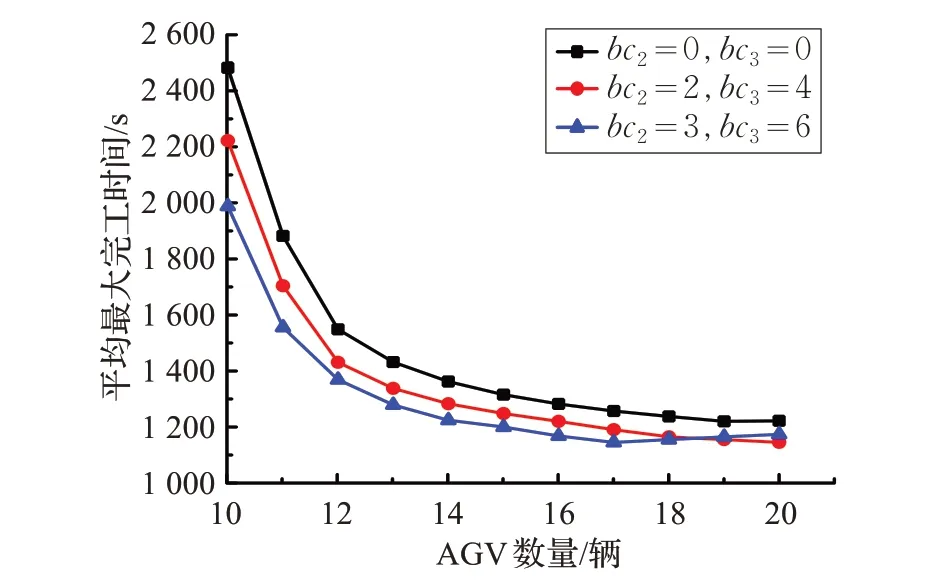
图8 不缓冲区容量的比较（大规模）

综合两组实验的结果可以说明，缓冲区的合理设置使得集装箱码头各种设备资源间的协调性增强，有效减少了船舶在港作业的完工时间，提高了AGV 的使用率，减少AGV 的使用量，从而在一定程度上降低了码头拥堵的可能性。

6 结语

本文主要研究了自动化码头带有缓冲设置的多设备集成调度问题，以缓冲有限的柔性流水车间为基础建立了混合整数规划模型，使用改进的遗传算法进行求解，算例分析与算法对比的结果表明，本文的模型与算法能够有效提高码头运作效益：（1）相较于普通装卸工艺，“双小车岸桥+AGV+缓冲支架+ARMG”这种带有缓冲区的装卸工艺能有效减少完工时间；（2）缓冲区的合理设置不仅能提高设备间的协调性，还能减少AGV 的使用数量，为集装箱码头降本增效。

自动化码头存在各种复杂多变的不确定性，这些不确定因素都会对作业效率产生影响，本文的研究未能将这些随机因素考虑在内，例如堆场内的交通拥堵，AGV的速度变化等。未来关于自动化码头新型设备的调度研究可以将这些不确定因素柔性化，利用柔性调度理论考虑码头的动态性，不确定性和复杂性，可以使研究更具现实意义。