基于GPS的高程拟合方法研究

刘盟　辛修建

摘要：随着科学技术的发展，GPS已经完全应用到测绘行业，如何利用GPS的大地高得到点位的正常高是测绘界研究的重点内容之一，文章在介绍高程系统的基础上，对常用的几种高程拟合方法进行了研究，并对其适用性做了分析和总结，以便更好的应用于高程测量工作中。

关键词：GPS;高程信息;高程系统;高程拟合

一、引言

传统测绘高程外业测量作业中，几何水准测量是比较常用的方法，其测量结果是点位的正常高，该方法具有精度高的特点，但其作业效率低、费时、费力，同时作业条件艰苦，野外作业强度大，虽然随着电子水准仪的问世，几何水准测量的效率有所提升，但是在一定程度上其仍然受到诸多因素的影响，在一些地形变化较大的地区要实施该测量方法就比较困难。另一种是三角高程测量方法，此方法较之水准法来说，测量方式比较灵活，效率高，特别适用于高差较大的地区，跨河测量等，但是这种测量方法最大的局限性是测量两点之间的距离不能太大，如果距离太远将会受到地球曲率的影响，导致测量精度降低。

二、GPS高程测量原理

GPS定位技术是把GPS卫星看作是动态的已知点，通过利用GPS星历提供的卫星瞬间的位置，以GPS卫星和用户的GPS接收机天线相位中心之间的距离为观测量，进行空间距离的后方交会，测出地面点的三维坐标，对于GPS高程的测量是直接利用全球定位系统测量技术，并通过GPS网平差可以得到精度较高的大地高。

GPS通过定位得到的结果属于全球协议地心坐标系，而实用的测量坐标系属于国家大地坐标系或地方独立坐标系，要利用GPS所得数据，就必须对这些数据进行转换，目前国内主要是通过利用一些已知点的高程异常来拟合出某区域内的所有高程异常分布，再将GPS所测的大地高利用拟合公式以及正常高与正高的关系转换成为工程实践当中所需的正常高。大地水准面是一个变化的曲面，点位不同点位高程异常值也不同，因此目前GPS大地高与正常高相互转换的关键在于如何获取高精度的点位高程异常值。

三、高程转换关系

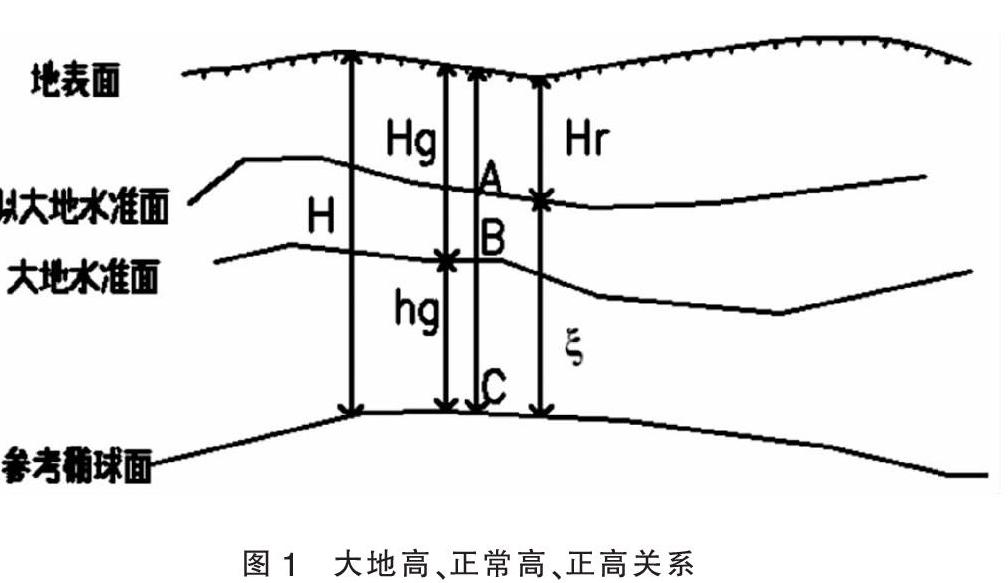
大地高由两个部分组成，分为地形部分和大地水准面（或似大地水准面）高部分，其中我们习惯的把大地水准面的高度叫做大地水准面差距（大地水准面到椭球面的距离），记为hg。把似大地水准面高度叫做高程异常（似大地水准面到椭球面的距离），记为ξ，其具体转换关系见图1。

大地高与正高之间的关系可以表示为：

H=Hg+hg（1）

大地高与正常高之间的关系可以表示为：

H=Hr+ξ（2）

四、高程拟合方法

目前，在工程测量施工当中，由于GPS水准测量方法能够大大减少工期、降低费用，所以在高程测量方面被广泛应用，数值拟合数学模型法是应用最多的方法，主要分为三种：曲线拟合、平面拟合、曲面拟合，从通用性、实用性及计算有效性方面看主要有：多项式曲面拟合、等值线绘图法、三次样条曲线拟合、平面拟合移动法曲面拟合、多面函数曲面拟合、样条函数曲面拟合。

（一）等值线图示法

等值线图示法是对于平坦地区最常用最直接的方法，也是最早的GPS水准方法，这种方法的主要思想是内插，绘制出高程异常的等值线图，利用内插法来确定未知点的高程异常值，其具体做法是：在所测区域均匀的布设GPS水准点，通过观测来确定大地高，已知正常高，利用相关公式来确定已知点的高程异常值，通过选择合适的比例尺，按照已知点的坐标将点绘制在图纸内，将已知点的高程异常值标注出来，然后确定出合适的等高距（通常用1～5cm），绘制出高程异常值的等值线图，之后通过待定點的坐标，在图上确定出点位，之后就可以利用内插的方法确定出待定点的高程异常值，进而求得该点的正常高。这种方法的优点是方便、简捷，其精度可以达到厘米级别，但是高程异常值经常受到等值线绘制精度和内插误差的影响。

（二）多项式曲线拟合

对于线状拟合主要应用的方法是多项式曲线拟合法，其主要思想是在所测区域内建立一个与该区域内似大地水准面最为接近的数学模型，这种方法所计算出来得高程异常值精度取决于该数学模型与区域内的似大地水准面接近程度。

此种拟合方法适用于测区范围较小，路线不能太长，并且控制点和测点距离不能太远，一般情况下应该严格限制在300m以内才能够保证该方法的精度不受影响，理论上多项式的次数可以是二次、三次甚至N次，对于二次多项式只需要6个重合点数据就可以在区域内进行拟合，对于三次多项式拟合就需要10个重合点数据，考虑到简单方便的原则，一般用二三次多项式拟合进行区域线性拟合，但是随着次数的增高，模拟曲线出现震荡现象，和实际的高程异常相差较大这样的话就会在一定程度上影响拟合精度。

（三）多项式曲面拟合

多项式曲面拟合是曲面拟合中的一种常用的方法，它的主要思想：已知测区内的若干个已知水准点，并且用GPS测量得到已知点的大地高值，利用这些已知值把该区域内的似大地水准面利用数学曲面近似的拟合。在该测区内建立与该区域内似大地水准面最接近的数学模型，然后利用高程拟合的模型求出该区域内未知点位的高程信息。

多项式函数理论上可以任意确定次数，但是通过大量的研究发现，次数不断增高的情况下，在曲面拟合模拟的过程中震荡就会越明显产生一定的误差，从而导致高程异常曲面的模拟结果误差较大，同时考虑到次数越高对已知点个数的要求也会越高，三次多项式拟合时需要最少十个已知点数据，而二次多项式拟合至少需要六个已知点数据就可以进行曲面的拟合，因此在曲面拟合的过程中建议使用二次多项式进行拟合。

五、结语

GPS技术很大程度上促进了测绘行业的发展，本文分别对三种常用的高程拟合方法的适用条件进行了分析并得出结论，以便在实际生产中选择合适的拟合方法进行拟合得到更精确的高程数据。

参考文献：

[1]潘正风，程效军，成枢，王腾军，宋伟东，邹进贵.数字测图原理与方法[M].武汉大学出版社，2011.

[2]胡良柏.GPS高程拟合的研究[D].江西理工大学，2008.

[3]马玉晓，潘传姣.GPS高程最佳拟合技术的实现[C].2004.

[4]陈俊勇.我国GPS水准网的布设及其精度探讨[J].测绘学报，1993（02）.

[5]张冰，马开锋，陈南祥.GPS高程拟合模型研究[J].华北水利水电学院学报，2008（02）.

（作者单位：新疆工程学院）