东北水稻叶片SPAD遥感光谱估算模型

张新乐 于滋洋 李厚萱 刘焕军* 张忠臣 赵明明 王 翔

(1.东北农业大学 资源与环境学院，哈尔滨 150030； 2.东北农业大学 农学院，哈尔滨 150030)

叶绿素含量是作物生长的重要指标，是评价作物光合作用能力，监测作物生长状况，判断作物生理营养好坏的重要依据，因此可以通过监测作物叶绿素含量间接对作物生长条件进行调控。目前，传统的叶绿素含量检测方法有分光分度计法、荧光分析法及活体叶绿素仪法等[1]，但这些方法操作复杂繁琐，并会破坏植物生长，因此迫切需要寻找高效和非破坏性的叶绿素检测方法。

遥感技术可以为作物生理指标的定量化监测提供一种简便有效且非破坏性的采集方法[2]。国内外许多学者在监测植被生理指标方面做了大量研究[3-5]。张春兰等[6]在优选光谱指数和确定最佳自变量个数的基础上结合随机森林算法构建了LAI反演模型；Inoue等[7]在水稻关键时期利用高光谱数据确定作物冠层含氮量估算的敏感波段对其进行估算；梁亮等[8]利用导数光谱构建了新型光谱指数进行小麦含水量反演并进行含水量遥感制图；利用遥感数据同样可以对作物进行产量估测[9-11]。同样针对于叶绿素反演的研究也有很多，有学者提出一种估算作物叶片叶绿素含量和冠层叶绿素含量反演方法并建立混合反演模型[12]；贺英等[13]利用数码相机影像采用可见光波段构建SPAD估算模型；陈志强等[14]通过对比分析不同年间光谱指数与SPAD的关系，确立能良好估测整个生育期玉米叶片SPAD的光谱指数；以红边参数为自变量同样可以对SPAD进行良好的估测，并且相对于红边位置以红边峰度为自变量可以提高估算精度[15]。Gitelson等[16]表明基于叶片尺度估算叶绿素适宜指数。传统的回归模型对反演的精度有一定的限制，由于植被生理参数与植被光谱反射率关系是非线性的，人工神经网络具有非线性和适应性的特点，在解决非线性拟合问题方面有很大优势[17]。并且与主成分回归和偏最小二乘回归等模型相比，BP神经网络模型预测精度更高[18]。因此，BP神经网络与高光谱遥感反演的结合对植被生理参数进行反演可以提高反演精度。利用神经网络模型反演精度明显高于多元回归模型[19]；采用不同植被指数作为 BP神经网络模型的输入量能较好地反演不同地区不同作物的生理参数[20-22]。

以上基于BP神经网络反演的研究均直接采用植被指数作为输入量，缺乏对不同输入因子的对比分析及优势探讨。因此本研究采用东北地区不同品种水稻作为研究对象，探究高光谱监测水稻叶片SPAD的敏感波段和最优指数，建立相应的SPAD估算回归模型,旨在确定适宜东北地区水稻叶片SPAD估算的最优输入量及最优算法。

1 材料与方法

1.1 试验设计

水稻样本采集于2017年6—9月的黑龙江省哈尔滨市呼兰区试验田(45.9°N，126.8°E)为晚熟品种188和早熟品种龙稻11号2种。数据获取时期包括移栽后、分蘖期、拔节期、孕穗期和抽穗期5个关键时期。施肥处理采用移栽施一次基肥，分蘖期和抽穗期之前进行2次追肥的施肥方式。基肥、分蘖肥和穗肥施肥比例为5∶2∶3，氮磷钾比例为2∶1∶2。总共设置6个小区，氮肥处理设置0、90.0、112.5、135.0、157.5和180.0 kg/hm26个肥力水平，分别用N1、N2、N3、N4、N5和N6表示。施肥品种分别为二铵、尿素和硫酸钾，肥中各营养素含量分别为二铵的含磷量为46%，含氮量为17%；尿素的含氮量为46%；硫酸钾的含钾量为50%。每个施肥水平设置4次重复，随机区组排列，小区面积为72 m2。5月24日播种，其他管理同常规高产田。

1.2 数据采集与处理

水稻叶片反射光谱数据采用美国SVC HR768i型光谱辐射仪，光谱探测范围350～2 500 nm，光谱分辨率为3.5、8.5和6.5 nm。利用自带光源型手持叶片光谱探测器直接测定叶片光谱，光源为内置卤素灯。测定前，利用漫反射参考板进行仪器校正。每个肥力水平在长势均一处选择6组叶片进行光谱反射率测定，对每个小区选择的样本点分别采集光谱曲线。测定前对测定的叶片进行标识，注明编号。对得到的光谱反射率利用SVC HR-768 PC进行平滑处理，去除不同采样间隔连接处的拐点噪声。6组叶片光谱反射率数据取算数平均值得到叶片的最终光谱反射率。本研究将原始反射率重采样至1 nm。

采用SPAD-502型手持式叶绿素仪同步测定水稻叶片的SPAD值。测量时，在每片叶子上均匀测取2个SPAD值，取算数平均值为最终的SPAD值；取6组数据算数平均值为最终的叶片SPAD值。共得到120个样本数据，随机抽取80个作为建模样本，剩余40个作为验证样本。

1.3 特征参数选择

光谱特征参数分别为蓝黄红三边及绿峰红谷处位置形状参数、绿峰与红谷的比值、红边面积与蓝边面积和黄边面积的比值和归一化值(表1)。所有植被指数均在重采样1 nm基础上计算任意2个波段的原始反射率和一阶导数值组合而成的所有差值、比值和归一化值，并分析其与水稻叶片SPAD的关系，进行最优化筛选得到最优波段组合。利用Python编程实现波段组合与最优值筛选。

表1 光谱指数计算公式Table 1 Calculation formula of spectral index

1.4 模型构建与精度验证

采用BP神经网络，网络共有输入层、隐藏层和输出层3层。隐藏层函数为‘tansig’，输出层函数为‘purelin’，训练函数为‘trainlm’。隐含层节点数q则根据式(1)给定的范围，最终确定为4～10。

(1)

式中：k为输入层单元数；m为输出层单元数；α为1～10的常数。

共获得120组有效数据，将其中80组作为训练样本，40组作为验证样本，以决定系数(R2)、均方根误差(RMSE)作为指标评价指标。R2越大，RMSE越小，模型越稳定。式(2)为均方根误差的计算公式。

(2)

2 结果与分析

2.1 叶片反射光谱特征分析

叶片反射率主要受叶片内色素、细胞结构及叶片含水量三方面影响。在可见光波段(350～720 nm)叶片反射率主要受叶片内色素影响，其中叶片反射率受叶绿素影响最大。随水稻植株生长，水稻叶片光合能力增强和对红光、蓝光吸收增强，导致红蓝波段反射率逐渐减小。在450和670 nm附近水稻叶片反射率形成2个吸收谷。在红波段与蓝波段处的强吸收使绿波段反射率逐渐突出，水稻植株叶片颜色逐渐变绿，在绿波段处形成反射峰。本试验两品种水稻绿波段反射峰均在分蘖期达到峰值。在近红外波段(720～1 300 nm)，水稻光谱曲线特征受叶片内部细胞结构的影响，由于水稻叶片的细胞壁和细胞空隙间折射率影响，导致近红外波段处水稻叶片光谱反射率较高。品种188在近红外波段处移栽后与分蘖期反射率相差较大，在分蘖期以后近红外处反射率增加幅度变小，由于188为晚熟品种所以水稻反射率在水稻生长末期依然呈增长趋势。龙稻11在近红外波段处移栽后与分蘖期反射率相差不大，水稻反射率在近红外处增长较为稳定，由于龙稻11号为早熟品种导致其在拔节孕穗之后近红外波段处反射率增长幅度不显著，在抽穗期反射率略有下降。在短波红外内(1 300～2 500 nm)，水稻光谱反射率主要受叶片含水量影响，其中在1 400和1 900 nm处为2个水分吸收带，在1 600和2 200 nm处则是位于水分吸收带之间形成的反射峰(图1)。

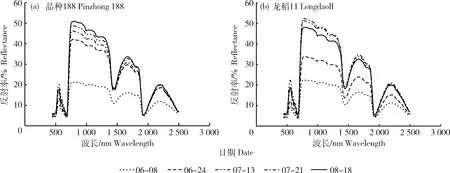
图1 品种188和龙稻11在N3施肥处理下不同时期叶片反射率曲线
Fig.1 Leaf reflectance curves of variety 188 and Longdao 11 under N3 fertilization at different stages

2.2 相关性分析

2.2.1反射率各波段相关性分析

由图2可以看出，光谱反射率与水稻SPAD值在400～1 000 nm存在正相关关系，在可见光范围内，光谱反射率与水稻SPAD值相关系数逐渐减小并在640 nm处相关系数达到最低；光谱反射率与水稻SAPD相关系数在红边(690～760 nm)范围内逐渐变大，在近红外范围内相关系数达到最大并且相关系数值保持稳定，最大相关系数在反射率为982 nm处，达到0.68。

在400～1 000 nm波长，一阶微分光谱具有两峰一谷的特征：左峰位于波长480～550 nm，峰顶部位于520 nm处，振幅较小，约为右峰的1/3；右峰位于波长670～780 nm，峰顶部位于700 nm处。左峰波长范围正好处在蓝边(490～530 nm)范围，右峰波长范围正好处在红边(680～760 nm)范围；577 nm处有明显的波谷。400～688 nm和750～1 000 nm一阶微分光谱与水稻SPAD值相关关系波动较大并且都以0为中心上下波动；690～770 nm一阶微分光谱与水稻SPAD值相关性达到极显著正相关,最大相关系数可达0.78。

图2 SPAD与光谱反射率、一阶微分相关分析
Fig.2 Correlation coefficients between SPAD and Spectral reflectance, First derivative

2.2.2红边参数与植被指数相关性分析

在基于高光谱位置和面积的参数与SPAD的相关分析中可以发现，除蓝边位置，黄边位置和红谷位置外，其余参数均与SPAD呈极显著相关关系。其中红边位置和红边面积与SPAD相关系数明显大于其他光谱参数，相关系数在0.6以上(表2)。绿峰处参数与SPAD相关性极显著，但是相关系数较小在0.27左右。黄边幅值与黄边面积与SPAD呈极显著负相关。

在植被指数与SPAD相关性分析中可以发现，三类植被指数均与SPAD极显著相关且相关系数均在0.8以上。两波段原始反射率和一阶微分光谱归一化指数形式与SPAD相关性显著高于差值和比值2种形式，并且基于一阶导数构建的植被指数相关系数整体高于原始反射率所构建的植被指数。本研究筛选出相关系数绝对值>0.8的参数作为估算模型的自变量，所选自变量为本所构建的6种植被指数。

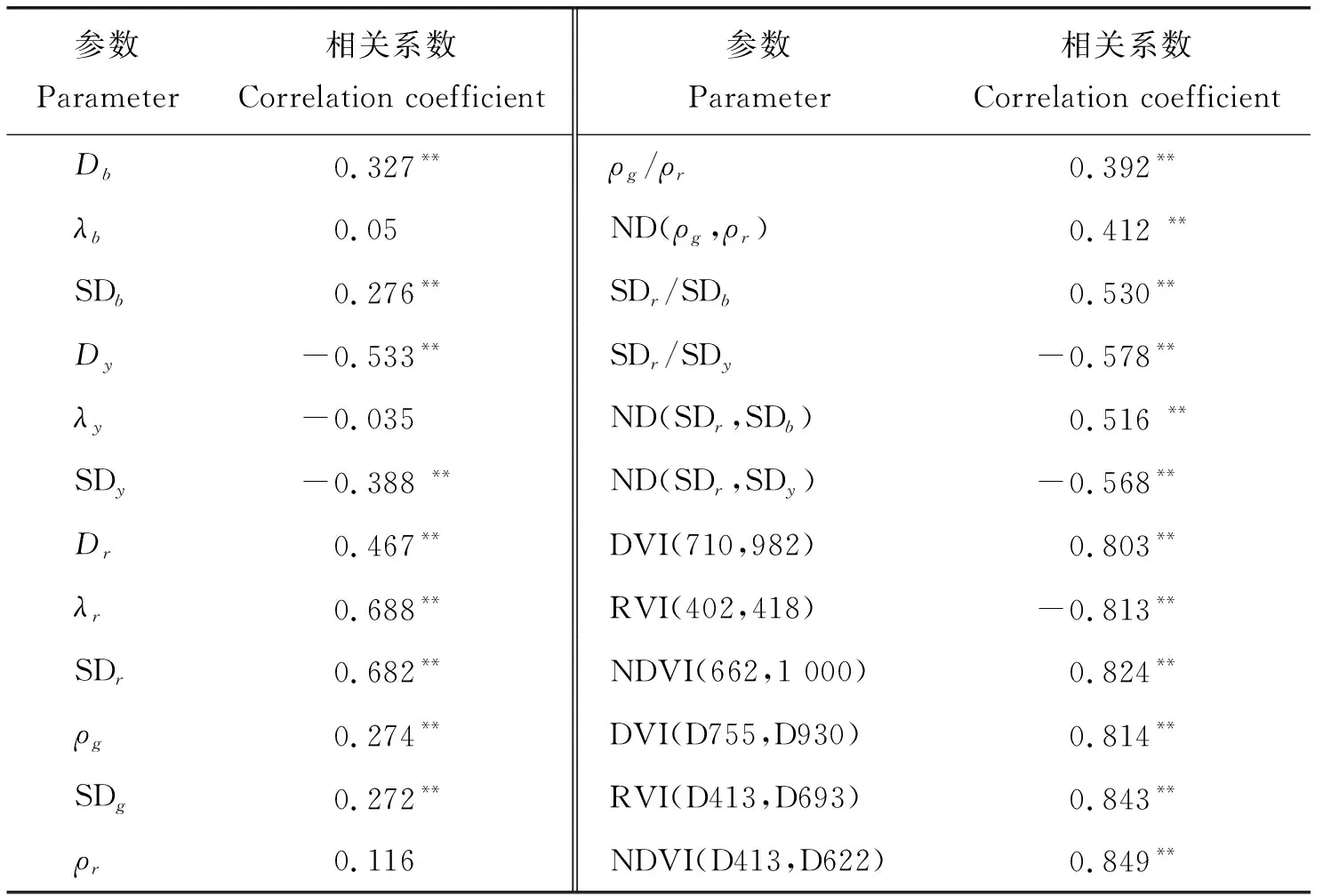
表2 光谱参数、植被指数与SPAD的相关系数Table 2 Correlation coefficient between spectral parameters, vegetation index and SPAD

注：**表示在0.01水平差异显著。

Note：** shows significant correlation at the level of 0.01.

3 SPAD高光谱预测模型

3.1 基于一阶微分单一波段的SPAD估算模型

因为一阶微分值与SPAD具有最大相关系数在波长为729 nm处，所以以729 nm处一阶微分值为输入量构建SPAD回归模型。表3为729 nm处一阶微分光谱与水稻叶片SPAD值的估算回归模型。通过比较发现，对数、多项式和幂函数的建模的决定系数R2均>0.6，并且3种模型的验证模型决定系数R2均>0.7。由验证样本分析，对数模型和多项式模型R2高于其他类回归模型， RMSE小于其他类回归模型，因此对数模型和多项式模型为最佳估算模型。幂函数模型估算效果相对较好。但是验证样本决定系数R2明显大于建模样本，并且差值接近1。验证样本均方根误差也明显大于建模样本。

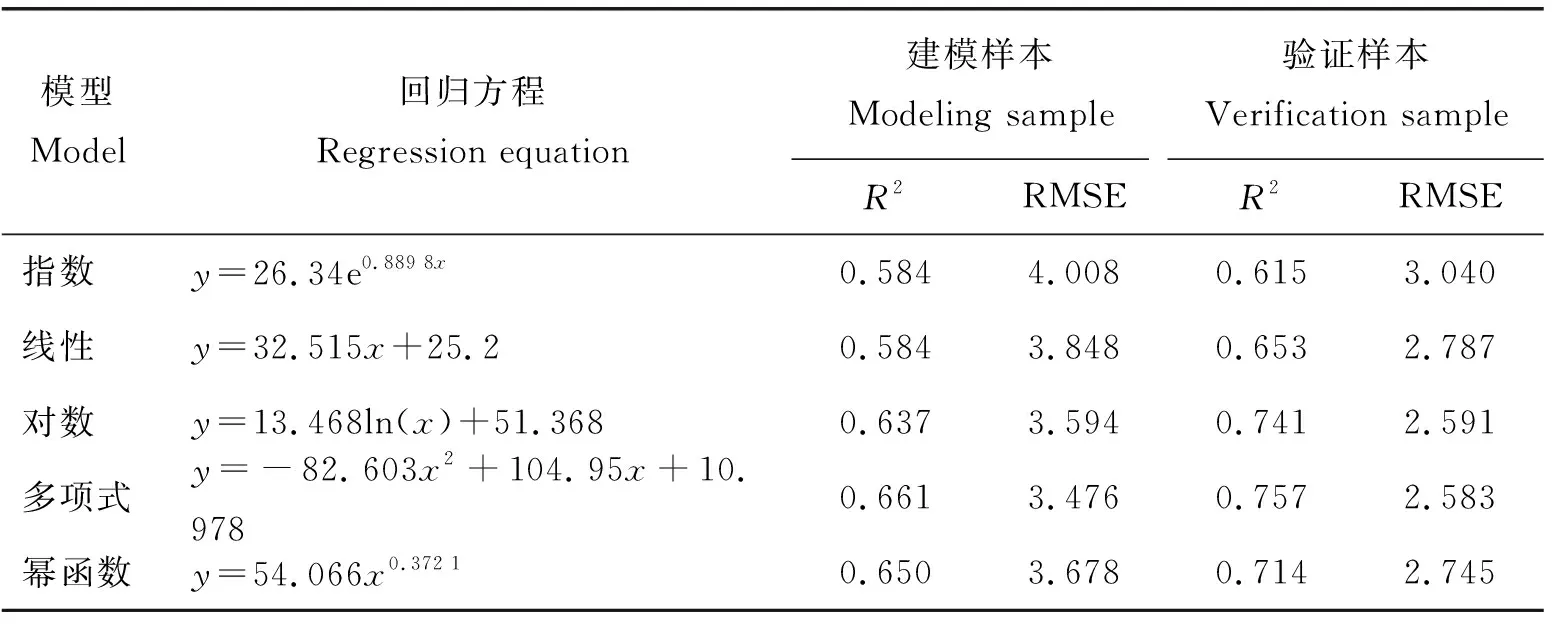
表3 一阶微分SPAD值估算回归模型Table 3 First order differential SPAD estimation regression model

3.2 基于植被指数的SPAD估算模型

在光谱参数、植被指数与SPAD的相关分析中发现，选取的植被指数相关系数大于所有光谱参数，并且相关系数在0.8以上(表2)。因此采用指数、一元线性、对数、多项式和幂函数构建基于植被指数回归方程，将每种植被指数精度最高的方程作为估算结果。表4为以植被指数为输入量的水稻SPAD最优估算模型，验证样本中，以DVI(710,982)、DVI(D755，D930) 和NDVI(662,1 000)为输入量的回归模型决定系数都在0.7以上。可以发现以两波段原始反射率或一阶微分光谱差值指数形式组合计算的DVI为自变量，所建立的回归模型精度高于比值和归一化值2种形式，其中以DVI(D755，D930)为自变量建立的回归模型精度验证样本R2为0.785，RMSE为2.184，此模型为最佳估算模型；NDVI(662,1 000)为自变量的回归模型R2为0.74，RMSE为2.575，估算精度同样较好。

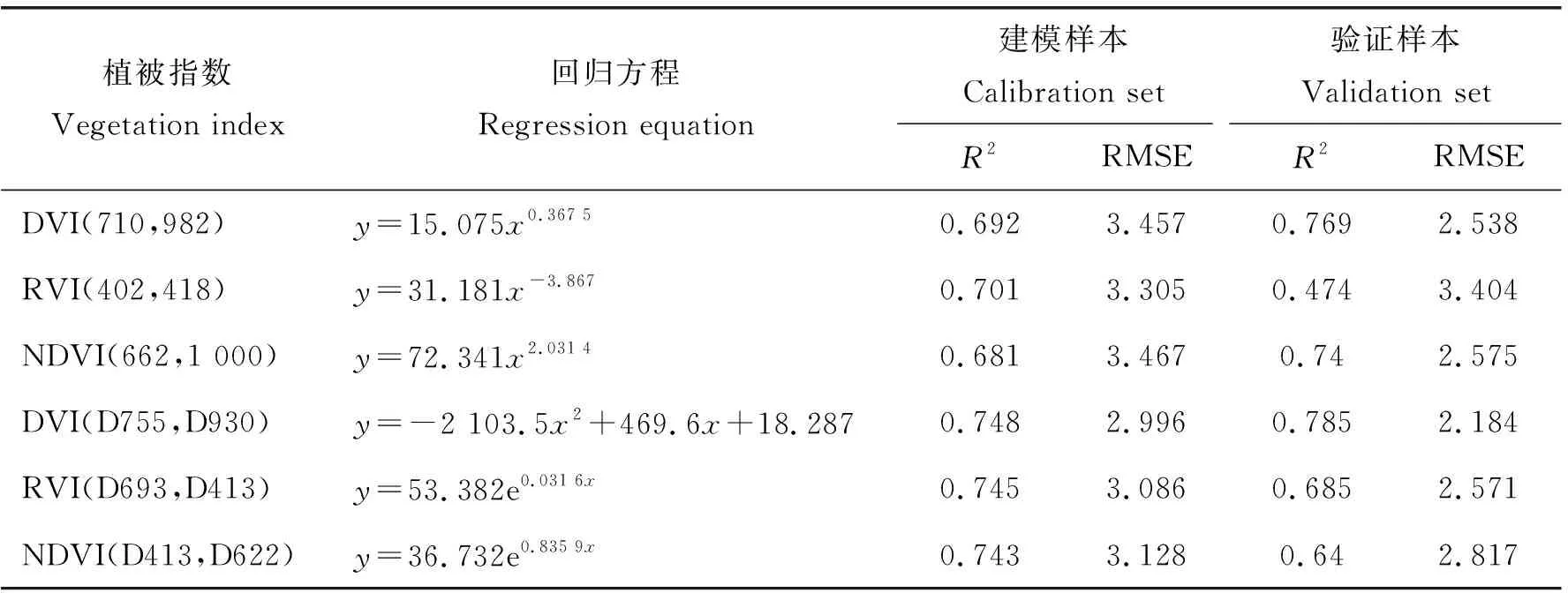
表4 植被指数与SPAD值估算回归模型Table 4 Regression model of vegetation index and SPAD estimation

3.3 水稻叶片SPAD神经网络模型

所选取输入层共有3组数据，分别为构建回归模型所选取的四组植被指数NDVI(662,1 000)、DVI(D755，D930)、RVI(D693，D413)和NDVI(D413，D622)；蓝波段(500 nm)、绿波段(550 nm)、红波段(660 nm)和近红外波段(860 nm)处反射率，波段选择主要以植被在可见光-近红外光谱反射特征差异为原则，利用人工神经网络模拟可以寻求不同波段做的互补优势[23]；选取450、540、680和 960 nm 处反射率与第二组数据对比，其中所选波段均在可见光与近红外范围与SPAD相关系数较高。将水稻叶片实测SPAD值1个变量作为输出层。

表5为不同输入层及不同隐含层节点数的水稻叶片SPAD值神经网络模拟的建模与验证结果。由表5可知，采用500、550、660和860 nm作为输入量，隐含层节点数为10的条件下估算精度最高。通过分析可以发现，当植被指数作为输入量，隐含层节点数为7时，神经网络模型相较于传统回归模型精度提高。在隐含层节点数为7～10时模型趋于稳定，R2稳定在0.8以上；当采用500、550、660和 860 nm 波段反射率作为输入量时，隐含层节点数为7，相比于以植被指数作为输入层模型精度提高，在隐含层节点数为8～10时，模型精度趋于稳定；当采用450、540、680和960 nm反射率作为输入量时，隐含层节点数在8以上时，模型精度同样趋于稳定。第三组输入量同第二组输入量相比，模型精度差异很小。说明以神经网络模型为基础，以不同波段反射率作为输入量可以对水稻叶片SPAD值进行估算。

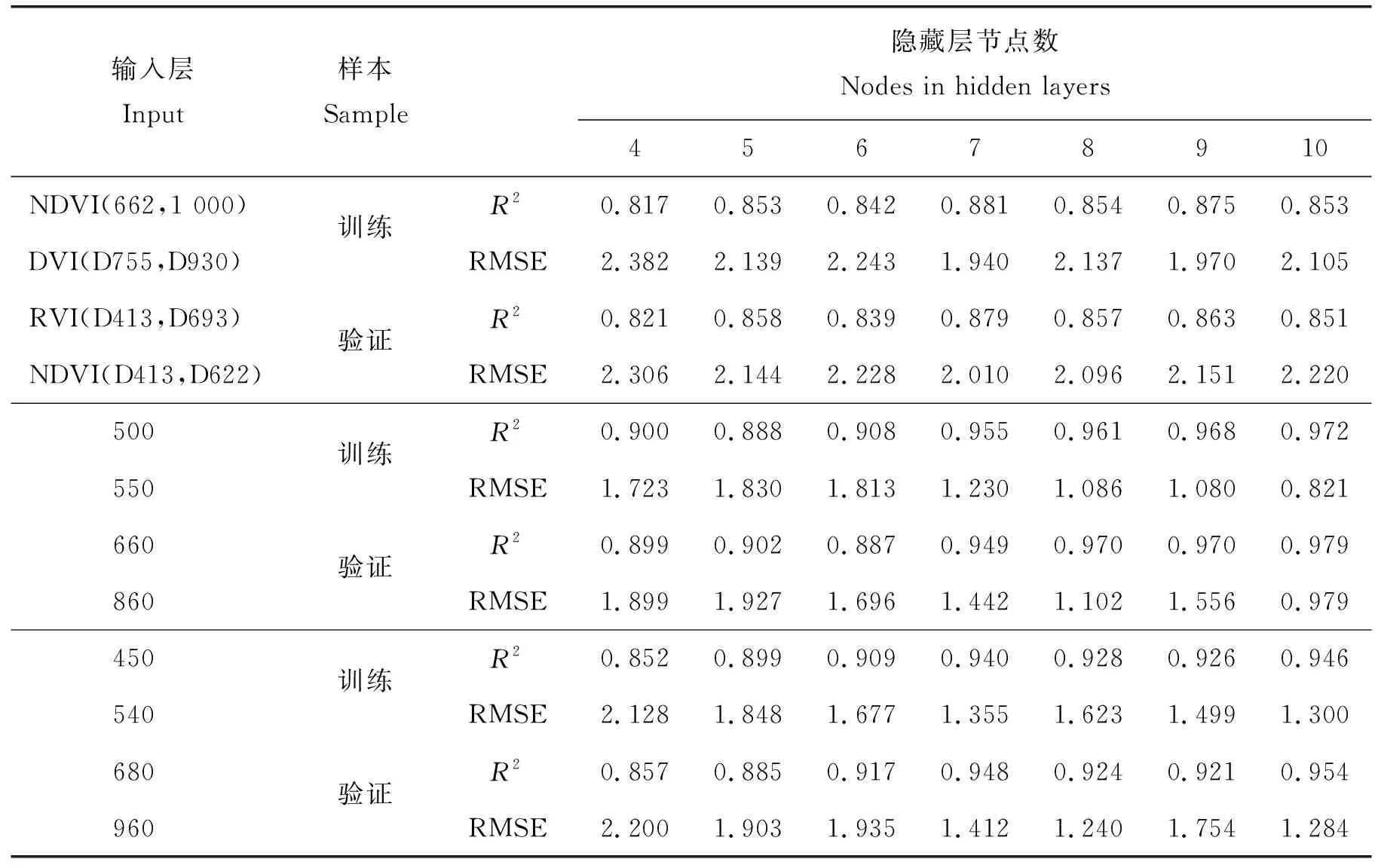
表5 水稻叶片光谱SPAD神经网络模拟建模与验证结果Table 5 Modeling and validation of rice leaf spectral SPAD neural network

4 讨 论

本研究首先分析了不同品种水稻不同生育期在光谱特征上的特点，不同品种在不同生育期反射光谱形状大致相似，之前也有类似的结果[24]。在建立估算模型时选择三类变量与水稻叶片SPAD进行相关性分析，包括1)原始反射率和一阶微分光谱；2)基于原始反射率及一阶微分构建的光谱参数；3)基于原始反射率及一阶微分进行优选计算的植被指数。在相关性分析中发现， 一阶微分光谱与SPAD相关性好于原始反射率，以往有研究证明微分光谱与植被生理参数相关性更好[25]，并且植被指数与SPAD相关性好于光谱参数。

3种植被指数中归一化指数形式的组合相关性高于其他2种形式，但是建模估算结果表明，以差值形式作为自变量估算精度最高。精度最高的3个建模自变量分别为DVI(710,982)、DVI(D755,D930)和NDVI(622,1 000)，这3种指数的波段组合都是红波段、红边处与近红外波段的组合，说明红波段与近红外波段是估算SPAD的最优组合。并且不同建模方法估算精度差异较大。基于单波段一阶微分和植被指数建立估算回归模型中非线性模型估算精度明显高于线性模型，原因可能有2个：1)在植被生长过程中叶绿素在不同阶段变化速率不同，导致在生长末期叶绿素含量存在饱和现象；2)在光谱采集和SPAD值数据采集过程中由于操作原因导致估算结果呈明显的非线性关系。回归模型中验证样本精度明显高于建模样本，说明估算的经验模型不稳定，模型的普适性需要加强。

本研究中采用BP神经网络可以提高估算的精度，与传统回归模型相比预测效果更好，这与前人研究的结果一致[26]。但以上研究直接将植被指数作为输入量，缺乏对最优输入因子的优化筛选。采用50、550、660和860 nm作为输入量比采用植被指数作为输入量估算精度高，这是因为植被指数之间相关性较高，神经网络所能提取的有用信息较少，而以可见光和近红外波段处反射率作为输入量可以实现不同波段反射率间信息的互补，以此提高估算精度；采用450、540、680和960 nm波段的反射率作为输入量对比发现，采用不同波段反射率作为输入量对估算精度影响较小，因为BP神经网络具有强大的自学习能力且能有效解决非线性问题，可以通过不同波段作为输入量。但是波段选择也不是完全随机的，本研究是在与叶绿素相关性较高的可见光和近红外波段处的反射率进行分析，其他波段处的反射率作为输入量还有待探究。BP神经网络虽然预测效果较好，但也存在一些不足，样本数量要足够大，否则模型训练结果有很大随机性。本研究尚存在部分局限性，由于使用一年一个区的样本数据，缺乏对不同年份不同地区模型适宜性的探讨，因此今后需要针对更多水稻品种在不同年份及区域的适宜模型做进一步的探究。

5 结 论

本研究针对东北地区5个时期不同品种水稻叶片进行实验，建立水稻叶片SPAD估算的回归模型和BP神经网络模型，比较2种模型精度并且比较在不同参数作为输入量的情况下BP神经网络模型的精度，可以得出以下结论：

1)不同品种水稻光谱反射率形状大致相似，早熟品种水稻近红外处反射率在孕穗期达到饱和并且稳定，孕穗期和抽穗期反射率差异较小；晚熟品种水稻近红外处反射率在孕穗期仍然小于抽穗期。两品种水稻绿峰处反射率均在分蘖期达到峰值。

2)水稻叶片一阶微分值与SPAD值在红边范围内720～755 nm相关系数达到最大，在732 nm处具有最大相关系数0.78， 利用此波段处的一阶微分值构建的对数和多项式模型为最佳估算模型。在其他波段一阶微分光谱与SPAD相关系数波动较大。

3)在光谱特征参数与SPAD相关分析中，红边位置和红边面积与SPAD相关系数最大。在植被指数中，两波段归一化值组合与水稻叶片SPAD相关性较好，但是差值组合建立回归模型精度最高。在回归模型中以植被指数DVI(D755，D930)为自变量建立的多项式模型为最佳估算模型，估算模型与南方水稻SPAD估算模型有所不同。

4)BP神经网络模型在隐藏节点数为7时估算精度达到稳定，并且利用BP神经网络模型可以提高反演精度，采用波段反射率作为输入量精度明显高于采用植被指数作为输入量，并且在可见光和近红外处经过不同波段反射率的尝试说明神经网络模型较为稳定，可以用来反演叶绿素相对含量。