一种改进的海底控制点非差定位函数模型

马越原，曾安敏，许扬胤

（1.信息工程大学，河南 郑州 450001；2.西安测绘研究所，陕西 西安 710054）

海洋定位、导航和授时（PNT）是海上运输、海洋环境保护、海洋权益维护和海上安全保障的重要基础。通常单一的导航定位方法不足以支持水下长时间的导航定位。多传感器综合定位有助于开展一系列海洋活动[1-3]。在海面航行的船只可以采用类似陆地和空中的导航技术进行导航定位。北斗导航定位系统（BDS）由于其短消息通信和位置跟踪等特色功能[4-5]，对海洋用户有着很大的帮助，但是对水下导航和定位没有任何帮助。由于电磁波无法在海水中远距离传播，水下航行器通常使用惯性导航系统（INS）、声学传感器、几何或者物理匹配等方法进行导航[6-7]。然而，海底定位除了利用海面GNSS定位的支撑下进行声学定位以外，没有其他更好的方法。

由于海洋环境复杂，大多数水下定位方法都存在时变误差和累计误差。本文主要研究水下定位的函数模型优化问题。在测量过程中，系统误差总是无法避免的，系统误差通常是通过外部标定来修正或者通过函数模型来补偿。同时，测量策略和测量组合方法也是减少系统误差影响的有效方法[8-9]。本文将描述常用的传统水下非差定位模型，详细介绍定位流程，并分析传统定位模型所存在的弊端。

1 传统水下非差定位函数模型

在进行海底大地测量控制点的声学定位时，通常采用测量船走航的方式进行，通过安装在测量船底的声学换能器在不同时刻不同位置向搭载有水声应答器的海底控制点发射声脉冲信号，应答器接收该信号后立刻返回一个应答声脉冲信号，声学换能器接收并记录发射信号和接收信号的时间间隔t；利用船载GNSS接收机获取不同时刻测量船位置，这样就可以通过船体姿态角、GNSS接收机与声学换能器之间的偏移参数旋转归化得到声学换能器的位置。根据上述观测量我们就可以组成非差定位模型从而求解海底应答器的位置。

测量船在每个历元ti时刻的位置坐标为Pi(xi,yi,zi)，该位置是GNSS天线相位中心在WGS-84坐标系下的坐标，而偏移参数是在船体坐标系下测量所得到的，因此要计算出换能器的位置，需要进行坐标系转换。坐标系转换分为两步：（1）船体坐标系改正；（2）船体坐标系到WGS-84坐标系。转换矩阵为[10]：

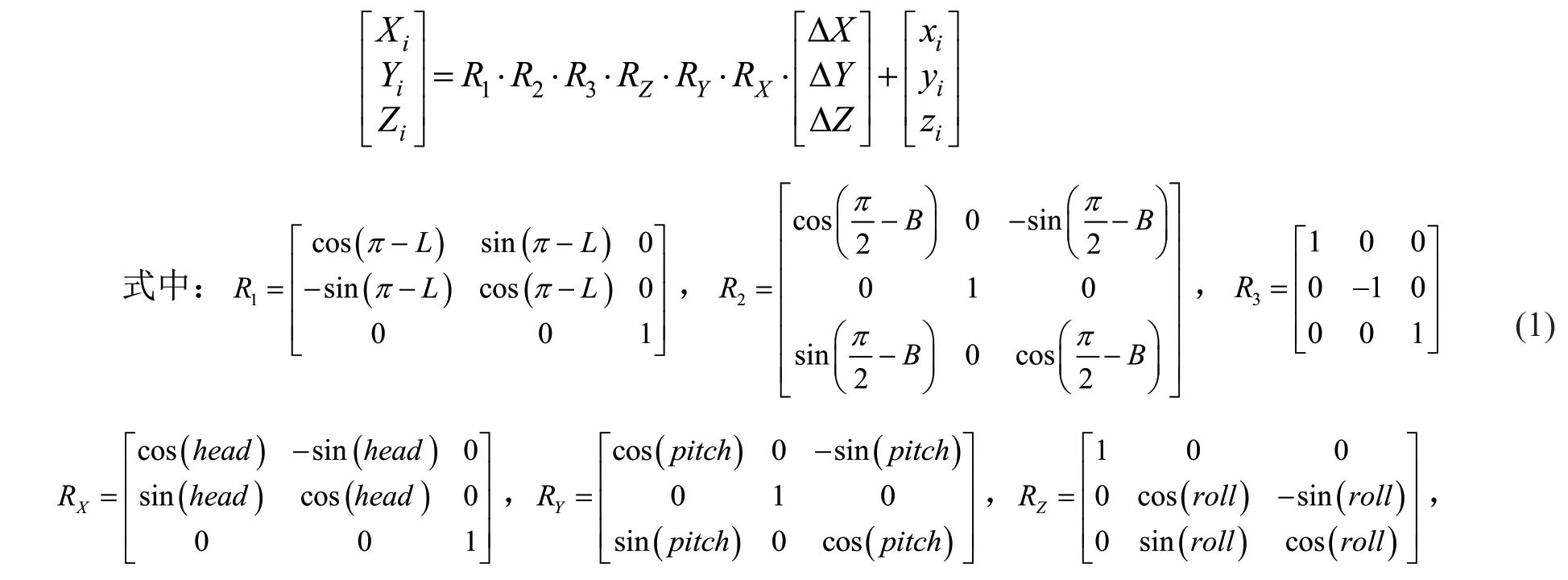
ΔX,ΔY,ΔZ为换能器与GNSS天线之间的偏移参数，Xi,Yi,Zi为换能器在WGS-84坐标系的坐标，L,B为经纬度，head为方位角、pitch为摇摆角、roll为横滚角。

将式（2）通过泰勒级数展开可得

将式（3）表示为矩阵形式，即

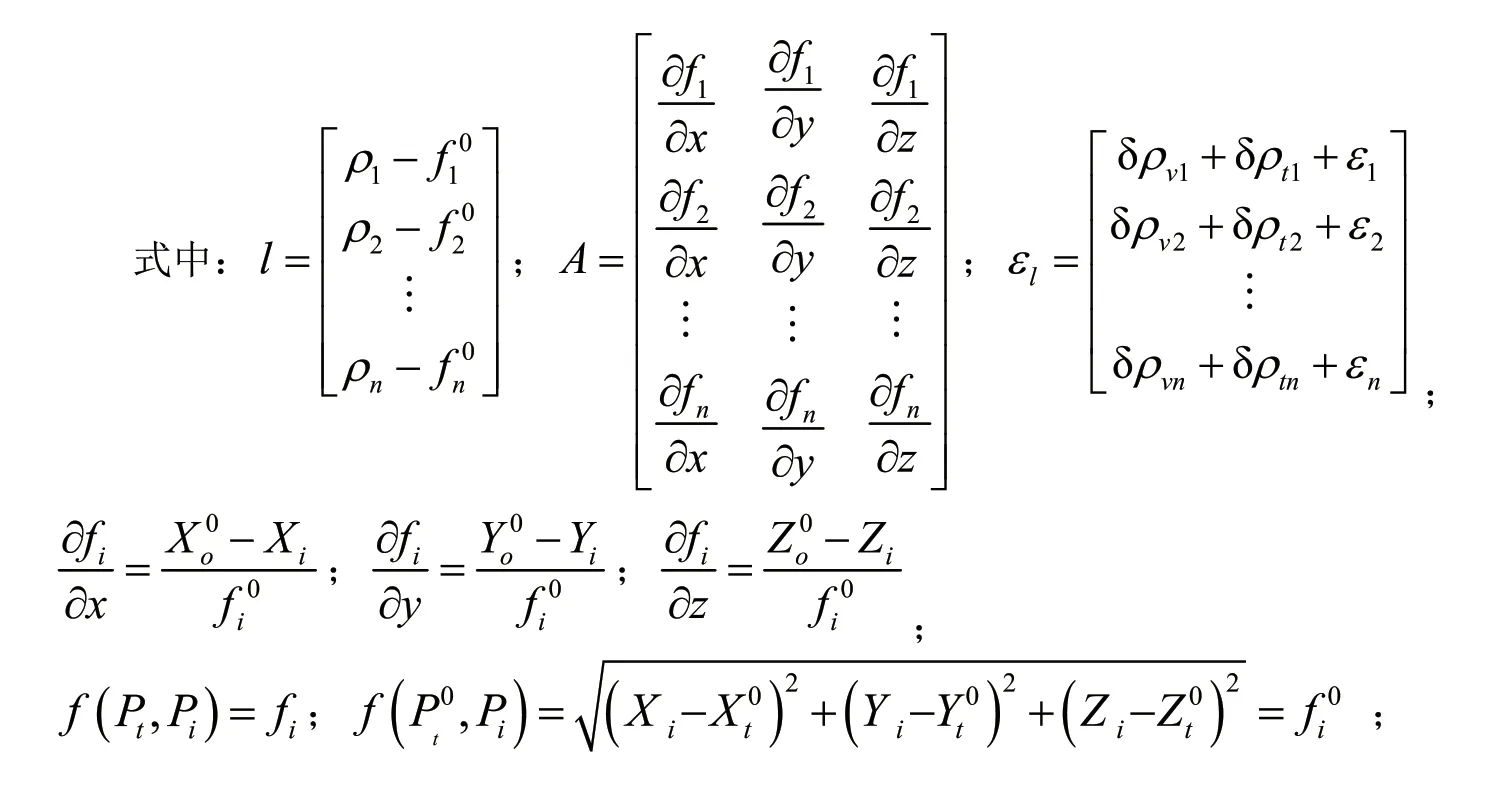
l为常数项；A为协方差矩阵；εl是误差项，包括声速误差和时延误差在内的随机误差和系统误差。

因此，在不考虑系统误差的情况下，误差方程可以写成

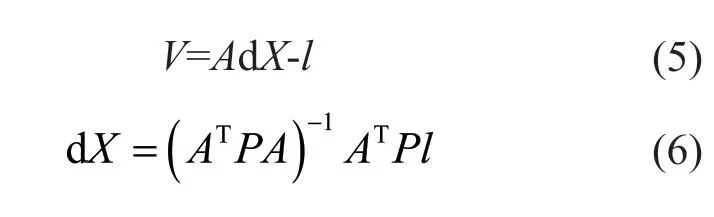
式中：V为观测值改正数矩阵；P为权矩阵。

上述定位函数模型称之为单程定位模型。

2 改进的水下非差定位函数模型

根据换能器和应答器的工作原理，换能器发出声脉冲信号，海底换能器接收后返回另一个声脉冲信号并由换能器接收，这个过程存在一个时间间隔t。在实际作业时，测量船是在匀速航行，在t时间内，测量船已经行进了一段距离。从传统水下非差定位模型的表达式中可以了解到，是假定测量船静止不动，从而认为换能器和应答器之间的距离为虽然测量船在作业时船速较慢，但是声脉冲信号在一去一回的这个过程中记录的时间t实际上是大于实际传播时间的，尤其是在深海作业时，误差尤为明显。因此，本文提出一种改进的水下非差定位模型，来解决上述问题给定位带来的影响。

假设在换能器发射声脉冲信号时刻t发射换能器的位置坐标为P发射（X1i,Y1i,Z1i），在换能器接收声脉冲信号时刻t接收换能器的位置坐标为P接收（X2i,Y2i,Z2i）。取海底应答器的初始位置为声脉冲信号的传播时间为t，则表达式为：

式中：ρ1+ρ2=ct，δρvi表示声速造成的测距误差；δρti表示时间延迟造成的测距误差；εi表示随机误差。

同式（2），将式（7）线性化可得表达式如下：

l为常数项；A为协方差矩阵；εl是误差项，包括声速误差和时延误差在内的随机误差和系统误差。

同理，在不考虑系统误差的情况下，误差方程可以写成

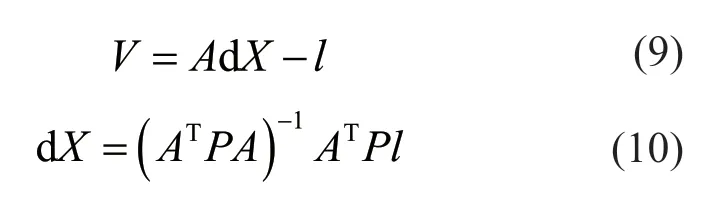
式中：V为观测值改正数矩阵；P为权矩阵。

上述定位函数模型，称之为双程定位模型。

3 实测算例分析

为检验分析双程定位函数模型的有效性，采用一次深海实验数据进行算例分析。实验海域平均水深约为3 000 m，该海域水下地形平坦。实验过程中，在海底布设一个水声应答器作为待测的海底控制点，测量船船速约为4 nmile/h，以海底控制点为中心进行了3种不同方式的走航：（1）以海底控制点为圆心，0.5倍水深为半径，称为小圆走航，共获得了684个声学时延数据；（2）以海底控制点为圆心，1.5倍水深为半径，称为大圆走航，共获得了1 122个声学时延数据；（3）以过顶控制点的方式线性走航，共获得了1 886个声学时延数据。

由于声速往往具有很强的不确定性和时空变化的特性，是水声定位的主要误差，因此声速的选取会对定位结果产生较大的影响。由于本文主要探讨双程模型较单程模型对定位的影响，故数据解算时假设声速就是该海域的平均声速，取1 500 m/s。所以在接下来给出的定位结果中，包含有声速误差所带来的影响。

如图1所示，图1-a、图1-b和图1-c分别为3种走航方式的走航航迹。

图1 测量船走航航迹

传统定位模型和改进定位模型在不同航迹下对海底控制点的定位精度如表1和表2所示。

表1 传统模型定位精度/m

表2 改进模型定位精度/m

σx、σy、σz分别为x、y、z坐标的中误差。σ和RMS的计算公式为：

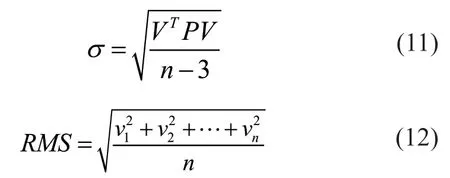
式中：v为残差值。

从表1和表2结果可以看出，不论是什么形状的走航航迹，改进函数模型的定位精度都较传统函数模型的定位精度有较大的提升，特别是水平方向的精度，提升尤为明显。

由于海洋环境复杂，海洋测量数据中常常含有大量的粗差，不仅影响定位精度，而且还可能受粗差的影响使得改进函数模型的定位精度不一定优于传统定位模型，从而使得单一的最小二乘定位解算算例不具有说服力。因此，在解算过程中，为了抑制异常误差的影响，均采用IGGIII方案抗差估计法进行解算，解算结果如表3和表4所示。

表3 传统模型抗差解算定位精度/m

表4 改进模型抗差解算定位精度/m

从表3和表4可以看出，经过抗差解算后，水平方向和垂直方向的定位精度进一步得到了提高，说明在抗差最小二乘的基础上，改进的定位函数模型能得到更好的计算效果。同时也可以说明，改进的定位函数模型确实优于传统定位函数模型，更符合海底定位过程的实际情况。

4 结论

本文介绍了传统水下非差定位函数模型的计算流程，分析了传统定位函数模型存在的弊端，并在此基础上提出了改进的水下非差定位函数模型，通过不同走航航迹获得的实测数据计算结果分析，对比两种函数模型的定位精度，得到以下结论：（1）双程模型定位模型较单程定位模型能准确描述测量船在测量时发射和接收声信号的实际情况，有效改正了由于声信号在传播过程中测量船继续行进所带来的时延测距误差，提高了海底控制点的定位精度；（2）针对海洋测量数据可能存在大量粗差的情况，采用抗差最小二乘定位解算能有效克服粗差对定位精度带来的影响；（3）测量船在线性走航时，改进函数模型更能有效消除测距误差对水平分量的影响，水平分量的精度可达毫米级；高程分量精度稍显逊色，精度为厘米级。