Logistic方程混沌周期点与精度研究
2020-03-16宋大华宋大全章慧鸣
宋大华 宋大全 章慧鸣


摘 要:Logistic方程存在不动点和短周期现象,为了研究Logistic方程在轨道中的特点,选取初始状态值为0.75进行迭代,方程在控制参数值等于4时,存在着不动点.本文对不动点附近的短周期轨道进行混沌周期研究,目标是揭示不动点与短周期之间的关系,通过研究不动点附近轨道的规律深入研究混沌轨道的特性.实验结果表明,在低精度时,初始状态值为0.75处存在着短周期现象;高精度迭代也存在短周期现象.
关键词:Logistic方程;不动点;短周期;精度
[中图分类号]TP399 [文献标志码]A
Abstract:Logistic equation has the phenomenon of the fixed point and the short period. In order to study the property of Logistic equation in trajectories the initial status value of 0.75 is selected for the iteration. When the value of the control parameter is equal 4 in Logistic equation, there is a fixed point. This paper introduces the research of chaotic period with short periodic orbits near the fixed point. The goal is to reveal the relationship between the fixed point and the short period. Regularity of the orbit near the fixed point makes a profound study on the property of chaotic trajectories. Experimental results show that there is the short period at the initial status value of 0.75 with low precision. Besides, the situation of the short period exists with high precision in Logistic equation.
Key words:logistic equation; fixed point; short period; precision
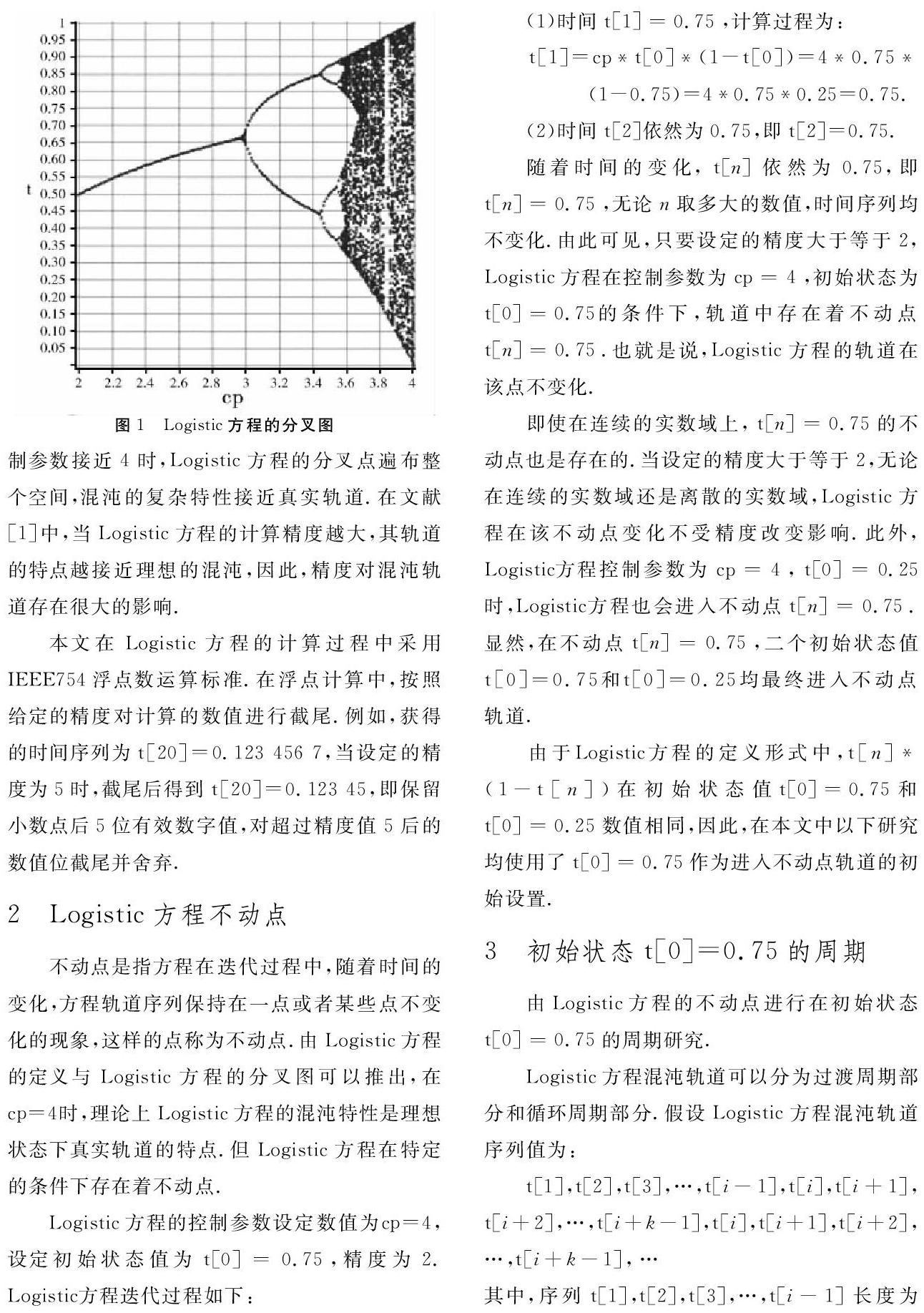
Logistic方程是典型的混沌動力学方程.在混沌动力学理论研究领域,当Logistic方程的轨道在连续的实数域中随着时间变化时,Logistic方程展现了自身复杂的变化,特别是其非周期、不可预测的以及具有良好的随机性特点.Logistic方程在连续实数域的真实轨道中所表现出的现象和特点被计算机模拟实现后,由于计算机中运算使用离散的数值表示轨道的变化,因此导致一些在真实轨道中的特性退化现象.
计算机中数值模拟的Logistic方程轨道存在二个部分,一部分是具有真实轨道特点的过渡轨道.随着计算机的有限计算精度的限制,最终Logistic方程的轨道在离散化的计算下进入循环轨道,在这个部分,轨道的变化出现有规律的重叠.现有的文献中,对于计算机模拟下轨道的研究从理论上还没有统一的结论——因为没有任何一台计算机能够提供无限的精度来模拟计算Logistic方程——所以,数值模拟计算的轨道的特点也难以真正接近真实轨道.典型的例证在文献[1]中已经进行了一些研究,理想的混沌轨道在离散的数值计算的计算机中受到精度的影响很大,目前还没有关于过渡轨道与循环轨道的深入研究,特别是过渡轨道和循环轨道哪一个更加能够表现轨道的特点.
Logistic方程在计算机领域被广泛用于随机数发生器中,例如产生随机数,生成哈希值等.Logistic方程也存在着不动点和短周期点的现象.由于不动点和短周期对于随机数发生器具有重要的影响,因此,对于不动点和短周期的研究是混沌随机数理论研究中重要的研究问题,也是混沌随机数应用的关键问题.有效地避免离散域中轨道的不动点和短周期,对于产生良好随机性混沌序列至关重要.从理论和实验的角度分析是对混沌随机数发生器的优劣进行评判的一种有效手段.本文主要研究Logistic方程轨道中的不动点以及在不动点附近的短周期现象.研究不动点附近的短周期现象是揭示短周期与不动点之间联系的一个有效途径,也是研究离散的数值模拟计算轨道中混沌方程特点的有效实验方法.本文的第一部分阐述Logistic方程的数学定义形式以及在计算机中模拟数值计算的时间序列模型方法.第二部分介绍Logistic方程不动点的基本研究方法和主要的不动点区域,分别从理论和实验方面进行阐述.第三部分介绍Logistic方程在初始状态0.75处的周期特点以及在该不动点附近的短周期现象.通过实验的方法与有限精度计算轨道的研究,揭示不动点附近轨道的特性,给出本文的结论与展望.
从实验结果可以看出,时间序列t[1]与t[9]出现相同值.同理,t[2]与t[10]也是相同值,因此,过渡周期长度为0,循环周期长度为8.
显然,提高计算精度来增加混沌周期的方法在一定的条件下是有效的,如果忽略了不动点,那么即使精度提高,也会存在短周期的现象.从现有的文献研究中,对不动点的研究报道不多,主要原因在于不动点在轨道中不易发现,而且短周期的轨道筛选需要极大的计算量,如果不采取并行计算和高性能计算机操作,犹如大海捞针.理论研究还难以建立坚实的推理基础,目前的实验方法受到有限精度的局限,因此,对于短周期和不动点的研究还需要不断的探索研究,发掘更好更快的方法,从理论上进行突破.
由于混沌方程的短周期现象不确定,也难以进行控制,因此,在利用混沌方程实现随机数发生器时,应尽量避免使用短周期区域的轨道序列.随着时间变化,大量的短周期序列将破坏混沌序列的随机性.
4 结论
Logistic方程存在着不动点和短周期的现象,特别是在初始状态t[0]=0.75处,当控制参数等于4时,Logistic方程轨道在0.75处不变化,存在不动点.在初始状态等于0.75时,精度在2时,存在着短周期现象.随着精度的增加,短周期现象得到一定的缓解.Logistic方程在高精度时也存在着短周期现象.本文从不动点附近的短周期轨道进行混沌周期研究,目标在于揭示不动点与短周期之间的关系.理论上当控制参数等于4时,Logistic方程轨道在0.75处存在不动点,但由于量化误差的作用,使得计算轨道在不同的轨道之间跳跃,破坏了原轨道的真实特性,因此,如何从真实轨道的不动点研究短周期需要解决量化误差和精度的限制.
如何降低量化误差和精度对于计算轨道的影响是解决问题的关键,下一个任务可以采用低位迭代法进行深入研究.低位迭代法能够解决量化误差对轨道的影响,避免计算轨道在不同的轨道间跳跃的问题.但低位迭代法中对于精度的基因图谱目前还未绘制完全,仅是局部的特征,因此,存在一定的困难.随着研究的深入,相信在不动点的短周期现象在不久的将来会有解决问题的方法.
参考文献
[1]刘嘉辉,张宏莉.基于可扩展精度的Logistic混沌随机序列的并行计算方法[J].中国科技大学学报,2011(9):837-846.
[2]穆爱霞.从有序到无序的混沌实例研究[J].牡丹江师范学院学报:自然科学版,2013(3):26-27.
[3]李佳.单向链式复杂网络的自适应混沌同步[J].牡丹江师范学院学报:自然科学版,2014(1):7-9.
