基于ARIMAX模型的我国GDP预测分析

杜 洁，高 珊，金欣雪

（阜阳师范大学数学与统计学院，安徽阜阳236037）

关键字：ARIMAX 模型；预测；时间序列分析

GDP 是衡量国家经济的指标之一[1]。自改革开放以来，我国的GDP 有逐年增长的变化趋势。1978-2018 年，我国GDP 年增长率平均为9.52%，1984 年达到15.14%的高峰。2018 年我国的GDP总量更是达到了13.01 万亿美元，继续稳居世界第二大经济体[2]。

中国的GDP 增速控制在合理的范围内，2019年中国经济开局良好，稳中有进。中国经济的稳定快速发展，为世界经济的复苏贡献了中国智慧和中国力量。因此，分析并预测我国GDP 的未来变化趋势，在这个“非常时刻”，对中国经济乃至世界经济都具有十分重要的现实意义。

许多学者建立了对GDP 进行研究和预测的模型，包括多元线性回归模型[3-4]，ARIMA（autoregressive integrated moving average model）模型等[5-6]。Hsin 等[7]利用纳什非线性灰色伯努利模型对金砖四国的GDP 进行了预测，证明模型是可行有效的。Schumacher 等[8]利用大因子模型对德国GDP 月、季数据进行了准确地实时预测。王红超等[9]运用指数平滑法和回归分析相结合的方法预测了2017 年我国GDP，得到满意结果。王鑫等[10]利用干预模型和BP 神经网络集成模型对我国的GDP 进行预测，发现预测误差较小。

众多预测模型中，多元线性回归模型没有考虑残差分布，ARIMA 等预测模型固然可以对GDP 进行研究，却没有考虑其它变量对它的影响。现实中，全社会固定资产投资总额会对GDP产生一定的影响。如果考虑此因素对GDP 的影响，则可以提高模型的预测精度。基于此，本文建立全社会固定资产投资总额为输入序列，GDP 为输出序列的ARIMAX（ARIMA with external input）模型，对GDP 进行预测。

1 ARIMAX 模型简介

ARIMA 模型是对单变量进行分析和预测的经典模型，如果不考虑其他变量对目标变量的影响，ARIMA 模型往往得不到满意的结果。如果将其它序列也纳入研究范围，就涉及多元时间序列分析，其最典型的模型形式为ARIMAX，即动态回归模型。对多元时间序列的分析始于1976 年，多元时间序列分析要求各变量是平稳的，否则容易出现虚假回归的情况[11]。当变量不平稳时，1987 年恩格尔和格兰杰给出了协整的定义，即虽然变量不平稳，但是回归的残差平稳，那么变量间就是协整的，此时不存在虚假回归的问题。于是多元时间序列分析的方法开始盛行[12]。

2 ARIMAX 模型的建模步骤

（1）首先，对输出变量序列{yt}和第i个输入变量序列{xit}进行单位根检验；

（2）若{xit}非平稳，则建立ARIMA 模型拟合序列{xit}，得到白噪声{εxit}

（3）对{yt}实施同样的变换，得到{εyit}:

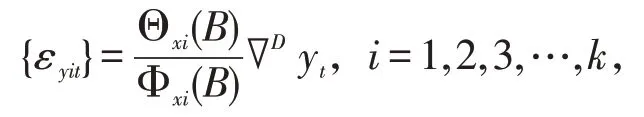
其中：D为对yt进行的差分阶数。

（4）研究{εxit} 与{εyit} 的互相关系数，确定ARIMAX 模型形式[13]，

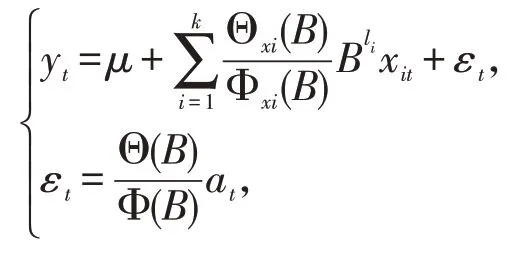
其中：μ为常数；Θ(B)=θ0-θ1B-θ2B2-…-θqBq为残差序列{εt} 的q阶移动平均系数多项式；Φ(B)=1-φ1B-φ2B2-…-φpBp为残差序列{εt}的p阶自回归系数多项式；li为B的指数；{at}为零均值白噪声序列。

3 应用ARIMAX 模型的我国GDP 预测

3.1 观测值的选取

从《中国统计年鉴》（2018）获取1980 到2018年我国GDP 和全社会固定资产投资总额（x）数据，见表1。

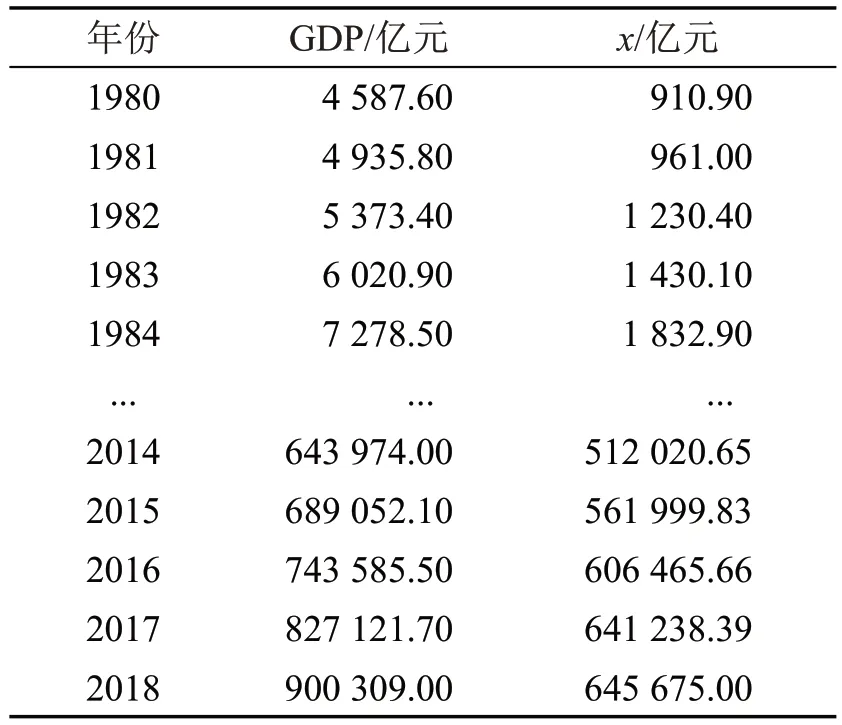
表1 1980-2018 年我国GDP 和全社会固定资产投资总额（x）（部分）

3.2 ARIMAX 模型的建立

3.2.1 检验x和GDP 及其对数和对数1 阶差分的平稳性

为满足方差齐性的要求，本文对GDP 和x进行对数化处理[14]，得到ln GDP 和lnx，对ln GDP和lnx分别做一阶差分，得到∇ln GDP 和∇lnx。运用SAS9.4，分别画出x和GDP，ln GDP 和lnx以及∇ln GDP 和∇lnx（dif ln GDP 和dif lnx）的时序图见图1。

由图1(a)和(b)，由于时序图都存在上升的趋势，容易得到GDP 和x以及ln GDP 和lnx都是非平稳的。由图1(c)可以看到时序图没有明显的趋势或者周期性变化。可以认为∇ln GDP 和∇lnx都是平稳的[15-16]。

为了精确检验∇ln GDP 和∇lnx的平稳性，对∇ln GDP 和∇lnx做ADF 检验。结果见表2～3。

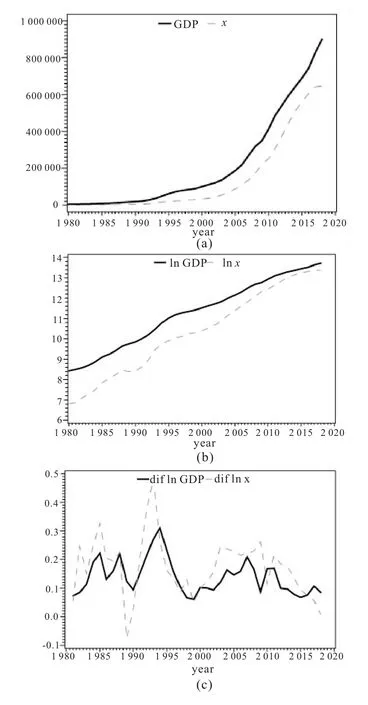
图1 时序图

表2 序列∇ln GDP 的单位根检验结果

表3 序列∇ln x 的单位根检验结果

由表2 可以得到，∇ln GDP 具有常数均值，且为平稳序列，该序列具有1 阶自相关。由表3 结果可以得到，∇lnx具有常数均值，且为平稳序列，该序列具有2 阶自相关[17-19]。

3.2.2 对∇lnx建立ARMA 模型

首先，∇lnx的白噪声检验通过，即∇lnx在0.01 的显著性水平下是非白噪声，∇lnx有信息可供提取，可以建立ARMA（autoregressive moving average model）模型。

其次，由AIC 及SBC 准则，最终得到疏系数模型AR(1,4)为条件最优模型[20]，并得到残差{εi1}为白噪声，因此模型显著。常数μ及φ1,φ4的估计及{εi1}的白噪声检验结果分别如表4 和5。

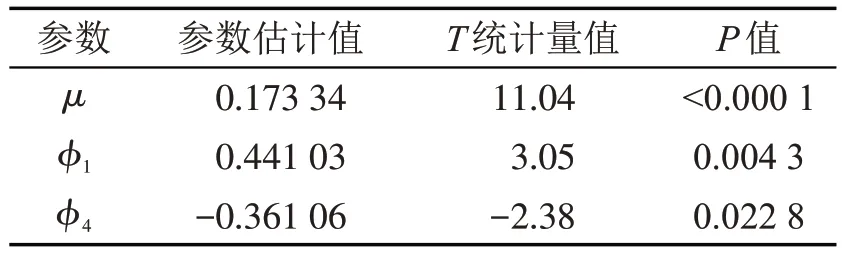
表4 对∇ln x 建立ARMA 模型参数估计结果

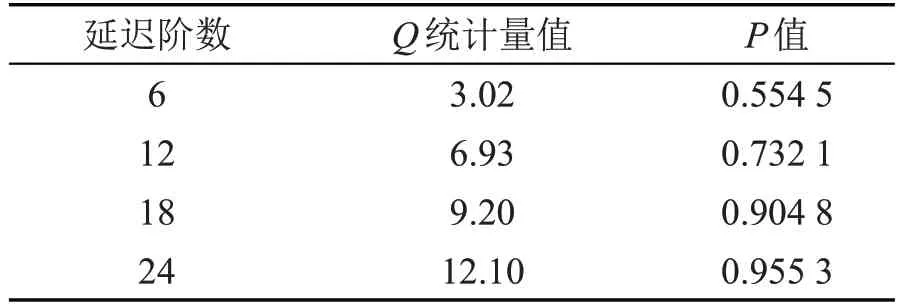
表5 ∇ln x 建立ARMA 模型残差白噪声检验结果

拟合模型为

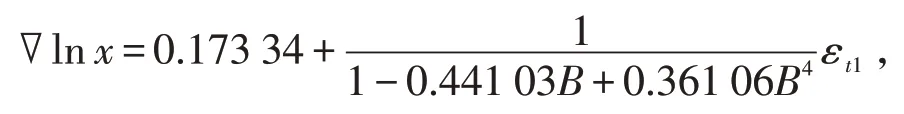
其中，{εt1}为白噪声序列。

对∇ln GDP 实施同样的变换，即

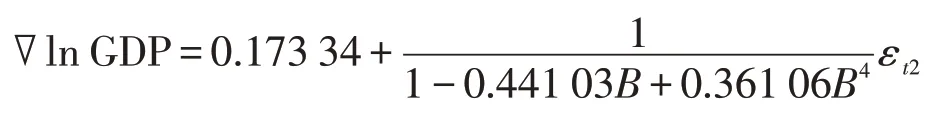
得到{εt2}。

3.2.3 建立ARIMAX 模型

考察{εt1} 和{εt2}之间的互相关系数。显示∇ln GDP 和∇lnx在延迟0 阶时最相关。因此将∇ln GDP 和∇lnx滞后0 期建模[21]。

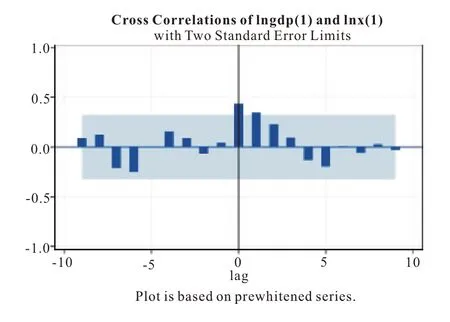
图2 {εt1}和{εt2}之间的互相关系数图

经试算，对∇ln GDP 和∇lnx建立的模型为

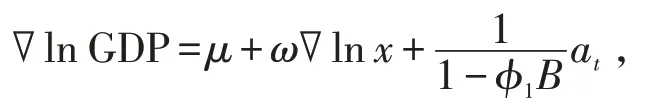
参数估计结果如表6 所示。ARIMAX 模型为：

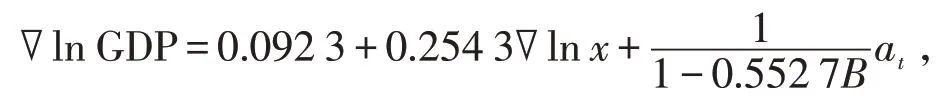
模型参数显著。

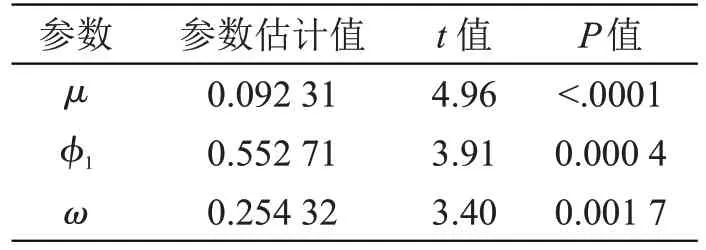
表6 ARIMAX 模型参数估计结果

at的白噪声检验无法拒绝原假设[22]，即模型已经充分提取了序列的信息。且互相关检验结果显示at和ln x 的互相关函数在显著性水平为0.01时为0[23]，说明模型有效。

4 ARIMAX 模型预测

利用ARIMAX 模型对ln GDP 进行向前2期，向后5 期预测结果如表7。换算成GDP 预测结果如表8。

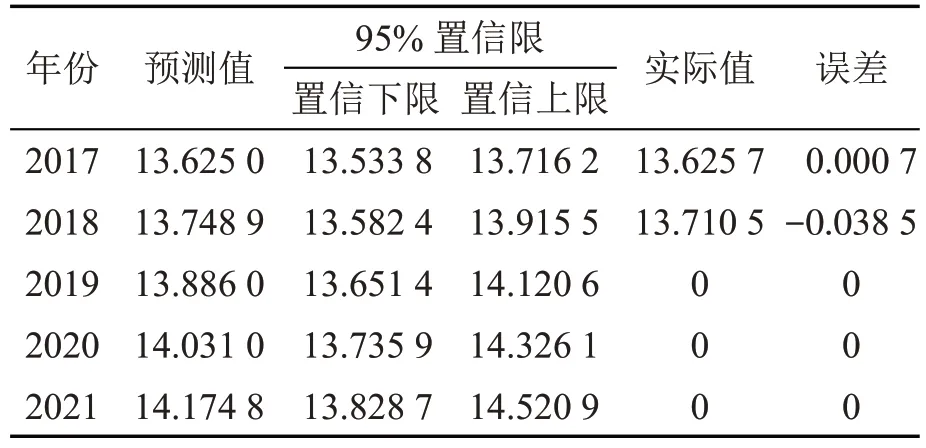
表7 ARIMAX 模型预测结果

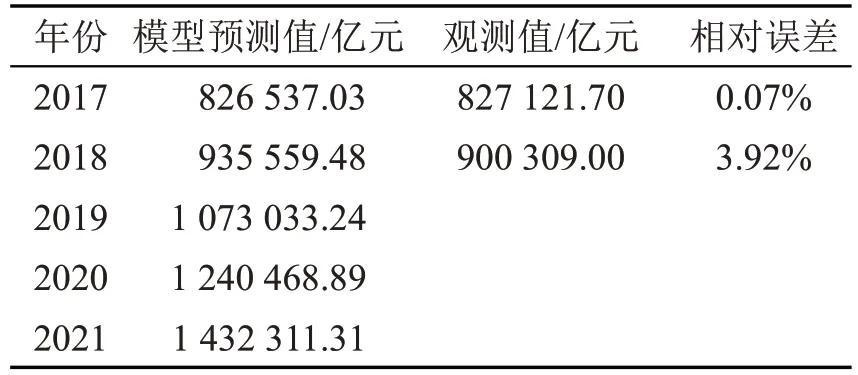
表8 取指GDP 预测结果

由2017 和2018 年的预测结果可见，GDP 预测相对误差均不超过5%，预测较为准确[24]。

5 预测结果比较

如果不考虑全社会固定资产投资总额对GDP的影响，选取ARIMA 模型对1980-2018 年GDP进行建模，并预测未来我国2019-2021 年的GDP的值，拟合的AR(5)模型为：

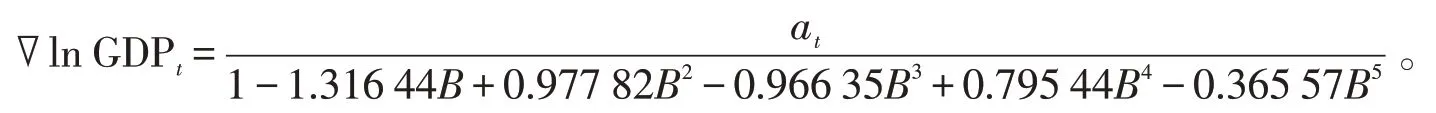
预测结果见表9

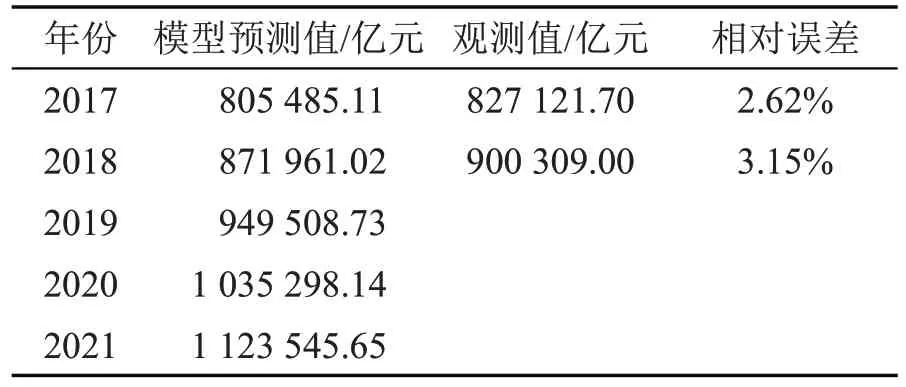
表9 ARIMA 模型预测结果

可见，ARIMAX 模型的预测MAPE（mean absolute percentage error）为1.995，ARIMA 模型的预测MAPE 为2.885。因此，ARIMAX 模型比ARIMA 模型预测更为准确。

6 图形拟合

为了更形象地观看拟合效果，画出拟合效果图如图3。图3(a)为ln GDP 的拟合图。星号代表实际值，中间虚线和两边实线分别代表拟合曲线和95%置信曲线。图3(b)为GDP 的拟合图，可见两图拟合效果都很好。

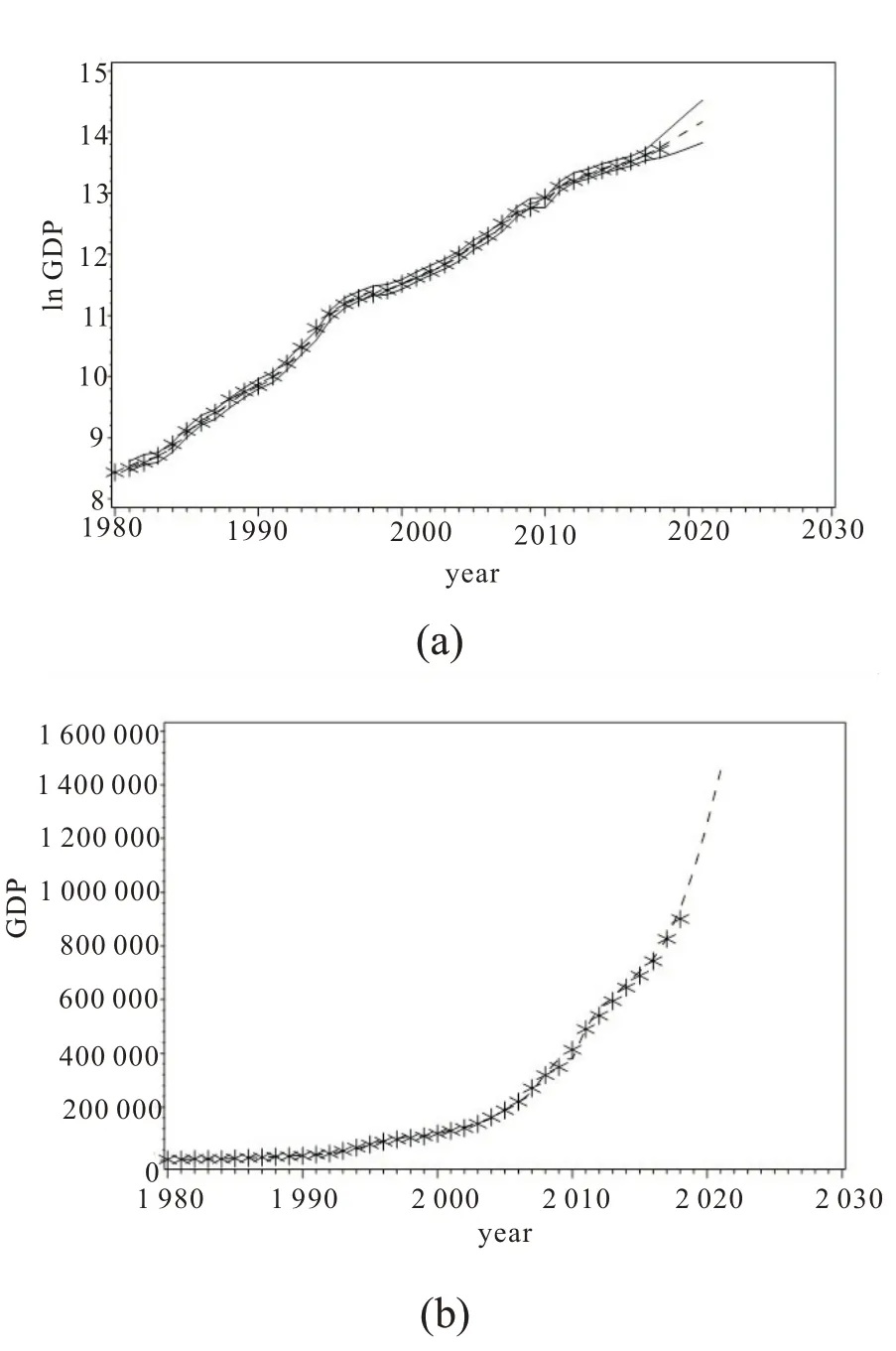
图3 ARIMAX 模型拟合效果图

7 小结

因为GDP 和许多因素相关，考虑到全社会固定资产投资总额和GDP 有较大的关联，因此把全社会固定资产投资总额作为变量引入到GDP 的预测模型当中，建立了ARIMAX 模型。结果显示，2017 年和2018 年的预测相对误差分别为0.07%和3.92%，均不超过5%，预测较为精确。将两者的预测结果计算MAPE 发现，ARIMAX 模型的预测结果较ARIMA 模型的预测结果更为精确。这也说明了全社会固定资产投资总额对我国GDP 具有一定的影响，将它加入预测模型中是合理的。