基于风险熵的农产品安全定量评价研究

陈志军 刘 艳 钱永忠

（1.中国农业科学院农业质量标准与检测技术研究所，北京 100081；2.农业农村部农产品质量安全重点实验室，北京 100081；3.国家农产品质量安全数据中心，北京 100081）

1 引言

由于农兽药残留等潜在危害物在农产品中的含量水平往往低于仪器的检出限，监测样品的大多数检测值被记录为“未检出”，农产品安全监测数据呈现出高度的稀疏性[1-2]。为避免因有效信息不足而无法获取准确的决策参考信息，监测工作通常需要设置足够大的样品抽样量[3-4]。然而，在国家层面上，受监测成本的限制，要保证品种、地区、季节等多个分析维度上都有足够的抽样量是十分困难的，往往需要将不同年份、不同地区、不同监测工作的多源数据融合在一起使用[5]。由于不同工作背景的差异性，多源监测数据是异构的，在产品、种类、检测指标上一般有较大的差异，数据的融合使用需要一个有效的融合机制。

在安全性评价上，目前主要有两种方法：一种是基于限量值进行定性判定，不论是微观层面上对单个产品安全性进行评价，还是宏观层面上对某一区域或某类产品总体安全状况的评价，都基于合格率或超标率展开[6]；另一种是引入膳食暴露评估模型，将监测数据与产品消费调查数据、居民健康调查数据进行关联，通过计算机大规模模拟的方式对潜在危害物的健康风险作出评估[7-8]。上述两种方法中，第一种方法的分析结果容易理解，但结果较为粗糙和保守，分析过程会有大量有效信息的损失，且消费者对定性评价结果高度敏感，容易引起消费恐慌；另一种方法需要跨部门数据的关联应用，分析过程复杂，结果释读和理解困难，难以保证监管决策所需的时效性。

本文拟引入熵值的概念，尝试构建一种以计算风险熵为目标的多源异构监测数据融合方法，并围绕风险评估与预警的实际应用需求，并对基于风险熵的宏观定量评价应用开展初步探讨。

2 原理与方法

2.1 风险熵及其构建

2.1.1 样本矩阵

设某一监测工作共涉及N个样本，k个农产品、p个指标，第i个农产品的抽样量为。以单个样本为行、指标为列，指标的检测结果为元素，则某一农产品的监测数据可定义为如下监测矩阵：

上述Mi矩阵中的任意元素有2种可能的取值，一种为“ND”，意为“未检出”；另一种为仪器检测值。由于监测数据的高度稀疏性，Mi矩阵中元素取值的大多数甚至是全部为“ND”。

将所有产品的监测矩阵纵向拼接，则该项监测工作所得全部监测数据可定义为样本矩阵M=(M1,M2,…,Mk)′N×p。为便于后续分析，可将M矩阵中的“ND”值替换为1/2 LOD 值（LOD 为仪器的检出限）。为避免混淆，仍记替换后的矩阵为M。

2.1.2 多个样本矩阵的融合

多源异构数据融合的目标是将多项监测工作的样本矩阵融合为一个新的样本融合矩阵M*。由于工作背景的不同，不同监测工作所关注的产品和指标有很大的差异，要构建新的样本融合矩阵M*，需要从产品、指标两个维度的融合入手，并考察融合后的产品抽样量ni*。本文提出一种新的数据融合方法。

就产品而言，需要考虑一下三种情形：（1）产品名称一致。这种情形下样本数据可直接融合；（2）产品名称有差异，但产品类别一致。对于这种情形可按特定分类标准将相同类别产品的样本数据进行融合；（3）产品和类别均不相同。这种情况下可将小样本产品归类为“其他”，保留大样本产品名称。与情形（1）可以关注到具体产品不同，情形（2）和情形（3）在完成数据融合后，类别将作为后续数据分析与应用的关注点。按产品对数据进行融合后，需要考察抽样量ni*。一般而言，需要根据分析层级确定最小抽样量ns，并将ni*＜ns的样本数据归入“其他”。这里的分析层级是指数据融合的工作层面，如在国家或省级层面开展监测数据的融合应用。关于这一问题，陈志军等提出了一种最小抽样量的设置方案[9]。对指标维度的融合，取各样本矩阵中指标的合集作为样本融合矩阵M*的列即可。但由于该合集的指标数p*≥p，样本融合矩阵M*中的元素将出现第三种取值“NULL”，表示融合前的样本没有对该指标进行检测。

上述数据融合过程完成后，总的抽样量N*、农产品个数k*、指标数p*、单个产品的抽样量ni*都将增大，这无疑大大增加了后续分析所需的有效信息量。但同时也不难发现，样本融合矩阵M*仍然是稀疏性的，含有一定量的“NULL”值。为满足分析的需要，我们需要构建一个以产品为行、指标为列、各行产品名称具有唯一性的新矩阵。为实现这一目标，下文将讨论特定“产品+指标”组合下风险熵的构建。

2.1.3 风险熵

熵（entropy）是一个热力学概念，用于度量物理体系的混乱程度。熵值越低，体系内微观粒子越活跃；熵值越高，体系内微观粒子的运动越趋向静止[10]。Shannon[11]借鉴了热力学中熵的概念提出了“信息熵”，用以度量一个系统内信息的含量。本文拟基于熵与信息熵的基本概念，试述特定“产品+指标”组合下风险的度量问题。

为避免符号的混乱，仍设某一产品共采集了ni个样本，每个样本检测p个安全指标，xlj为第l个样本、第j个指标的检测值（l=1,2,…ni；j=1,2,…p）。定义风险值：

（1）式中，slj为限量标准值，其量纲与xlj相同；rlj是无量纲的比值，是对第l 个样本、第j 个指标潜在风险的定量度量。由此，可以定义风险熵：

上文中提及用1/2 LOD 值替换“ND”值，这是为了避免xlj和rlj取值为零，继而根据（4）式计算的hlj取值为零，造成（2）式的计算无法继续。

按照上述方法考察样本融合矩阵M*中的所有“产品+指标”组合，即可获得以风险熵值为元素组成的k*行、p*列风险熵矩阵E：

在上述矩阵E中，每一行代表一种监测产品（类别），每一列代表一个监测指标，所有元素都有明确的定量取值，可以很方便地对其进行进一步处理与分析。

2.1.4 风险熵的意义与基本性质

风险熵是基于风险值构建的，它反映的是某一安全指标在特定产品上的风险程度。由于大多数样本的检测结果是“未检出”，大多数rlj的取值相同，这些相同的取值可作为背景值考察。当检出样本的数量增加、检测数值增大时，取背景值元素的数量将减少，rlj的取值将增大，这时可视为该“产品+指标”组合中风险的混乱程度增加，有效的风险信息增加。由（2）式、（4）式可知，风险熵elj∈[0,1)。当“未检出”样本数越多时，风险熵的取值越小，越趋向于0；当全部样本都为“未检出”时，风险熵取最小值0，表示未发现有效风险信息，可认为该“产品+指标”组合处于绝对的安全状态；当样本间的风险值差异越大，该“产品+指标”组合的风险熵取值越大，更趋向于1。上述风险熵的意义与风险的基本认知是一致的，以农药残留为例：农药施用量越大、施用的越频繁，在单位时间内就越容易形成更大残留量，造成风险熵的取值增大；反之，风险熵的取值将减小；若不对农产品施药或是休药期足够长，则风险熵取值为0。

从上述风险熵的意义可以看出，风险熵与热力学中熵的概念有很大相似性，两者都是对体系混乱程度的度量。在对风险的定量方法上，风险熵对风险大小的定量与信息熵对信息量的定量也很类似。不难发现，与信息熵类似，风险熵也有三个基本性质：（1）单调性，未检出的样本越多，“产品+指标”组合携带的风险信息越低；（2）非负性，风险熵是一种较为宏观的广度量，非负性是一种合理的必然；（3）累加性，即考察多个安全指标时，总风险是可以用各个指标的风险熵之和来描述的，这也是一种宏观的广度量。

2.2 宏观定量评价方法

由上文可知，风险熵是基于融合数据对特定“产品+指标”组合的风险程度的度量，其本身的取值就可以用于该“产品+指标”组合安全性的定量评价，用以发现潜在的风险来源。此外，由于风险熵是可累加的宏观广度量，这为基于风险熵矩阵E开展农产品安全性的宏观定量评价提供了可能。

综合评价是一种提取对象主体（常为复杂系统）的本质属性，对评价对象进行度量的方法，广泛用于多属性决策。郭亚军[12]归纳了综合评价的基本理论与方法，其评价过程主要包括评价指标的预处理、确定指标的权重、选择和构造综合评价集结函数等步骤。下文拟基于数据融合所得的风险熵矩阵E，按照综合评价的流程尝试在宏观层面对农产品的安全性做出定量评价，并对各产品（类别）的风险值进行排序。

令Li为第i个产品的综合评价值（可视为该产品安全性的宏观评价指数），wij为第j个指标的权重，依照“线性加权综合法”：

上式中，wij∈[0,1]，且=1。权重wij取值的确定有多种方法，本文采用客观赋权法中的熵权法[13]。

3 实例数据分析

3.1 数据来源

本研究所用的实例分析数据来源于农产品质量安全风险监测信息系统（www.lxjc.aqsdc.com），该数据涉及同一年度两项国家层面的蔬菜中农药残留监测工作。按照NY/T 3177-2018的农产品分类规则[14]，取最小抽样量ns=500，数据融合前后的基本信息如下：

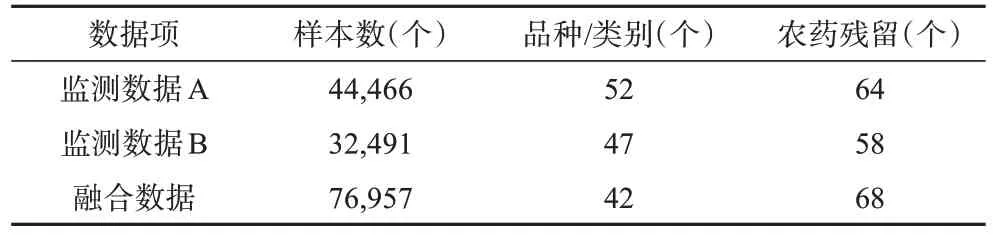
表1 监测数据与融合数据的基本信息Table 1 Basic information of monitoring and fusion data

3.2 结果与分析

设置P50、P80、P90、P95 百分位数为安全阈值划分标准，图2 展示了蔬菜中各农药残留风险熵取值的分布情况和安全阈划分结果。从这一经验分布可以看出，蔬菜中绝大多数农药残留处于相对安全的水平，约有95%左右的“蔬菜+农药”组合其风险熵值在0.5以下。只有极少数比例的“蔬菜+农药”组合的风险熵值接近于1，这为后续风险源的识别提供了便利。

由于风险熵值越大代表风险越高，故综合评价值Li越高的蔬菜产品的总风险越高。表2 列出对所有农药残留进行加权后各蔬菜产品的综合评价值及其风险排序结果。根据表的排序结果，芹菜、豇豆等产品的总风险较高，其风险值约比安全性较好的南瓜、金针菇等产品高出两个数量级。

为探索潜在风险所在的具体“产品+指标”组合，可将风险熵值绘制成矩阵式热力图进行排查。图3展示了蔬菜中各农药残留的风险热力分布及其根据热力分布获得的产品聚类结果。由图3 可知，通过聚类处理后，可将风险熵值和潜在风险较高的“产品+指标”组合集中聚拢在一起，这对风险管理上考察哪些产品中的哪些监测指标需要重点关注？单个产品中多个指标的混合问题是否严重？高风险指标主要分布在哪些产品中？等关键问题具有重要的参考价值。

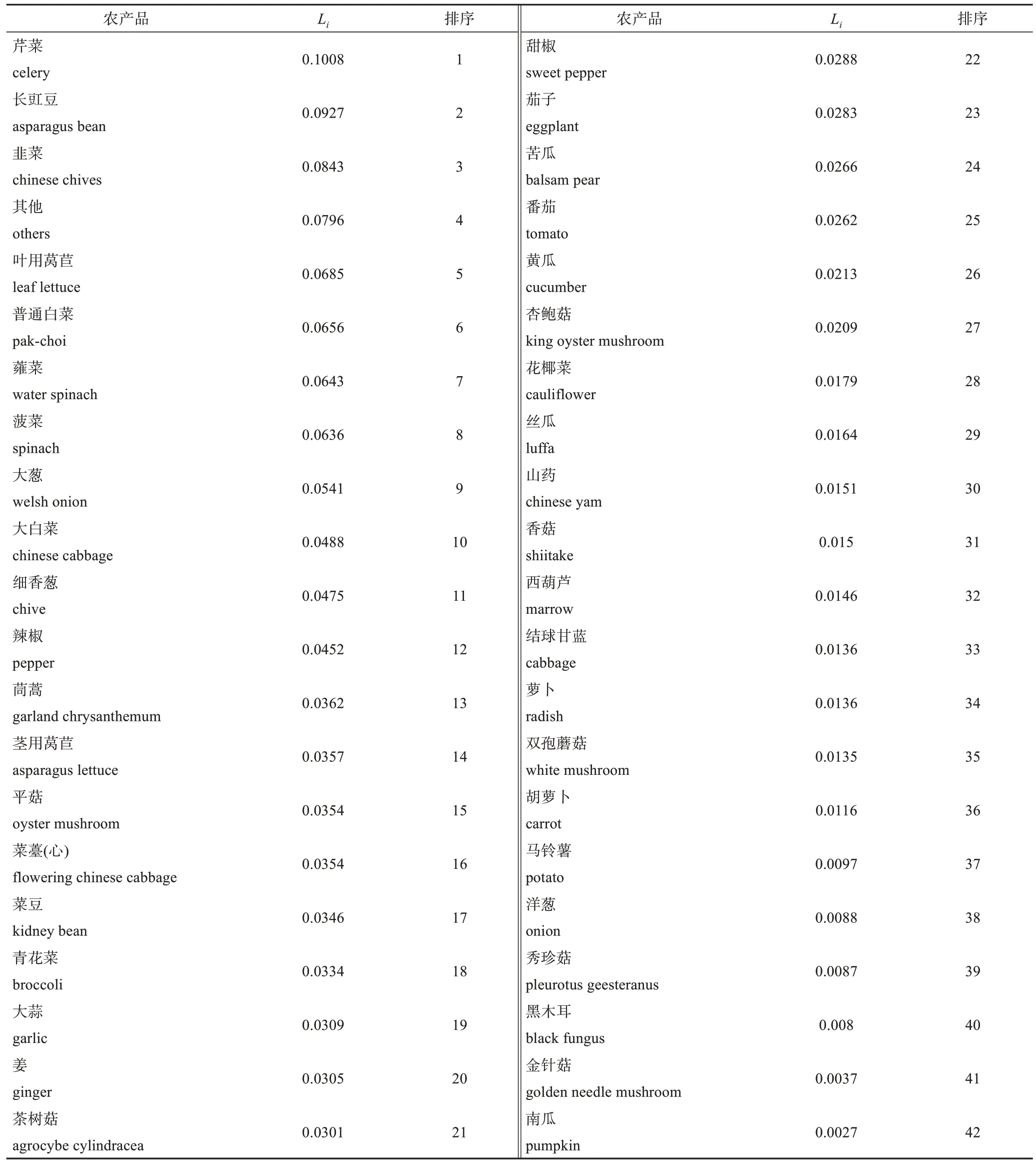
表2 蔬菜中农药残留安全性的评价结果Table 2 Safety evaluation results of pesticide residues in vegetables

通过综合评价值与超标率的比较可知，两者在风险大小的识别上存在一定差异。图4 展示了42 种蔬菜的综合评价值与超标率之间的关系。按照常规的认知，如果综合评价值与超标率对风险大小的识别能力较为一致，则图4 中的点应该集中分布于灰色斜线附近。而图4 中被圈出的点显然离灰色斜线较远。考察黄色圈中的蔬菜产品，发现这些产品中残留的超标情况较为集中的分布与少数几个农药中，其他大多数农药的风险值较低。考察红色圈中的蔬菜产品，发现这些产品中残留的超标情况较少发生，但是产品中多个农药残留检出的情况较多。这说明，综合评价值在宏观水平上较好地克服了定性评价易受单个指标超标情况的影响、无法识别混合风险的不足，在对风险大小的识别上具有更高的准确性。

4 讨论

本研究提出了一种以计算风险熵为目标的数据融合策略，为多源异构监测数据的整合应用、解决单项稀疏型监测数据有效风险信息不足的问题提供了一个新的方案。风险熵是一种宏观层面上对风险进行定量描述的指标，该指标的构建以限量标准为基础，且指标值不带量纲，可以避免将定性指标用于宏观层面评价所带来的风险识别不够准确、评价结果容易引起消费恐慌等问题。但这一定量风险指标如何进一步论证与应用，是值得认真研究的问题。本文基于综合评价理论与方法开展了农产品安全性宏观定量评价研究，这仅是对风险熵分析应用的一种试探性尝试，证明其分析过程在技术上有较好的可行性，尚有很多技术细节需要处理。如，风险熵是一个有值域的指标，对这类指标进行分析需要有合理的数据转化方法，直接使用指标值进行分析可能会存在方法的适用性问题；综合评价应用的关键是指标权重的确定和集结函数的选择，近年来，DEA 法[15]、TOPSIS 灰色关联分析法[16]、组合评价法[17]等方法不断涌现，这些方法对农产品安全性评价的适用性如何，该如何评判和选择，也需要深入开展论证。另外，风险熵矩阵E是一个信息完全的二维数组，对这类数组的统计分析方法很多，相信除综合评价法外，尚有其他可用于农产品宏观定量评价的方法。如何针对风险管理的需求，有针对性的设置分析主题，并在方法和信息化应用上有所创新，需要后续深入开展研究。

在工作层面上，农产品安全监测数据的融合与应用需要监管、抽样、检测等多个工作体系、多个工作层级的共同支撑，这对整个风险管理工作的组织性和协同性提出了更高的要求。在制度上建立一套可行的数据汇交、共享与应用的有效机制，应是开展农产品安全宏观评价等风险大数据应用不可或缺的重要保障。

5 结论

本文围绕农产品安全风险管理需求，提出了一种以计算风险熵为目标的数据融合策略，并应用综合评价理论与方法，开展了基于风险熵的农产品安全性宏观定量评价研究。实例数据分析过程表明：风险熵能够有效提取融合数据所包含的风险信息并对其进行定量；基于风险熵的安全性评价可以给出完整的风险阈值划分与风险排序结果；风险熵对潜在风险的识别更为准确，可以避免定性评价对风险的过高或过低估计。这说明，围绕风险熵的数据融合与宏观定量评价在技术上是可行的，能够为农产品安全风险管理工作提供更加准确的参考信息。