逻辑推理的心理学研究及其对小学数学教学的启示
2020-03-15宋恒欣喻平
宋恒欣 喻平
摘要:心理学对逻辑推理中演绎推理、归纳推理和类比推理的能力发展和影响因素等做了一系列的研究。将这些研究的成果应用于小学数学教学,可以提出三条教学策略:关注年龄阶段,开展分级训练;结合知识经验,创设推理场景;梳理推理内容,把握培养时机。
关键词:逻辑推理演绎归纳类比小学数学
按照《普通高中数学课程标准(2017年版)》的定义,“逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养。主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎”。本文简要介绍心理学关于逻辑推理的一些研究,并讨论如何将这些研究的成果应用于小学数学教学。
一、心理学关于逻辑推理的一些研究
(一)演绎推理的研究
1.演绎推理能力的发展。
方富熹等将270名被试按照9、12、15岁分为三组,同时考察了不同学校类型、家长文化程度以及学生智能发展水平对假言演绎推理能力发展的影响。他们使用了三套内容与生活有关的试题,采用口头报告的形式,即由主试说出假言判断的前提,让被试在无误地复述之后,就主试提出的问题进行推导并阐述理由。研究结果显示,儿童充分条件假言演绎推理能力从9岁开始发展并随着年龄的增长而提高,9岁为开始发展水平,12岁为过渡阶段,15岁为成熟水平。该研究还指出,被试的家庭教育背景、学校教育条件等外部条件以及智能水平、学习能力等内部因素都影响着其假言推理演绎能力的发展。
李丹等选用能够反映事物之间蕴含关系并且与生活联系较多的命题来考察儿童的演绎推理能力,选取了从小学三年级到初中三年级七个年级的495名被试,让他们完成20道假言演绎推理的选择题。研究结果显示,小学三年级到初中三年级学生的假言演绎推理能力随着年龄的增长而增长,并且初中一年级左右是一个快速增长的关键期。在实验中,他们选取了两所教学水平不同的学校做对照,经过测试发现,高教学水平的学校学生的推理能力发展领先低教学水平的学校一个年级;通过对教师的访谈发现,在教学中注意培养、训练学生的逻辑思维能力有助于其推理能力的发展。
选言推理是其中一个前提为选言判断,另一个前提对这个选言判断的一部分选言肢进行肯定或否定的演绎推理。选言推理可分为不相容选言推理和相容选言推理。不相容选言推理以不相容选言判断作为大前提。其推理规则是:肯定一个选言肢,可以否定其余的选言肢;否定一个选言肢,对于选言大前提含兩个选言肢的选言推理可以肯定另一个选言肢,对于选言大前提含三个选言肢的选言推理则不能肯定另外两个选言肢中的任何一个。相容选言推理以相容选言判断作为大前提。其推理规则是:肯定一个选言肢,不能否定其余的选言肢;否定一个选言肢,对于选言大前提含两个选言肢的选言推理可以肯定另一个选言肢,对于选言大前提含三个选言肢的选言推理则不能肯定另外两个选言肢中的任何一个。吴荣先选择从小学三年级到初中三年级,每个年级对应于一个年龄组,从9.5岁到15.5岁(每个年龄组的范围为±3个月)共七个年龄组的学生为被试,考察了不同年龄段学生选言推理能力的发展情况。研究结果显示,学生的选言推理能力随着年级的增加而不断发展,而相容选言推理能力和不相容选言推理能力的发展是不平衡的:在小学四年级就基本掌握不相容选言推理,而到初中三年级才基本掌握相容选言推理。
图形推理是指借助图形来推理的过程。林崇德等探讨了小学生图形推理策略的差异,将145名小学生按照数学能力分为三个对照组,并将从CRT瑞文智力测验中选出的14道题根据图形关系分类,对学生进行测试。他们将儿童的推理策略分为6类:(1)分析策略,指能够正确发现规律并用以解决问题;(2)不完全分析策略,指能够发现部分规律并用于解决问题;(3)知觉分析策略,指不能明显抽象出规律,但能发现一些变化,并根据这些变化做出选择;(4)知觉匹配策略,指倾向于选择相似或完全不同的图形作为答案;(5)自主想象策略,即凭借个人喜好进行选择;(6)格式塔策略,即把缺损图形补充完整的策略。研究结果显示,不同年龄的儿童在推理策略选择上有着不同的特点:总的来看,在小学阶段,知觉分析策略占主导地位,且分析策略的使用随年龄的增长而上升;二年级开始,学生的图形推理能力有较大飞跃,到了五、六年级,学生能够不受题目形式的影响,从本质上把握逻辑规则。
2.影响演绎推理的因素。
方富熹等为探查12岁儿童充分条件假言演绎推理能力的差异,选择12岁的“普通儿童”与“数学成绩优异儿童”各20人,分别采用与生活经验联系密切、与生活经验相悖和比较抽象的三套试题进行个别测试。测试结果显示,12岁的儿童普遍具有充分条件假言演绎推理的能力,但是他们的推理过程容易受到材料内容性质和自身生活经验的影响;同时,“数学成绩优异儿童”的假言演绎推理能力更强,说明儿童假言演绎推理能力与其智能水平有关。
李国榕等根据直言三段论推理的四种格(全称肯定、全称否定、特称肯定和特称否定)、“四概念错误”(把两个不同概念当作同一概念使用,导致在三段论中出现四个概念)和“特称前提推出错误结论”等三个类型,编制了含20道推理题的问卷,对在升学率分别为低、中、高的三所普通中学的学生进行测试。测试结果显示,中学生直言三段论推理是否正确和推理的格密切相关,其中全称肯定型的成绩最好;并且,学习成绩的高低也影响着推理能力的发展。
沃建中等研究了小学生在图形推理中策略选择的问题。结果发现,在解决简单的问题时,不同水平的学生在策略选择上无明显差异,大部分学生都采用分析策略,都能找到规律完成题目;然而随着难度的增加,不同水平的学生在策略选择上出现了差异,高水平的学生多使用分析策略和知觉分析策略,中等水平的学生多使用知觉分析策略,而低水平的学生多使用知觉匹配策略。结合访谈还发现,低水平学生的问题表征方式造成他们不能正确进行图形推理,也影响了他们推理策略的选择使用。
(二)归纳与类比推理的研究
1.归纳与类比推理能力的发展。
林崇德把运算中的归纳推理分为四个水平:(1)直接归纳推理(如由6+0=6,8+0=8,…归纳出“任何数加零等于原来的数”);(2)简单文字运算中直接归纳推理(如由x=y,x+a=y+a,x+b=y+b,…归纳出“等式两边加上一个相同的数,仍然相等”);(3)算术运算中间接归纳推理(如通过多个步骤的分数运算归纳出分数的性质);(4)初步代数式的间接归纳推理(如通过多次对两个变量的运算归纳出两者的函数关系)。他的研究表明,小学阶段随着年龄的增长,学生的归纳推理能力逐步提升,在五年级基本达到“算术运算中间接归纳推理”的水平。
倪斯杰等对小学二年级学生数学归纳推理能力的研究显示,该年龄段的学生基本不具备所考察的归纳推理能力,具体包括通过归纳理解新概念、从多步算式中找规律、从图形变换中找一般规律等。而Csapó对三、五、七、九、十一五个年级2400多名学生归纳推理能力的研究表明,三年级学生已经具备了一定的归纳推理能力;低年级学生得分的标准差较大,原因是少数学生在早期就具备较强的能力;五至七年级是归纳推理能力发展最迅速的时期,九年级后发展明显变缓。
类比推理能力的发展研究关注的一个问题是类比推理能力何时出现。传统代表如皮亚杰认为,类比推理能力的发展与从具体运算到形式运算能力的发展一致,儿童要到11—12岁才能真正地完成。后来的许多研究发现,类比推理能力的发展明显早于皮亚杰所说的形式运算阶段。大多数研究者都认为,类比推理能力在前运算阶段便得到了有效的发展,在较熟悉的事物中,3—4岁的儿童就能成功地完成类比推理作业。
费广洪等随机抽取了180名3—11岁的儿童,整合多种类比推理材料,采用关系图形、几何图形、词语、数字、故事等五种材料,考察儿童类比推理能力发展的年龄特点。研究发现,儿童的类比推理能力发展有阶段性的特点,4—5岁开始能够进行类比推理,并且随着年龄的增长,类比推理能力不断上升。
2.影响归纳与类比推理的因素。
已有研究发现,对事物之间相似性的认知是归纳推理的基础。相似性研究中的一个关键问题是知觉相似和概念相似之间是如何相互作用的。知觉相似观认为两个物体之间的相似性主要是基于表面的物理特征,概念相似观认为相似性主要取决于物体之间共同的关系。孙红梅等对这个问题做了进一步的研究,结果发现,一年级学生和三年级学生在基于知识和基于外观的推理之间不存在显著性差异;而五年级学生和大学生基于知识的推理次数显著高于基于外观的推理次数,同时五年级学生和大学生在基于知识的推理上没有显著差异。这一研究结果暗示,五年级学生在归纳推理时与成人的表现相一致,主要基于概念相似;一年级学生和三年级学生在基于概念的归纳推理方面还处于过渡期。
促使儿童类比推理能力发展的潜在因素是什么?研究者们的看法大致有三类:(1)能力的限制。例如,儿童类比推理能力的发展主要受诸如记忆容量、信息加工能力等认知能力的限制。(2)知识经验的限制。例如,儿童在类比推理中存在显著的年龄差异,而造成这种差异的原因是知识经验的积累。如果给儿童熟悉的类比任务,让他们运用熟悉的知识进行推理,那么,他们将表现出类比推理能力。(3)既有能力的影响,也有知识经验的影响。
王树芳等以任务难度和反馈学习为自变量,对儿童类比推理做了实验研究。反馈学习是指儿童完成一个类比推理任务后就反馈是对还是错:如果对了,就让儿童说出类比的关系,从而确保他们是理解类比关系的;如果错了,就解释源图的事物,让儿童自行明白源图事物之间的关系;如果经过三次解释,儿童还是不明白这种关系,就直接说明。结果发现,开展反馈学习以降低任务难度时,7—8岁儿童能完成更高年龄段儿童才能完成的任务;但是,增加任务难度时,11岁以上儿童也表现出类比推理能力的弱化。结果提示,儿童能否在类比推理任务中表现出相应的能力可能取决于任务难度,而反馈学习可促进一定年龄段内儿童的类比推理能力发展。
(三)逻辑推理能力培养的研究
胡卫平等开发了面向所有学科的“学思维”活动课程,每个活动都包括四个环节:第一,活动导入,即创设情境,引起学生认知冲突、激发学生学习兴趣的环节;第二,活动过程,即按照活动的内部结构,组织学生观察、思考、讨论、实验的环节;第三,活动心得,即引导学生回顾整个活动,总结心得、引起反思的环节;第四,活动拓展,即向生活和其他学科领域拓展思维方法的环节。通过实验发现,实验组学生思维能力的总体水平以及发展速度显著快于控制组学生;实验组学生在归纳推理、演绎推理、空间认知、类比推理和抽象概括能力上显著高于控制组学生,且除了抽象概括能力,其他四项能力的发展速度显著快于控制组学生。
陈德煜等对小学三年级学生开展了数学思维训练的实验研究。数学思维训练是指用一定时间有意识地安排逻辑思维方法,结合教材内容编写训练题,给学生学习与练习。分为7个单元:(1)概念理解与数量关系;(2)概念的聯系与判断;(3)比较、抽象、概括和推理;(4)分析和综合;(5)认清条件,分析和解决问题;(6)一题多变、一题多解,训练思维的灵活性;(7)解决难题。实验表明,实验班学生的逻辑思维能力得到了明显的提升。
王瑾认为,小学生的归纳推理能力训练应当分为四个阶段。(1)前归纳阶段(一年级):初步掌握观察的方法,养成观察的习惯;通过简单的分析与比较活动,发现共同性与差异性,初步了解什么是规律,会做简单的分类;积累观察、分析、比较、分类的经验;具有归纳推理的潜意识。(2)归纳推理的初级阶段(二、三年级):学会根据适当标准分类;形成对规律的基本认识,能提出一些简单的猜想,会用自己的语言或数学语言加以表征;积累相关的数学活动经验。(3)归纳推理的完善阶段(四、五年级):深化枚举归纳推理获得一般结论(猜想)的活动,特别是,使用枚举归纳推理于运算法则、规律性公式的形成;通过错误猜想,懂得枚举归纳所得的结论具有或然性,从而明确检验的必要性,并能用反例推翻错误猜想。(4)归纳推理的前演绎阶段(六年级):深化枚举归纳推理,使用枚举归纳推理于运算法则、规律性公式的形成;结合数的运算法则和运算性质的学习,逐渐增加演绎成分,而引进计算推证和科学归纳推理,从而通过个别事例的分析,发现因果关系(必然联系),获得解释一般结论的内在根据,特别是,使用科学归纳推理于运算法则、规律性公式的形成。
二、对小学数学教学的启示
从以上研究可以看出,不同类型的逻辑推理有着不同的影响因素,同时存在年龄和认知发展顺序这样共性的影响因素。小学数学教学中,围绕培养学生逻辑推理能力的目标,可以考虑采用如下一些策略:
(一)关注年龄阶段,开展分级训练
如前所述,小学生逻辑推理能力的发展有年龄阶段的规律。一、二年级属于启蒙阶段,教师应当教学生观察事物的方法,学会通过观察对事物进行分类,这是逻辑推理的起点。三年级是关键时期(是儿童从具体形象思维向抽象逻辑思维过渡的转折点),从这时起,教师应当结合教材中的知识,有意识地对学生开展逻辑推理的训练,包括演绎推理、归纳推理和类比推理;并且随着年级的升高,适当加大训练材料的难度。
在逻辑推理的训练中,教师还要充分考虑学生的认知水平。归纳、类比等合情推理更容易为小学生所把握,而逻辑性更强的演绎推理更重要的发展阶段是初中二年级。所以,小学生逻辑推理的训练,重点应该放在合情推理上,没有必要过分关注演绎推理(谨防揠苗助长)。当然,也要注意演绎推理的渗透,让小学生经历由探索猜测到合理证明的过程,感受由合情推理到演绎推理的过程,从而更加深入地理解知识的内涵,体会数学的严谨性,并发展相应的逻辑推理能力。
例1利用计算器计算15×15,25×25,…,95×95,并探索规律。
利用计算器计算出算式结果后,中年段的学生可以通过观察积与乘数的关系,运用归纳推理发现一些有趣的规律,如15×15=225=1×2×100+25,25×35=625=2×3×100+25,35×35=1225=3×4×100+25,…。而高年段的学生学过用字母表示数,可以尝试采用演绎推理的思想证明上述规律:若用字母a表示一个正整数,则有(a×10+5)×(a×10+5)=100×a2+2a×10×5+25=a×(a+1)×100+25。这是一个由特殊到一般的过程,既包含了归纳推理,又包含了演绎推理,是一种训练逻辑推理的良好形式。
例2(1)将下面的数分类:3,5,13,23,25,35,45,53。
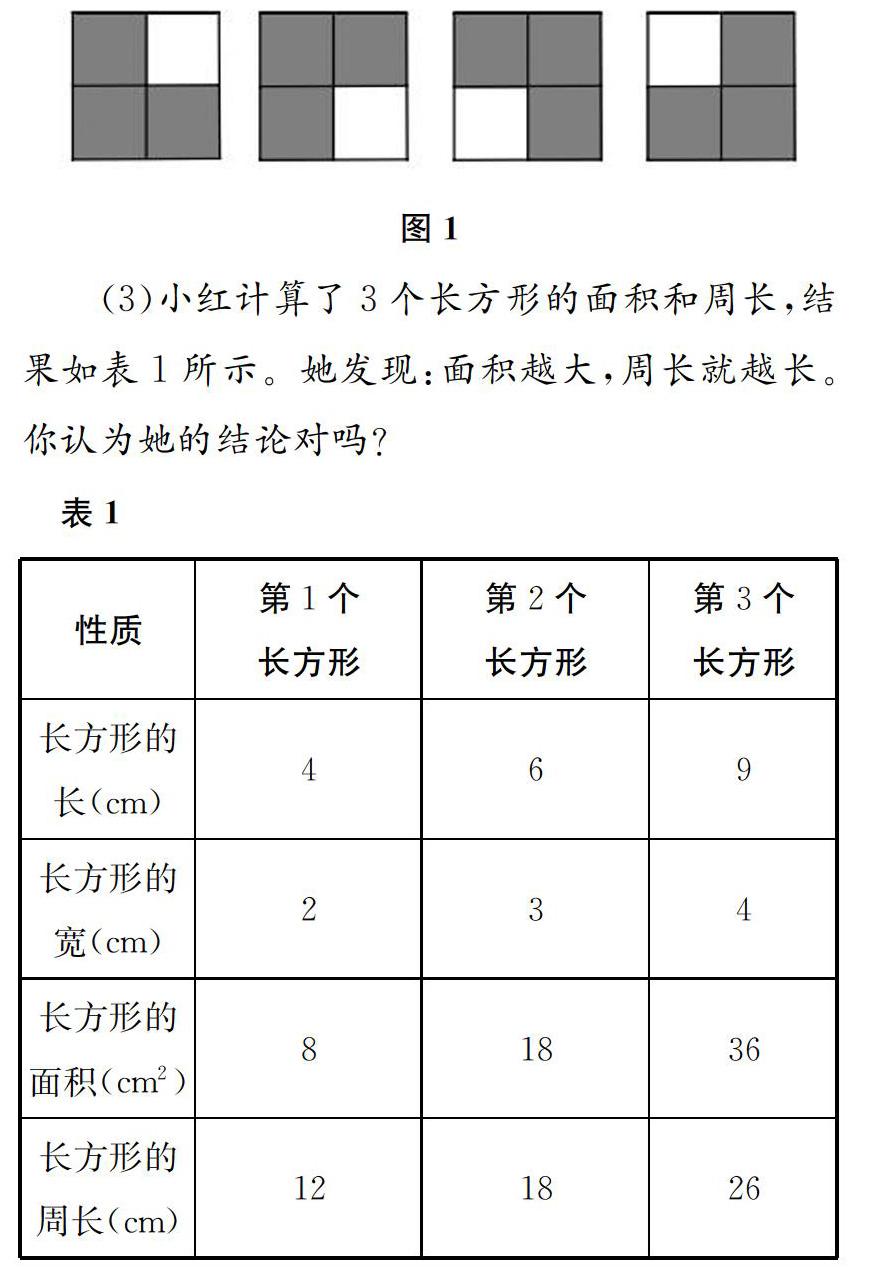
(2)图1中的4个图形有没有规律?如果你认为有规律,请说出规律。看谁发现的多。
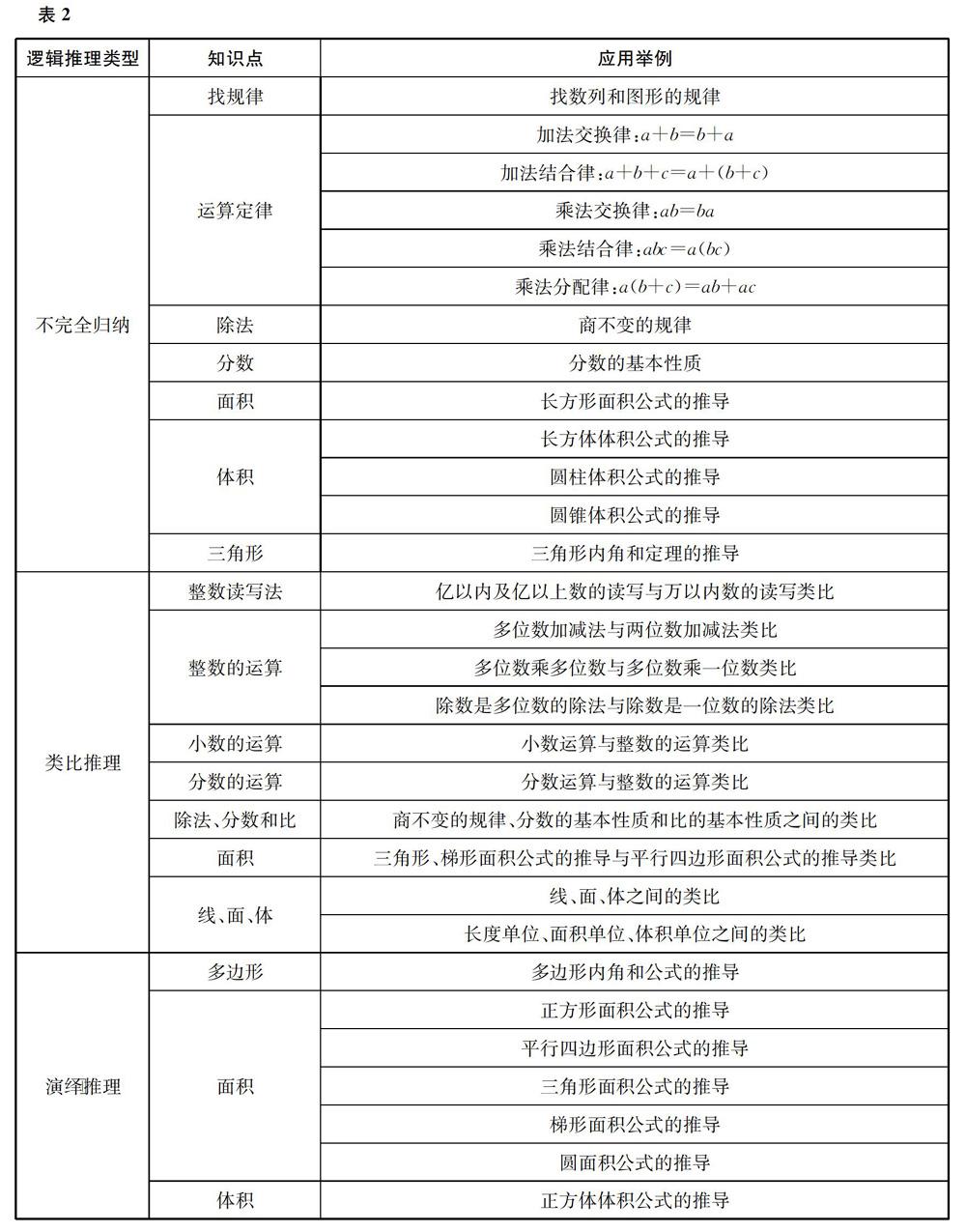
(3)小红计算了3个长方形的面积和周长,结果如表1所示。她发现:面积越大,周长就越长。你认为她的结论对吗?
第1题适合一年级的学生,引导他们通过简单的分析与比较,发现共同性与差异性,初步了解什么是规律,会做简单的分类。具体来说,可以按位数的多少、个位数是什么、十位数是什么及所含数字有哪些等标准(角度)来分类。
第2题适合二、三年级的学生,引导他们形成对规律的基本认识,提出一些简单的猜想,用自己的语言或数学语言加以表征。具体来说,这里的基本规律是各个图形都由四个小正方形组成,都是三个黑的、一个白的,白正方形的位置依次绕中心顺时针旋转90°。
第3题适合四、五年级的学生,引导他们通过错误猜想,懂得枚举归纳所得的结论具有或然性,从而明确检验的必要性,并用反例推翻错误猜想。具体来说,这里的结论是错的,可以举出反例:增加一个长方形,它的长、宽分别是8 cm、2 cm,面积是16 cm2,周长是20 cm,那么,表中第2个长方形面积比它的大,但是周长比它的小。
第4题适合六年级的学生,引导他们结合数的运算性质的学习,增加演绎成分,引进计算推证和科学归纳推理,从而通过个别事例的分析,发现因果关系,获得解释一般结论的内在根据。具体来说,这里的一般规律是相邻整数的最小公倍数是这两个数的积,其演绎推理的原因是相邻整数是互质的,其归纳推理的根据是3与4互质、4与5互质、6与7互质。
(二)结合知识经验,创设推理场景
在逻辑推理的训练中,教师没必要刻意给学生介绍逻辑知识,因为这些知识对学生来说显得比较抽象。实际上,学生可以通过多样化的实例潜移默化地掌握逻辑规则。
在小学阶段,学生的逻辑推理受到已有知识和经验的影响。如果推理内容超出了学生的数学知识和生活经验范围,那么,推理或者无法开展,或者产生错误。因此,对学生逻辑推理的训练既要注重在数学知识的教学中渗透,又要穿插一些与日常生活经验结合的实例。
例3(1)(可多选)下列说法正确的是()
A.所有的等边三角形都是等腰三角形
B.所有的等边三角形都不是等腰三角形
C.有些等边三角形是等腰三角形
D.有些等边三角形不是等腰三角形
(2)犯罪行為不是合法行为,故意杀人是犯罪行为。由此可以推出()
A.故意杀人不是合法行为
B.不合法行为是犯罪行为
C.不是犯罪行为一定合法
D.有的犯罪行为是合法行为
(3)所有的S都是P,有些M不是P。由此可以推出()
A.所有的M都是S
B.所有的M都不是S
C.有些M是S
D.有些M不是S
这里,第1题与数学知识相关,考查学生对直言三段论推理的四种格判断形式的掌握情况。第2题与数学知识无关,考查学生对日常生活中的直言三段论推理的理解。通过这类题,还可以给学生讲授一些法律知识,扩展他们的知识面。第3题是纯粹的逻辑问题,考查学生对直言三段论推理第二格的理解情况。
特别地,对归纳推理的训练,可以采用特殊化策略,即给出一般性问题,让学生在解答的过程中,先将其特殊化,再通过归纳推理解决一般情形。
教育研究与评论小学教育教学/2020年第12期前沿论坛例4(1)我们班一共有40位同学,如果每两位同学握一次手,那么一共握多少次手?
(2)平面上10条直线最多能将平面分割成多少个区域?
对于第1题,直接思考40位同学的情况过于困难,可以引导学生思考3位同学共握几次手,4位同学共握几次手,5位同学共握几次手……由简单到复杂发现一般的规律,通过归纳解决问题。同样地,对于第2题,直接思考10条直线的情况过于困难,可以引导学生思考1条直线最多分为1+1个区域,2条直线最多分为1+1+2个区域,3条直线最多分为1+1+2+3个区域,从而归纳出新增的第k+1条直线与原有的k条直线都相交,将平面多分割出k+1个区域,于是得到10条直线最多分为1+1+2+3+…+10=56个区域。
(三)梳理推理内容,把握培养时机
推理是数学思维的一般特征(方法),在很多知识的探究以及问题的解决中都会用到。而数学教学一般是按照知識点展开的,即以知识点为主题的。因此,教师要对教材中逻辑推理相关的知识内容加以梳理,做到心中有数,从而把握好训练学生逻辑推理的有效时机。表2列出了小学数学教材中逻辑推理相关的知识内容。表2
逻辑推理类型知识点应用举例不完全归纳找规律运算定律除法分数面积体积三角形找数列和图形的规律加法交换律:a+b=b+a加法结合律:a+b+c=a+(b+c)乘法交换律:ab=ba乘法结合律:abc=a(bc)乘法分配律:a(b+c)=ab+ac商不变的规律分数的基本性质长方形面积公式的推导长方体体积公式的推导圆柱体积公式的推导圆锥体积公式的推导三角形内角和定理的推导类比推理整数读写法亿以内及亿以上数的读写与万以内数的读写类比整数的运算多位数加减法与两位数加减法类比多位数乘多位数与多位数乘一位数类比除数是多位数的除法与除数是一位数的除法类比小数的运算小数运算与整数的运算类比分数的运算分数运算与整数的运算类比除法、分数和比商不变的规律、分数的基本性质和比的基本性质之间的类比面积三角形、梯形面积公式的推导与平行四边形面积公式的推导类比线、面、体线、面、体之间的类比长度单位、面积单位、体积单位之间的类比演绎推理多边形面积体积多边形内角和公式的推导正方形面积公式的推导平行四边形面积公式的推导三角形面积公式的推导梯形面积公式的推导圆面积公式的推导正方体体积公式的推导这里需要强调一点,现行教材把运算律安排在四年级,有点晚了;运算律应当从二年级开始就逐步引入,这对于发展学生的逻辑推理能力有举足轻重的作用。
参考文献:
[1] 方富熹,方格,朱莉琪.“如果P,那么Q……?” ——儿童充分条件假言演绎推理能力发展初探[J].心理学报,1999(3).
[2] 李丹,张福娟,金瑜.儿童演绎推理特点再探——假言推理[J].心理科学通讯,1985(1).
[3] 吴荣先.儿童选言推理能力发展特点初探[J].心理学探新,1989(4).
[4] 林崇德,沃建中,陈浩莺.小学生图形推理策略发展特点的研究[J].心理科学,2003(1).
[5] 方富熹,唐洪,刘彭芝.12岁儿童充分条件假言推理能力发展的个体差异研究[J].心理学报,2000(3).
[6] 李国榕,胡竹菁.中学生直言性质三段论推理能力发展的调查研究[J].心理科学通讯,1986(6).
[7] 沃建中,林崇德,陈浩莺,等.小学生图形推理策略个体差异[J].心理发展与教育,2003(2).
[8] 林崇德.学习与发展:中小学生心理能力发展与培养(修订版)[M].北京:北京师范大学出版社,2003.
[9] 倪斯杰,张君达.小学二年级学生数学能力的分析[J].心理发展与教育,1998(1).
[10] Csapó,B. The Development of Inductive Reasoning:Crosssectional Assessments in an Educational Context[J].International Journal of Behavioral Development,1997(4).
[11] 费广洪,王淑娟.3~11岁儿童类比推理发展的研究[J].心理学探新,2014(6).
[12] Sloutsky,V.M.,Fisher,A.V.Linguistic labels:Conceptual markers or object features?[J].Journal of Experimental Child Psychology,2012(1).
[13] Rehder,B.,Colner,R.M.,Hoffman,A.B.Feature inference learning and eyetracking[J].Journal of Memory and Language,2009(3).
[14] 孙红梅,孙小越,阴国恩.小学生归纳推理能力的发展研究及培养策略[J].天津市教科院学报,2019(6).
[15] 王树芳,莫雷,金花.任务难度和反馈学习对儿童类比推理能力的影响[J].心理发展与教育,2010(1).
[16] 胡卫平,刘佳.小学生思维能力的培养:五年追踪研究[J].心理与行为研究,2015(5).
[17] 陈德煜,李根娣,程卫.小学三年级数学思维能力训练报告[J].上海教育科研,1985(4).
[18] 王瑾.小学数学课程中归纳推理的理论与实践研究[D].长春:东北师范大学,2011.热点透视
