基于半忘期的双相学习—遗忘生产—库存优化

伏开放 （广东金融学院 工商管理学院，广东 广州 510521）

员工具有的学习效应可以实现人力资本的增值，但学习效应建立在连续工作的基础上。当工作中断后，会导致学习中断，中断发生后员工对原先掌握的学习经验就会遗忘，遗忘会造成知识损耗。当进行生产—中断的往复循环时，对学习与遗忘的研究有助于分析劳动技能培训与巩固、短期雇佣与长期雇佣等对员工生产率的影响。

关于学习效应的研究，以往学者大多忽视了员工的认知学习过程，或者干脆将认知学习过程与技能学习过程整合在一起，使得所建立的学习曲线不能准确地反映真实情况。所谓认知学习是指人在认知过程中的学习，认知学习主要是一个信息交换过程，在信息交换过程中通过感知、注意、记忆和理解等方式获取信息。技能学习是指个体在操作过程中的学习，由于技能学习的存在操作者熟练程度越来越高。

著名学者Jaber对学习曲线和遗忘曲线的研究做出了突出的贡献。Jaber和Bonney[1]较早建立了学习—遗忘曲线模型（LFCM），并将该模型应用到了Salameh等[2]的模型中，求解了学习—遗忘下不同周期的最优生产量。对于学习效应和遗忘效应，多数学者聚焦在学习效应，也有少数研究员工作业行为具有学习效应和遗忘效应的生产库存模型。Jaber和Bonney[3]将Jaber和Kher[4]提出的双相学习遗忘曲线应用到了Economic Manufacture Quantity（EMQ）模型中，研究表明当忽略认知学习或技能学习时，在计算成本时会有较大的误差。其他关于遗忘效应行为在EPQ模型中的应用包括：Jaber等[5]、Jaber等[6]、Kazemi等[7]。

关于认知学习与技能学习，Dar-EL等[8]通过分析大量的心理学和工业实践方面的文献认为虽然WLC整合了学习过程中的认知因素和技能因素，但是WLC模型没有区分认知和技能学习。针对这个局限性，他们提出了双重（也叫双阶段）学习曲线模型，第1阶段为认知学习，第2阶段为技能学习。Jaber和Glock通过对初始生产时间的划分，改进了Dar-EL等人的模型，同时通过对大量的数据进行模拟分析，发现改进后的学习曲线更贴合实际情形。

员工遗忘效应行为在生产—库存系统中应用包括：Chiu and Chen[9]考虑生产过程及生产准备过程中存在的学习效应和遗忘效应，假设遗忘率为常数，构建了供货时间间隔相同、供货数量不同的多维动态规划生产—库存优化模型。Glock和Jaber[10]构建了两级生产—库存优化系统，分析了不同的学习和遗忘参数对生产率的影响，并着重探讨了员工学习是如何转移生产的瓶颈的。Khan等（2014）[11]将学习效应拓展到Huang（2004）[12]的模型中，将学习效应应用到了经典两级生产—库存模型中。

本文的研究建立在已有关于学习和遗忘的研究基础上，对现有关于学习和遗忘的研究进行了更深入地拓展，建立了基于半忘期的学习—遗忘曲线以及基于半忘期的双相学习—遗忘曲线，并将所建立的曲线应用到了两级生产—库存优化模型中。

1 基于半忘期的学习—遗忘曲线

由艾宾浩斯的遗忘曲线理论得知，遗忘在学习之后立即开始，而且遗忘的进程并不是均匀的。最初遗忘的快，后期遗忘的慢。放射性元素的衰减过程也是遵循最先衰减的快、后期衰减的慢的规律。本节基于放射性元素的衰减规律提出基于半忘期的学习—遗忘理论。

设τ为员工遗忘一半知识或技能所需要的时间，也即半忘期。半忘期越小表明遗忘的越快。Ni为第i个周期经过作业中断后保存的经验数，令N0=0，T1i为第i个周期完成第一件产品的生产时间。员工在作业过程中存在学习特征，学习规律遵循Wright学习曲线模型。当作业生产中断后，学习效应不能继续保持，发生遗忘，经过中断时间tsi后，保留的经验数为：

式（1）中：Ni-1为第i-1个周期经过中断后保存的经验数，q为当期完成的作业量。可得第i+1个周期完成第一件产品的生产时间为：

2 基于半忘期的双相学习—遗忘曲线

员工作业行为具有的学习特征包括认知学习和技能学习[14]，基于此，作者认为在遗忘的过程中也存在认知遗忘和技能遗忘，遗忘的规律遵从前节描述的规律，因在遗忘过程中存在两类遗忘，故称为双相遗忘。

当作业生产中断后，员工作业行为具有的认知学习不能继续保持，发生认知遗忘，经过中断时间tsi后，保留的认知经验数为：

式（3） 中：为第i-1个周期经过中断后保存的认知经验数，q为当期完成的作业量，τc为认知半忘期。当生产中断后，技能学习不能继续保持，发生技能遗忘，经过中断时间tsi后，保留的技能经验数为：

式（4） 中：为第i-1个周期经过中断后保存的认知经验数，τm为技能半忘期。在经历认知遗忘和技能遗忘的双相遗忘后，第i+1个周期完成第一件产品所需的生产时间为：

据统计，“十二五”期间，我国由公路建设引起的地表扰动破坏总面积为119.6万公顷，占开发建设项目干扰总面积的21.6%。其中，山地、丘陵地区75.3万公顷，占公路干扰破坏总面积的62.97%。且山地丘陵区自然条件较差，一旦被破坏，极难被恢复。

式（5）中：β为认知学习所占第一件产品的生产时间比例，1-β表示技能学习所占第一件产品的生产时间比例。

3 供应商—制造商联合成本

本文研究的生产库存系统由一个供应商与一个制造商构成，当员工作业行为具有学习和遗忘特征时，参照伏开放等（2019）的研究可得第i周期内集成生产—库存系统的平均成本为：

式（6） 中：n为一个周期内供货次数，Q为一个周期内单次供货量，As为供应商生产准备成本（元/次），c为供应商单位时间生产成本（元/天），Ti1为供应商第i周期生产第一件产品的时间（天），T为供应商连续两次供货的时间间隔（天），hs为供应商单位产品存储成本（元/单位/天），l为供应商学习系数，Am为制造商订购成本（元/次），F为制造商承担的固定运输成本（元/次），hm1为粗加工产品在制造商处的单位存储成本（元/单位/天），hm2为精加工产品在制造商处的单位存储成本（元/单位/天），θ为制造商单位产品的精加工费用（元/单位）。

采用文献[15]中给出的算法求解n和Q。

4 算例分析

出于商业保密，数据采用模拟数据。设l=1 000（元/年），c=1 000（元/年），hs=2（元/单位/年），hm1=2.2（元/单位/天），hm2=2.8（元/单位/天），As=300（元/次），Am=100（元/次），D=12（单位/天），F=25（元/次），T11=0.0625（天），θ=0.5（元/单位）。

4.1 基于半忘期学习—遗忘理论的生产—库存算例分析

参照伏开放等（2019）给出的算法，当n=11，Q=12时，集成生产—库存系统在第一个生产周期的成本最小。当τ=2.5时，在第一个生产周期内，供应商粗加工132件产品的时间为T（ 132）=（0.0625/（1-0.3 2））×1321-0.32=2.5131天，作业中断时间nT-T1p=11×1-2.5131=8.4869，在已粗加工132件的前提下，经过作业中断产生遗忘后，第一个生产周期的累积经验数为N1=132×0.5（8.4869/2.5）≈13。在第二个作业生产周期完成第一件产品的生产时间为T12=0.0625×（13+1 ）-0.32=0.0269，粗加工91件产品的时间为T（ 91）=0.0269/（1-0.32 ）×911-0.32=0.8499天，作业中断时间nT-T2p=7×1-0.8499=6.1501，经过作业中断产生遗忘后，第二个生产周期的累积经验数为N2=104×0.5（6.15 01/2.5）≈19。在第三个生产周期完成第一件产品的生产时间为T13=0.0625（ 19+ 1 ）-0.32=0.024。其他依次类推。表1呈现了不同半忘期下不同周期的最优解。在半忘期遗忘理论下，不论半忘期取何值，平均成本在后期不会出现波浪式的摇摆。

表1 不同半忘期下的最优解

当τ→∞时，也即遗忘不存在时，平均成本随着生产的进行表现出逐步缓慢递减的规律。由表1知，当τ=1.5时，从第二个生产周期开始，作业中断后员工具有的遗忘效应使得前期累积的经验数完全遗忘。遗忘效应的存在使得学习效应不能发挥作用，从而平均成本保持不变。遗忘情形相比于无遗忘情形，遗忘情形下生产更早趋于稳定，平均成本也更高。

图1呈现了第二个生产周期内不同半忘期对最优成本的影响。当τ＜1和τ＞3时，系统平均成本对半忘期的变化是不敏感的，当τ＜1时，由于遗忘的太快，作业中断使得前期累积的学习经验数一点不能保留，所以系统平均成本基本不变，对半忘期的变化不敏感。当τ＞3时，遗忘的较慢，作业中断对学习效应的弱化非常有限。当1＜τ＜3时，系统平均成本对半忘期的变化是非常敏感的，此阶段的半忘期对成本影响显著，管理者应通过培训等方法延长半忘期，从而削弱作业中断对学习效应的弱化作用。当τ＞5时，系统平均成本对半忘期的变化是非常不敏感的，此时再通过增加投入来延长半忘期，以期来降低成本是不明智的。

图1 半忘期学习—遗忘理论下半忘期变化对最优成本的影响

4.2 基于半忘期双相学习—遗忘理论的生产—库存算例分析

对于学习系数，取认知学习率φc=70%，技能学习率φm=90%，即学习系数为：bc=0.514、bm=0.152，h=3.605，β=78.28%。根据公式可得b=0.337。表2呈现了当τc=1.8，τm=2.3时的最优解。

在第一个周期的总生产量为132，经过作业中断后，员工保留的认知经验数为5，技能经验数为10，认知经验数少于技能经验数是因为认知半忘期小于技能半忘期，相比于技能遗忘，认知遗忘更快。员工作业行为具有的认知学习遗忘和技能学习遗忘特征，综合影响下使得第三个生产周期后，最优的供货次数和最优单次供货量保持不变。随着认知与技能学习—遗忘—学习—遗忘的重复，系统的平均成本在作业的后期出现了摇摆。这与非双相学习—遗忘理论下情形不同。

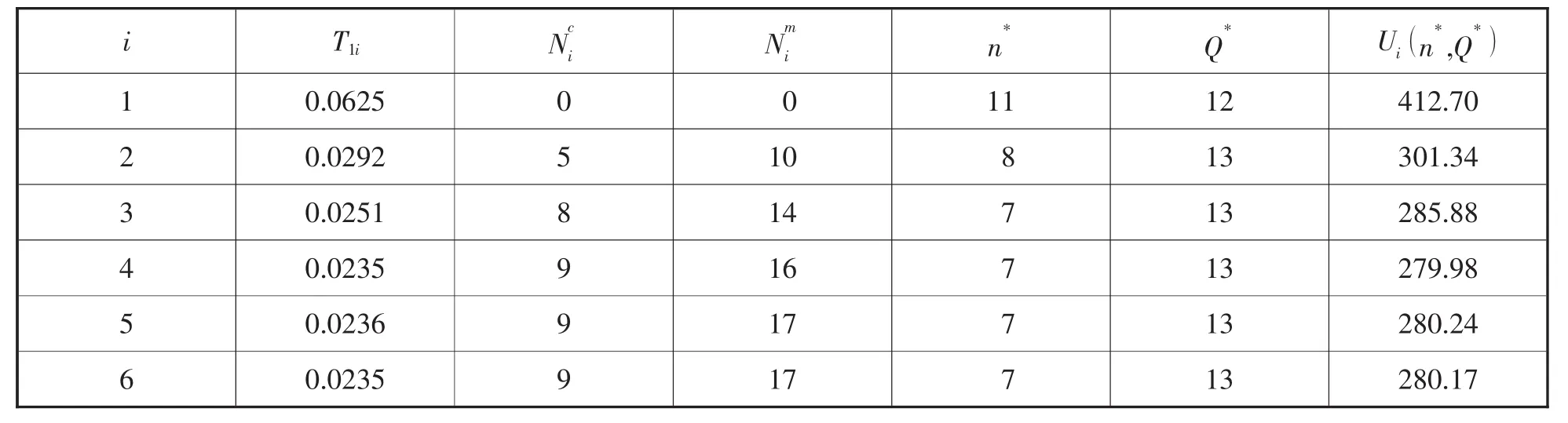
表2 不同生产周期下基于双相学习—遗忘理论下的最优解

图2呈现了第二个生产周期内认知半忘期与技能半忘期变化对最优成本的影响。由于认知学习时间与技能学习时间所占生产生产时间的比例不同，导致认知遗忘与技能遗忘对系统平均成本的影响不同。τc相比于τm，τc给系统平均成本带来的影响幅度要大。

当τm=2.3时，观察认知半忘期变化对系统平均成本的影响。根据计算得知，当τc＜0.6或τc＞6时，系统平均成本对认知半忘期的变化不敏感。当τc＞1时，认知半忘期对系统平均成本的影响呈现双曲线变化特征。当1＜τc＜6时，系统平均成本对认知半忘期的变化比较敏感，当作业中断后，管理者应采取措施，延长认知半忘期，达到降低成本的目的。

当τc=1.8时，观察技能半忘期变化对系统平均成本的影响。根据计算得知，当τm＜0.8或τm＞4时，系统平均成本对技能半忘期的变化不敏感。当1＜τm＜4时，系统平均成本对认知半忘期的变化比较敏感。管理者在敏感期内延长技能半忘期，达到降低成本的目的。

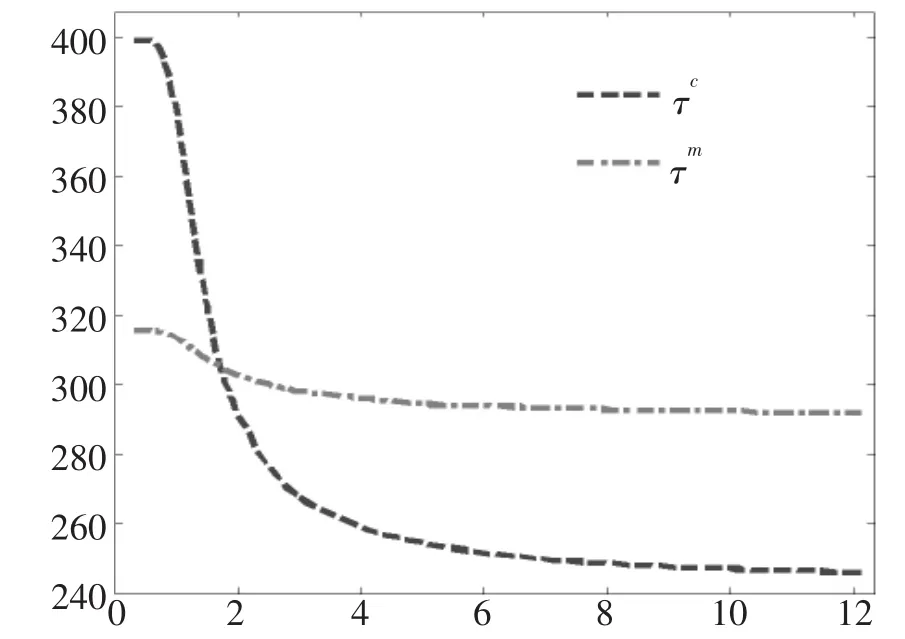
图2 不同认知半忘期与技能半忘期变化对最优成本的影响

5 结束语

本文探讨了当员工作业行为具有学习和遗忘特征时，如何决策最优的单次供货量和供货次数使得系统平均成本最低。提出了基于半忘期的学习—遗忘理论和基于半忘期的双相学习—遗忘理论，并将所提出的两种学习—遗忘理论应用到两级生产—库存模型中。所得到的结论主要包括：

（1）当半忘期趋向无穷大时，也即遗忘不存在时，平均成本随着生产的进行表现出早期迅速减少，后期缓慢减少的特征。当半忘期时间较短时，作业中断使得前期累积的学习经验全部遗忘，完全遗忘的存在使得学习效应对成本发挥的降低作用有限。不同半忘期的调整对成本的降低作用显著不同。

（2）相比于非双相学习—遗忘理论下的成本变化，在双相学习—遗忘理论下，随着认知与技能学习—遗忘—学习—遗忘的重复，系统的平均成本在作业的后期出现了摇摆，而非双相学习-遗忘理论情形下，没有出现成本的摇摆特性。遗忘情形相比于无遗忘情形，遗忘情形下生产更早趋于稳定，平均成本也更高。

（3）遗忘的越快，平均成本越高，管理者应尽可能压缩作业中断时间，当作业中断时间不能压缩时，在作业中断时间内展开培训或者将员工调整到相似的工作岗位，延缓遗忘效应，从而减少遗忘带来的损失。相比于压缩技能半忘期，压缩认知半忘期带来的成本减少作用更明显。

生产管理者应当生产中断期间，采取培训等措施对员工的生产技能进行巩固，防止员工在中断期间遗忘全部或部分之前累积的生产经验，防止中断导致学习的知识丢失。倘若生产停止后不采取措施，任由员工经验的丢失，当生产恢复时，员工需要较长的生产时间才能恢复到生产中断前的水平，这也将导致生产成本的增加。