小样本条件下基于Bayes方法的装备状态评估

谷广宇 刘建敏 乔新勇

摘要：  针对小样本条件下单纯采用使用期无法准确衡量装甲装备技术状况的问题，本文以装甲车辆发动机状态评估为例，分析了小样本条件下，装备各技术状况等级特征参数分布及其有效性和适用性。同时，采用Bayes决策法，从装备属于各技术状况等级的概率和错判风险两方面出发，对装备状态进行评估。评估结果表明，利用两种Bayes方法均能准确评估发动机技术状况，评估准确率达90%以上，并且基于最小风险的Bayes评估方法具有更好评估效果，评估准确率较高，符合装甲车辆技术状况随使用时间增加而逐渐变差的一般规律。该方法在装备状态评估中具有实用性及可行性。

关键词：  状态评估; 小样本; Bayes决策法; 发动机

中图分类号： TK428; E923.1 文獻标识码： A

收稿日期： 2019-03-25; 修回日期： 2019-06-27

基金项目：  国家自然科学基金资助项目（U1836101）

作者简介：  谷广宇（1989-），男，汉族，博士研究生，主要研究方向为发动机状态评估与预测。

装甲装备在使用过程中，其技术状况将随着使用时间的增长发生变化，且呈现劣化趋势。虽然其技术状况在一定程度上可以采用运行时间来衡量[1]，但由于使用环境、使用强度及工作地点等因素不尽相同，该方法有时不能完全真实地反映装备的实际技术状况。因此，需要运用科学的方法对装甲装备进行技术状况评估[2]。通常情况下，在装备的状态检测评估过程中，首先要采集装备状态信息，并对数据样本进行统计分析，才能得到相关结论。目前，基于数据驱动的评估方法主要有模糊聚类[3]、支持向量机[4]、神经网络[5]、Bayes决策法[6]等。这些方法就统计分析而言，均需要尽可能大的样本量，然而在实际评估过程中，受试验成本、试验周期等条件影响，无法进行大量试验来获取大样本。在此情况下，仍采用传统大样本条件下的统计方法，难以保证其最终得到评估结果的可靠性。因此，研究在小样本条件下的状态检测评估方法具有实际意义[7]。另外由于在状态信息采集测量过程中，用以描述各个技术状况的特征参数都是随机变量，同一技术状况下所有采集测量的样本只可能是相似的，不可能完全一样，而且某一特征值可能不只出现在某一特定状况下，在其他状况中也可能出现。鉴于Bayes决策理论既能参考各类状态的分类错误率，又能考虑分类错误的风险程度，具有较强的分类决策能力。因此，本文采用Bayes决策法对装备技术状况进行评估，并利用小样本统计方法构造各技术状况下特征参数的分布，以获取Bayes决策中的类条件概率密度。该研究可以对即将变“差”的车辆提前进行预防性维修，降低故障风险。

1 小样本统计原理与方法

为提高统计分析精度，在小样本条件下，最有效的解决方法是设法增加信息量。在此类方法中，以美国斯坦福大学B.Efron教授提出的Bootstrap法[8]及B.R.Donald提出的Bayes Bootstrap法[9]最为简单有效，而且在工程应用中取得了丰硕成果[10-13]。其基本思路都是依据现有小样本模仿未知分布，进而获取再生样本，将小样本问题转化成大样本。因此，该方法适用于本文对不同技术状况下小样本状态信息的统计分析。

1.1 Bootstrap方法

Bootstrap方法又称自助估计法，其原理主要根据观测到来自于未知总体分布F的随机子样X=（X1，…，Xn），估计总体分布F的某一分布特征R（X，F），如均值、方差等，从而推测总体分布F。具体方法如下：

设总体分布F的某个分布特征θ=θ（F）（如均值，方差等），由观测子样X=（X1，…，Xn）构造经验分布Fn，则有对θ的估计=（Fn），估计误差为

Tn=（Fn）-（F）（1）

根据经验分布Fn，重新抽取再生子样X（1）=（X（1）1，…，X（1）n），进而构造经验分布函数F（1）n。于是由X（1）又可得到θ的估计（F（1）n）。此时，可得到估计误差Tn的Bootstrap统计量R（1）n，即

R（1）n=（F（1）n）-（Fn）（2）

重复抽取多组再生子样X（i），i=1，2，…，m，可计算相应R（i）n，i=1，2，…，m，并利用R（i）n的分布去逼近Tn的分布，并根据式（1）得到θ（F）的样本，即

θ（i）（F）=（Fn）-Tn≌（Fn）-R（i）n（3）

该方法与传统统计方法相比，在小样本估计中具有较高精度。

1.2 Bayes Bootstrap方法

Bayes Bootstrap方法，即随机加权自助法，也是将子样信息“提携”的方法，是对Bootstrap方法的改进。其原理主要利用Dirichilet随机向量对子样X=（X1，…，Xn）进行加权，从而计算随机加权统计量Dn，进而利用Dn模仿估计误差Tn的分布。具体方法如下：

设子样X=（X1，…，Xn）来自于未知总体分布F，μ和σ2为F的未知期望和方差，和S2为X的统计期望和方差，则估计误差为

T1=-μ（4）

T2=nn-1S2-σ2（5）

式中，T1和T2为期望的估计误差和方差的估计误差。生成N个参数为（1，…，1）的Dirichilet随机向量Vi=（vi1，vi2，…，vin），i=1，2，…，N，可获取随机加权统计量为

Di1=∑nk=1vikxk-（6）

Di2=nn-1∑nk=1vik（xk-）2-nn-1S2（7）

利用Di1和Di2模仿估计误差T1和T2的分布，根据式（4）和式（5），可得

μ=-T1≈-1（8）

S2=nn-1S2-T1≈nn-1S2-2（9）

已有成果的实际应用及仿真计算表明，该方法分析精度较高于Bootstrap方法[14]。

2 Bayes决策理论

Bayes决策理论是模式识别问题中经典的分类决策理论，其基本思想是通过各状态下的先验概率分布推定后验概率[15]。根据决策规则，Bayes决策又分为基于最小错误率[16]和基于最小风险的Bayes决策[17]。

2.1 基于最小错误率的贝叶斯决策

假设共有m个决策状态总体W=（w1，w2，…，wm），已知其先验概率P（wi），i=1，2，…，m，依据前文小样本统计理论可推定各状态下特征参数x的分布模型，并获得其类条件概率密度P（x|wi）。则根据Bayes公式，可得各状态后验概率为

P（wi|x）=P（x|wi）P（wi）∑mi=1P（x|wi）P（wi）（10）

并有决策规则：若P（wi|x）=max＼[P（wi|x）＼]，则x∈wi。此类决策规则称为基于最小错误率的贝叶斯决策。

2.2 基于最小风险的贝叶斯决策

实际决策过程中除了错误率外，有时也需要考虑决策错误所带来的风险，在这种情况下，通常可以选择基于最小风险的贝叶斯决策方法[18]。

基于最小风险的贝叶斯方法在基于最小错误方法上引入了“损失”的概念，即把属于wi的状态错判为aj状态的损失，可记为cji，一般决策损失表如表1所示。

根据表1及前文所得后验概率，可计算决策为wi的状态条件风险为

R（wi|x）=E＼[c（i|j）＼]=∑mj=1c（j|i）P（wj|x）（11）

并有决策规则：若R（wi|x）=min＼[R（wi|x）＼]，则x∈wi。

3 应用实例

基于贝叶斯方法的装备状态评估，实质上就是将装备的技术状况划分为从优到劣几个等级的问题，本文以装甲车辆发动机状态评估为例，并依据摩托小时（使用时间）将其技术状况分为“优”、“良”、“一般”、“较差”、“差”这5个等级，分别以“0～200”，“200～300”，“300～400”，“400～500”，“500～600”这5个阶段统计特征表示，即有W=（w1，w2，w3，w4，w5）={“优”，“良”，“一般”，“较差”，“差”}。

3.1 特征提取

評估发动机技术状况的参数很多，但实践证明，通过减速时间评估技术状况是一种简单有效的办法[19]，因此本文选取柴油机减速时间作为技术状况评估的特征参数。减速时间是指发动机在最高空转转速下运转时迅速停止供油，使其自行减速，计算从最高空转转速减到转速为0的时间。随着使用时间增长，发动机活塞缸套磨损增加，阻力减小，减速时间将变长[20]。

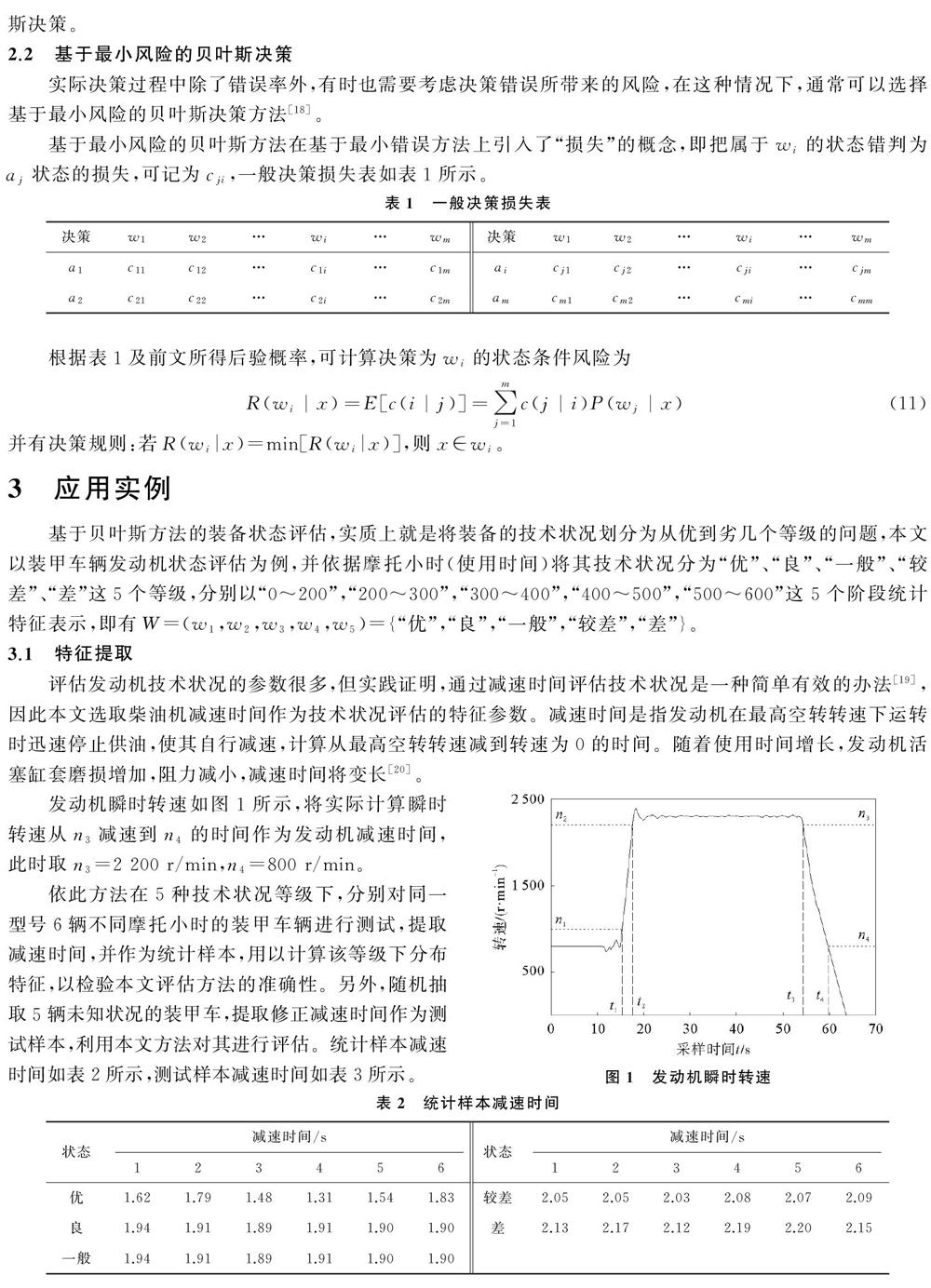
发动机瞬时转速如图1所示，将实际计算瞬时转速从n3减速到n4的时间作为发动机减速时间，此时取n3=2 200 r/min，n4=800 r/min。

依此方法在5种技术状况等级下，分别对同一型号6辆不同摩托小时的装甲车辆进行测试，提取减速时间，并作为统计样本，用以计算该等级下分布特征，以检验本文评估方法的准确性。另外，随机抽取5辆未知状况的装甲车，提取修正减速时间作为测试样本，利用本文方法对其进行评估。统计样本减速时间如表2所示，测试样本减速时间如表3所示。

3.2 小样本统计

假设发动机减速时间在各个使用阶段均服从正态分布，利用Bayes Bootstrap小样本统计方法，对各个阶段减速时间进行统计，根据式（4）～式（9），得各阶段分布的均值和标准差，Bayes Bootstrap法下各技术状况分布特征如表4所示，各技术状况等级分布特征如图2所示。由表4和图2可以看出，减速时间随技术状况等级变化较为明显，因此能够较好地反映发动机技术状况的变化。

3.3 基于Bayes决策的状态评估

由于测试车辆摩托小时在0～600 h内呈均匀分布，因此各状态的先验概率为

P（W）=＼[1/3，1/6，1/6，1/6，1/6＼]

考虑评估过程中错误率的存在，根据经验，引入发动机状态评估决策损失C，发动机状态评估决策损失如表5所示。

3.4 评估准确性对比

根据表4及式（10）和式（11），分别利用两种Bayes方法对统计样本进行评估，统计样本评估结果如表6所示。

由表6可以看出，利用两种Bayes方法均能够准确评估发动机技术状况，评估准确率达90%以上，并且基于最小风险的Bayes评估方法具有更好评估效果。

3.5 测试样本状态评估

采用基于最小风险的Bayes评估方法，对表3测试样本进行评估，在5种状态下，各测试样本的条件风险及评估结果如表7所示。

由表7可以看出，评估结果符合装甲车辆技术状况随使用时间增加而逐渐变差的一般规律，证明该方法在装备状态评估中的实用性及可行性。

该方法还能判断测试样本的变化趋势，例如测试样本1根据表7被评估为“优”状态，但其“良”状态的风险与“优”状态只有很小差别。因此，可判断该样本接近“优”状态与“良”状态的边缘，即将退化为“良”状态。依据该方法可以对即将变“差”的车辆提前进行预防性维修，以降低故障风险。

4 结束语

本文通过结合Bootstrap小子样统计方法及Bayes决策法，有效地解决了小样本条件下的装甲装备状态评估的问题，并以装甲车辆发动机为例，验证了该方法的有效性。采用Bootstrap小子样统计方法，能够有效扩充发动机状态参数样本，实现小样本条件下的装备状态评估的先验统计;Bayes决策法在装备状态评估过程中，不但考虑了各技术状况出现的概率，还考虑了错误评估的风险，比其他技术状况评估方法更具合理性;采用本文方法进行装甲车辆发动机的技术状况等级评估，评估结果较符合实际规律，正确率可达90%以上。该研究具有一定工程实用性及可行性。

参考文献：

[1] 李国锦. 基于层次分析及模糊综合评判的装甲车辆发动机状态评估[J]. 车辆与动力技术， 2017（4）： 40-44.

[2] 张会奇， 陈春良， 刘峻岩， 等. 基于BP神经网络的装甲车辆发动机使用状态评价[J]. 兵工自动化， 2014， 33（1）： 32-34.

[3] 辛江慧， 邹政耀， 任成龙.  基于灰色定权聚类的混合动力汽车发动机运行状态评估[J].  重庆理工大学学报：自然科学， 2014， 28（7）： 26-29.

[4] 汪瑾， 陈果， 王洪伟， 等.  基于后验概率SVM的航空发动机滚动轴承状态评估[J].  轴承， 2015（5）： 55-59.

[5] 刘伯运， 欧阳光耀， 常汉宝.  基于神经网络和DS证据理论的柴油机状态评估[J].  车用发动机， 2005（5）： 14-17.

[6] 朱伟明.  基于贝叶斯融合的柴油机性能状态评估方法研究[J].  内燃机， 2010（2）： 18-19， 36.

[7] 高攀东， 陈晓阳， 沈雪瑾， 等.  小样本下轴承可靠性评估方法对比分析[J].  轴承， 2014（12）：  44-48.

[8] Efron B， Tibshirani R J.  An introduction to the bootstrap[M].  London： Chapman and Hall， 1993.

[9] Donald B R.  The bayesian bootstrap[J].  The Annals of Statistics， 1981， 9（1）： 130-134.

[10] 李会鹏， 明廷锋， 贺国.  小样本条件下一种旋转机械振动状态阈值的确定方法及应用[J].  武汉理工大学学报： 交通科学与工程版， 2012， 36（5）： 1059-1063.

[11] 乔新勇， 刘建敏， 张小明.  小子样统计理论在装备状态检测中的应用[J].  装甲兵工程学院学报， 2009， 23（2）： 41-43， 87.

[12] 唐雪梅， 周伯昭， 李荣.  武器装备小子样综合试验设计与鉴定技术[J].  战术导弹技术， 2007（2）： 51-56， 79.

[13] 袁 鹏， 张卫兵， 韩自刚. 银川地区建筑地基沉降计算验系数取值[J]. 科学技术與工程， 2017， 17（20）：  236-240.

[14] 樊鹤红， 刘盼， 赵兴群， 等.  小样本条件下行波管可靠性评估方法的研究[J].  电子学报， 2010， 38（6）： 1394-1398.

[15] 张湘平， 张金槐， 谢红卫， 等.  基于随机加权法的BAYES精度评定[J].  国防科技大学学报， 2001， 23（3）： 98-102.

[16] 全星慧， 牟海維， 吕秀丽， 等.  基于PCA与贝叶斯决策的人脸识别算法[J]. 光学仪器， 2014， 36（2）： 122-125.

[17] 徐智康， 李旸， 李德玉. 基于可变最小贝叶斯风险的层次多标签分类方法[J]. 南京大学学报： 自然科学版， 2017， 53（6）： 1023-1032.

[18] 毛思敏.  基于最小风险贝叶斯准则的工业过程故障诊断[D]. 武汉：华中科技大学， 2016.

[19] 张更云， 何来龙.  一种评价发动机实际技术状况的方法[J].  装甲兵工程学院学报， 2005， 19（4）： 67-70.

[20] 张小明， 刘建敏， 乔新勇， 等. 柴油机健康状况评估及其方法[J]. 装甲兵工程学院学报， 2008， 22（2）： 30-34.

Equipment States Evaluation Based on Bayes Method with Small Sample

GU Guangyu， LIU Jianmin， QIAO Xinyong

（Vehicle Engineering Department， Army Academy of Armored Forces， Beijing 100072， China）

Abstract：  In order to solve the problem that the technical condition of armored equipment can not be accurately measured by using the service life alone under the condition of small sample， this paper takes the engine state evaluation of armored vehicle as an example， and analyzes the effectiveness and applicability of the characteristic parameters distribution in each technical condition of the equipment under the condition of small sample.  At the same time， the Bayes decision method is used to evaluate the equipment status from two aspects：  the probability of the equipment belonging to each technical condition grade and the misjudgment risk.  The evaluation results show that both Bayes methods can accurately evaluate the engine technical status， and the evaluation accuracy is larger than 90%.  The Bayes evaluation method based on minimum risk has better evaluation effect and higher evaluation accuracy， which accords with the general law that the technical condition of armored vehicles becomes worse with the increase of service time.  This method is practical and feasible in equipment condition evaluation.

Key words：  states evaluation; small sample; Bayes decision; engine