圆柱端面上正弦曲线在数控铣削中的编程探究

年得君 余正存

摘要：通过分析了正弦曲线在数控铣床上的加工难点，经过多次试验，试验表明，优先选用宏程序编制圆环上正选曲线的编程方法，不仅程序准确性高、占有机床内存小，而且便于修改，从而对提高加工效率与加工精度有极大的帮助。其方法是用圆参数方程中的变量和正弦曲线中的变量关系，将复杂的曲线用很多小直线来代替，逐步逼近曲线的轮廓，从而编制出加工圆台上正弦曲线的宏程序完成加工。此方法对非圆曲线的零件轮廓程序编制提供了一定的依据，通用性好，具有推广意义。

关键字：正弦曲线;宏程序;数控铣床

中图分类号： TG547     文献标志码：A

0引言

对于数控加工而言，影响零件的加工效率与加工质量因素，除了刀具选择、工艺安排等之外，数控编程是数控加工的主要环节。数控编程有两种方法，手工编程与软件编程，软件编程就是利用计算机CAD/CAM软件来编程加工，但是计算机编程产生的空刀运行比较多，程序也比较长，机床占有内存大，如遇问题不易检查修改等缺点，反而加工时间较长工作效率不高。手工编程是软件编程的基础，编制简洁，程序量较小等优点，本文以图1为例，采用FANUC0i数控系统，从加工工艺设计、刀具选择、编程方法等研究了该零件的加工。

加工工艺安排及刀具选择

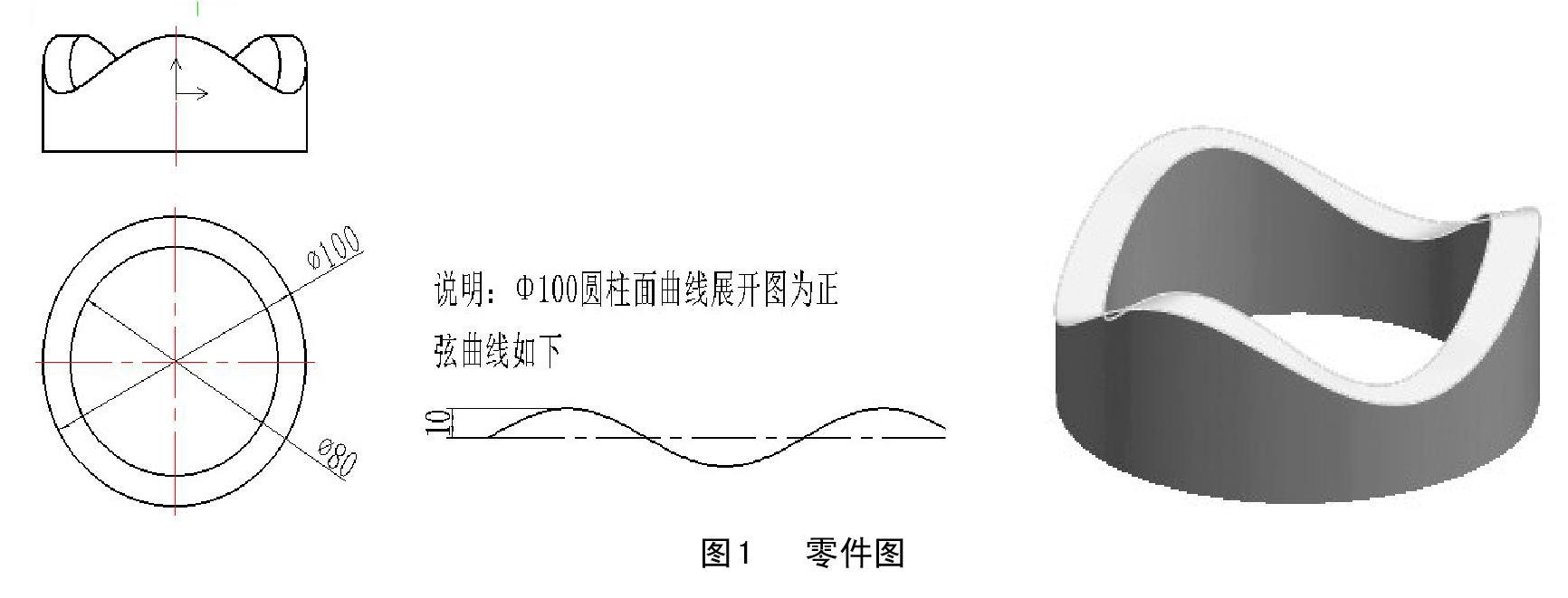
零件图如图1所示，要求未注线性尺寸公差应符合GB/T1804-2000，零件加工表面上，不应有划痕、擦伤等损伤零件表面的缺陷，去除毛刺飞边，曲线光滑过渡，曲面表面粗糙度为Ra1.6，其余Ra3.2，高50mm。件材料为45#钢，45#钢是机器中经常遇到的典型零件之一，主要用来支承传动零部件，传递扭矩和承受载荷。毛坯φ105×55mm，通过对零件图的进行分析，该零件最大的加工难度就是正弦曲线表面。在加工工艺上，先将外圆柱面、内孔粗精车至图纸尺寸要求，然后采用三爪自定心卡盘进行装夹，加持φ100圆柱面，以φ100的外圆表面作为定位基准，完成粗精铣削加工。在切削参数上，切削参数的合理选择直接影响着零件的加工质量、生产效率、刀具使用寿命。本例主轴转速为1200—2000r/min，背吃刀量0.025-0.06mm/刃，这样的切削参数保证其加工质量，提高了生产效率。在刀具选择上，本例选择了φ10球头刀进行粗精加工，球头刀主要是刀刃类似球头，用于铣削各种曲面、圆弧沟槽的加工，也叫R刀如图2，一般情况下，刀具半径的大小就是球头刀圆弧半径的大小。由于其几何结构，在铣削过程中接触面积大、主切削力大，因此在铣削过程中切削深度较小，生产效率低。为提高生产效率，通常情况下，采用少吃快走的加工策略，以便提高加工效率。虽然其加工效率较低，但加工余量均匀，尤其是对曲面加工效果更明显，表面质量更高。如果选择立铣刀，虽然加工效率较高，但由于零件轮廓形状的结构，在铣削过程中，会产生加工余量不均匀，存在着过切或欠切现象，影响表面加工质量。

编程方法与分析

通过对图1零件结构分析，零件曲面由正弦曲线构成，本例采用手工编程。就目前而言，数控系统还没有开发出一条指令用于曲线、曲面加工，针对系统中存在的缺陷，编程程人员都是借助数控系统已有的功能直线插补或圆弧插补，采用该功能拟合曲线的方法，编制其加工程序，这种编程就是数控宏程序编程，是用变量的方式进行数控编程的方法。首先将曲面转化为曲线，推导出曲线方程或参数方程，数控铣床一般采用参数方程，然后定义变量，通过变量的变化，引起曲线变换，完成曲面程序编制，编程过程如下：

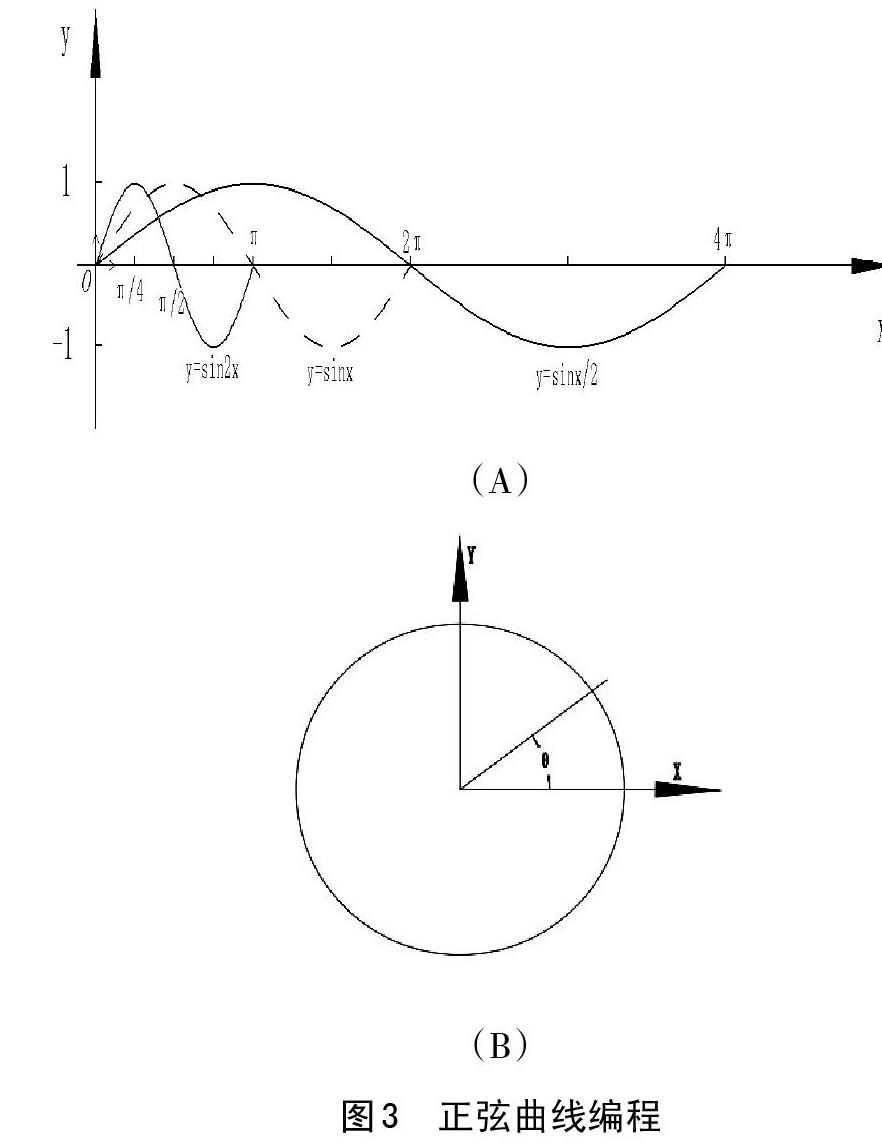
圆的参数方程：X=R*COSθ，Y=R*SINθ;R为圆的半径，θ为变量圆心角角度，XY为圆上的点坐标如图3B。正弦曲线：y=A*sin（ωx+θ）;A为波幅（纵轴），ω为角频率，x为时间变量 （横轴角度），θ为相偏移（横轴左右）如图3A。刀具在XOY平面中的两个圆之间做往复运动，Z轴做正弦曲线运动从而得出所要加工的曲面。设圆的圆心角θ为变量#1使得圆变成若干个点直线相连逼近圆的曲线。得出圆上点的坐标为：Φ100的圆上点坐标X=50*COS#1，Y=50*SIN#1，Φ80的圆上点坐标X=40*COS#1，Y=40*SIN#1

图3所示，可以利用函数的周期性，可以把y=sinx图形向左、向右缩放或拉升，得出y=sin2x，y=sin1/2x。可以看做是y=sin2x的图像是把y=sinx的图像上所有点的横坐标缩短到原来的1/2倍而得来的（纵坐标不变）。同理，y=sin1/2x的图像是把y=sinx的图像上所有点的横坐标伸长到原来的2倍而得来的（纵坐标不变）。得出结论函数y=sinωx的图像是吧y=sinx的图像上点的横坐标缩短或者伸长到原来的1/ω倍而得来的（纵坐标不变）。最终得出，正弦曲线上x为横轴（圆的角度）在整圆上（2π=360度）有3次重复，缩短了原来的1/3倍，得：y=sin3x= sin（3*#1），图一所示正弦曲线波幅A为10 得出图一的正弦曲线为y=10*sin（3*（#1）），正弦曲线第一个周期是从圆的零点开始的Z值应该是-10，所以Z轴的坐标值为10*sin（3*（#1））-10。使用Φ10的球头刀加工，模拟轨迹如图4，参考程序如下：

结束语

本文针对宏程序在数控铣削中应用进行了研究，具有参考价值，也能满足工件的精度要求，在实际加工中可以调整变量的增量，就可以使加工曲线逼近曲线的误差，提高加工精度。解决了圆环上正弦曲线的相关问题及编程加工思路，對数控铣床加工相似类型零件提供了参考。

参考资料：

[1]徐衡.FANUC数控系统手工编程[M].北京：化学工业出版社2017.06

[2]刘蔡保.数控编程[M]. 北京：化学工业出版社.2018.9

[3]杜军.FANUC宏程序编程技巧[M].北京：化学工业出版社.2016.6

[4]辜文娟.浅谈宏程序在数控铣床编程的应用[J].机械研究与用，2016，29（04）

[5]马国伟.数控铣加工工艺的应用与优化[J].科技经济导刊.2019，27（26）：82

[6]张辰.宏程序在数控编程中的应用研究[J].河南科技，2019（22）：86-88.