日光温室内浅层土壤温湿度场的数值模拟
2020-03-13杜震宇
张 艳,杜震宇
(太原理工大学 环境科学与工程学院,太原 030024)
近年来,日光温室在我国农业发展中取得了显著成就,已成为我国农业的主要生产形式,但日光温室内热湿环境比较复杂,室外气象条件、围护结构、土壤物性参数、作物的生长等都会影响室内温湿度的调控,从而影响室内作物的产量[1-3]。由于土壤的蓄放热对温室的热湿环境有着决定性的影响[4],因此有必要对土壤温湿度场进行研究,为研发低成本、运行费用低、节能的温湿度调控装置奠定基础,以提高日光温室的热湿环境调控技术。国内外学者对于日光温室热湿环境已做了部分研究。SHARMA、TIWARI et al[5-6]等利用Runge-Kutta方法分析温室室内空气热湿交换规律,建立了考虑导热、对流等作用的能量平衡方程,但未给出土壤区域的相关方程。FAYER[7]提出了土壤热湿传递的理论模型,但忽略了土壤温度梯度对水分传递的影响。杨艳超[8]对山东省日光温室微气候条件的模拟研究表明日光温室内潜热、显热的变化趋势与太阳总辐射相一致。刘宏[9]对日光温室土壤-空气换热器的换热特性进行了试验研究,测试了不同空气流速换热管内空气温湿度和换热管周围的土壤温度,得出了最佳入口空气流速。李钰楠[10]使用Visual Basic6.0编写了土壤热湿耦合迭代求解软件,探究了土壤物性等初始计算参数对土壤-空气换热器埋地换热管周围土壤温湿度场的影响。范毅等[11]对日光温室环境下土壤空气换热器的换热特性进行了研究,分析了试验工况下土壤空气换热器的动态换热过程及系统性能变化规律。YENER et al[12]对自然条件下土耳其不同区域不同深度土壤温度进行理论与试验研究,分析比较了土壤温度与空气温度的变化规律。MAHDAVI et al[13]分析比较了自然条件下有秸秆覆盖与裸土浅层土壤蒸发量的变化。
由此可见,国内外学者做了大量有关温室室内温湿度、热环境以及土壤-空气换热器埋管周围土壤温湿度场的研究,对于浅层土壤的研究多为裸露在室外的土壤,且忽略了湿度场对温度场的影响,对日光温室内浅层土壤温湿度场的理论与试验研究都很少。本文利用Fluent15.0对日光温室浅层土壤(注:≤100 cm深度)温湿度场进行三维非稳态数值模拟,在此基础上利用该模型研究了大尺度内浅层土壤温湿度场的变化规律,旨在为研发日光温室热湿环境调控装置提供科学依据。
1 试验内容
1.1 供试日光温室
该试验所用日光温室位于太原市小店区,坐北朝南,方位角为南偏西5 °,南北跨度9.7 m,东西净长50 m,后墙高度3.1 m.南面采光面为塑料薄膜,在膜的最底部和顶部有可启闭的通风口,可以将热湿空气排出[14]。温室结构尺寸如图1所示。
建立一个三维直角坐标系,见图1.以水平向西为Z轴正方向,以水平向南为X轴正方向,以垂直于地表指向天空为Y轴正方向,以温室地表面东西向与南北向中部位置的交点为坐标原点。
1.2 测点布置与编号
供试温室没有种植作物,地面为裸地。试验测点布置在温室中部的位置,如图2所示。为方便讨论,将试验所布置的三个测点从北到南依次命名为测点1、测点2、测点3.在图2所示测点位置距地表30 cm范围内的土壤层内埋设土壤温湿度传感器,测点的具体位置及编号如图3所示[15]。

图2 南北向测点位置及编号(单位:mm)Fig.2 North-south position and number of measuring points(unit:mm)
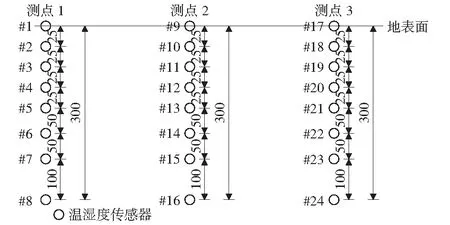
图3 土壤层(≤30 cm)测点位置及编号(单位:mm)Fig.3 Soil layer (≤30 cm) measuring points location and number(unit:mm)
1.3 数据采集与整理
试验数据的采集时间为2017年3月11日—3月25日。通过传感器采集土壤温湿度,自动储存至数据采集仪。存储的数据可通过USB端口导入计算机内,进行数据整理与分析。
2 理论模型
2.1 物理模型
本模型中没有考虑室内作物,所以认为地面为裸地。地面的热湿过程包括:土壤垂直方向的热量传递,与室内空气的热对流交换,与室内各个面的长波辐射热交换,吸收的太阳直射辐射、散射辐射,土壤表面水汽相变传递的热湿量等热湿交换过程。图4为日光温室地表能量收支示意图。

图4 日光温室地表能量收支示意图Fig.4 Sketch of the surface heat balance of sunlight greenhouse
温室内地表面能量平衡模型方程如下:
Q+I+H+L-γW=0 .
(1)
式中:Q为热传导热量,J;I为太阳辐射量,J;H为对流辐射换热量,J;L为长波辐射换热量,J;γ为汽化潜热,J/kg;W为水分传输量,kg.
本文对实际模型进行简化和假设,建立了浅层土壤温湿度场的三维非稳态数值模型。采用CFD数值计算方法,考虑了多变的太阳辐射和室外环境条件,用UDS定义土壤含水率,编写湿方程的UDF程序,导入Fluent中对日光温室浅层土壤温湿度场进行数值求解。
2.2 数学模型
模型简化假设:
1) 采用Boussinesq假设,以便于处理由于温差而引起的浮升力项;
2) 将温室围护结构材料视为常物性的固体材料,土壤视为多孔介质;
3) 不考虑土壤中水分的宏观流动,忽略重力对土壤内水分的影响;
4) 土壤中的水蒸气与温室内的湿空气遵循理想气体状态方程。
空气区域控制方程包括如下方程。
连续性方程:
(2)
动量方程:
(3)
(4)
(5)
(6)
能量方程:
(7)
k方程:
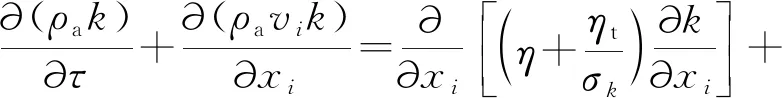
(8)
ε方程:
(9)
土壤区域的湿迁移方程:
(10)
(11)

参考文献[16]给出的DT、Dθ的拟合公式:
DT=-2.349 5×10-5·θ6+2.037×10-5·θ5- 6.694 6×10-6·θ4+1.043 8×10-6·θ3- 7.869 9×10-8·θ2+2.735+10-9·θ+ 5.403 9×10-12.
(12)
Dθ=2.217 6×10-6(θ6·e-7) exp(-2.09×10-3·T) .
(13)
其中,e为土壤孔隙率,本文取砂土孔隙率0.37.
2.3 几何模型
利用ICEM CFD 15.0软件建立日光温室和土壤的几何模型,土壤厚度100 cm.鉴于温室结构的不规整性,结构化网格划分比较困难,计算结果不准确,而非结构网格能对不规整模型进行划分,生成高质量的网格,所以选择使用ICEM CFD非结构网格划分。计算区域网格划分如图5所示。

图5 模型网格划分Fig.5 Model mesh generation
2.4 网格独立性考核
数值模拟结果的准确性与网格数目有很大关系,网格数目过多会导致计算机计算时间过长,数目太少会影响计算结果的准确性,因此采用数值模拟计算进行网格独立性考核,本次模拟共选取了5套网格,网格数量分别为:515 720、1 032 885、1 456 720、1 852 662和2 216 874.如表1所示,选取同一时刻测点1的温度值进行独立性考核,网格数1 852 662测点1温度值为17.9 ℃,网格数2 216 874测点1温度值为17.8 ℃,相对误差小于1%,考虑到计算时长以及模拟结果的准确性,本文选取网格数量1 852 662来进行数值模拟。
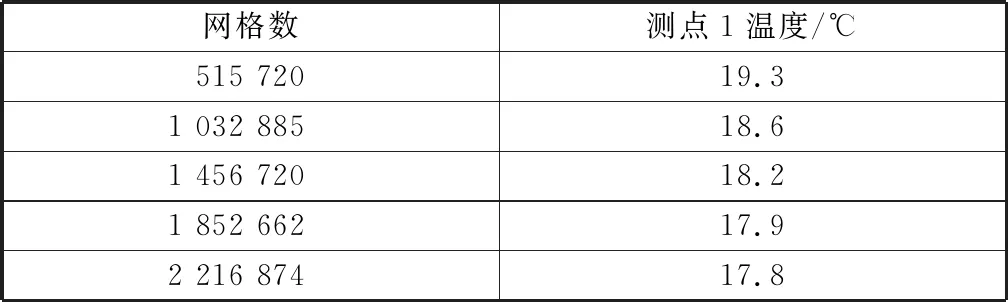
表1 网格独立性考核Table 1 Mesh independence test
2.5 数值计算方法
控制方程的求解采用有限容积法,采用SIMPLE算法处理压力与速度的耦合关系,对流项的离散格式采用三阶精度的QUICK格式。数值模拟采用RNGk-ε湍流模型,非平衡壁面函数,DO辐射模型。用UDS定义土壤含水率,编写湿方程的UDF程序,导入Fluent中进行数值求解。模拟计算从3月11日18时00分起,时间步长300 s,连续计算2 d.
2.6 边界条件
模型的计算域为日光温室内的空气区域与深度为100 cm的土壤区域,地表面既与温室内空气进行传热传质,也与土壤层存在温度与水分的传递,因此将地表面设为流固耦合面,温室围护结构和塑料薄膜设为第三类边界条件,材料的物性参数如表2所示,将来风面设为velocity-inlet边界条件,风速为2.5 m/s,将实测的室外空气温度回归拟合出空气温度随时间变化的函数,将公式编入UDF,设为入口温度边界条件,出口设为outflow.将土壤的原始温度场编入UDF,设为土壤原始温度,作为土壤的边界条件。将土壤深100 cm处的含湿量测量值设为土壤的初始体积含水率,即0.2 m3/m3.
围护结构与室外空气的对流换热系数与室外风速有关,具体计算式为[17]:
h=18.63v0.603.
(14)
式中:v为围护结构外表面的实际风速,其值大小与大气风速v有关。
对于背风面:v=0.3+0.05v.
对于迎风面:
当v≥2 m/s时,v=0.25v.
当v<2 m/s时,v=0.5.
太原地区的主导风向为西北风,平均风速2.5 m/s,围护结构的对流换热系数以及边界条件的设置见表3.
土壤的原始温度场
(15)
土壤的原始温度场由崔良卫等[18]计算得出,Ω为温度波波动频率,7.17×10-4rad/h;a为导温系数,m2/h;td为地表年平均温度,试验地取11.3 ℃;Ad为地表温度波振幅,试验地取17.75 ℃;y为地层深度,m;t0为土壤原始温度,℃.

表2 材料的物性参数Table 2 Material properties
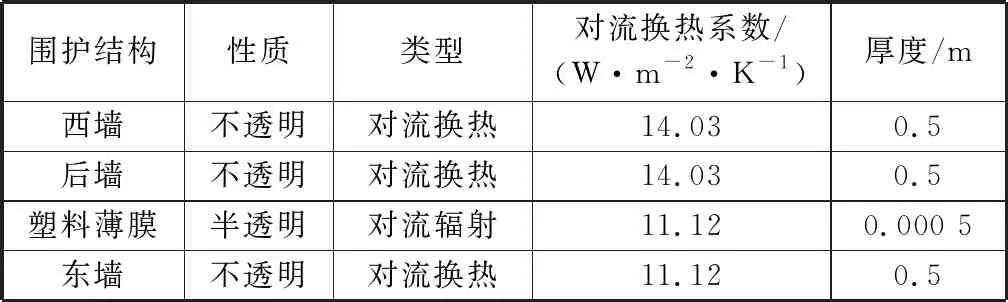
表3 边界条件Table 3 Boundary conditions
3 结果与讨论
3.1 模拟验证
测点1、测点2、测点3土壤温度的模拟值与试验值的对比结果如图6所示,测点1、测点2、测点3土壤含水率的模拟值与试验值的对比结果如图7所示,测点1(Y=0)、测点2(Y=0)、测点3(Y=0)模拟值与试验值吻合较好,温度平均相对误差小于3.8%,含水率平均相对误差小于2.6%,在工程测量的误差允许范围内。故模型具有一定的合理性,数值模拟方法具有可靠性。
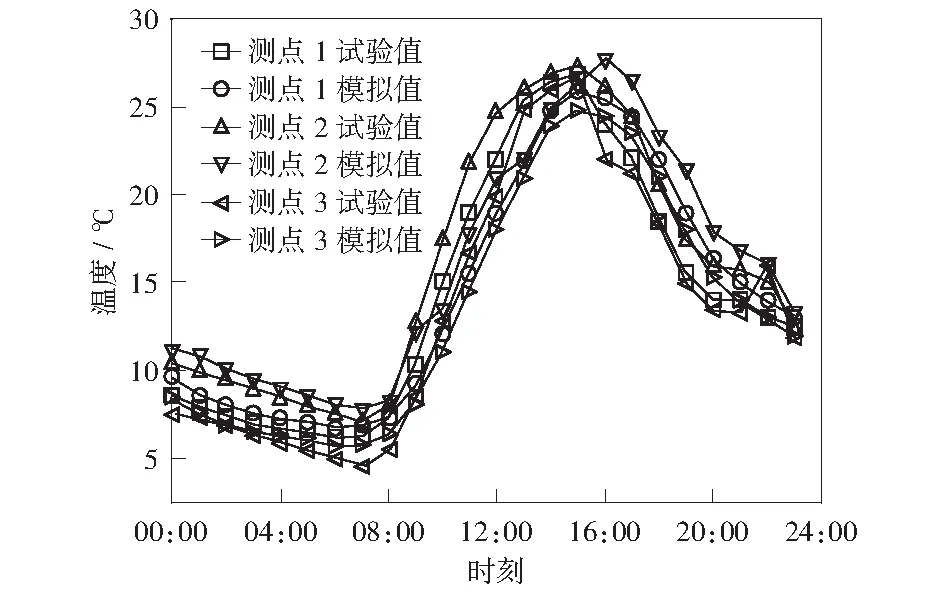
图6 温度场验证Fig.6 Temperature field verification

图7 湿度场验证Fig.7 Moisture field verification
3.2 土壤温度场与湿度场的分布
图8为数值模拟出不同深度土壤层温度随时间的动态变化图,从图中可以看出,不同深度的浅层土壤(注:≤100 cm深度)温度变化趋势一致,都随时间呈现周期性的变化。随着土壤深度的增加,温度波的振幅逐渐减小,延迟时间逐渐增大。当地表温度高于土壤层温度时,热量从地表向地下传递,土壤层温度高于地表温度时,热量从地下向地表传递。不同深度的土壤地温变化幅度均表现出5 cm>10 cm>15 cm>20 cm>30 cm>40 cm>50 cm>100 cm的变化规律,即越靠近地表土壤层温度日较差越大,0~30 cm土壤层温度在一天内的波动振幅为19.7~7.2 ℃,土壤层温度受气象条件和环境变化影响较大,土壤温度波动显著;30~50 cm土壤层温度在一天内的波动振幅为3.6~0.4 ℃,土壤层温度受气象条件和环境变化影响较小,土壤温度波动不太明显;50~100 cm土壤层温度在一天内的波动振幅小于0.5 ℃,土壤层温度处于比较稳定的状态,基本不受气象条件和环境变化的影响。根据不同深度浅层土壤温度梯度的变化规律,可以把0~100 cm的土层分为三个特征层:多变层(0~30 cm),缓变层(30~50 cm),均稳层(50~100 cm).随着土壤深度增加,最高气温与最低气温出现的时间总体上也相对滞后。
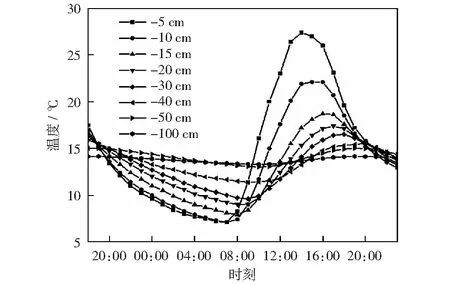
图8 土壤温度场(≤100 cm)Fig.8 Soil temperature field (≤100 cm)
浅层土壤中不仅存在水蒸汽的冷凝蒸发,还存在多孔介质传热传质的Soret效应和Dufour效应[19],重力、达西阻力、土壤温度以及湿分梯度引起的毛细力的共同作用,图9为数值模拟出不同深度土壤层的含水率随时间的动态变化图,分析图可知,不同深度的土壤湿度变化趋势一致,都随时间呈现周期性的变化。随着土壤深度的增加,含水率的变化幅度逐渐减小,延迟时间逐渐增大。到50 cm深度的土壤层含水率基本不随环境温湿度的变化而变

图9 土壤湿度场(≤100 cm)Fig.9 Soil moisture field (≤100 cm)
化,趋于恒定。当温室内的空气温度高于地表面土壤温度时,地表土壤中的水分吸收空气热量蒸发,地表面温度低于空气的露点温度时,水蒸汽遇冷凝结成水滴,水蒸汽冷凝放热,地表面吸热。
3.3 土壤不同初始体积含水率下温度场的变化
图10为数值模拟出的土壤不同初始含水率条件下浅层土壤(注:≤100 cm深度)温度场的变化。取0:00测点1的结果图,可以看出,在其他初始条件相同的情况下,不同土壤初始体积含水率下土壤温度随深度的变化规律一致。土壤初始体积含水率越低,浅层土壤层的温度梯度越大。当土壤初始体积含水率为0 m3/m3时,土壤层温度梯度最大;当土壤初始体积含水率为0.3 m3/m3时,土壤层温度梯度最小。这是因为:在土壤初始体积含水率较高的情况下,土壤热容量较大,温度传播得较慢,而在土壤初始体积含水率较低的情况下,土壤热容量较小,温度传播得较快。
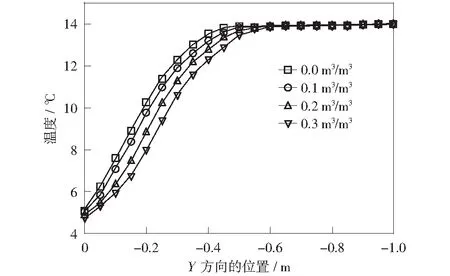
图10 不同土壤初始体积含水率下土壤温度变化Fig.10 Variations of soil temperature under different soil volume moisture
图11为取12:00测点1的结果图,可以看出,在其他初始条件相同的情况下,土壤初始体积含水率越低,沿Y方向的土壤层温降梯度越大。当土壤体积含水率为0 m3/m3时,沿Y方向的土壤层温降梯度最大;当土壤初始体积含水率为0.3 m3/m3时,沿Y方向的土壤层温降梯度最小。同样验证了:土壤初始体积含水率越低,土壤热容量越小,温度传播得越快,而在土壤初始体积含水率较高的情况下,土壤热容量较大,温度传播得较慢。

图11 不同土壤初始体积含水率下土壤温度变化Fig.11 Variations of soil temperature under different soil volume moisture
4 结论
本文建立了浅层土壤温湿度场的三维非稳态数值模型,对日光温室浅层土壤(注:≤100 cm深度)温湿度场以及土壤不同初始体积含水率下温度场的变化进行了模拟,得出以下结论:
1) 日光温室内浅层土壤不同深度的温湿度变化趋势一致,都随时间呈现周期性的变化,随着土壤深度的增加,温度波的振幅逐渐减小,含水率的变化幅度也逐渐减小,延迟时间逐渐增大, 最高气温与最低气温出现的时间总体上也相对滞后,50 cm深度土壤层温湿度基本保持恒定。
2) 土壤初始体积含水率越低,沿Y方向的土壤层温降梯度越大,温度传播得越快;土壤初始体积含水率越高,沿Y方向的土壤层温降梯度越小,温度传播得越慢。
3) 根据不同深度浅层土壤温度梯度的变化规律,可以把0~100 cm的土层分为三个特征层:多变层(0~30 cm),缓变层(30~50 cm),均稳层(50~100 cm).
