±800 kV直流输电线路带电作业电位转移电场特性分析

2020-03-12李智琦周晨梦罗日成

电力学报 2020年1期

李智琦，刘众，张巍，周晨梦，吴静，罗日成

(1.国网湖南省电力有限公司常德供电分公司，湖南常德 415000；2.长沙理工大学电气与信息工程学院，长沙 410114；3.国网湖南省电力有限公司长沙供电分公司，长沙 410007；4.国网湖北省电力有限公司直流运检公司，湖北宜昌 443001，5.国网湖南省电力公司检修公司，长沙 410015)

0 引言

为保障超/特高压输电线路持续运行的稳定性和经济性，常需对输电线路进行带电维修和检查[1]。当作业人员进入等电位点进行带电作业时，作业人员需穿戴屏蔽服，并按照一定路径进入电场，再通过手持电位转移棒接触运行线路，从而使作业人员的人体电位与运行线路形成等电位，该过程即为电位转移过程。±800 kV特高压直流输电线路带电体周围电场强度(以下简称场强)高，进行电位转移时，作业人员与导线间将产生放电现象[1]。电位转移过程主要分为转移前以及转移后两个阶段，即在±800 kV线路带电作业时，当作业人员进入电场与导线间的距离达到一定范围时，因局部场强过大导致导电手套或电位转移棒尖端形成放电电流，该过程为转移前阶段的流注放电；穿戴屏蔽服的作业人员通过导电手套或者电位转移棒等专业工具接触极导线时，因作业人员与导线之间分布电容储存的电荷会发生放电而产生的电流，称为转移后阶段的电位转移电流。如果带电作业的安全防护措施考虑不周，电位转移过程产生的放电电流和暂态能量极有可能威胁到作业人员的人身安全和输电线路的运行安全[2]。

近年来，已有较多针对±800 kV输电线路带电作业的研究。文献[3]运用有限元仿真软件建立了±800 kV带电作业的等比例模型，分析了电位转移过程中典型位置的人体体表场强值，并提出了应采取的屏蔽措施。文献[1][4][5]研究了±800 kV输电线路带电作业技术参数、人员安全防护、工器具的研制及标准的制定，对电位转移过程中的电位转移电流进行了测量，同时运用电磁计算软件建立并计算了转移电流值。文献[6][7]建立了±800 kV带电作业三维有限元模型，在计算了典型工作位置人体体表场强的同时，利用电磁分析软件对转移过程中的电流进行了分析。上述研究成果研究了带电作业过程典型位置处的人体体表场强，分析了电位转移过程后阶段的转移电流而并未提及前期流注放电过程。对于特高压直流电位转移没有明确的作业规范，不能全面评估电位转移的风险，更难以确保进出等电位作业人员的安全。

为更加全面地评估电位转移的安全性，需要系统地对电位转移过程中人体与导线、人体与大地之间的电场特性加以研究。本文综合分析了±800 kV带电作业电位转移过程，针对电位转移过程前后两个阶段建立了等效模型，即模型分为两个部分：一个为电位转移前阶段流注放电过程，考虑到局部放电的过程，搭建流注放电模型，计算该放电过程中的流注发展场强变化、电流密度，并总结其变化规律；另一个为将转移后阶段等效为三导体系统，搭建出暂态响应计算模型，计算该过程的电位分布和转移电流变化情况。最终分析不同转移距离下人体电位、放电电流以及放电能量确定了安全防护重点，以降低作业风险，为保障作业人员的生命安全及输电线路带电作业的顺利开展提供了一定的理论参考。

1 前阶段流注放电过程分析

为分析带电作业的电位转移前的放电特性，首先建立流注放电模型，计算并分析电位转移距离为0.3 m的放电特性。由于目前还未有特高压直流输电线路电位转移放电特性相关试验研究，因此本文将研究结果与已有的大气压下流注放电的理论和结果进行对比分析。

1.1 流体力学模型

带电作业电位转移的放电几何模型是由人员手持的电位转移棒和分裂导线构成。在分析放电过程中，综合考虑计算的有效性，通常将分裂导线用等效半径导线代替，可近似为板模型，电位转移棒近似为棒模型，其放电过程可用棒-板结构的放电过程解释。本文采用的放电模型几何结构如图1所示，图1(a)是棒-板间隙放电的整体模型效果图，其中A为棒极，B为板极。由于仿真模型具有二维轴对称性，为减少网格划分并提高运算速度，计算区域选取图1(a)中的虚线框abcd区域，如图1(b)所示，B4为对称轴。其中，棒电极的长度为0.4 m，直径4 mm，棒头为半圆，曲率半径为1 mm。空气间隙的长度可以根据要求在0.3～0.6 m之间进行变动。

电位转移放电过程的流体力学模型由电子、正负离子的连续性方程(1)—(3)和电场的泊松方程(4)构成[8-9]：

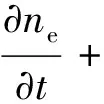
(1)

(2)

(3)

ε2φ=-q(np-ne-nn),E=-φ.

(4)

式中：下标e，p，n分别表示电子、正离子和负离子；ne，np，nn分别为每立方米电子、正离子和负离子的数量；μ表示迁移率，m2/Vs；D表示扩散系数，m2/s；E表示电场强度，V/m；t表时间；ε表示空气介电常数；φ表示电位，V；q表示单位电荷量，C；源项主要考虑电子碰撞电离速率Rion=αneueE；电子与空气中带电负性分子之间附着速率Ratt=ηneueE；电子从负离子分离速率Rdet=kdetnenn；电子与正离子复合速率Rep=βepnenp；正负离子复合速率Rpn=βpnnpnn。在以上表达式中输运参数α为电子碰撞电离系数，m-1；η电子的附着系数，m-1；βep电子与正离子的复合系数，m3/s；βpn正负离子复合系数，m3/s。

1.2 场强变化

在一定条件下流注发展的快慢会对间隙中整体电弧放电发展过程产生影响。在0.3 m转移距离下进行电位转移时，前期的流注放电阶段沿着轴线的电场分布如图2所示。图2中轴向距离0 m处为板极，0.3 m处为棒极。随着流注放电的继续发展，流注头部的电场强度减小，当放电时间为40 ns时，流注头部最大电场强度稍微上升，即流注头部几乎到达板极，此时可近似认为流注贯穿整个放电间隙并且流注头部最大电场强度为1.67×106V/m。

1.3 电流密度特性

不同时刻下棒极表面的电流密度如图3所示，横坐标0 m为棒极轴线处。由图3可知电流密度随着时间的增加而增大，轴线处的电流密度最大并沿着电极表面向外逐渐减小，这是因为轴线处的场强最大并沿着电极表面向外逐渐减小。模型计算的电流密度趋势与文献[10]大气压下空气放电研究结果基本一致。根据棒极电流密度计算可得到0.3 m的作业间隙平均放电电流为17.9 mA。

2 后阶段暂态响应过程分析

电位转移过程中存在两种放电电流：其一是电位转移前的局部放电电流，其值一般较小，即流注放电电流，该流注放电过程已在上一章节做了具体分析；其二是作业人员由中间电位转移至等电位的暂态过程中，电容储存的电荷放电产生了脉冲电流，即转移电流。为了分析电位转移后阶段电容暂态放电过程，本节采用ATP-EMTP电磁暂态分析软件建立了暂态响应等效数学模型，计算并分析了转移距离为0.3 m时作业人员的人体电位和脉冲电流的变化规律。

2.1 暂态响应计算模型

带电作业人员按照指定路径进入电位转移的作业位置点，此时作业人员位于导线和杆塔之间，即为悬浮电位状态，其平面位置示意图如图4所示。此时作业人员、导线以及铁塔构成了一个三导体系统，已有研究表明此三导体系统间的空气隙间可等效为空间电容，其电容值与间隙的距离有关[11-12]。

作业人员进行电位转移瞬间的等效电路图如图5所示，图5中C1表示人与导线间等效电容；C2表示人体对杆塔、大地之间的等效电容；C3表示导线对大地的等效电容；R1表示人体和导线间的绝缘电阻；R2表示人体和杆塔之间的绝缘电阻，R3表示导线和大地之间的电阻，且R2≫R1，R1+R2≈R3(忽略人体短接部分的绝缘电阻)。根据文献[5]，给出R1和R2的数值分别取500 kΩ和2 GΩ。

在电位转移后期暂态响应过程中，作业人员的悬浮电位V1取决于电容大小，而在等电位后稳态时作业人员的电位取决于绝缘电阻大小，其表达式如式(5)(6)所示，式中U3为线路的工作电压[13]，即本文为±800 kV。

(5)

(6)

作业人员由转移棒进入等电位点瞬间等效为图5中开关S闭合时的情况，该过程是由人体与极导线间等效电容所储能的电荷放电产生了转移电流，因此在计算电位转移中人体电位以及转移电流大小的关键是计算等效电容值。本文采用三导体系统的等效集总电容求解，图6中导线的自电容为C11；人体的自电容为C22；导线和人体之间的互电容分别为C12，C21；U1和U2分别表示导线、人体的电压降。假设系统集总电容矩阵表示为CJ=[C11C12C21C22]，即感应电荷Q1和Q2可用集总电容与电压降表示为：

Q1=(C11+C12)U1-C12U2,

(7)

Q2=(C12+C22)U2-C12U1.

(8)

以复丰线路直线塔为例，对作业人员与导线间的距离(即转移距离为0.3～0.6 m的情况下)进行电位转移暂态响应过程研究，忽略导线和大地间电容C3产生的影响。极导线对地电位为800 kV，采用Ansoft软件可计算出的作业人员采用吊篮法作业方式进入电场后转移距离为0.3～0.6 m时的人体周围的电位分布。通过人体电位大小可求得各个转移距离下的导体间电容见表1，由表1中数据可知，随着转移距离的增大，C1递减而C2增加，符合电容的基本定义。本研究所使用的转移棒是由铜质材料制成，其自阻可忽略不计，根据文献[2][5]的研究结果，本文取电感为0.01 mH和接触电阻为100 Ω。

表1 不同转移距离时间隙电容

2.2 人体电位

作业人员在到达指点转移位置过程中人体是处于悬浮电位的，当准备进行电位转移时周围会产生电晕放电、弧光放电等现象，这些局部放电不仅会给等效电路图5中的电容C1放电和C2充电提供一个通道，还会改变极导线与人之间的电压特性。作业人员在转移距离为0.3 m处采用转移棒进行电位转移时，根据模型可计算得到人体电位变化情况如图7所示，可见在电位转移过程中人体电位呈现振荡式变化，大约经过1 μs的振荡时间后与极导线电位保持一致，实现等电位。

2.3 转移电流

作业人员在与极导线间转移距离为0.3 m处进行电位转移后的转移电流计算结果如图8所示，电流波形呈脉冲式变化，随着时间变化振荡衰减为零，该过程衰减时间极短，大约为1 μs，电流最大为301.07 A。其电流形态变化与文献[5]中试验实测的结果相符。

3 转移距离的影响

本节对0.3～0.6 m范围内进行电位转移时人体电位和放电电流的变化情况进行分析。

3.1 人体电位分析

不同转移距离下作业人员采用转移棒进行电位转移后人体电位的变化情况如图9所示，作业人员与极导线之间的电位差如图10所示。由图9与图10可见，在该电位转移过程中各转移距离下人体电位均呈现振荡式变化，都大约经过1 μs的振荡时间后作业人员的人体电位逐渐达到极导线的电位值，最终实现等电位；但作业人员与导线之间的电位差随着转移距离减小而增大，转移距离为0.6 m时电位差最大，该值大约为160 kV。由此可见不同转移距离对人体电位幅值有明显的影响而对实现等电位速率的影响并不明显。

3.2 放电电流分析

在电位转移前阶段流注放电过程中，不同转移距离下流注放电贯穿时带电作业人员与导线之间形成等离子通道，此时放电电流密度如表2所示。可见随着转移距离增大，电流密度逐渐减小，这是因为在空气放电过程中作业人员与导线之间产生放电电流主要是由电子和正离子的定向移动形成的，当放电距离增大后，发生碰撞电离次数增多，电子头部的半径增大，电子的移动速度减小，因此放电电流会随着转移距离的增大而减小。又因为在面积不变情况下放电电流与放电电流密度成正比，所以随着转移距离增大，电流密度逐渐减小。

表2 不同距离下电流密度大小

根据转移前流注放电过程电流密度大小可以计算出当转移距离分别为0.3 m，0.4 m，0.5 m，0.6 m时对应的放电电流大小为17.9 mA，14.7 mA，9.04 mA，5.08 mA，即随着转移距离的增加，放电电流减小。目前还未有对该带电作业放电电流的试验测量，因此参考关于直流输电线路电晕电流放电相关文献的电流测量结果均为毫安级别，即本文放电电流结果与其量级相符合[14]。

在电位转移后阶段暂态响应过程中，不同转移距离下转移电流变化情况如图11所示。即当转移距离分别为0.3 m，0.4 m，0.5 m及0.6 m时，与之对应的电位转移电流幅值分别为301.07 A，313.02 A，326.08 A和334.95 A。由图11显而易见的是转移电流大小随着转移距离的增加而增大。参照电工学基本原理，进行电位转移时，作业人员与导线距离越远，该“拉弧”过程所产生的脉冲电流就会越大。可见以上所得结果符合电工学基本原理[2]。

通过放电电流和电位转移电流变化规律可知电位转移距离越大时转移电流就越大，对作业人员的人身安全是不利的；转移距离越小时放电电流会更大，极容易造成弧光放电，这对作业也是不利的。因此电位转移过程中存在一个最佳的转移距离。

3.3 转移能量分析

电位转移过程中的间隙放电伴随着能量的释放，释放的能量大小是作业人员人身安全的一个重要评价因素，过高的能量可能烧蚀作业人员佩戴的导电手套或屏蔽服[2]。适用于带电作业电位转移过程中放电系统产生的能量计算公式可用式(10)得出：

(9)

(10)

式中，J(t)为棒极表面电流密度；S为棒极表面有效面积；i(t)为流入棒极的电流，与棒极表面的电流密度有关；r为轴对称模型中柱坐标r分量；u为棒极和板极间的电势差。

电位转移点距离输电导线的位置不同，产生的脉冲电流和暂态能量的大小也不同。电位转移距离的选取一般视综合情况而定，通常取0.4～0.5 m[5]。本文计算了0.3～0.6 m不同转移距离下的能量大小，计算结果如表3所示。

表3 不同转移距离下的能量

当电位转移时作用于导电手套的暂态能量达到1.0 J，导电手套可能会被烧蚀，转移电流由此流入人体，会危害作业人员的生命安全[2]。由表2可知，本模型计算得到的不同转移距离下释放的能量均约为1.0 J，随着转移距离的增大，释放的能量有所增加。当转移距离大于0.5 m时，转移能量已高于1.0 J。由于转移距离的增加，间隙间的电势差增大，因此计算得到的能量越高。而流注放电贯穿间隙时，转移至等电位过程仍未完全完成，转移能量势必增加，可能会大于表2中的能量值。

在电位转移过程中，手持电位转移棒进行电位转移时，放电发展形成的弧根在转移棒上，避免了导电手套被烧蚀。因此，为防止导电手套被烧蚀，在±800 kV输电线路上进行带电作业时，作业人员宜持电位转移棒进行电位转移。