基于BP-S混合模型的大坝安全监测技术研究

杨泽煌

（江西省德安县水利局，江西 德安 330400）

0 引言

大坝安全监控模型最常用的主要有统计模型、确定性模型和混合模型等[1]，这些模型均建立在数理统计的基础上，操作简便，能较好描述环境量与效应量之间的关系，被广泛应用于数据挖掘分析方法中。但这些模型均存在一些局限：第一，均基于所有观测数据之间都是相互独立的假设前提上，且建模时选取影响因子较难，否则可能会影响计算精度；第二，监测数据主要受环境影响，如气温、大坝徐变、降雨等，这些环境变量存在较强的非线性特征，线性回归适合分析确定线性因子的关系，遇复杂的非线性问题时具有一定局限性，导致模拟精度和预测效果均达不到要求。因此，寻找更为高效、准确的监控分析方法是当前亟待解决的问题。

我国在大坝安全监控分析方法上发展迅速，尤其在处理非线性问题上，出现了许多新的应用理论[2]，如时间序列、灰色理论、模糊数学、混饨理论、小波分析、人工神经网络等[3]，监控理论日趋完善。其中，人工神经网络是20世纪80年代以来兴起的新研究热点，由于其具有自组织、自适应性、联想能力等特点，在处理自然科学中非线性复杂问题中具有独特的优势，在大坝监控中具有较广的应用前景，如缪新颖[4]等人利用LM-BP神经网络进行大坝变形预测分析；仲云飞[5]等利用遗传算法进行大坝扬压力预测；何勇军[6]等给出了神经网络模型的输入输出因子和模型结构；谭志军[7]则利用神经网络对各测压管水位分布进行模拟，分析了坝体浸润线的分布规律。这些研究表明，神经网络通过不断优化算法、提高训练速度及预测精度，在大坝监测分析应用方面具有极大的挖掘潜力。为此，本文基于大坝安全监控统计模型，结合BP神经网络处理非线性问题的优势，建立统计模型与BP神经网络混合模型，并结合实例进行分析。

1 模型的建立

1.1 统计模型

统计模型主要是分析因变量与自变量之间的线性关系及影响程度，确定影响因子是判断统计模型优劣的关键所在。一般情况下，大坝渗流主要受上下游水位差、降雨量及坝体介质特征等环境因素影响，温度主要对混凝土坝影响较大，而对土石坝的渗流影响很小，可以不予考虑。因此，土石坝渗流影响因素归纳为水位分量H，降雨分量R及时效分量θ；水位分量包括当日库水位、前期库水位，降雨分量包括当日降雨量及前期降雨量，时效分量主要为土体结构的固结影响，用数学式子表示为[2]：

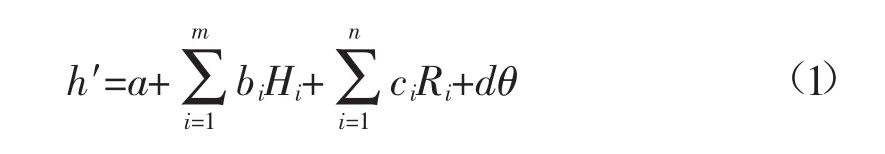
式中：h′为拟合测压管水位；a，bi，ci，d 为回归系数；Hi为i天前的水位；Ri为i天前的降雨量；θ为时效。

1.2 BP神经网络

基于BP神经网络的大坝渗流监控模型，实质就是将大坝渗流影响因素作为输入参数，所求值作为输出参数，对网络结构进行仿真训练，使系统输出结果逼近实际的监测值，具体步骤如下：

（1）输入层为所有影响大坝渗流压力的因子，包括上游水位、降雨量、时效等；

（2）输出层为大坝实测的管水位h，因此输出层节点数为1个；

（3）隐含层层数是影响网络训练结果的关键因素之一，直接影响网络性能优劣。Lippmann[8]指出2个隐层就可以解决任何形式的分类问题。Roberto Hecht Nielsen[9]证明了一个3层的网络可以完成任意n维到m维的映射，后来Roberto等人进一步指出，对于一个隐层的神经网络，只要隐节点足够多也可以逼近一个非线性函数。因此，本文选择单隐含层结构。

（4）隐含层节点数对于网络训练精度至关重要，一般采用经验公式估算或是试算方法来确定。金丕彦[10]等指出隐含节点应在网络容量和训练时间之间折衷；严太山[11]发现最佳隐含层节点数目与输入输出单元的多少以及训练样本数都有直接的关系，并归纳出估算最佳隐含层节点数目的简单实用的方法，具体如下：

式中：NH为最佳隐含层节点数；Ni为输入层节点数；N0为输出层节点数。

（5）激活函数和转移函数一般用logsig、tansig、purelin等3种函数，不同的函数对输出精度影响不同，如表1[12]所示，一般隐含层转移函数选用择logsig函数或tansig函数，输出层节点转移函数选择tansig或purelin函数。

1.3 BP-S混合模型的建立

上述的两种模型中，统计模型实质上是经验模型，它的优点是建模方法简单、直观，但是统计模型需要较长系列的监测数据。BP神经网络模型具有极强的非线性映射能力，在处理大坝非线性强的变量时具有优势，但预测精度不确定性较大。

表1 不同转移数对应预测误差

那么，可以建立起一种模型，使其既能具有统计模型的经验性，又能兼备BP神经网络模型的非线性映射能力，能进一步提髙模型的拟合精度和泛化能力。为此，本文在BP神经网络模型的基础上，结合统计模型，提出两者相结合的混合模型（以下简称BP-S模型），具体结构如下[13]：

（1）输入层为统计模型中的影响因子和统计模型的拟合值h′，各符号含义同统计模型，因此，输入层节点数在原有的节点数上增加一个，即为n+1；

（2）网络的隐含层数量及隐含层节点数量仍延用原模型；

（3）输出层为大坝的实测管水位值h与统计模型的拟合值h′之间的差值△h，因此，输出层节点数仍为1；

（4）求出差值之后，根据补差原理，利用h″=h′+△h，计算修正后的值，其中：h″为混合模型拟合的管水位。

到此，大坝安全监控BP-S混合模型就建立完成了[14]。

2 计算实例

某水库是一座以防洪为主，兼有供水、发电和灌溉等综合效益的大（2）型水库。其中大坝为粘土心墙坝。选取典型断面进行分析，该断面埋设了3个测压管，分别布置在坝顶及下游坡，坝体测压管典型断面图详见图1。

2.1 模型数据的选取

选取该坝2016年1月～2017年12月2年的监测数据。对数据进行预处理，剔除异常数据后，选择636个观测数据作为分析数据，其过程线见图2。其中，在神经网络建模中，选取2016年1月～2017年9月共580个数据作为训练样本，2017年10月～2017年12月共56个数据作为检验样本。

2.2 模型参数的确定

2.2.1 统计模型

（1）水位分量。从图2可知，UP401的滞后效应最不明显，而越往下游，滞后时间有所延长，但在5日之内，因此，在确定水位分量时，以当日H0、前1日H1、前3日H3、前5日H5共4个因子作为计算因子。

（2）降雨分量。降雨分量主要表现为降雨入渗作用，影响管水位变化。从图2可知，各测压管水位未见明显异常，变幅均在上游水位变幅以内，因此，降雨分量选择当日R0及前3日R3共2个因子作为计算因子。

（3）时效分量。时效分量主要表现为土体介质缓慢变化而导致渗透性变化，这种变化包括渗透性变小、变大或不变等。时效分量从2016年1月1日起，以0.01作为初始值，每日按0.01逐日增加。

2.2.2 BP-S神经网络

（1）输入层节点包括8个，分别有4个上游水位、2个降雨分量、1个时效分量以及1个统计模型拟合值h′，输出层为△h。

（2）将输入层个数及输出层个数代入公式（2），确定隐含层节点数为5个。

（3）学习速率β为1.2，平滑因子α取0.7，学习控制误差ε=0.01。

2.3 模型精度的比较

基于matlab神经网络工具，将上述数据分别代入统计模型、BP模型以及BP-S模型，计算结果如表2。

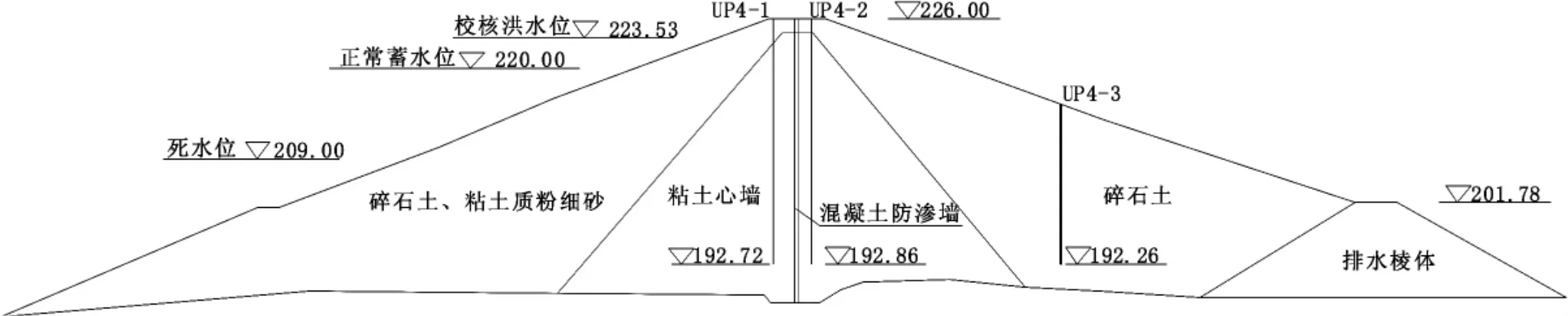
图1 坝体测压管典型断面图

图2 管水位变化过程线

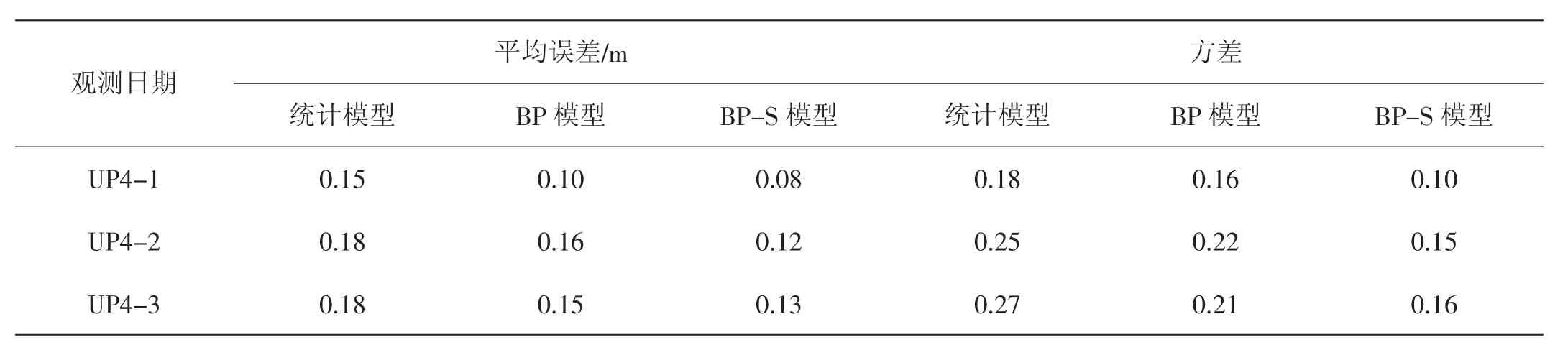
表2 不同模型的平均误差汇总表

通过表2可知，统计模型的精度最差，平均误差值达到了0.15以上，且靠近下游，UP4-2与UP4-3平均误差达到了0.18，方差在0.2以上；BP神经网络的精度有所提高，平均误差及方差降低10%～20%，而BP-S模型的精度最好，各测压管平均误差降低0.07、0.06、0.05，精度提高了约35%；从方差方面可知，BP-S模型方差分别降低44%、40%及41%，平均降低约42%，说明统计模型对数据的依赖度较高，误差分布较大，且易出现奇异值，而BP-S的模型精度较为稳定，对学习样本的数量要求偏低。

2.4 泛化能力分析

为了检验BP-S模型的泛化能力，选取2018年前3个月的实测数据进行预测。由于预测过程是基于实测值未知的前提下，因此，实测管水位h值采用已建立的BP网络模型模拟值代替，预测结果见表3和图3所示。

从计算结果可知，采用BP-S模型的各测压管水位预测精度较好，各测压管水位残差平均值分别为0.037m、0.049m、0.053m，平均值在0.04m 左右，这说明通过BP-S模型具有较强的预报能力。但从图3可知，UP401预测能力最好，而UP402及UP403的中后期的预测偏差略大，长期预报能力有所降低。

4 结论

大坝安全监测资料是实现大坝监控最有效的手段之一，传统的统计模型处理实际工程的非线性关系上存在一定的局限性，因此，本文将BP神经网络引入到统计模型中，利用神经网络处理非线性关系的优势，建立了BP-S混合模型，通过对比统计模型、BP神经网络及BP-S三种模型的计算结果，BP-S模型模拟精度明显提高，预测效果较好，值得推广。

表3 基于BP-S模型的预测结果 m

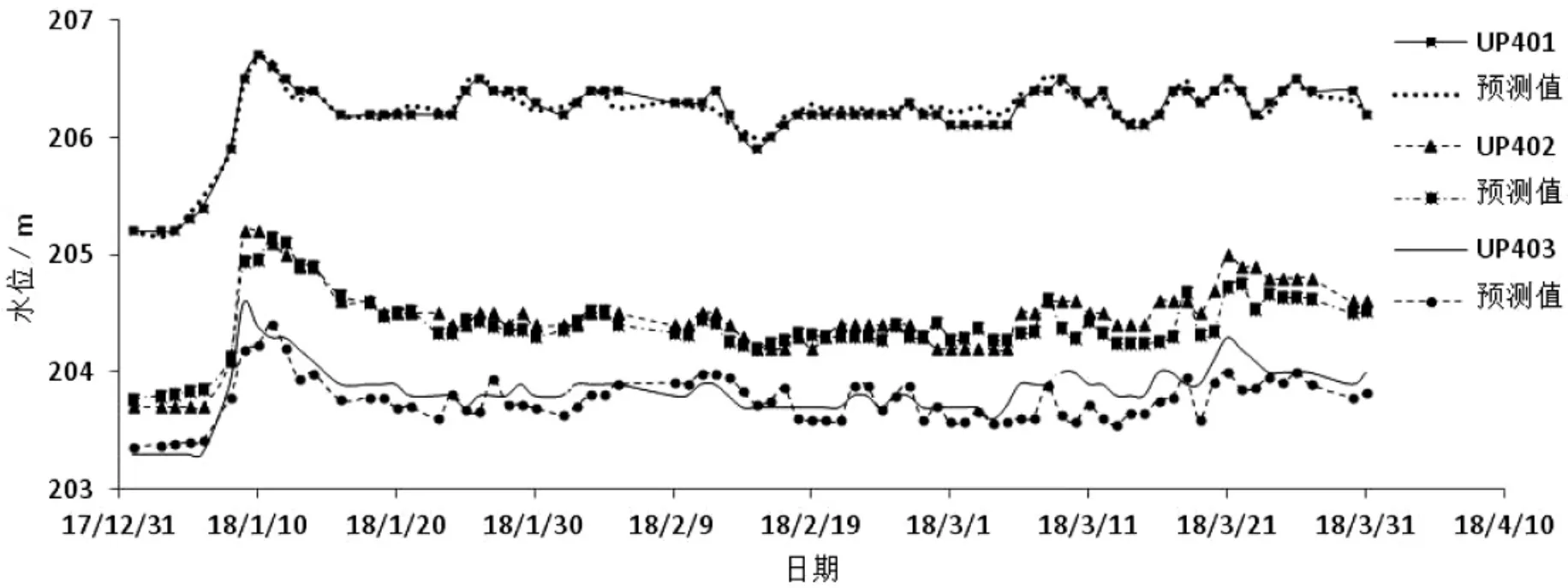
图3 BP-S模型的预测结果