含内热源的多孔方腔自然对流非正交MRT-LBM 模拟
2020-03-11张莹包进过海龙连小龙黄逸宸李培生
张莹,包进,过海龙,连小龙,黄逸宸,李培生
(南昌大学 机电工程学院,南昌330031)
多孔介质中的流体流动与传热在科学和工程领域有许多应用,如土木工程、地质力学、环境科学、生物工程、材料科学及再生热交换器、食品加工、电子设备冷却等其他相关领域[1-2]。因此,国内外许多学者对多孔腔体内流体流动及传热特性进行了深入研究,并取得了重要成果。邱伟国等[3]采用有限元方法对左侧部分多孔介质壁面方形封闭腔体内的自然对流传热进行了数值模拟。Yaacob和Hasan[4]采用有限差分的方法研究了倾斜多孔矩形方腔内的自然对流现象。
格子Boltzmann方法(LBM)作为近几年发展起来的一种介观数值模拟方法,与传统的宏观数值方法相比具有物理图像清晰、边界条件容易处理及并行性能好等优点[5-6]。因此,国内外许多学者采用LBM方法对多孔介质中的传热现象进行了数值模拟。Shokouhmand等[7]使用LBM 方法模拟了2个平行板之间的层流流动与对流传热问题。陆 威 等[8]基 于CLBGK (Coupled Lattice Bhatnager-Gross-Krook)模型,利用LBM 方法研究了顶盖驱动复合方腔内的双扩散混合对流现象,研究结果表明,多孔介质层对顶盖驱动复合方腔内的热质双扩散的影响十分显著。Huelsz和Rechtman[9]利用LBM 方法对倾斜方腔内的自然对流传热问题进行了模拟研究,分析了方腔倾斜角度及Rayleigh数对其流动与传热的影响。Zhao等[10]采用LBM方法研究了孔密度(孔尺寸)和孔隙率对自然对流的影响,结果表明,通过降低孔隙率和孔尺寸可以提高方腔内的整体传热效率。Bouarnouna等[11]采用多松弛格子Boltzmann方法(MRT-LBM)模拟多孔介质通道中的对流传热现象,表明Darcy数、Rayleigh数、多孔基材的厚度、导流板的厚度及位置对通道内的传热有着重要的影响。李培生等[12]采用非正交MRT方法对倾斜多孔方腔内自然对流进行数值研究,结果表明,方腔倾角对腔内传热影响很大,热壁面上平均Nusselt数随倾角的变化表现出M 型分布规律。
针对多孔方腔内流体流动与传热的研究,大多采用连续性的冷热壁面条件[13-15],然而在电子器件的冷却和建筑物的冷却等领域间断式的冷却方式有着广泛的应用。基于此,本文主要研究了含有内热源的多孔方腔的自然对流传热问题,对比了6种不同的冷源布置方案、内热源结构形式及内热源的位置对方腔内自然对流传热的影响,讨论了Darcy数、Rayleigh数等参数对方腔内流体流动与传热特性的影响。
1 物理模型的建立
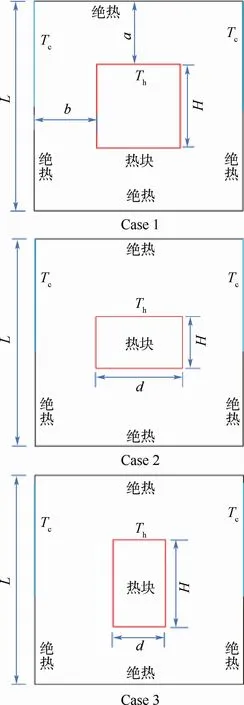
图1 物理模型Fig.1 Physicalmodel
图1为二维多孔方腔内含不同结构的内热源示意图,高温热块表面温度为Th,方腔左右壁面加粗蓝线表示低温壁面,温度为Tc,其余壁面均为绝热壁面。方腔内填充多孔介质为各向同性且均匀的材料。二维多孔方腔边长为L,对应于Case 1方形高温热块的边长为H,Case 2、Case 3高温热块高度为H,宽度为d,Case 1对应的H/L为0.4,Case 2、Case 3对应的H/L分别为0.3、0.5,d/L则分别为0.5、0.3,即使内置高温块的热边界周长相等。图2给出了Case 1对应内热源布置方式下的6种不同等温冷源边界的布置方案。
假设流体为不可压缩流体,忽略黏性散热,基于广义的非Darcy模型,多孔介质中的流体流动和对流传热在局部热平衡条件下的宏观控制方程为
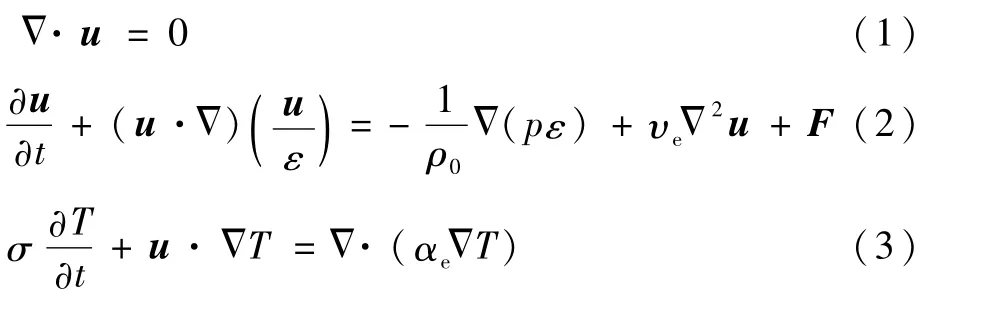
式中:ρ0为平均流体密度;u、T和p分别为流体平均速度、温度和压力;ε为孔隙率;υe为有效运动黏度;σ为孔隙间流体与多孔介质固体骨架之间热容比值;αe为有效热扩散系数;F=(Fx,Fy)为由多孔介质和其他外力引起的合外力项,可以表示为
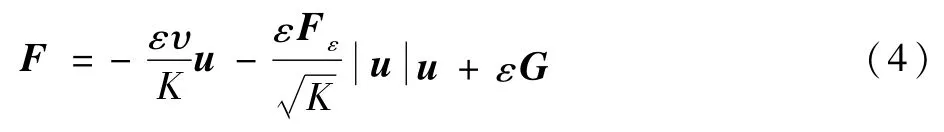
其中:等号右端的第1项、第2项、第3项分别为线性Darcy介质阻力、非线性Forchheimer介质阻力、浮升力;υ为流体的运动黏度;K为多孔介质的渗透率;Fε为几何函数;G为浮升力。
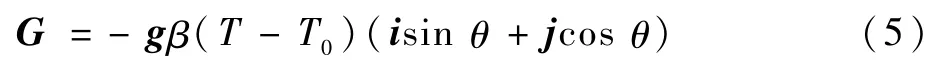
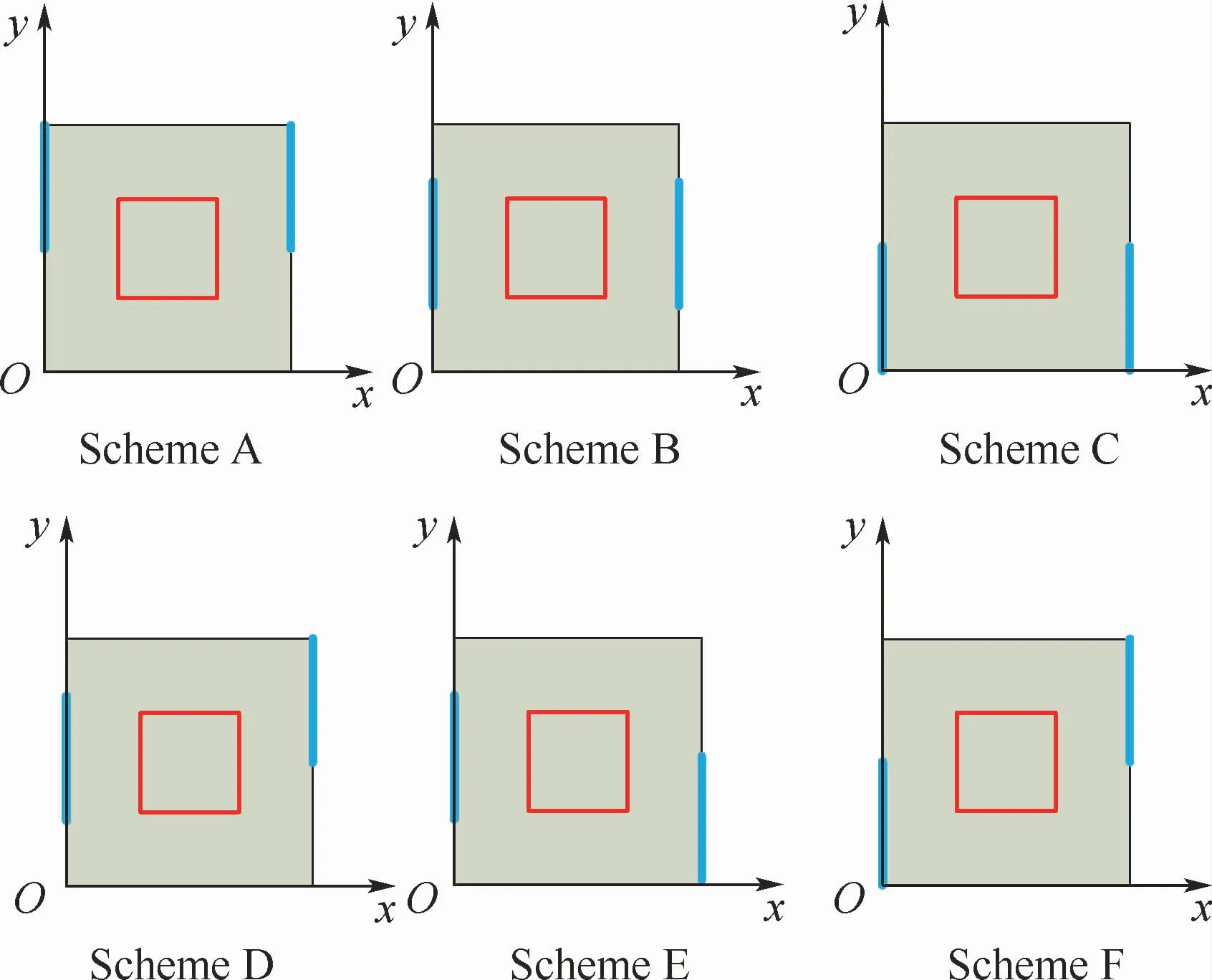
图2 六种不同等温冷源边界布置方案Fig.2 Six different isothermal cold source boundary arrangements
式中:β为热膨胀系数;g为重力加速度矢量;T0为参考温度,本文取为系统的平均温度;θ为方腔的倾斜角度,为0°;i为x轴的单位矢量,j为y轴的单位矢量。
方腔内置高温块热壁面上的平均Nusselt数Nuave的计算公式为
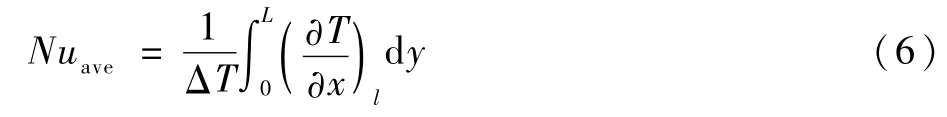
对于流体宏观流动涉及到的无量纲参数有:Da=K/L2,Pr=υ/αe,Ra=gβΔTL3/(υαe),J=υe/υ。其中,J为黏度比,温差ΔT=Th-Tc。
2 耦合双分布非正交MRT-LB模型
2.1 求解流场的M RT-LB模型
格子Boltzmann方程描述了气体分子分布函数的时空演变,通过宏观流动变量与分布函数之间的关系来得到宏观流动参数。非正交转换矩阵MRT-LB模型速度分布的演化方程为
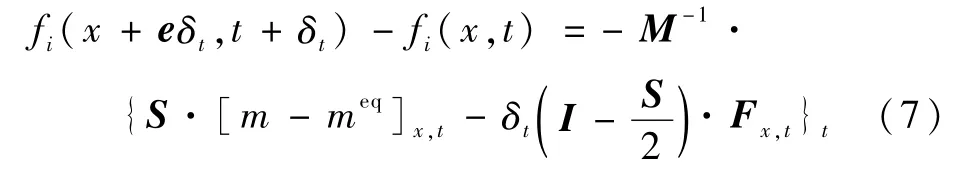
式中:e为离散速度的方向矢量;δt为时间步长;Fx,t为合外力;fi(x,t)为密度分布函数;M 为速度空间的非正交转换矩阵;S为对角松弛矩阵;I为单位矩阵;m和meq分别为f和feq对应的矩空间分布函数,其表达式为

对于二维多孔方腔内的流动,速度场采用D2Q9离散速度模型,各离散速度的方向矢量为
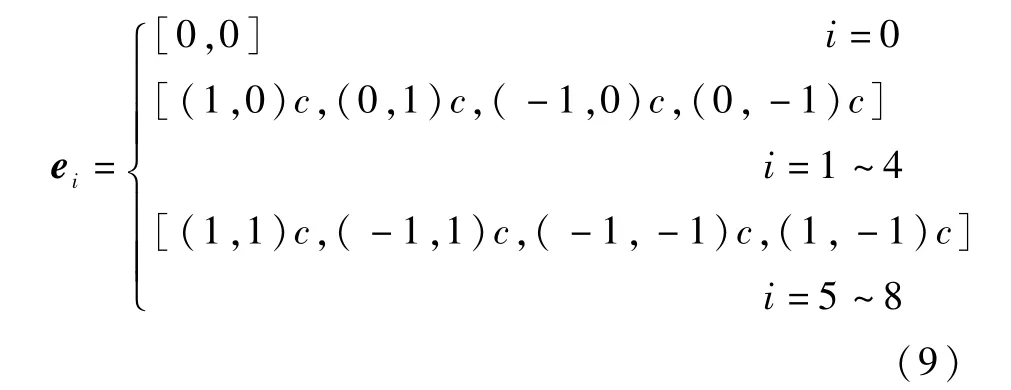
对于非正交转换矩阵M,可以表示如下:

对于矩空间平衡态分布函数meq,定义如下:
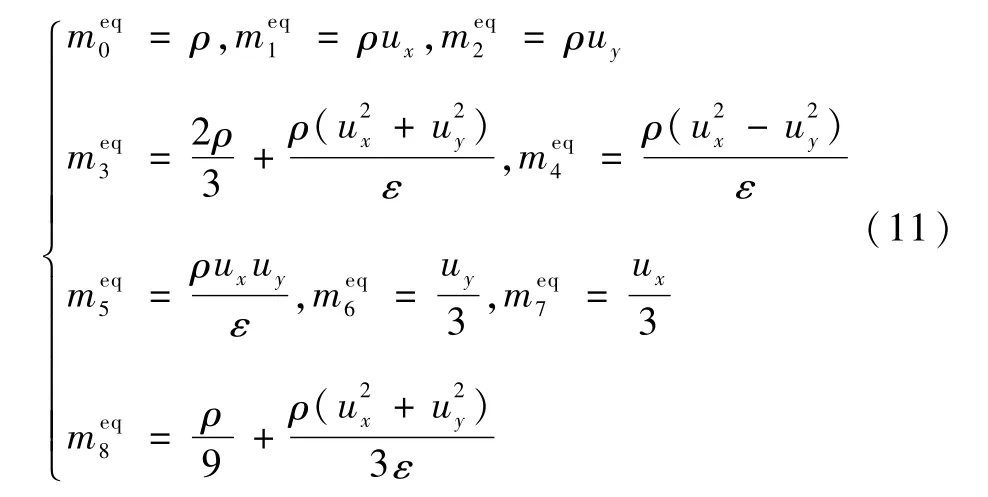
式中:ux和uy分别为u的水平分速度和竖直分速度;ρ为流体的密度。
速度场的平衡分布函数feq
i定义如下:
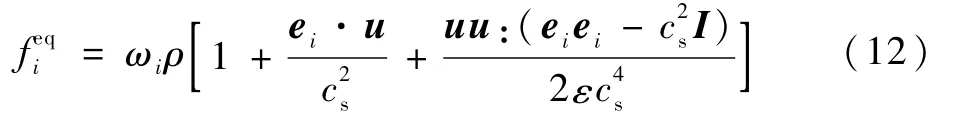

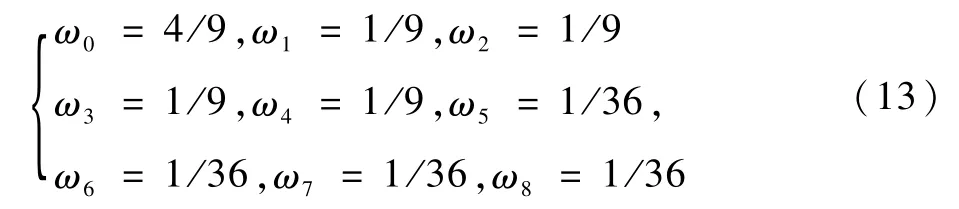
力项F定义如下:

本文所采用的MTR-LBM 方法分布函数的演化与常规的LBM 方法一样,首先是矩空间进行碰撞:
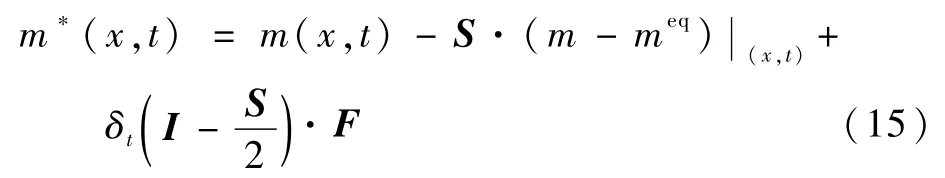
式中:m*为发生过碰撞后的矩空间分布函数。当碰撞完成后,通过公式f*=M-1·m*将矩空间转化为速度空间,迁移仍然在速度空间进行:
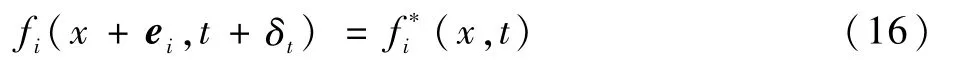
流体的宏观密度ρ和速度u定义如下:
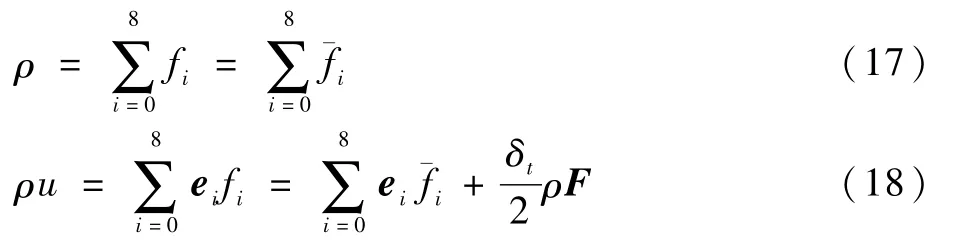
流体的宏观速度u可以通过引入一个临时速度v获得:

式中:

2.2 求解温度场的M RT-LB模型
在对温度场的求解时,采用计算量相对较小的D2Q5模型进行模拟,其模拟结果已经足够准确,二维温度场的非正交MRT-LBM方程定义如下:
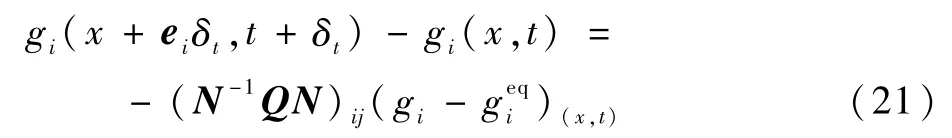
式中:g为温度分布函数;geq为温度平衡分布函数;Q为松弛系数矩阵;N为非正交转换矩阵,其表达式为
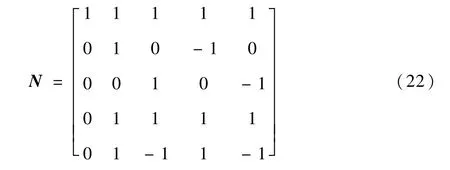
对于D2Q5模型,其温度场各离散速度的方向矢量为
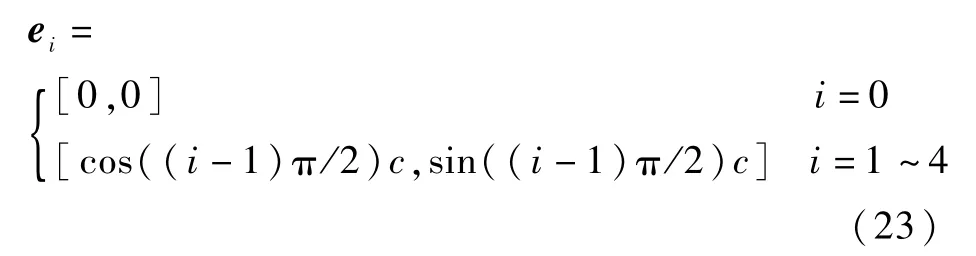
模型中的温度T通过式(24)计算:

矩空间平衡态分布函数neq为
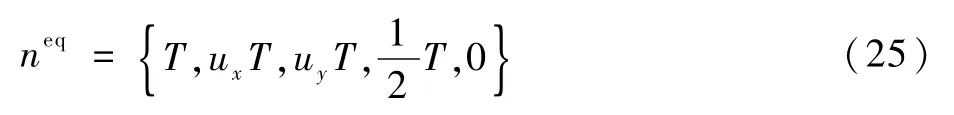
松弛系数矩阵Q定义如下:
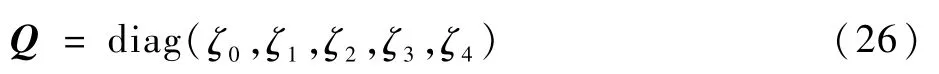
速度空间的温度平衡态分布函数geqi 定义为
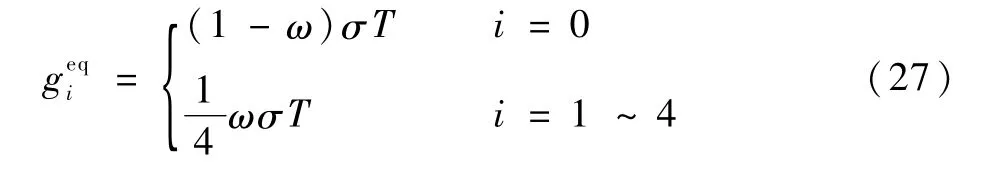
式中:ω为常值。
松弛时间τυ和τT公式如下:
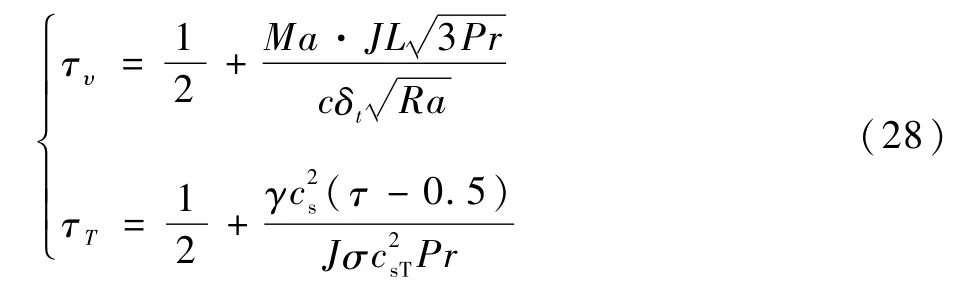
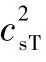
3 数值模拟结果及讨论
3.1 模型验证

图3 不同方法流线及等温线图比较(Ra=106,Da=10-4,ε=0.4,Pr=1.0)Fig.3 Comparison of stream lines and isotherms with different methods(Ra=106,Da=10-4,ε=0.4,Pr=1.0)
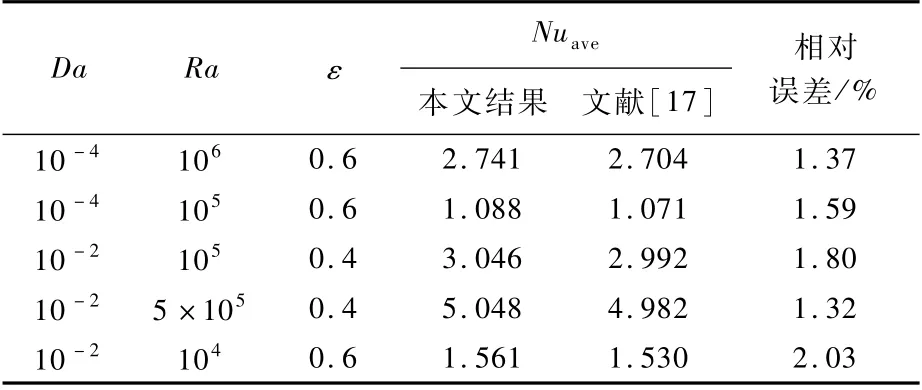
表1 热壁面上平均Nusselt数Table 1 Average Nusselt numbers at hot wall surface
3.2 冷源布置方案的影响
为了研究何种形式的冷却边界更有利于方腔内热量的传递,图4给出了ε=0.4、Ra=106、Da=10-2时所研究的6种不同冷源布置方案下方腔内温度场及流场变化图。图中:Ψmax,l、Ψmax,r分别表示左右漩涡的最大值。可以看出,在给定参数下,6种不同冷源布置方案等温线图差异很大,方腔内等温线只在冷壁面及热壁面附近的薄边界层内保持垂直,方腔中的等温线基本保持水平,表明此时腔内对流传热占主导地位。通过计算方腔内高温块热壁面上的平均Nusselt数及等温线图,部分冷源置于方腔上侧腔内的对流传热强烈,Scheme A、Scheme B、Scheme D的布置方案更有利于热量的传递。从流线图可以看出,Scheme C由于冷源空间结构的限制,导致方腔2个漩涡均集中于方腔的下部,流体的流动在方腔上部很弱,导致方腔上部的热量无法有效传递,方腔内整体传热效果很差。通过分析Scheme C、Scheme F两个布置方案,Scheme F布置方案热壁面Nuave及内热源右侧的漩涡强度明显高于Scheme C,表明提高冷源的布置位置能够明显提高腔内的对流传热强度。由流线图看出,方腔内产生2个流动方向相反的漩涡,分别位于内热源的左右两侧。由于6种不同的冷源布置方案,漩涡形状及涡心位置发生改变。冷源对称布置时,方腔内形成的2个漩涡也对称分布,方腔左右壁面冷源非对称布置时,2个漩涡不再对称分布,左右漩涡中心位置随冷源位置移动。
为了更直观地了解方腔内流体的流动特性,图5给出了ε=0.4、Ra=3×106、Da=10-2时6种不同冷源布置方案下方腔中间高度上的速度分布V。以高温块中心点为坐标原点,向右为速度的正方向。由图5知,在高温热块左侧速度首先达到负的最大值然后达到正的最大值,从而论证了方腔左侧形成的是逆时针运动的漩涡。Scheme A的布置方案方腔中间高度速度变化范围最大,而且其峰值最大,峰形更为尖锐,说明冷源双上部的布置方式流体具有很好的流动状态,对流传热作用强烈,Scheme C的布置方案其峰值最小,说明了双下部的冷源布置方案限制了方腔内流体的流动,腔内的传热效果很差。图6给出了ε=0.4、Ra=6×105时6种不同冷源布置方案下内热源热壁面上平均Nusselt数随Darcy数的变化。可以看出,Da<10-4时,热壁面平均Nusselt数随Darcy数的增大增加缓慢,表明方腔内的传热以热传导为主,此时Scheme B中部冷源的布置方案表现出最大的热壁面平均Nusselt数。Darcy数从10-4增加到10-3时,热壁面平均Nusselt数增幅剧烈,以Scheme B为例,平均Nusselt数从4.75增大到7.55,增大到原来的1.59倍。Darcy数增大到10-2后,随着Darcy数的增大,热壁面平均Nusselt数增加缓慢,在Da>10-2时,Scheme A布置方案热壁面具有最大的平均Nusselt数。这是由于Darcy数较大时,腔内流体流动受到的介质阻力较小,流动可以看做是纯浮升力的诱导流,方腔内的对流传热占据主导地位。
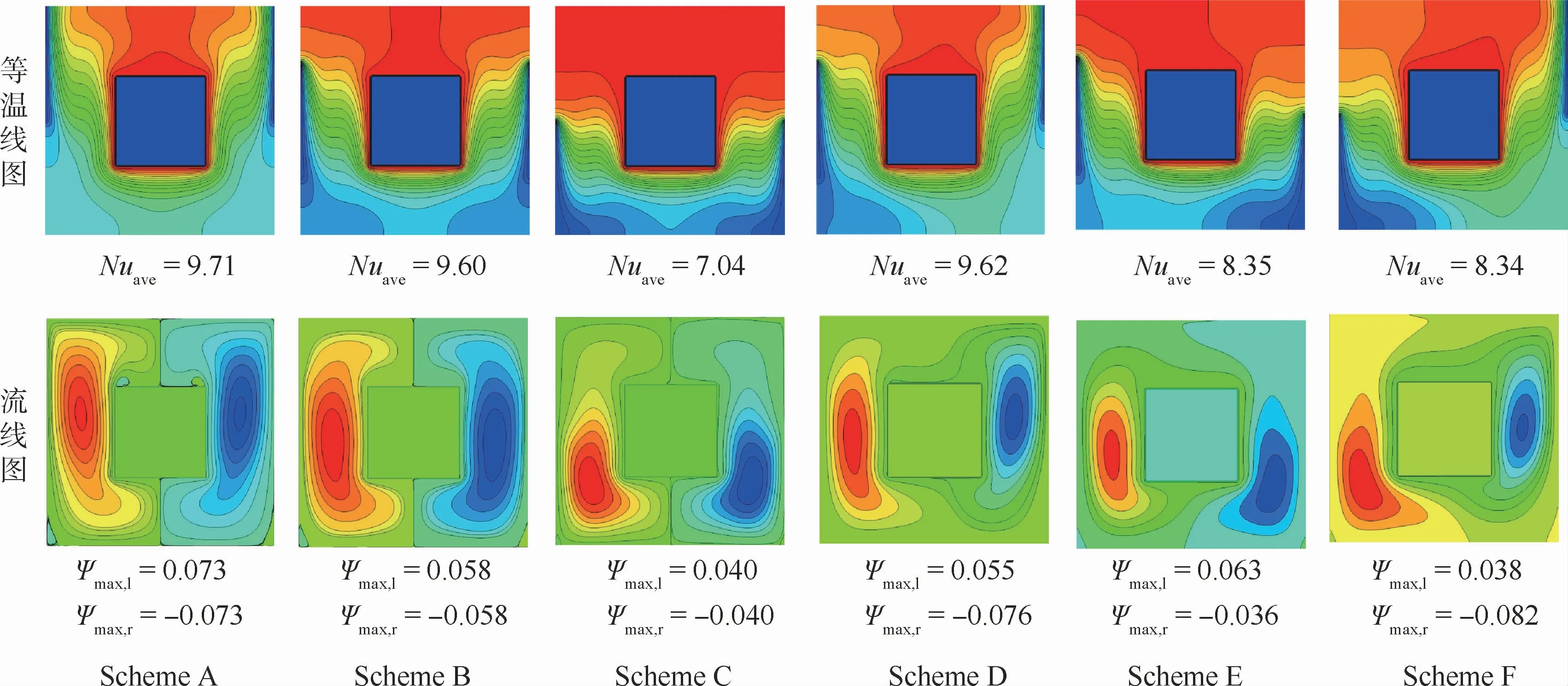
图4 六种不同等温边界布置下的等温线图和流线图Fig.4 Isotherms and stream lines for six different isothermal boundary arrangements
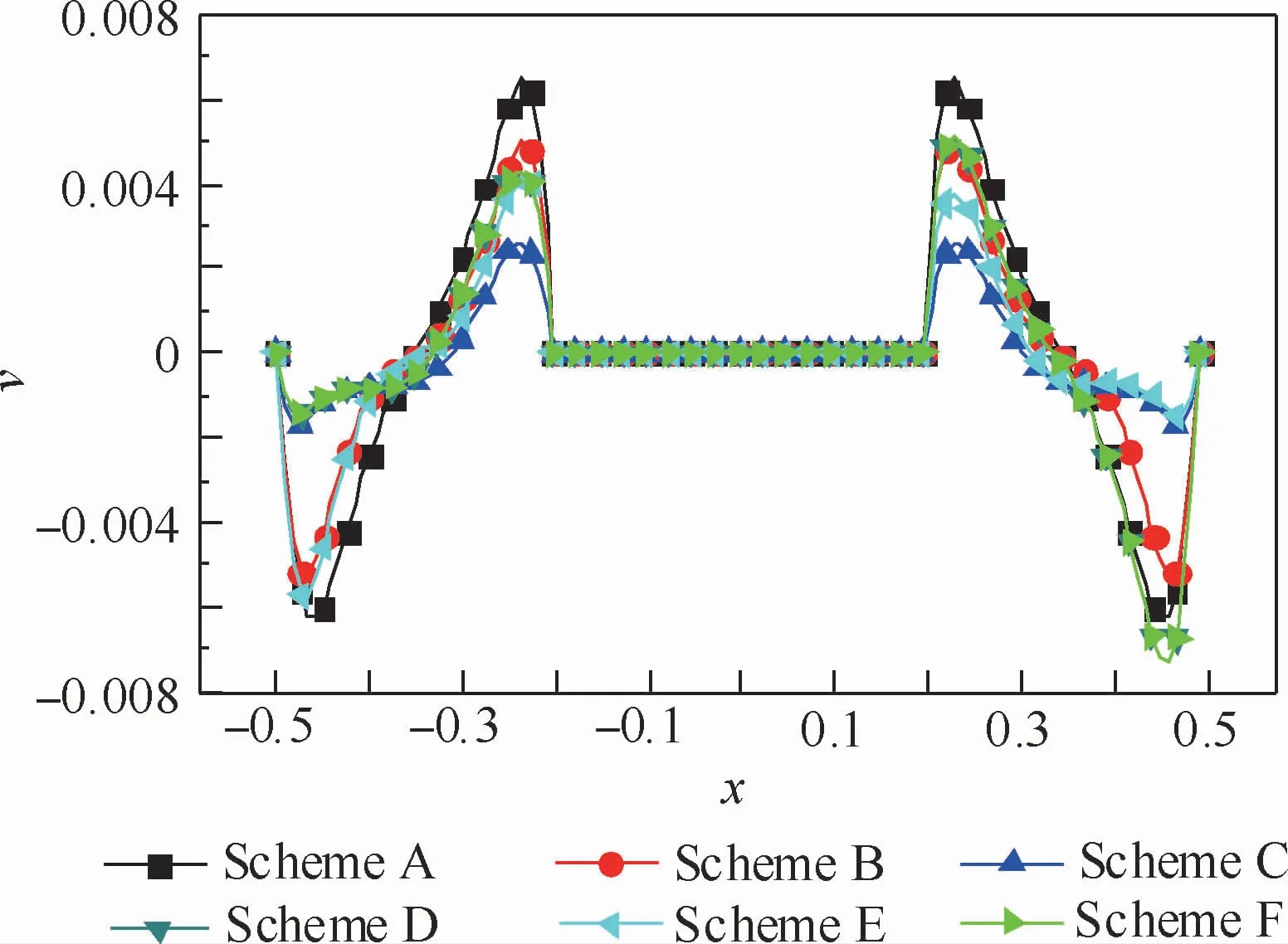
图5 六种不同等温边界布置下的速度分布Fig.5 Velocity profiles with six different isothermal boundary arrangements
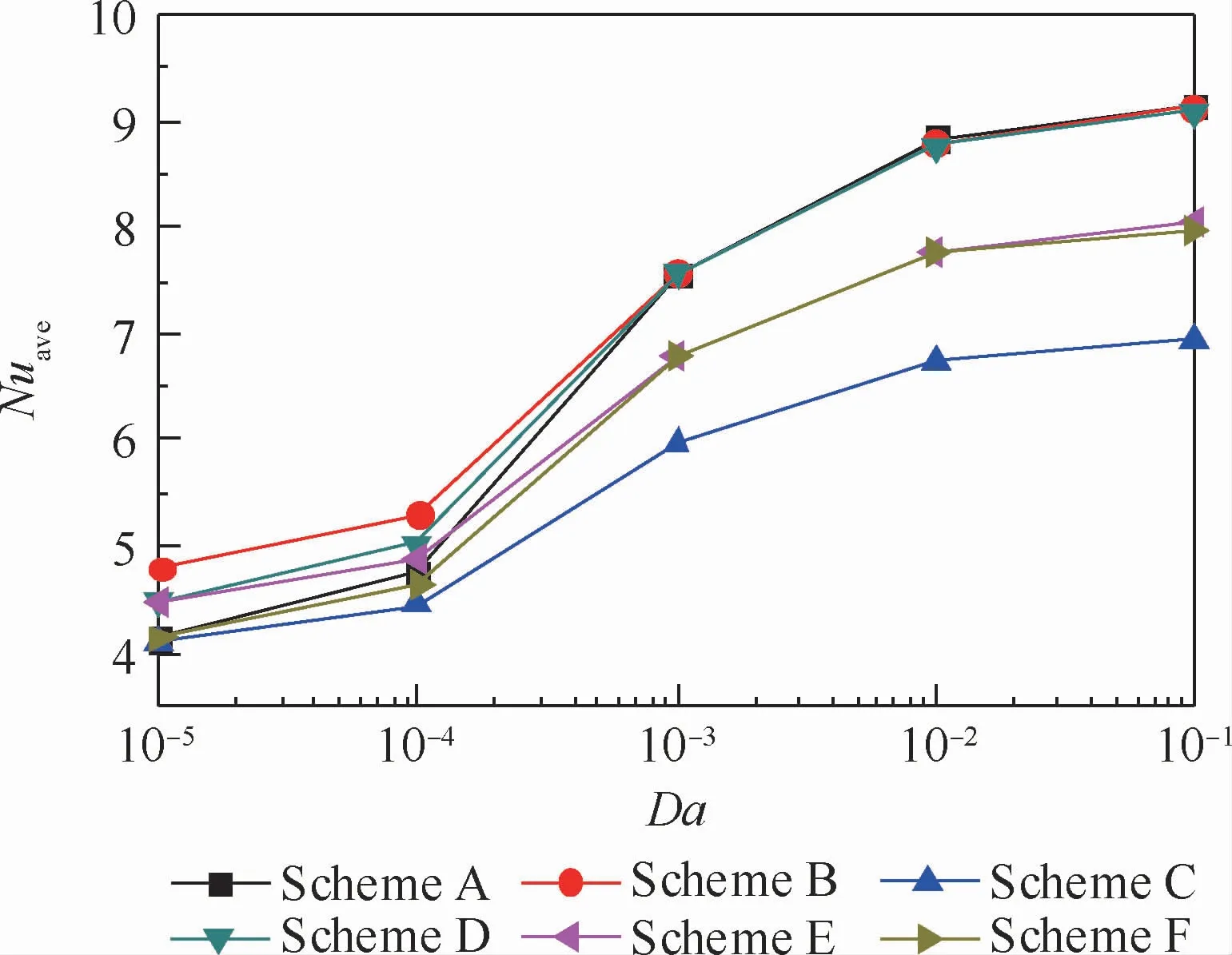
图6 六种不同等温边界布置下热壁面平均Nusselt数随Darcy数变化Fig.6 Variation of average Nusselt number at hot wall surface with Darcy number under six different isothermal boundary arrangements
3.3 Rayleigh数的影响
Rayleigh数作为影响方腔内自然对流传热的重要参数具有重要意义。当Ra<104时,方腔内传热以热传导为主,Ra=106时,对流传热已经占据主导地位。为了研究Rayleigh数对6种不同冷源布置方案下方腔内对流传热的影响,图7给出了ε=0.4、Da=10-2时,6种不同冷源布置方案下热壁面平均Nusselt数随Rayleigh数的变化情况。可以看出,Rayleigh数在1×106~6×106变化过程中,Scheme A的布置方案热壁面平均Nusselt数均为最大值,Scheme C冷源布置方案热壁面平均Nusselt数始终为最小值。Scheme A、Scheme B、Scheme D三种布置方案热壁面均有较高的平均Nusselt数,Scheme A热壁面平均Nusselt数从9.71增大到了14.49。图8给出了6种冷源布置方案下内热源热壁面上的局部Nusselt数变化情况,起始于内热源右壁面,随之左壁面下壁面,然后终止于内热源上部热壁面。可以看出,方腔内部等温块边角处的等温线聚集,表明此处有较大的温度梯度,局部Nusselt数在等温热块的边角出现尖峰。这可以从流体流动角度解释,由于热块边角不是流体流过的前缘就是后缘导致此处有较大的温度梯度。Scheme A的布置方案在内热源的左壁面、右壁面及上壁面均表现出最大的局部Nusselt数,解释了其有最大的热壁面平均Nusselt数。
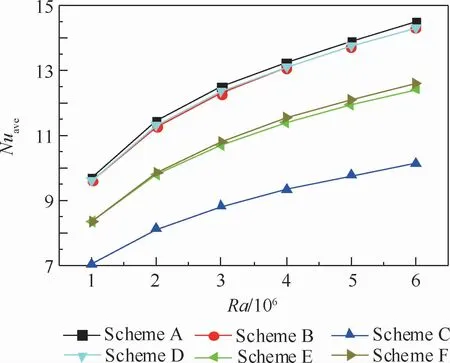
图7 六种不同等温边界布置下热壁面平均Nusselt数随Rayleigh数变化Fig.7 Variation of average Nusselt number at hot wall surface with Rayleigh number under six different isothermal boundary arrangements
3.4 内热源结构形式及位置的影响
为了研究方腔内放置何种形式的高温热块更有利于热量的传递,本节比较了3种不同内热源结构形式对腔内流体流动与传热的影响。3种模型内热源的热壁面周长相等,冷源布置方案为Scheme A采用的双上部冷却方式,图9给出了ε=0.4、Ra=3×105时不同Darcy数下3种不同形状的内热源的等温线图和流线图,流线图给出了漩涡的最大流函数值,等温线图给出了热壁面上平均Nusselt数值。由图9可以看出,Da=10-3时,3种方案的等温线分布均较为均匀,等温线大都垂直分布,表明此时腔内的传热是导热占主导地位,当Da=10-2时,腔中的等温线开始发生明显弯曲,只有冷边界与热块薄边界层内等温线保持垂直状态,这是由于Darcy数较大,腔内多孔介质的渗透率增大,流体受到方腔内部介质的阻力减小,腔内的对流传热作用增加,更有利于腔内的传热。由图9看出,在高Darcy数下,腔内垂直布置的内热源热表面具有最大的平均Nusselt数值并且最大流函数值亦为最大,表明在此条件下Case 3内热源的布置方式更有利于方腔内的散热。
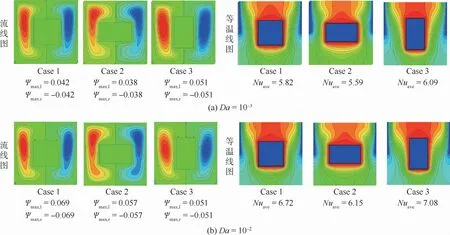
图9 三种不同内热源结构形式下方腔内的流线图和等温线图Fig.9 Stream lines and isotherms in square carity under three different internal heat source structures
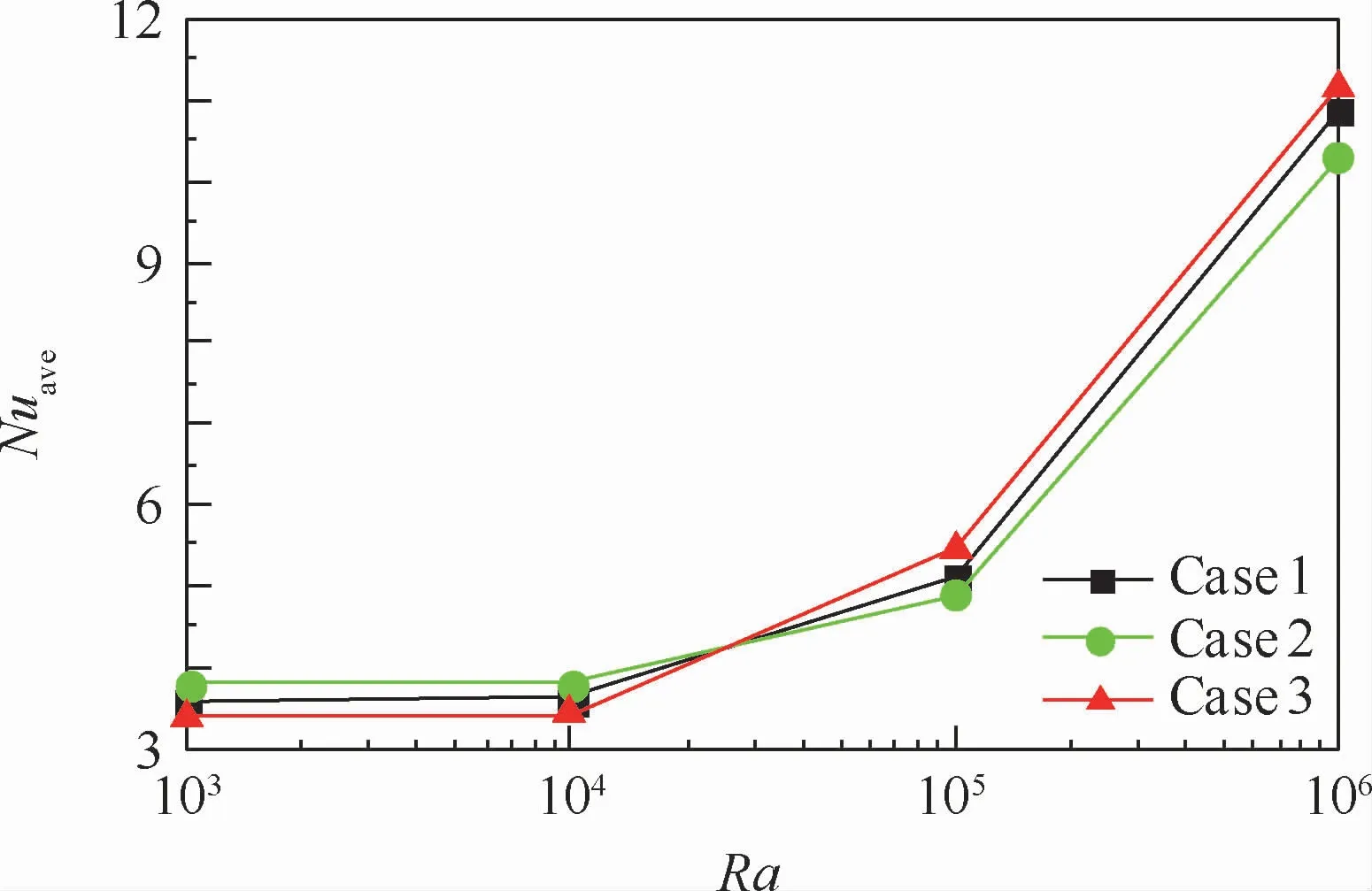
图10 三种不同内热源结构形式下热壁面平均Nusselt数随Rayleigh数变化Fig.10 Variation of average Nusselt number at hot wall surface with Rayleigh number in cavity under three different heat source structures
图10给出了3种不同内热源结构形式下热壁面上平均Nusselt数随Rayleigh数的变化情况。当Ra<104时,热壁面上平均Nusselt数增加缓慢,此时腔内以导热为主,且水平放置的高温热块(Case 2)方腔热壁面具有更大的Nusselt数。当Ra>105时,热壁面上平均Nusselt数随Rayleigh数增加剧烈,表明方腔内流体的对流传热作用在加强,在高Rayleigh数下,竖直放置的高温热块(Case 3)腔内具有更好的对流传热特性。为了更好地说明在高Rayleigh数下3种不同内热源结构形式下方腔内的对流传热效果,图11给出了ε=0.4、Ra=106、Da=10-2时,3种不同内热源结构形式下方腔中间高度上的速度分布v。以热块中心为坐标原点,向右为速度正方向,图中y=0.5为方腔中间高度的水平线,由于边界条件及内热源的对称布置方腔中间高度上的速度分布v亦表现出对称特性。由图11可以看出,Case 3内热源结构形式具有速度的最大值,Case 2结构形式峰值最小,Case 3结构形式流动覆盖范围更广,腔内具有更好的传热特性。
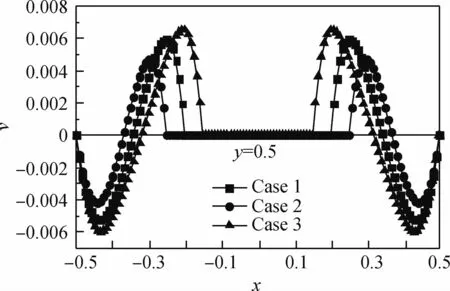
图11 三种不同内热源结构形式下的速度分布Fig.11 Velocity profiles in cavity under three different internal heat source structures
为了研究内热源位置对多孔方腔内流体流动及传热的影响,选取了H/L=0.4的高温热块为研究对象(即Case 1),高温热块上壁距离方腔上壁面的无量纲长度a,其他无量纲参数设置如下:ε=0.4,Da=10-3,Ra=106。图12给出了4种内热源处于不同位置时(高温热块中心始终处于方腔中垂线上),方腔内的等温线图和流线图。图中:左图为等温线图,右图为流线图。由图12可以看出,a=0时漩涡集中于方腔上部,漩涡基本对下部不产生影响,腔内下部的传热效果极差,随着a值的增大,漩涡开始覆盖方腔下部,下部的传热得到明显提高。为了进一步理解内热源位置对腔内对流传热的影响,图13给出了a=0,0.1,0.2,…,0.6时,7种不同内热源位置热壁面局部Nusselt数的变化。热壁面起始于左壁面,向右依次为右壁面、上壁面,终止于下壁面,横坐标表示热壁面的无量纲长度。由于内热源及冷源的对称布置,由图13看出内热源的左右壁面局部Nusselt数均相同,a=0时左、右热壁面的局部Nusselt数始终最小,下部热壁面则具有较大的局部Nusselt数。a=0.6时,内置热块左壁面、右壁面、上壁面均表现出最大的局部Nusselt数值。图14则给出了内热源热壁面上平均Nusselt数随无量纲长度a的变化。图中:散点表示模拟结果,曲线是运用最小二乘法得到的关于Nusselt数的拟合关系式的曲线,拟合度为91.1%,拟合的曲线关系式为:Nuave=7.73e0.99a-1.67a2。可以看出,随着无量纲长度a的增大,热壁面上的平均Nusselt数表现出先增大后减小的趋势,并且在a=0.25处,热壁面上的平均Nusselt数达到最大值,此时方腔内的对流传热水平最为强烈。

图12 不同a值下方腔内的等温线图和流线图Fig.12 Isotherms and stream lines in square cavity at different values of a
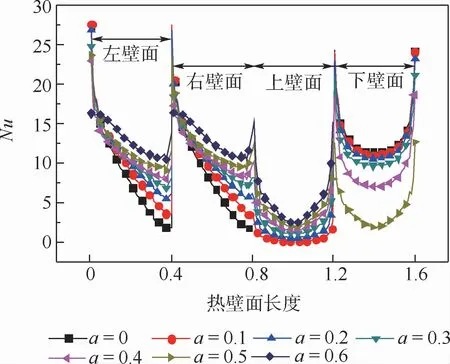
图13 不同a值下热壁面局部Nusselt数变化Fig.13 Variation of local Nusselt number at hot wall surface under different a values
为了研究方腔位于不同水平位置时(高温块中心点始终位于方腔水平线上),对腔内对流传热的影响,选取了H/L=0.4的高温热块为研究对象,高温热块左壁面距离方腔左壁面的无量纲长度b=0,0.025,0.05,…,0.6,其他无量纲参数设置如下:ε=0.4,Da=10-3,Ra=106。图15给出了不同b值下方腔内的等温线图和流线图,同时给出了热壁面上的平均Nusselt数及最大流函数值。图中:左图为等温线图,右图为流线图。可以看出,由于此时高温块的布置不再左右对称,腔内流线图亦表现出非对称性,b=0时腔内形成2个大小不一的漩涡,在高温块的上部形成一个逆时针运动的小漩涡,右侧形成一个顺时针运动的大漩涡。随着b值增加,由于方腔空间结构的改变上部漩涡开始向高温热块左侧移动,为了更好地理解b值对腔内传热的影响,图16给出了不同b值下方腔中间高度的垂直速度分布v。以热块中心为坐标原点,向右为速度正方向,图中y=0.5表示方腔中间高度的水平线,可以看出,在b由0增大至0.3的过程中,腔内左侧速度峰值亦依次增大,在高温块的右侧不同b值下的速度分布大致相同且峰值相差不大。
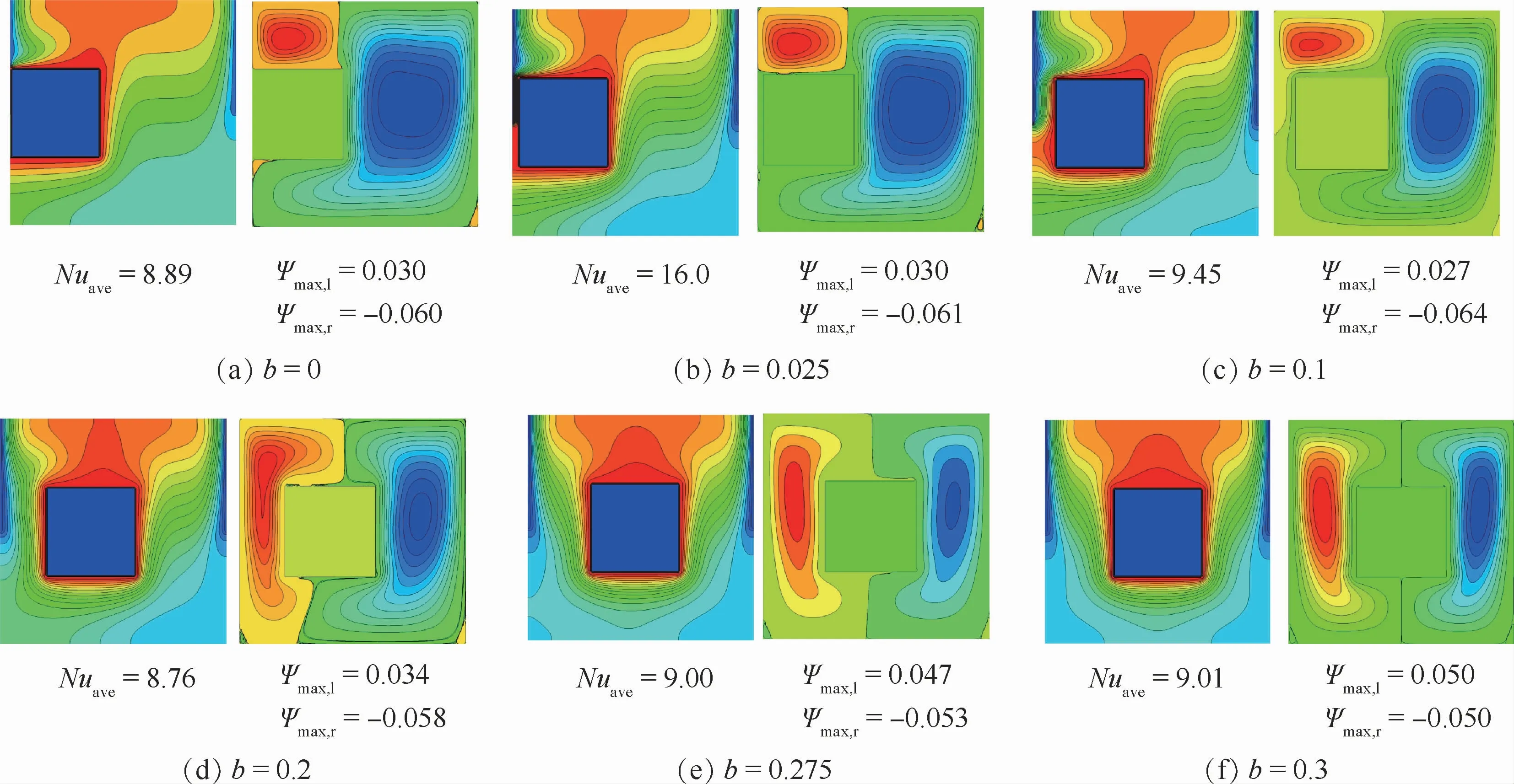
图15 不同b值下方腔内的等温线图和流线图Fig.15 Isotherms and stream lines in square cavity at different values of b
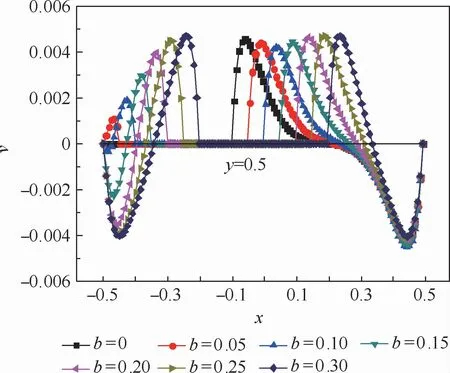
图16 不同b值下方腔水平中平面的速度分布Fig.16 Velocity profiles in the horizontalm id-p lane of square cavity under different b values
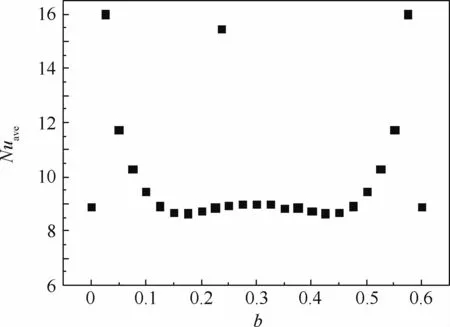
图17 热壁面平均Nusselt数随b值变化Fig.17 Average Nusselt number at hot wall surface versus b values
为了进一步研究内热源位于不同水平位置对腔内自然对流传热的影响,图17给出了方腔热壁面上平均Nusselt数随无量纲距离b的变化,同时图18亦给出不同b值下方腔热壁面上的局部Nusselt数变化。可以看出,热壁面平均Nusselt数随b的变化表现出对称分布,对称轴为b=0.3。因此只讨论0≤b≤0.3,在b从0增大的过程中,热壁面平均Nusselt数首先突增,在b=0.025处达到最大值,为16.0,随后平均Nusselt数开始减小,在b=0.15处达到最小值8.68,随后在b增大到0.3的过程中,热壁面上的平均Nusselt数又表现出上升的趋势。此现象可以从图18热壁面上的局部Nusselt数变化得到解释,在b=0.025时由于冷热壁面距离较近,高温热块左壁面上部附近存在极大的温度梯度,导致热块左壁面上侧具有很大的局部Nusselt值,且高温热块上部也有很大的局部Nusselt数,使得平均Nusselt数很大。b=0.15时,高温热块热壁面的右壁面和下壁面的局部Nusselt均表现出较小值,且另外2个热壁面的局部Nusselt数处于中间水平,导致平均Nusselt值很小。
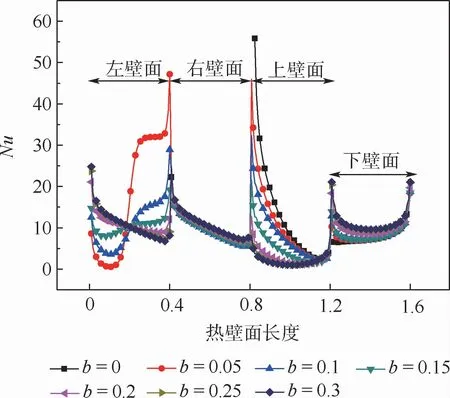
图18 不同b值下热壁面局部Nusselt数变化Fig.18 Variation of local Nusselt number at hot wall surface under different b values
4 结 论
本文采用非正交MRT-LBM对含内热源的二维多孔方腔内的自然对流传热进行了数值模拟,研究了不同冷源布置方案、Darcy数、Rayleigh数、内热源结构形式及其位置对方腔内对流传热的影响。研究结果表明:
1)当方腔内冷却边界及内热源左右对阵布置时,腔内温度场、流场亦左右对称分布。
2)对于讨论的6种冷源布置方案,双顶部布置方式在高Rayleigh数下有更好的冷却效果。
3)在高Rayleigh数下,垂直放置的内热源腔内具有更好的传热效果。
4)当高温方形热源尺寸H/L=0.4为定值时,高温热源位置a对腔内的对流传热影响显著,随着a值的增大,热壁面平均Nusselt数表现出先增大后减小的趋势,且存在最佳的位置(a=0.25),使方腔内的对流传热效果最强。
5)当高温方形热源尺寸H/L=0.4为定值时,高温热源位置b亦对腔内的对流传热有着重要影响,在b从0~0.3变化过程中,热壁面平均Nusselt数呈现出先增后减再增的趋势。
