HSPF在热带沿海流域水文模拟中的应用

桂晗亮, 张春萍,, 武治国, 张家铨

(1.武汉工程大学 光电信息与能源工程学院, 湖北 武汉 430000; 2.武汉新烽光电股份有限公司, 湖北 武汉 430000)

近些年来，随着城市工业化进程的加快，环境受到人类活动影响的程度不断加剧，其中水环境问题日渐严重，人类在享受工业化所带来的效益同时，不得不开始重视水环境问题。流域水文模型具有成本低、便于情景分析等优点，现被广泛用于水文分析计算、生态保护等方面[1]。而流域水文模型可按对流域水文过程描述的离散程度分为：集总式、分布式和半分布式[2-3]。由于流域模拟问题的复杂性等原因，使得半分布式模型在实践的过程中具有更广阔的应用前景和更大的推广价值。而HSPF(hydrological simulation program-Fortran)模型作为半分布式模型的经典代表，国外对于HSPF模型的应用已经非常广泛，研究者[4,9,13,23-24]利用HSPF模型对降雨径流为主的水文过程、气候变化以及土地利用变化对水文过程的影响开展了很多研究。Ourania Tzoraki等[5]利用HSPF模型模拟喀斯特流域的水文过程。Diaz-Ramirez等[6]的研究则表明，HSPF能够适用于热带岛屿河流流域水文模拟。Luo C.等[24]通过HSPF模型模拟土地利用的变化对Xitiaoxi流域水文水质的影响。然而HSPF模型在国内的关注和应用却很少，近年来才陆续有研究将该模型应用于丘陵地区太湖流域[7]、半干旱地区妫水河流域等[8]，但鲜有研究证实该模型在热带沿海流域的适用性。此外，也有学者对于HSPF模型的不确定性问题进行了深入研究，Igor Iskra等[9]利用蒙特卡洛—拉丁超立方(MC-LHS)、响应面和矩估计3种方法对HSPF进行了不确定性分析。程晓光等[8]利用GLUE-MC方法证实了HSPF模型不确定性与径流量有关。而庞树江等[10]利用CLUE分析HSPF模型的不确定性，并提出不确定性大小存在季节差异性。但是，对于降雨量影响模型不确定性的研究却很少见。

因此，为进一步探究HSPF模型在不同地区的适用性和不确定性的影响因素。本研究通过建立热带沿海地区三亚河流域的HSPF水文模型，选取2017—2019年3 a的径流量进行模拟，探究HSPF模型的敏感度以及不同降雨量条件下模型的不确定性，以期为HSPF模型在不同流域和地区的应用提供参考和依据。

1 研究区域与方法

1.1 研究区域概述

三亚河位于三亚市南部，由六罗水、水蛟溪、半岭水三条河组成，以六罗水为主流。三亚河由北向南穿城而过，经由三亚港入海。地理位置位为109°28′—109°31′E，18°14′—18°22′N，总流程28.8 km，流域面积337 km2。气候为热带海洋性季风气候，年平均温度为25.7 ℃，年平均降雨量为1 347.5 mm，且降雨主要集中在7—11月。土地利用类型包括林地、农业用地、城市用地和草地。

1.2 模型架构

建立水文模型输入的数据包括时间序列WDM数据(气象、水文数据)和GIS数据(地形DEM、土地利用数据)(详见表1)。利用BASINS模型所嵌套的WDMUtil软件将气象和水文数据整合成时间序列WDM文件，同时通过BASINS和GIS软件分别进行流域的划分(泰森多边形法)和边界的提取，将三亚河流域划分为28个子流域，HSPF建模需要的地理数据，由BASINS向WinHSPF转化，进而生成WinHSPF的UCI运行文件，并利用PEST软件对模型参数进行寻优。

表1 三亚河流域建模数据内容

模型的率定和验证是水文预报模型中必不可少的部分。研究采用纳什系数(NSE)和相对误差(Re)对模型拟合程度进行评价，NSE越接近1，Re越接近0，说明模型拟合的程度就越好。

(1)

(2)

1.3 参数敏感度分析

参数敏感度分析是研究参数变化所引起的模型响应，是模型不确定性分析的重要内容[11]，也是进行不确定性分析的前提工作之一。而HSPF模型水文模块的参数众多，且大部分参数具有物理背景，因此为提高不确定性研究的效率，需要先通过参数的敏感度分析，筛选出水文模块中对模拟有影响的参数。基于扰动分析法的Morris筛选法是目前应用较广的一种敏感度分析方法[12]。本研究采用修正的Morris筛选法，自变量以固定步长变化(±20%，±15%，±10%，±5%)，运用公式(3)计算出Morris系数的平均值用以评价参数的敏感度大小。

(3)

式中：S为参数相对敏感度(0≤|S|<0.05,不敏感； 0.05≤|S|<0.2,一般敏感； 0.2≤|S|<1,敏感； |S|≥1,极敏感)；Yi，Yi+1为模型第i,i+1次运行输出值；Y0为参数率定后计算结果初始值；Pi，Pi+1为第i，i+1次模型运算参数值相对于率定后参数值的变化百分率；n为模型运行次数。

HSPF模型包括3个主要模块：PERLND(透水区)，IMPLND(不透水区)和RCHRES(河道)，其中IMPLND模块仅分析地表径流，而PERLND模块主要分析地表径流、壤中流和地下水水文过程。模型自上而下分为树冠层、植被层、各土壤层(包括表层土壤、上土壤层、下土壤层、地下水涵养层)，降雨在6个垂直的存储层进行分配，最终进入河道[7]。研究主要通过HSPF的水文模块模拟三亚河流域的径流量，结合相关研究[11,13-15]，选取对HSPF水文模块有影响的8个参数及其取值范围(表2)，利用修正的Morris筛选法，计算各参数在该流域的相对敏感度。

表2 对HSPF水文模块有影响的参数敏感度分析

1.4 MC-LHS分析方法

MC-LHS方法是将蒙特卡洛(Monte-Carlo, MC)模拟和拉丁超立方抽样(Latin hypercube sampling, LHS)结合的一种不确定性分析方法。蒙特卡洛方法则是一种以概率统计理论为基础的数值分析方法，常用于解决确定性和不确定性问题[3]。蒙特卡洛模拟的主要步骤分为： ①对输入参数范围内随机抽样； ②将随机抽样结果代入模型运行； ③对运行结果进行统计分析。但是，蒙特卡洛模拟中的随机抽样往往不能保证参数的抽样点服从均匀分布，且需要非常庞大的样本量，而基于分层随机抽样的拉丁超立方抽样能够使样本的覆盖率更好，同时能减少抽样次数[16]。因此将拉丁超立方抽样与蒙特卡洛结合起来的MC-LHS方法用于模型不确定性分析的效率更高。本研究以纳什系数为目标函数，选取敏感度分析结果中的参数，采用拉丁超立方抽样取得500个样本，代入HSPF模型中运行并计算纳什系数，通过公式(4)—(5)对目标值纳什系数进行区间估计和变异系数计算。

(4)

(5)

式中：X为目标值；E(X)，D(X)分别为随机变量X的数学期望和方差；ε为任意给定的正数；Cv为变异系数； SD， MN分别表示随机变量X的标准偏差和均值。

2 结果与分析

2.1 模型率定与验证

研究选用三亚河流域2017—2019年日径流量为模拟对象，其中2017年1月1日至2018年12月31日为率定期，2019年1月1日至2019年12月31日为验证期，选用纳什系数和相对误差来评价模型拟合程度，结果详见表3。结合图1的模型拟合过程线，率定期和验证期的纳什系数分别为0.93和0.98，相对误差分别为0.87%和0.21%，就水文模型模拟而言，一般认为纳什系数大于0.90和相对误差小于10%就表明模型模拟的效果很好[17]。从率定期和验证期模型拟合的结果来看，建立的HSPF模型对于日时间步长的径流量拟合程度很好。为进一步验证模型的适用性，将模型用于月时间步长的径流量的模拟，如表3和图1所示。结果说明HSPF模型适用于不同时间步长沿海热带流域的模拟，能够较为真实地反映实际水文过程。

表3 HSPF模型率定和验证的模拟结果

图1 不同时间步长降雨径流过程线及散点图

2.2 参数敏感度分析结果

以模型拟合程度指标NSE为目标值，利用修正的Morris筛选法计算参数敏感度(表2)。分析表2可知，参数敏感度依次为：AGWRC，LZSN，INFILT，INTWF，UZSN，IRC，LZETP和DEEPFR，其中相对敏感度较大的参数为AGWRC，LZSN，INFILT和INTWF，AGWRC的相对敏感度为-0.69(敏感)，LZSN的相对敏感度为-0.05(一般敏感)，INFILT和INTWF的相对敏感度为-0.04，余下参数的相对敏感度较低。

AGWRC是地下水消退系数，控制地下水的退水过程进而影响产流量；LZSN是下土壤层的额定蓄积，主要影响河道入流量[18]。HSPF降雨汇流过程主要是由地表径流、壤中流和基流组成，热带流域独特的气候条件有可能影响土壤含水量、下渗率等特性，使得地表径流和壤中流在降雨汇流过程中的作用减弱，此时水文过程主要受基流影响。

HSPF模型的水文循环包括植被截留、地表径流、土壤水分配、地下水运动、蒸散发等部分。通过与国内外对HSPF模型水文模块参数敏感度分析的研究结论进行对比(表4)，发现HSPF模型参数敏感度的相对大小具有空间差异性，不同流域的敏感参数和相对敏感度大小并不完全相同，本研究中较为敏感的参数依次为AGWRC，LZSN，INFILT和INTWF，而其他研究[7,11]中敏感的参数更多。结合模型的水文机理分析，模型在不同流域的模拟中存在差异性[19]，可能与各流域不同的地形地貌、土地利用等条件有很大关系。例如，将本研究与半干旱半湿润的妫水河流域[8]进行对比，发现在参数的相对敏感度大小上就存在着很大的差异性，妫水河流域地处北温带，属于大陆性季风气候，地形多以丘陵为主，本研究中的热带沿海流域属于热带海洋季风性气候，多以城镇、山地为主，在地形地貌、气候、城镇化比例等方面明显的差异，能够影响地表径流和土壤层中的再分配过程。此外也有研究指出流域特征和气候特征等相似的流域之间，敏感性参数类似[20]。

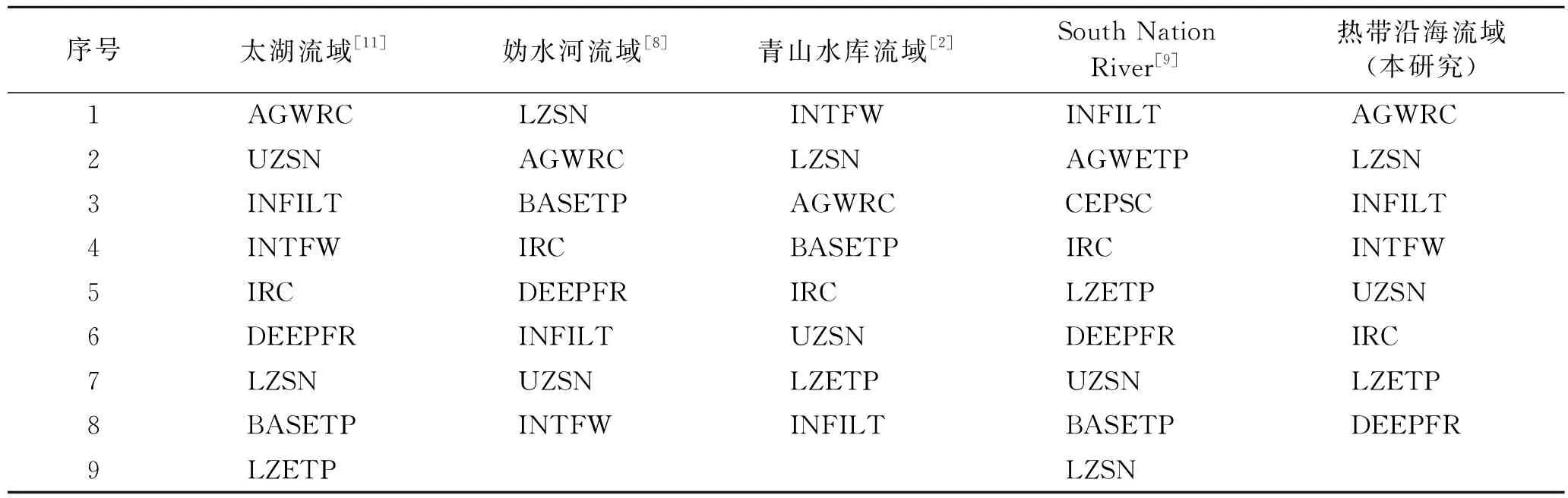
表4 国内外HSPF参数敏感度分析对比

2.3 不同降雨量对模型不确定性的影响

选取敏感参数进行拉丁超立方抽样并代入HSPF模型中运行，依据日降雨量划分成小雨(0～10 mm)、中雨(10～25 mm)、大雨(25～50 mm)和暴雨(50 mm以上)4种降雨类型，以模型拟合程度评价指标纳什系数为目标函数用于不确定分析，分别计算离散系数和置信水平为80%，90%下模型区间(表5)。由表5可知，4种类型降雨的Cv值分别为大雨(-11.268)、暴雨(-4.074)、中雨(0.104)、小雨(0.102)，说明HSPF模型对于不同降雨量模拟的不确定性存在差异，降雨量小的时段(≤25 mm)模型的拟合程度相比较降雨量大的时段(>25 mm)模型的拟合程度更好，且降雨量越大，不确定性越大，模型就越不稳定。分别对比置信水平为80%和90%下目标值的变化区间，模型区间也与降雨量有关，降雨量较小时(≤25 mm)不同置信水平下的变化区间远小于降雨量大时(>25 mm)。

表5 不同降雨类型HSPF不确定性计算结果

降雨量不同时，模型不确定性大小和区间有很大差异(图2)。图2表明HSPF模型的不确定性大小和降雨量有关。之所以出现这种情况，与HSPF模型的产流机制有关，模型中将透水地段水量平衡过程概化成净雨到达地表形成地表径流，产生入渗并实现各土壤层中的再分配，不透水地段水文过程为净雨产生地表径流的过程；降雨经地表植被和洼地截留后产生地表径流、壤中流和基流，落地雨在土壤中的再分配过程与雨强等因素密切相关。当雨量较小时，降雨大部分直接经过地表植被等截留后直接形成了地表径流，而少部分或没有净雨进入土壤中再分配，这时模型产流主要是地表径流，但是雨量较大时，模型的产流包括地表径流、壤中流和基流。因此，降雨量可用于解释其他研究[10]提出的HSPF模型不确定性的季节差异，同样在其他水文预报模型的研究中也证实了降雨量是影响水文模型不确定性的因素之一[21-22]。

3 结 论

(1) 通过HSPF模型对三亚河流域的日流量进行模拟，分别以2017和2018年的日径流量为率定期，2019年为验证期，率定期和验证期的纳什系数为0.93和0.98，相对误差为0.87%和0.21%。结果表明所建立的HSPF模型能够很好的模拟三亚河流域实际的水文过程。此外，进一步验证了HSPF模型对月时间步长的模拟，证实了在沿海热带流域的适用性。

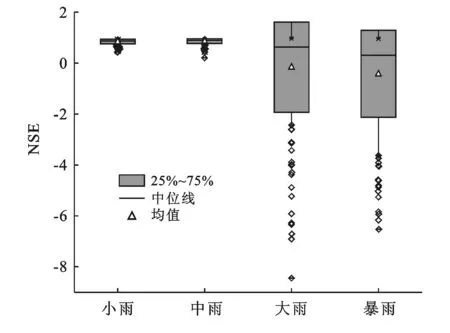
图2 不同程度降雨目标值箱线图

(2) 在HSPF模型完成率定的基础上，利用Morris筛选法对模型水文模块参数进行敏感度分析，三亚河流域对径流过程影响的敏感参数依次为：AGWRC，LZSN，INFILT，INTWF，UZSN，IRC，LZETP，DEEPFR，其中AGWRC最敏感，而LZETP和DEEPFR对该流域径流模拟几乎无影响；同时与国内外研究中的结论进行对比，发现参数敏感度在不同流域不同。

(3) 利用MC-LHS方法进行不确定分析，发现模型模拟的不确定性与降雨量之间相关性明显。降雨量越大，模型模拟的置信区间和变异系数Cv越大，模型的不确定性就越大，说明模型就越不稳定。同时证实了降雨量是影响HSPF模型不确定性的因素之一，进一步解释降雨量的变化是造成HSPF模型不确定存在季节差异性的原因之一。