HHT和马氏距离融合的船用空压机故障诊断

胡欢欢，王永坚，邱 晨

(集美大学轮机工程学院， 福建 厦门 361021)

0 引言

舶用二级往复式空压机是船舶压缩空气系统的关键设备，其工作性能的好坏对船舶正常营运将产生影响，开展船用空压机故障类型的有效识别和故障诊断具有良好的现实意义。船用二级往复式空气压缩机最常见的故障是一、二级缸套-活塞组发生断环，依靠空压机性能参数很难及时、准确地查找故障问题，本文提出一种基于振动信号分析的船用二级往复式空气压缩机活塞环断环故障诊断方法。由于空压机振源多且机械结构复杂，振动信号是非线性非平稳的，如何从此类信号中提取故障特征将是一件十分关键的工作。传统的振动信号处理方法在处理非线性非平衡信号时存在缺陷，如短时傅里叶变换因高低频要求不同的窗函数，合适的窗函数不易选取，Wigner分布会产生二次混叠，Cohen类很难选择合适的核函数，小波变换不具有自适应性，难以选择小波基[1-2]。希尔伯特-黄变换(hilbert-uuang transform，HHT)使用经验模态分解算法，将信号分解成一组本征模态函数[3-5]，此类函数具有单量自适应性，高时频分辨率和良好的时频聚集性的优点，故可以处理非线性非平稳信号。对重构后的信号进行希尔伯特变换，可以得到信号瞬时时频分布，进而可以得到Hilbert边际谱[6-7]，它可以准确地反映出信号幅值和频率之间的关系。马氏距离依据数据的协方差距离，具有良好的小样本分类特性，可以准确地反映两个样本的相似程度[8]，因此在机械故障识别领域得到广泛应用。

综上，本文提出一种把希尔伯特-黄边际谱和马氏距离融合的船用二级往复式空压机断环故障诊断方法，通过搭建实验平台(以船用应急空压机为实验对象)，人为模拟空压机三种状态类型(正常状态、一级活塞断环、二级活塞断环)进行实验，验证所提方法的有效性和故障识别的准确性。

1 信号分析方法

经验模态分解和希尔伯特变换及谱分析两个部分组成希尔伯特-黄变换(HHT)。经验模态分解(EMD)算法得到本征模态函数(IMF)必须满足一下两个条件：1)极值点和零点的个数相差不多于一个:2)极大值和极小值点的包络线的平均值等于零[5]。

EMD分解实测信号x(t)的步骤如下。

步骤一应用三次样条算法求振动信号x(t)所有的局部极大值、极小值点的包络线，即上、下包络线，然后求取这两个包络线的平均值，记为m1，将x(t)减去m1，得到h1=x(t)-m1。

步骤二如果h1满足上述的条件，那么h1就是第一个本征模态函数(IMF1)；如果h1不满足条件，则把h1作为原始数据，重复步骤一，即先得到上、下包络线的平均值m11,h1减去m11得到h11，再判断是否满足条件，如果不满足，则重复循环k次，直到h1k满足条件，并记c1=h1k为第一个本征模态函数，h1k=h1(k-1)-m1k。

步骤三把第一个本征模态函数c1从原始信号x(t)中分离出来，从而得到r1=x(t)-c1。

步骤四将r1当作原始数据，重复上面的三个步骤，得出x(t)的第2个满足条件的IMF分量c2(IMF2)。如此重复n次，得出x(t)的n个IMF分量，这样就有如下式子：

当余下的信号函数不再满足提取IMF分量的条件时，循环结束，余下的信号函数称为残余项rn。

于是原始信号x(t)可以表示为n个IMF分量和一个残余项rn之和，这样就重构了原始信号，即为：

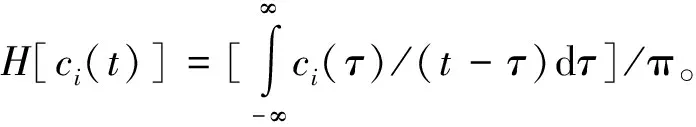
于是求得每一个IMF分量的幅值和相位函数分别为：

φi(t)=arctan [H[ci(t)]/ci(t)]。

进而求得瞬时频率ωi(t)=(1/2π)dφi(t)/dt。

由于残余项rn对重构原始信号影响较小，故省略不计，从而得到重构的原始信号为：

Re为实部，n为IMF分量的个数。由此式可以看出幅值ai(t)和频率ωi(t)都是时间t的函数，从而得到Hilbert谱，记为：

(1)

进而得在某一频段ω1～ω2的能量函数S为：

(2)

2 实验数据采集

本实验台选用应急船用往二级复式空压机，额定转速为2800 r/min,额定功率为7.5 kW,额定压力12.5 MPa;储气罐额定压力为12.5 MPa；采用东华测试公司的信号采集仪DH-5922，以及相关的DHDAS信号测试分析系统软件；传感器采用加速度传感器，最大可测加速度为50g m/s2，灵敏度为100.8，激励电压为24 V，谐振频率为30 kHz。

将4个加速度传感器分别安装于一、二级气缸盖顶端和一、二级缸套侧面中间的位置。搭建的实验平台如下图1所示。本次采用人为模拟故障问题实验，设正常状态、一级活塞断环、二级活塞断环3种故障，如图2所示。

采集正常状态下的振动信号，具体过程如下：开启DH-5922信号采集仪，再打开DHDAS信号测试分析系统软件，将采集频率调节到12 kHz,采样点数为25 600个，数据格式为TXT，后启动空压机，当空压机处于工作状态时，按下信号采集仪采集信号键，直到信号采集点数完成，停止采集信号，得到正常状态振动信号。将一级断裂的活塞环安装于对应的活塞上，重复上述采集信号的步骤，得到一级活塞断环的故障振动信号数据；同样可得二级活塞断环状态下的振动信号数据。本次实验每种状态各采集10组数据，共40组数据，三种状态共120组数据。

3 数据分析

将采集到的数据使用MATLAB2013b软件进行处理，得到三种状态下信号原始图，如图3所示。

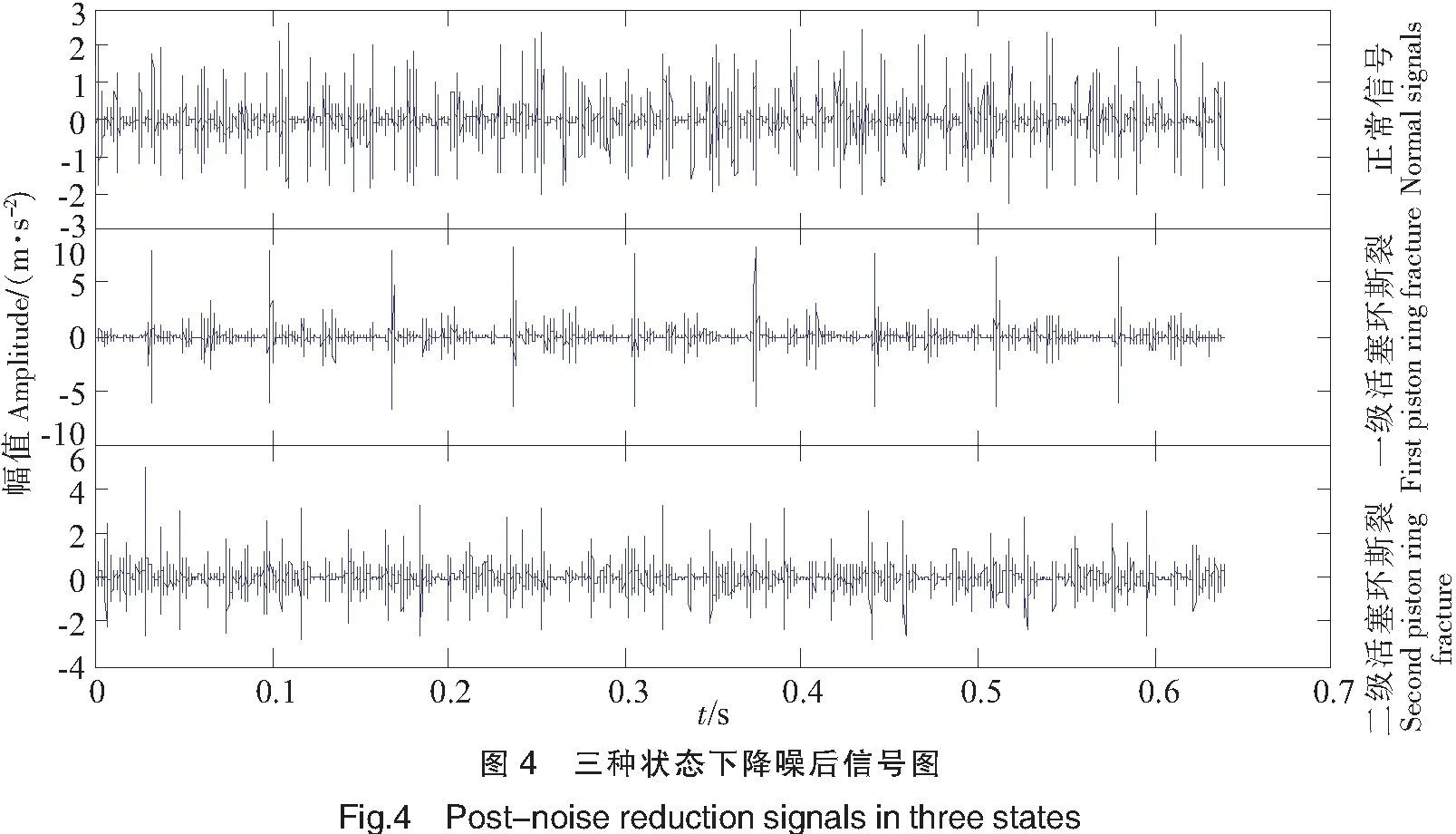
由图3能够得出，由于背景噪声和环境等因素的影响，所获取的三种状态下的信号存在着较多的干扰，这将严重影响故障诊断识别的准确性。因此，本文采用一维离散小波降噪方法对三种信号进行处理，小波降噪参数为：sqtwolog小波阀值，db6小波，6层分解[9-10]。降噪后的信号如图4所示。对比这两幅图片可以发现降噪后的信号混叠较小，故降噪后的信号噪声被明显抑制。

分别将正常状态，一级活塞断环，二级活塞断环三种状态下降噪后的信号数据使用EMD分解。列出三种状态下的前6个IMF分量函数图，正常状态如图5所示。

由于EMD算法的特性，不可避免地会出现虚假的IMF或者与原始信号关系不大的IMF分量，如何剔除这些分量关系着故障识别和诊断的准确性。由于每一个IMF分量都正交于原始信号，故可得每一个IMF分量与原始信号的相关性，这里用相关系数ρ来表示相关性，ρ越大表示ρ所对应的IMF分量与原始信号相关性越大。由概率论相关系数计算公式可得ρ：

其中i表示第i个IMF分量。

表1列出了三种状态下的前6个IMF分量与原函数的相关系数。由表1可知三种状态下的前5个IMF分量与各自原信号相关度较高，第6个相关度较低。由此可知第6及其以后的IMF函数由于相关度很低，故可以舍弃不计,于是得到5个敏感的IMF分量。

表1 前6个IMF分量的相关系数

对每种状态各个IMF分量使用希尔伯特变换重构原函数后得到其时间-频率-幅值三者间关系的希尔伯特谱，其时频三维图如图6所示。从图6可得原函数频率幅值较大的部分分布在0～5 000 Hz之间，故信号的能量也是大部分分布在这个频率区间之中。

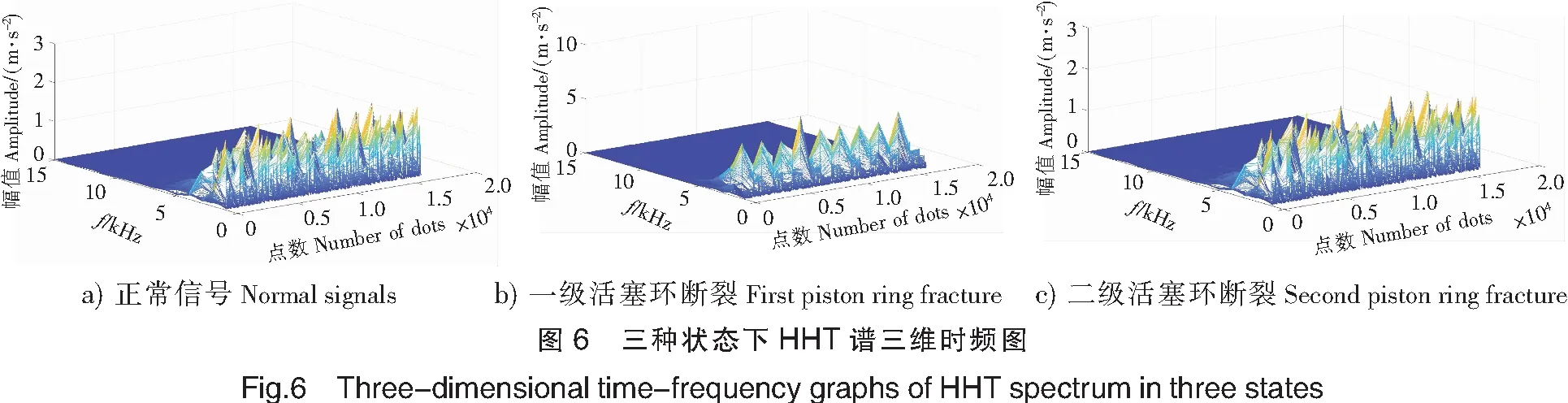
时频图所反映的频率能量分布，当空压机活塞环断裂时会激起船舶空压机系统的固有频率，此时形成共振，故幅值较大，能量较多，因此幅值较大的频段为固有频段(f)，且固有频段是0～5 000 Hz。不同的故障激起因有频段幅值不同，即能量不同，因此可以将空压机固有频段的能量值作为故障诊断的特征。由式(2)对希尔伯特谱进行时间(点数)积分便得到的希尔伯特边际谱，它能准确地反映信号幅值随频率变化的规律。

根据式(2)可以求出各个状态每个采集样本的0～5 000 Hz的希尔伯特边际谱能量值，即得到各种状态下固有频段的能量值。

4 马氏距离

马氏距离是多元数理统计理论中常用的判别方法之一，用于表示数据的协方差距离。该方法的计算是建立在总体样本的基础上，排除了变量之间相关性的干扰，是一种衡量两个未知样本集相似程度的有效方法[6]。由于算法简单，不受量纲的影响，计算速度快，并适用于小样本问题的处理，因此，被广泛应用于故障诊断领域。

使用HHT算法将采集到的振动信号进行分解，并得到希尔伯特边际谱，然后得到固有频段的能量值,以固有频段的能量值为特征值。选取每种状态下每个加速度传感器的5组共20组样本进行训练，其余20组进行测试。计算出每种状态下的20组样本的能量值的均值和方差，记为标准特征值Si和标准方差var(si)。三种状态下的标准特征值和标准方差如表2所示。

待检信号的固有频段能量特征值与三种状态下的标准特征值之间的马氏距离由式(3)计算得到。式(3)可以判断出两个样本之间的相似性，马氏距离越小，相似性越大。

(3)

其中：sx是待测样本数据的能量特征值；si和var(si)为标准特征值和标准方差；di是求得的马氏距离，d1表示正常状态，d2表示一级活塞断环，d3表示二级活塞断环。

表2 标准特征值及其标准方差

判断过程如下：取某一个测试样本的固有频段的能量值sx，然后分别代入三种状态下所对应的标准特征值和标准方差，求得三种状态下所对应的三个马氏距离(d1，d2，d3)，比较这三个马氏距离的大小，其中最小的数值所对应的状态为此样本所对应的状态(即：当d1最小时对应正常状态，当d2最小时对应的故障是一级活塞环断裂；当d3最小时对应的故障是二级活塞环断裂)，故而识别出该样本所对应的船用空压机的状态，达到故障诊断的目的。依照HHT边际谱和马氏距离判别方法的各个步骤，对三种不同状态下的空压机60组振动信号进行故障诊断研究，诊断结果表明：在正常状态下全部诊断正确，一级活塞断环有一处出现误判，二级活塞断环出现两处错误，故整体诊断正确率为95%。结果表明该方法可以进行船舶二级往复式空压机故障诊断，且诊断准确率较高。出现误判的原因可能是测量引起误差。部分诊断结果如表3所示。

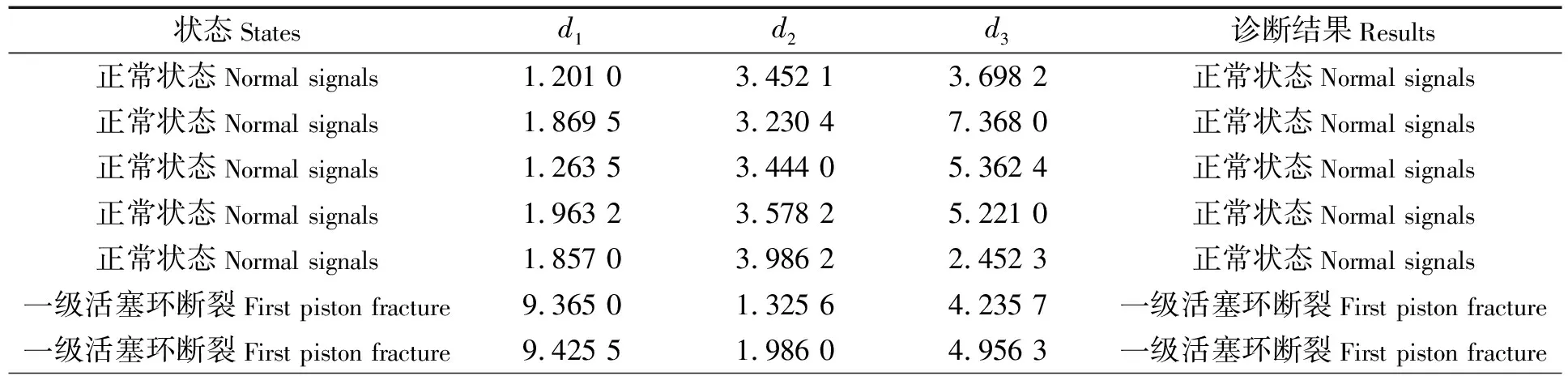
表3 部分马氏距离诊断结果

续表

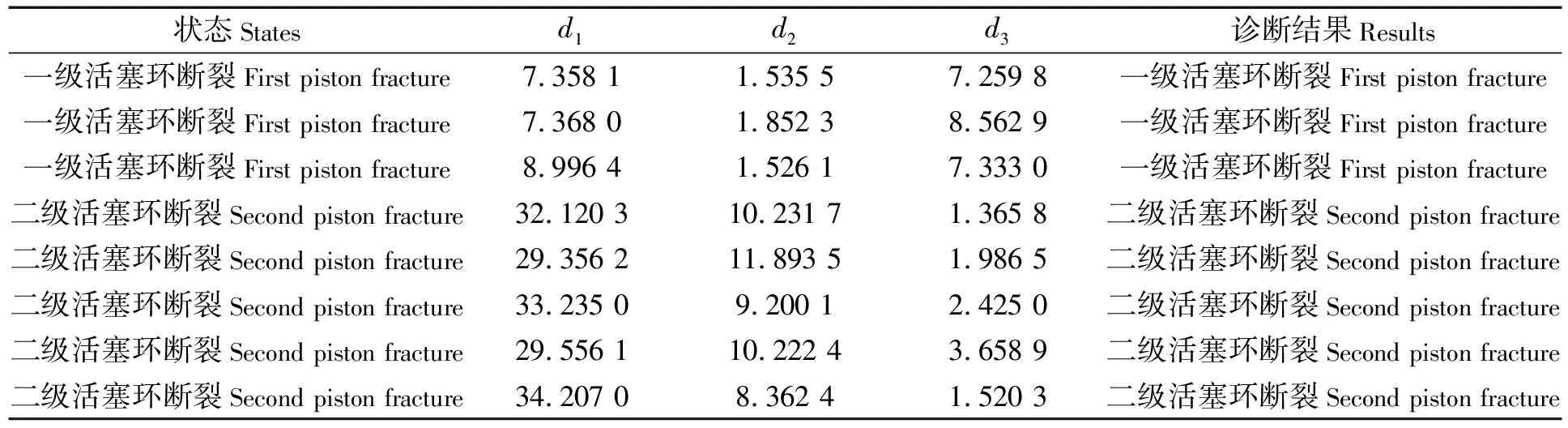
状态Statesd1d2d3诊断结果Results一级活塞环断裂First piston fracture7.358 11.535 57.259 8一级活塞环断裂First piston fracture一级活塞环断裂First piston fracture7.368 01.852 38.562 9一级活塞环断裂First piston fracture一级活塞环断裂First piston fracture8.996 41.526 17.333 0一级活塞环断裂First piston fracture二级活塞环断裂Second piston fracture32.120 3 10.231 71.365 8二级活塞环断裂Second piston fracture二级活塞环断裂Second piston fracture29.356 2 11.893 51.986 5二级活塞环断裂Second piston fracture二级活塞环断裂Second piston fracture33.235 09.200 12.425 0二级活塞环断裂Second piston fracture二级活塞环断裂Second piston fracture29.556 110.222 43.658 9二级活塞环断裂Second piston fracture二级活塞环断裂Second piston fracture34.207 08.362 41.520 3二级活塞环断裂Second piston fracture

5 结论

1)对于船舶二级往复式空压机振动信号的非线性非平稳性，采用EMD将其分解成若干个IMF分量，求出敏感IMF分量，进而对每个敏感IMF分量进行希尔伯特变换，再重构信号，得出希尔伯特边际谱，利用空压机固有频段的能量值作为信号的特征值，以此为判别马氏距离的依据。实验表明，该方法识别正确率在95%，可以有效进行故障识别。

2)一维离散小波降噪可以明显降低环境背景噪声干扰对振动信号的影响，提高了故障诊断的准确性。

3)在船舶往复式二级空压机断环故障诊断过程中，存在误判是因为存在测量误差和系统误差。本文的研究结果是基于小样本实验，要建立完善的空压机活塞环断裂的HHT边际谱的故障诊断还需要大数据进一步分析。