基于BP神经网络的织物表面绒毛质量的检测方法

2020-03-10金守峰林强强马秋瑞

纺织学报 2020年2期

金守峰，林强强，马秋瑞，张浩

(1. 西安工程大学机电工程学院，陕西西安 710048； 2. 西安工程大学服装与艺术设计学院，陕西西安 710048)

随着人们物质生活水平的提高，对织物表面的时尚性、舒适性等性能要求也在不断提升。为满足织物的外观、手感及保暖性的要求，在织物表面进行起毛工艺处理，使织物表面具有一定厚度，且分布一致的绒毛，该绒毛的状态影响着起毛后织物表面的性能和质量[1-2]。由于起毛工艺后织物表面绒毛的长度和形态较为复杂，现阶段对起毛织物的绒毛质量检测方法主要以有经验的工艺人员通过视觉和触觉的主观判断为准，检测人员的主观经验起主导作用，无法量化绒毛质量参数，检测绒毛织物是否合格的效率较低。

随着计算机技术和图像处理算法的不断提高，织物表面质量检测也向高效化和智能化方向发展，视觉测量技术已在织物质量检测领域得到了广泛应用。文献[3-5]针对织物疵点采用改进的函数滤波器、小波变换及形态学等方法进行识别与分类，这些方法结合改进的BP神经网络提升了织物疵点的细节特征精度，与传统的织物疵点检测方法相比，提高了识别效率[3-5]，但是，目前缺乏标准的织物疵点训练数据集，使得研究者应用的数据集各不相同[6-7]。文献[8-10]中针对织物在穿着过程中摩擦导致织物表面出现的起毛或起球等缺陷，采用傅里叶变换、小波变换等方法将起毛或起球织物图像变换至频域处理，并建立相应的织物起毛或起球的评价指标，通过机器视觉检测进行客观评价。文献[11]采用0.7～4.5倍的放大镜头获取织物表面绒毛的微观截面图像，建立了绒毛率检测的数学模型，实现了织物表面采样长度为 2～10 mm 内的表面绒毛率的测量。文献[11]与本文的研究内容相似，均是针对织物表面绒毛质量的检测，但与本文方法相比，文献所述方法由于采样长度较小，不能真实反映整幅织物表面的绒毛状态[11]。

为提高织物在起毛工艺后的绒毛质量检测效率，客观评价绒毛织物质量，实现自动化检测，本文提出基于BP神经网络织物表面绒毛质量的客观评定方法。该方法通过光切成像原理获取织物表面绒毛的轮廓图像，提取织物上边缘轮廓的特征点数据，以此为数据集训练构建的BP神经网络，并根据训练时间以及准确率对隐含层的神经元个数做相应的选择，最终以BP神经网络的输出值判别绒毛织物是否合格。

1 光切成像原理与自适应图像分割

1.1 光切成像原理

通过起毛工艺在织物表面形成具有一定厚度的致密绒毛，为获取织物表面绒毛厚度与分布状态信息，本文采用如图1所示的光切成像原理。

图1 光切成像原理Fig.1 Principle of light-cut imaging

相机与条形光源分别置于被测织物的两侧，条形光源为长方体形状，长×宽×高为37 cm×4.2×2.1 cm， LED(18&22PCS)光源，功率为5 W，4 500 K 自然光。条形光源置于辊子的正下方，使光线与辊子轴向轮廓边缘相切，采用背景光成像可避免受织物表面纹理及颜色特征的干扰，突出被测织物表面的绒毛边缘轮廓。织物包覆在辊子表面，随辊子匀速转动，当旋转至拍摄位置时，织物表面的绒毛在辊子的张力作用下其厚度及分布状态最为明显，此时相机获取到的织物图像如图2所示。

图2 绒毛织物切向图像Fig.2 Tangential image of fabric

在图2中，主要分为背景区域、绒毛区域以及绒毛底布区域。为获取更加清晰的织物图像，减少拍摄背景对织物绒毛轮廓的影响，采用黑色作为背景；绒毛区域经过条形光源照射后可清晰地与背景和底布区域分隔开，便于获取所需要的实验特征点数据集；绒毛底布区域则是未拉起绒毛的织物部分，是绒毛的基体。

1.2 自适应图像分割

将图像进行分割，将绒毛区域的特征提取出来，同时将背景区域和底布分开。由图3所示的灰度直方图分布特征可知，背景区域的灰度值集中分布在0～25之间，且像素个数远大于绒毛区域的像素数，而绒毛区域的灰度值集中在25～110之间，因此可利用最大类间方差法对图像进行自适应分割。提取的绒毛区域特征图如图4所示。

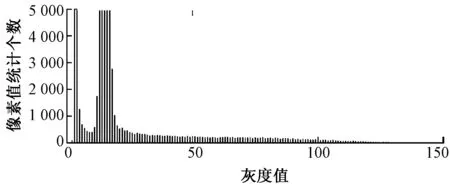
图3 灰度直方图Fig.3 Grayscale histogram

经过分割后的图像背景区域和绒毛底布区域与绒毛区域完全分离，图中白色区域为织物的绒毛部分，黑色为背景区域；且在图像中上边缘轮廓的起伏状态反映了该织物的绒毛厚度以及分布情况，应用Freeman链码原理对上边缘的轮廓特征进行提取，进而得到BP神经网络的训练数据集。

图4 绒毛区域Fig.4 Fabric binarization image

2 织物轮廓特征提取

链码技术最早用来作为线条的数据格式是由Freeman提出的，Freeman编码是目前一直在用的一种常用线条编码方式，链码的产生和定义都是按照边界曲线或曲线像素点用8邻接的方式进行，各个移动的方向按照数组{i|i=0,1,2,…,7}进行编码。各个方向都定义成与x轴正向的45°×i夹角。除8邻接的方式外，还有4邻接方式。

准确地提取织物边缘的轮廓特征是获得训练数据的前提和关键，本文通过应用Freeman链码编码方式的原理对织物绒毛边缘进行坐标点特征点的提取，其计算过程如下。

1)计算提取轮廓边缘的大小，记为M×N，而后生成(M+2,N+2)的0矩阵，将边缘轮廓嵌入其中，即用0将其包围，用来保证形成8邻域图像；

2)寻找第一个像素为1的坐标，即为第一个搜索方向的起点，而后对其余7个方向搜索，寻找下一个像素为1的坐标，依次进行搜索，并记录当前的坐标；

3)当其余7个方向均为0时，则停止计算，返回坐标值。通过应用上述算法，可提取织物绒毛轮廓的边缘坐标。将获得的绒毛织物轮廓边缘数据对应于原二值图像如图5所示，以该数据作为BP神经网络的训练数据集。由图可知，应用该方法提取的织物轮廓边缘坐标基本与织物上边缘吻合，可以反映边缘轮廓特征。

图5 织物绒毛轮廓边缘坐标提取Fig.5 Coordinate extraction of fabric fluff contour edge

3 绒毛质量检测的BP神经网络构建

BP神经网络是一种按误差反向传播算法进行网络训练的反馈型神经网络，3层BP神经网络模型如图6所示。将提取的织物轮廓坐标作为BP神经网络坐标数据集，并且对于合格的绒毛织物目标输出为1，其余不合格的目标输出为0，通过坐标数据集和目标输出对BP神经网络进行训练，实现绒毛织物是否合格的快速检测。

BP神经网络一般由3层组成，即输入层、隐含层(由1层或多层组成)和输出层。改变隐含层数量、神经元个数以及激活函数，可以实现非线性拟合[12-14]。如图6所示，xi为BP神经网络的输入，wmi为输入层与隐含层之间的连接权重，ki为隐含层各神经元的输出，wij为隐含层和输出层之间的连接权重，Yi为神经网络的输出值。输入层与权值wmi加权求和，然后作为输入与隐层激活函数做运算，得到的值再与权值wij求加权和，最后与输出层激活函数运算，得到整个BP神经网络的输出。

图6 3层BP神经网络Fig.6 Three-layer BP neural network

3.1 训练集制作

BP神经网络的学习属于有监督学习，需要1组已知目标输出的学习样本集。训练时先使用随机值作为权值，输入学习样本得到网络输出，然后根据输出值与目标输出计算误差，再由误差根据某种准则逐层修改权值，使误差减小，如此反复，直到误差不再下降，BP神经网络就训练完成。主要的训练阶段可分为工作信号的正向传播和误差信号的反向传播。

应用光切成像原理，共采集织物照片435张，其中合格绒毛织物225张，不合格绒毛织物210张，部分照片如图7所示。图7(a)示出生产检测合格的绒毛织物，数据集其标签为1，即BP神经网络期望输出值为1；图7(b)示出生产检测不合格的绒毛织物，数据集其标签为0，BP神经网络期望输出值为0，并应用Freeman链码提取原理对预处理后的织物边缘坐标进行提取，获得实际数据集大小为343×840的坐标矩阵。由于像素的横坐标是从1到840依次递增，为方便表示，在表1中省略了横坐标，仅表示了部分织物上边缘纵坐标数据。

图7 样本数据集部分照片Fig.7 Part of sample data set. (a)Production inspection of unqualified fabrics; (b)Production inspection qualified fabric

3.2 BP神经网络激活函数及学习函数

3.2.1 激活函数

激活函数给神经网络的神经元加入非线性因子，使得神经网络可以任意逼近任何非线性函数，从而使神经网络可以应用到众多的非线性关系模型中。BP神经网络一般使用Sigmoid函数和线性函数作为激活函数，而Sigmoid函数主要根据输出值是否包含负值又可分为Log-Sigmoid(见式(1))和Tan-Sigmoid函数(见式(2))[15-16]。

(1)

(2)

式中：x为输入值，其范围为整个实数域；e为自然常数，其值约为2.718 28；f(x)为函数输出。

Log-Sigmoid函数可以将输入从整个实数域的范围映射到(0，1)区间内，Tan-Sigmoid函数可以将输入从整个实数域的范围映射到(-1，1)区间内。并且Sigmoid函数可微，因而可以利用梯度下降法优化各权值，使权值更新以达到神经网络的学习。

3.2.2 训练函数

在权值更新过程中的训练算法主要为最速下降法，又称梯度下降法，是一种可微函数的优化算法，标准的最速下降法在实际应用过程中往往收敛速度比较慢，因此出现了动量BP算法、学习率可变的BP算法、拟牛顿法LM(levenberg-marquardt)算法[17-19]。

动量BP法是在标准的BP算法的权值更新基础上引入动量因子α(0<α<1)，使权值修正具有一定的惯性。

Δω(n)=-η(1-α)e(n)+αΔω(n-1)

(3)

式中：Δω(n)为第n次权值调整量；η为学习率；e(n) 为神经网络误差；Δω(n-1)为第n-1次权值调整量。因式αΔω(n-1)加入后，使本次权值的更新方向和幅度不仅与本次计算所得的梯度有关，并且还与上一次更新的梯度和幅度有关，使权值的更新具有一定的惯性，提高了抗震能力和加速收敛的能力[20]。

学习率可变的BP算法(VLBP)是通过误差的增减来判断的。当误差以减小的方式趋于目标时，说明修正方向是正确的，可以增加学习率；反之则减小学习率，并且撤销前一步修正过程，计算公式如下：

(4)

式中：η(n+1)和η(n)分别为第n+1次和n次学习率；kinc和kdec分别为增量和减量因子；e(n+1)和e(n)分别为第n+1次和第n次更新后神经网络总误差。

牛顿法是一种基于泰勒级数展开的快速优化算法，迭代公式如下：

ω(n+1)=ω(n)-H-1(n)g(n)

(5)

式中：ω(n+1)和ω(n)分别为第n+1次和第n次更新后神经网络权值；g(n)为第n次更新时的梯度；H为误差性能函数的Hessian矩阵。尽管牛顿法收敛速度快，但是需要计算误差性能函数的二阶导数，并且如果Hessian矩阵非正定，可能导致搜索方向不是函数下降方向，因此拟牛顿法应用一个不包含二阶导数的近似代替Hessian矩阵的逆矩阵，完成权值的更新。

LM算法类似拟牛顿，根据式(6)修正神经网络权值

ω(n+1)=ω(n)-[JTJ+μJ]-1JTe(n)

(6)

式中：J为包含误差性能函数对网络权值一阶导数的雅可比矩阵；μ为调节因子。

3.3 模型分析

根据以上网络参数，在实际网络的训练过程中，分别使用最速下降法、动量BP算法、学习率可变的BP算法、拟牛顿法、LM算法等权值更新的算法对神经网络进行训练，并且在隐含层分别使用Log-Sigmoid和Tan-Sigmoid 2种非线性函数为激活函数，在输出层分别使用Log-Sigmoid和Tan-Sigmoid 2种非线性函数以及线性函数(purelin)为激活函数对神经网络进行训练，结果如表1所示。traingd为批梯度下降训练函数，traingdm为动量批梯度下降函数，traingdx为动量及自适应梯度递减训练函数，trainb以权值或阈值为基准采用批处理的方式进行训练，trainscg为反向传播算法训练函数，trainr为随机顺序递增更新训练函数。

表1 神经网络模型分析Tab.1 Neural network model analysis

从表2中可以看出，训练的BP神经网络有 2组准确率达到了90%，考虑到实验的随机性，分别绘制出准确率在90%附近组合(共4组)的实际值和预测值，结果如图8所示，组合1学习函数为traingd，隐含层激活函数为tansig，输出层激活函数为tansig；组合2学习函数为traingdm，隐含层激活函数为logsig，输出层激活函数为purelin；组合3学习函数为traincsg，隐含层激活函数为logsig，输出层激活函数为tansig；组合4学习函数为trainr，隐含层激活函数为tansig，输出层激活函数为logsig。从中选取最优的BP神经网络组合。

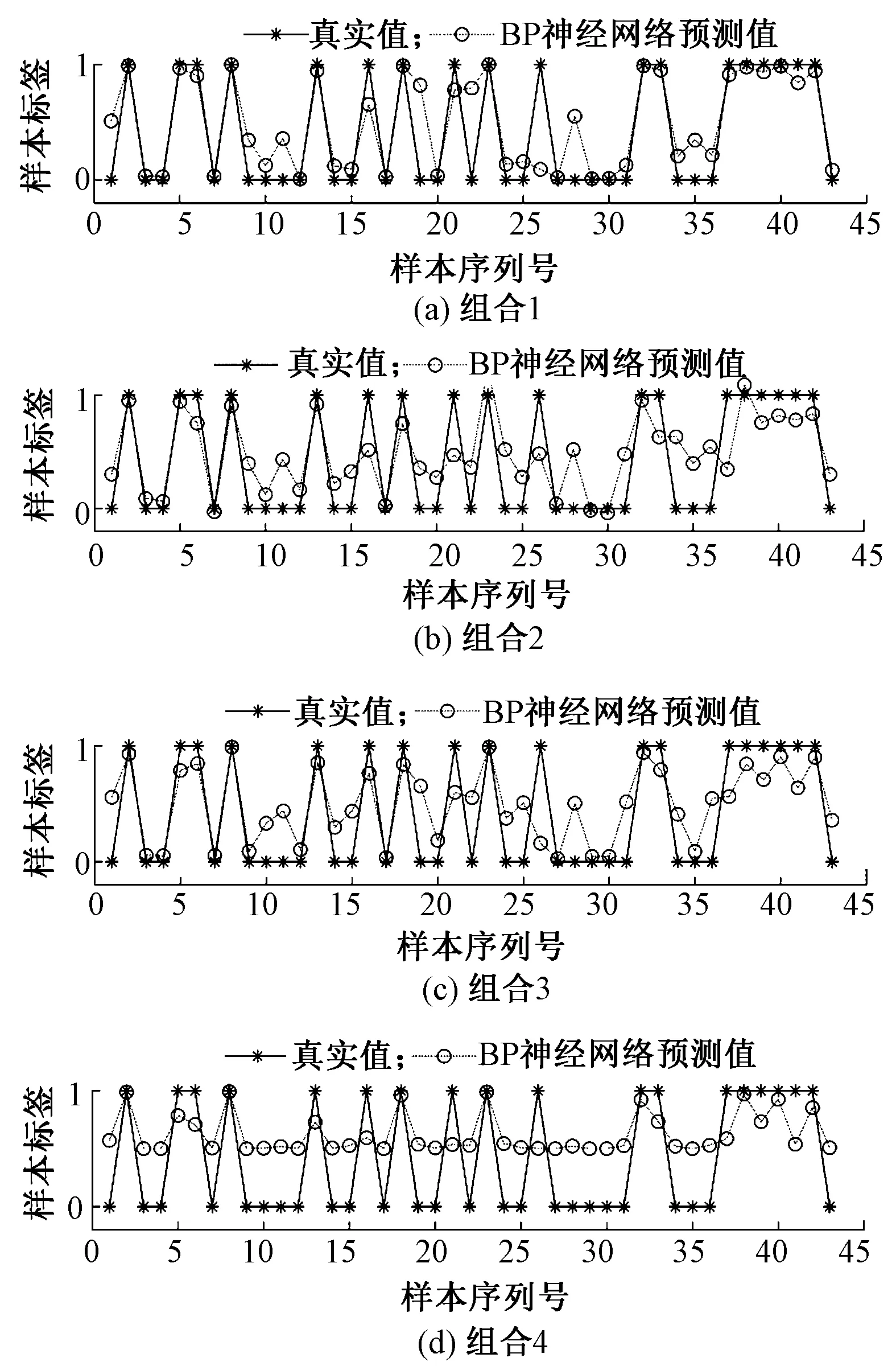
图8 不同组合的实际值和预测值Fig.8 Actual and predicted values for different combinations. (a)Combination 1; (b)Combination 2; (c)Combination 3; (d)Combination 4

由图8可知，在组合1中，当采用traingd的学习函数，隐含层应用tansig激活函数，输出层应用tansig激活函数时，神经网络的检测准确率为93.02%，并且预测点比较分散，与实际值最为接近。并且此时网络训练时间为11 s。构建的BP神经网络模型训练时间较短，经过训练后的神经网络模型检测准确率较高，在扩大数据集后可以满足实际的生产检测需求。

BP神经网络可以通过适当地增加隐含层神经元个数，从而实现任意的非线性关系映射。但随着隐含层神经元的个数增多，网络会变得复杂且训练时间会变长。目前BP神经网络隐含层神经元个数并没有明确的理论计算公式，只是依据如下3个经验公式获得：

(7)

m=log2n

(8)

(9)

式(7)～(9)中：m为隐含层神经元个数；n为输入层节点个数；l为输出层节点个数；α一般取1～10之间的常数。根据以上经验公式，分别计算得到隐层神经元个数为29、10、29。为得到最优的神经元个数，从5～40的范围内以间隔为5的标准，共选取8种不同的神经元个数作相应的训练，经过计算，当隐含层的神经元个数在10～20之间时，BP神经网络的预测准确率全部为93.02%，训练时间在 10 s 左右，网络比较稳定。

4 实验部分

本文实验以MatLab2018a为实验环境，应用其中的神经网络相关函数，完成所有的BP神经网络训练以及BP神经网络的测试。计算机处理器型号为：Intel(R) Core(TM) i5-4440 @3.10 GHz，安装内存为8 G。

为验证本文方法的精度和稳定性，对如图9所示的4种绒毛织物在运行速度为20 m/min，采样幅宽为700 mm的条件下进行多次测量。图9中(a)示出头道起毛工艺后的织物，织物表面生成的绒毛厚度不致密，且分布不均；图9(b)～(d)为不同颜色织物的末道起毛工艺后的表面状态，绒毛致密且分布均匀。

图9 起毛工艺后的织物Fig.9 Fabric after raising process. (a) First raising a#; (b) Final raising b#; (c) Final raising c#; (d) Final raising d#

由于BP神经网络输入的是织物的上边缘坐标，不需要织物的颜色和种类信息，在理论上适用于所有颜色的织物，由于实验条件有限，只采用了以上织物进行实验。织物类型a#为黑色经头道起毛工序生产的织物，b#、c#、d#为不同颜色的经末道起毛工序生产的织物；分别提取以上4种织物轮廓边缘特征，应用网络实际预测值和人工检测结果作对比，检测结果如表2所示。

由于构建的BP神经网络输入的训练数据是绒毛织的上边缘轮廓坐标，并没有输入颜色相关的信息，因此构建的BP神经网络对于颜色信息并不敏感。由表2可知，构建的BP神经网络对于不同颜

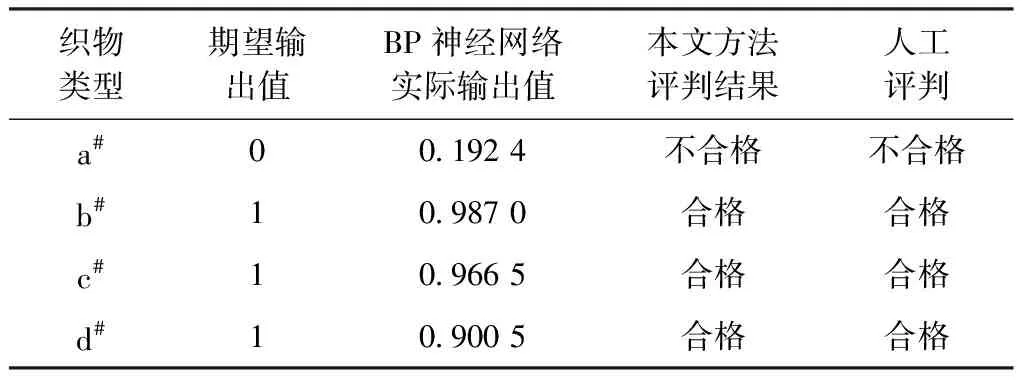
表2 检测结果对比Tab.2 Comparison of test results

色的绒毛织物都可完成检测，并且检测结果与人工评判保持一致。

经过训练后的BP神经网络得到2组权值，即为wmi和wij，经过加权求和，然后与激活函数运算后得到计算结果，即计算过程如式(10)所示：

F(x)=tansig(wij×tansig(wmi×x+b1)+b2)

(10)

经过训练后的BP神经网络权值如表3所示。其中wmi和wij分别为20×841和1×20大小的矩阵，b1和b2分别为20×1和1×1大小的矩阵。

表3 BP神经网络权值验证结果Tab.3 BP neural network weight verification results

由于构建的BP神经网络的输出值接近于0和1之间，因此设置0.5为阈值，即输出大于等于0.5的值全部设置为1，小于0.5的值则为0，计算结果与期望输出值对比如图10所示。

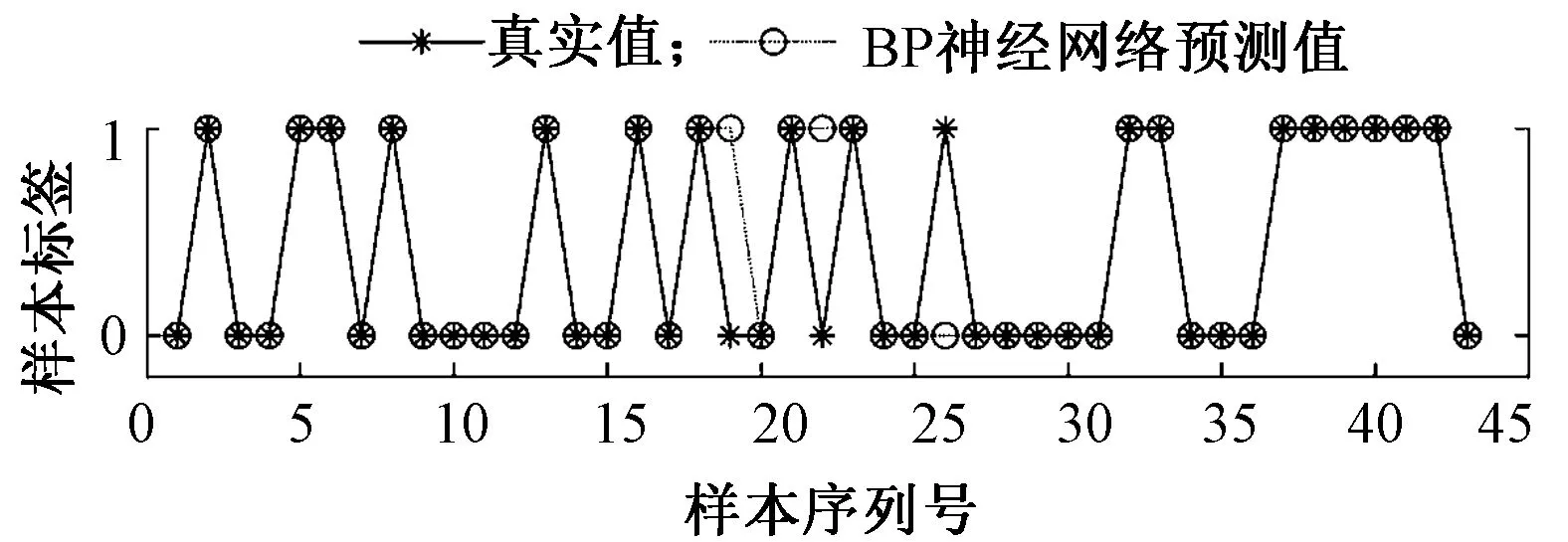
图10 计算权值验证Fig.10 Calculated weight verification

由图10可知，经过训练后的BP神经网络在输入所采集的绒毛织物轮廓的上边缘坐标数据后，经过BP神经网络的预测，对于生产合格的绒毛织物BP神经网络预测输出值为1，而对于生产不合格的绒毛织物BP神经网络预测输出值为0。应用权值与实际的输入坐标做矩阵运算，得到的预测结果也符合实际值，并且计算结果比较理想，因此，在实际计算过程中，可以应用网络训练后的权值采用式(10)与输入做相应的运算，得到检测结果，满足检测的时效性。