基于非对称极值Copula的设计暴雨过程线分析

2020-03-10陈子燊赵玲玲杨兴

人民珠江 2020年2期

陈子燊，赵玲玲,杨兴

(1. 中山大学新华学院,广东广州510520;2.中山大学地理科学与规划学院, 广东广州510275； 3. 广州地理研究所，广东广州510070;4.安徽理工大学地球与环境学院，安徽淮南232000)

台风灾害是全球发生频率最高的一种自然灾害。台风带来的极端降雨过程可导致山洪暴发和衍生滑坡等地质灾害，从而造成重大的生命财产和经济损失。如何应对极端暴雨是城市和山地防灾减灾都需面对的重大问题。一些研究人员从城市应对极端天气事件与防灾减灾的风险管理角度对雨型作了探索。蒋明[1]指出，雨型是描述降雨过程和降雨强度在时间尺度上的分配过程, 是径流过程计算的基础。成丹等[2]把设计雨型作为制定排水防涝系统设计时的重要因素，应用于城市市政排水系统的规划和管理及排水分析，为城市流域雨洪调度计算提供科学依据。叶姗姗等[3]选取宿迁市实测的主副型雨峰偏后的暴雨雨型，对其降雨过程进行同频率分时段缩放,采用Copula 函数的风险联合概率模型分析了不同的两时段之间出现的暴雨风险。杨星等[4]利用深圳雨量站34 a实测逐时降雨资料，对比了不同典型暴雨设计雨型研究方面的差异，按构建的两变量Copula推求了深圳市不同重现期雨型的风险率和典型暴雨的特征。

山区中小流域山洪至今仍然是防灾减灾的重要研究方向，为此，可借鉴设计洪水过程线的方法，从高维(大于二维)尺度上设计典型暴雨过程，将更有利于山洪风险管理。至今在应用Copula函数分析三变量洪水的联合概率分布和设计洪水过程线已有不少研究。侯芸芸等[5]和ZHANG等[6]分别应用对称的单参数Archimedean Copula函数分析了洪水三变量的联合概率分布和条件概率分布。由于具有不同相关性的高维随机变量，单参数难以真实反映其复杂的不对称相关结构。非对称形式的Copula 函数具有更加灵活的参数和结构形式，更适合用于拟合高维的随机变量[7 ]。为此，Grimaldi等[8]、Ganguli等[9]、陈子燊等[7]分别采用非对称的阿基米德Copulas(Asymmetric Archimedean Copulas)构建了不对称三变量洪水要素联合分布模型推算设计洪水，以尝试应用于洪水风险规划管理。肖义等[10]和李天元等[11]则分别采用两变量和三变量的Copula函数建立了联合分布的设计洪水过程线的推求方法，为设计洪水过程线提供了一种新思路。本文把非对称阿基米德极值Copula用于构建山区中小流域设计暴雨过程线，希望有助于防灾减灾的风险管理。

1 三变量Copula函数

1.1 Copula函数的定义

设随机变量Xi(i=1,2,…,n)的边缘分布函数分别为FXi(xi)=P(Xi≤xi)，其中n为随机变量的个数，xi为随机变量Xi的值。依Sklar理论，对于连续分布函数FXi(xi)，存在唯一的联合分布函数[6]：

H(x1,x2,…,xn)=C(FX1(x1),FX2(x2),…,FXn(xn))=C(u1,u2,…,un)

(1)

利用Copula函数构造联合概率分布，使得变量的所有信息都存在于边缘分布函数里，不会在转换过程中产生信息失真。因此，Copula函数理论是构建多变量水文联合概率分布的很好的工具[12]。

1.2 三变量Archimedean Copula

三变量对称的Archimedean Copula单参数形式[13]为：

(2)

式中uj∈[0,1](j>1)——边缘分布;φθ——Archimedean Copula生成元，θ——参数。

φθ(u3)]

(3)

三变量非对称Archimedean Copula的形式为[14]：

C(u1,u2,u3)=C1(u3,C2(u1,u2))=

(4)

式中符号“0”——函数组合。

常用的三维非对称Archimedean族Copula函数如下。

a) M3 (Frank) Copula

(1-e-θ1u3))},θ2>θ1∈[0,∞)

(5)

b) M4 (Clayton) Copula

(6)

c) M5 (Arch2) Copula

(7)

d) M6(Gumbel-Hougaard) Copula

C(u1,u2,u3)=exp{-([(-lnu1)θ2+(-lnu2)θ2]θ1/θ2+(-lnu3)θ1)1/θ1},θ2>θ1∈[1,∞)

(8)

e) M12 (Arch12) Copula

(9)

1.3 三变量联合重现期和条件重现期

以算符“∨”定义“或”三维极端事件中至少有一个被超过情况下的“或”联合重现期为：

(10)

以“∧”定义“且”三维极端事件同时被超过情况下的“且”联合重现期为:

(11)

2个不超过事件发生下的条件概率为[5]：

(12)

则事件(X1>x1|X2≤x2,X3≤x3)下的条件重现期为:

T(x1|X2≤x2,X3≤x3)=

(13)

2个等量事件发生下的条件概率为：

F(x1|X2=x2,X3=x3)=

(14)

则事件(X1>x1|X2=x2,X3=x3)下的条件重现期为:

T(x1|X2=x2,X3=x3)=

(15)

一个等量事件发生下的条件概率为:

(16)

则事件至少有一个为超过事件下的条件重现期为:

(17)

一个不超过事件发生下的条件概率为:

(18)

则事件至少有一个为超过事件下的条件重现期为:

(19)

2 实例研究

2.1 流域水文气象背景与基本数据

选取广东曹江流域为实例研究。曹江是广东独流入海鉴江的一级支流，发源于高州马贵镇山心村的蓝蓬岭。出口断面大拜水文站集水面积394 km2，属于典型的中小流域。曹江流域多年平均年雨量约2 160 mm，最大年雨量可达3 150 mm，是广东的台风暴雨高区之一。1967年11月7日代号为6720 的“Emma”超强台风，在流域西侧的湛江市登陆，最大风速65 m/s，中心气压912 hPa。2013年8月14日代号为“Utor”的超强台风，在流域东侧的阳江市登陆，最大风速60 m/s，中心气压925 hPa。大拜雨量站测得二者最大24 h暴雨分别为419.9、412.1 mm，均达到特大暴雨级别，也是1967—2013年2个最大的24 h小时雨量。

本文根据曹江流域出口断面大拜雨量站1967—2013年逐时降水记录数据，首先提取历年最大24 h雨量(R24)，再分别提取最大1 h雨量(雨峰：R1)和连续最大6 h雨量(R6)数据，由R1、R6和R24作为实例分析的样本，分别构建1967、2013年这3个历时雨量联合分布的2场设计暴雨过程线。

2.2 边缘分布与联合分布

分别采用皮尔逊三型分布(PE3)和广义极值分布(GEV)对R1、R6和R24样本加以拟合。参数估计使用线性矩(L-矩)方法。经验频率分布使用Gringorten公式计算。拟合结果采用均方根误差(RMSE)和概率点据相关系数(PPCC)检验其拟合优度。表1择优对比结果表明，R1、R6和R24都以GEV分布相对更优。广义极值(GEV)分布函数为：

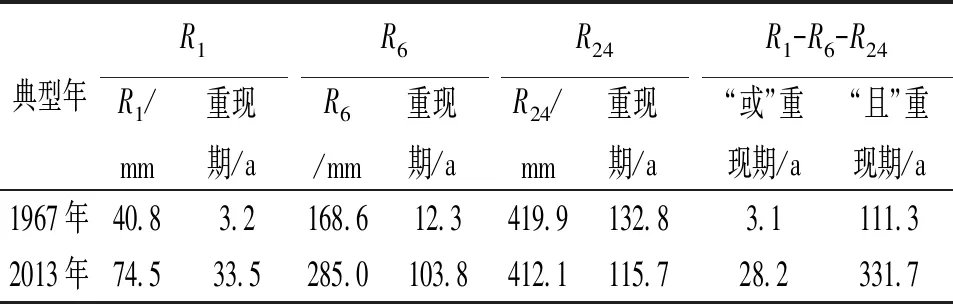
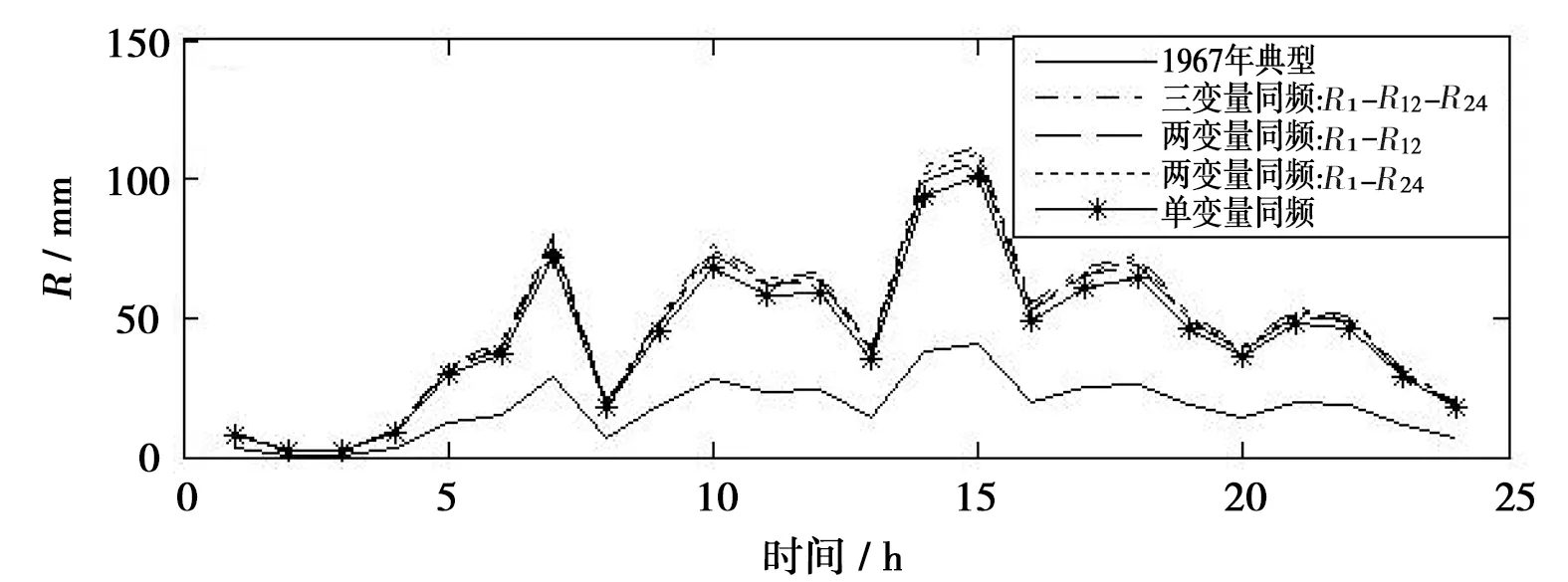
FX(x)=P(X

(20)

式中ξ、β、μ——形态参数、尺度参数和位置参数。

表1 曹江大拜站三变量暴雨样本的边缘分布参数与优度检验值

计算的R1、R6和R24两两间的Kendall 相关系数表明大拜雨量站不同历时暴雨间都存在正相关性，其中R6和R24最强，τ= 0. 484;R1和R6相关性次之，τ=0.399;R1和R24相关性较弱，τ= 0.171。采用Kendall相关系数τ与Copula参数θ的关系式，构建5种非对称Archimedean Copula[6]。为了对比，分别将对应的5种对称三变量Archimedean Copula通过MLM法计算其参数θ。采用Akaike 信息准则(AIC)、最小(OLS)准则和Genest-Rivest图形法验证理论联合分布函数与经验联合分布函数的拟合程度，结果见表2和图1。可见以二维Gumbel-Hougaard 为基Copula的三维非对称形式的M6 Copula 的OLS和AIC值最小，拟合度最高，各点均匀地分布在45°线左右的非对称Archimedean M6 Copula具有相对最优的拟合度。Nelson[13]和Salvadori等[14]证明当且仅当边缘分布和Copula函数均为极值分布时，构造的联合分布才是极值分布，而Gumbel-Hougaard Copula是Archimedean Copula函数族中的唯一多变量极值Copula函数，适用于极端事件的频率分析。考虑到R1、R6和R24之间的相关性存在明显差别，因此，选用非对称Archimedean M6 Copula构建大拜雨量站历年最大24 h暴雨量不同历时R1、R6和R24之间的三维联合分布:

C(u1,u2,u3)=exp{-([(-lnu1)1.937+

(-lnu2)1.937]1.395/1.937+(-lnu3)1.395)1/1.395}

(21)

表2 非对称和对称三维Copula 参数估计及拟合优度对比评价

a) M2 b) M4 c) M5 d) M6 e)M12图1 5种非对称Archimedean Copula的概率分布拟合

2.3 典型暴雨过程线选择

典型暴雨的特征，包括降雨集中程度、雨峰位置和雨峰大小等。典型暴雨过程线的选择采用以下原则: ①选择雨峰量大具有一定代表性的实测暴雨过程线；②从防洪安全考虑，对主峰靠后和主峰靠前的2种雨型的风险概率加以对比;③设计暴雨过程线采用同频率放大法，以降水主峰对流域洪水形成为首要影响因子，选定时段为1 h的设计雨峰为设计标准，使得放大的过程线形状能与原来的典型过程一致。

按照短历时强降水强度20 mm/h划分雨峰，根据典型年暴雨过程的雨峰位置，选取1967、2013年作为曹江流域设计暴雨的典型年,24 h暴雨过程线见图2。图2显示，1967年最大24 h暴雨过程为主副多峰雨型，主峰靠后，2013年最大24 h暴雨过程为单峰雨型，主峰靠前。这2个典型暴雨R1、R6、R243个时段最大降水量与相应的重现期见表3。

a) 1967年

b) 2013年图2 2个典型年的最大24 h暴雨过程

表3 2个典型年R1、R6、R24最大降水量及重现期

典型年R1R1/mm重现期/aR6R6/mm重现期/aR24R24/mm重现期/aR1-R6-R24“或”重现期/a“且”重现期/a1967年40.83.2168.612.3419.9132.83.1111.32013年74.533.5285.0103.8412.1115.728.2331.7

从表3可见，1967、2013年的R1-R6-R24组合雨量的“或”联合重现期小于单一时段雨量重现期，此说明考虑多时段组合条件下某一时段雨量致灾的可能性最高，相比较同时出现三时段组合雨量的“且”联合重现期可能性很小。表4为不同时段雨量组合的“或”联合重现期，可见同频率下R1-R6-R24三时段组合雨量的“或”联合重现期最小，危险率最高。因此，如果以三时段雨量组合的“或”联合重现期作为流域的防雨洪标准，由此设计的暴雨过程线对于应对流域雨洪风险更合适。

表4 不同时段雨量组合的“或”联合重现期

2.4 同频率法推求设计暴雨过程线

有关研究指出[11]，由于对任一给定的三变量重现期Tu1,u2,u3，理论上存在无数种u1、u2、u3的组合满足式(10)，如果按照同频率放大法的思路，假定R1、R6、R243个时段雨量同频率，即令u1=u2=u3，可得到基于某一联合重现期Tu1,u2,u3的频率组合(u1,u2,u3)。根据此组合，按照各变量的边缘分布函数反推可得到3个不同时段雨量的联合设计值组合(r1、r6、r24)，进而以此设计值组合放大典型暴雨过程，即得到基于三变量联合分布的设计暴雨过程线。采用非对称M6函数推算R1、R6、R243个时段雨量同频率分布联合设计值公式如下：

u1=u2=u3=[1-(1/Tu1,u2,u3)]α;

(22)

按相同原理，可分别推算两变量u1、u2的重现期Tu1、u2，u1、u3的重现期Tu1、u3和u2、u3的重现期Tu2,u3的同频率分布联合设计值。

从表5多变量同频率设计值计算结果可见，R1-R6-R24组合同频率设计暴雨设计值明显大于其它同一重现水平组合和单一时段暴雨的设计值。由于多变量方法是基于多个时段组合的联合重现期，考虑了变量之间的相关性，设计值会大于单变量同频率设计值。有关研究结果显示[7,15]，三变量同频率设计值十分接近于按联合概率密度最大值推算的三变量“或”重现期设计值。作为工程设计与风险管理，尽管存在偏向安全问题，但采用R1-R6-R24组合同频率设计暴雨值为更高安全标准的防雨洪工程设计或风险预警提供了科学依据。

表5 样本设计值

选取1967、2013年的受台风影响的2场典型暴雨过程进行同频率分时段缩放。放大系数公式:

K=X设计/X典型

(23)

式中X设计——不同重现期的设计降雨量；X典型——典型暴雨降雨量。

以雨峰同频率放大法求重现期200 a(P=0.05%)R1-R6-R24三时段雨量联合分布的设计暴雨过程线。为了比较，另推求了R1-R6和R1-R24两变量联合分布以及以雨峰同频率放大的设计暴雨过程线。由图3可见，多变量方法与单变量方法所推求的200年一遇设计暴雨过程线的比较显示，采用R1-R6-R24组合方法推求的3个时段雨量的设计值均大于相应单一时段样本推算的设计值，也大于采用2个时段雨量组合的设计值。可见，采用R1-R6-R24组合方法放大的过程线对流域防雨洪设计工程更安全，采用R1-R6-R24组合的设计暴雨过程线也更加符合流域水文现象的内在规律和防洪工程实际的要求。

a) 1967年

b) 2013年图3 200年一遇设计暴雨过程线比较

2.5 设计暴雨过程线的条件重现期及危险率

按式(12)—(19)分别推算了1967、2013年典型暴雨过程的条件重现期及相应的条件概率，结果见表6。结果显示：①等量事件发生条件下的条件重现期小于不超过事件发生下的条件重现期，出现的危险率P(超值条件概率)则大之；②1967年典型暴雨出现的4个条件重现期都分别小于2013年主峰靠前的单峰雨型的对应条件重现期，危险率则反之。其中，等于24 h雨量(419.9 mm) 一个等量事件条件下出现的重现期最小，危险率最大。这表明主副多峰雨型且主峰靠后1967年暴雨过程对于流域防洪安全具有更大的威胁。