地面堆载诱发下既有盾构隧道纵向变形的解析解

张 勇， 马金荣， 陶祥令, 2, 李 阳

(1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室， 江苏 徐州 221116； 2. 江苏建筑职业技术学院能源与交通工程学院， 江苏 徐州 221116; 3. 中国建筑股份有限公司, 北京 100029)

0 引言

随着社会经济的持续发展，城市地下轨道交通网络不断完善，紧邻既有地铁线路的建筑施工越来越多，由此引发的地面堆载对既有隧道的影响问题日益突出。根据相关统计，仅2014年上海地区地铁沿线地面突发堆载达到16次[1]。地面堆载[2]将引起下部土体沉降，使得隧道结构产生较大变形，严重时将造成螺栓断裂、管片局部开裂等病害，对地铁隧道运营安全危害极大。

目前地面堆载对临近盾构隧道影响的研究方法主要有现场监测[3-5]、理论解析[6-8]、数值模拟[9-10]、室内模型试验[11-12]等。其中理论解析法概念明确，计算简便，因而得到广泛应用。在理论计算研究方面，主要有2种思路： 一种是将隧道视为置于地基模型上的连续梁，如李春良等[6]考虑了接头对隧道抗弯刚度的影响，建立盾构管片的纵向梁模型，并分析了影响隧道力学行为的各种因素； 戴宏伟等[7]基于文克尔地基梁模型，研究了施工荷载对临近隧道的影响； 璩继立等[13]把隧道等效为双面弹性地基梁，运用有限差分原理解出隧道的纵向变形和内力，并对比Winkler地基梁模型计算结果； 康成等[14]将盾构隧道简化为置于Winkler地基上的Timoshenko梁，并计算了盾构隧道的纵向变形及内力。另一种是将盾构隧道视为完全离散的弹性地基短梁，如魏纲等[15]基于剪切错台模型，解得隧道纵向位移以及相邻管片环之间的错台量； 魏新江等[16]建立同时考虑管片剪切错台和刚体转动的隧道变形模式，运用最小势能原理推导出盾构隧道纵向变形以及内力计算公式。第1种研究思路隧道结构变形原理明确，概念清晰，易于理解，因而得到广泛应用； 而第2种研究思路虽然更能反映盾构隧道实际变形模式，但由于基于能量法，概念较复杂，计算繁琐，且环间剪切刚度等参数的确定存在问题，因此相关应用还不多。本文延续第1种研究思路，将隧道视作置于地基模型上的连续梁，导出变形微分方程进行求解。

不难发现，现有计算方法基本是将盾构隧道简化为置于Winkler地基上的Euler-Bernoulli梁。Euler-Bernoulli梁忽略梁的剪切变形[17]，但实际工程中，盾构隧道是由管片与螺栓组成的复合结构物，盾构隧道不仅发生弯曲变形，而且还发生剪切错台变形[18]。因此，Euler-Bernoulli梁的适用性受到极大限制。康成等[14]虽然考虑了隧道的剪切效应，却仍采用传统的Winkler模型作为地基模型，Winkler模型仅含1个参数，尽管运算简便，但忽视地基连续性，不能反映实际变形情况[19]。

针对以上不足，本文基于现有研究，考虑连接螺栓的存在对隧道整体剪切刚度的减弱[14]，以及地基变形的连续性，把盾构隧道简化为置于Pasternak地基模型上的Timoshenko梁(本文中定义为T-P模型)。Timoshenko 梁具有2个广义位移，能够真实反映梁在剪切作用下的变形特性[20]； 同时，Pasternak地基克服了Winkler模型的缺陷，通过加入剪切刚度为Gs的剪切层，考虑传统地基弹簧之间的相互作用[19]，能够反映地基连续性。相比之前常用的计算模型，本文T-P模型更符合盾构隧道实际受力、变形情况。

根据上述模型导出地面堆载作用下临近盾构隧道竖向变形的微分控制方程，运用有限差分原理解得其数值解。之后，对比分析理论计算结果与实际监测数据，以验证模型的适用性。最后，通过参数分析研究隧道变形对于各影响因素的敏感性。

1 隧道纵向变形计算模型建立

1.1 地表堆载引起既有隧道附加荷载计算

1.1.1 建立地面堆载力学模型

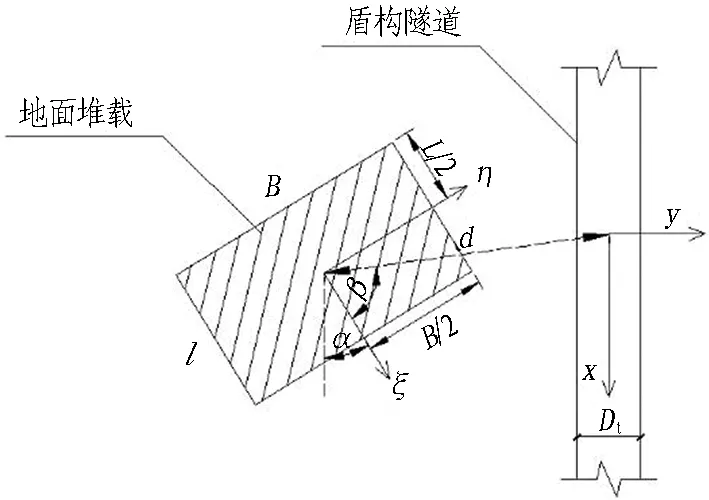
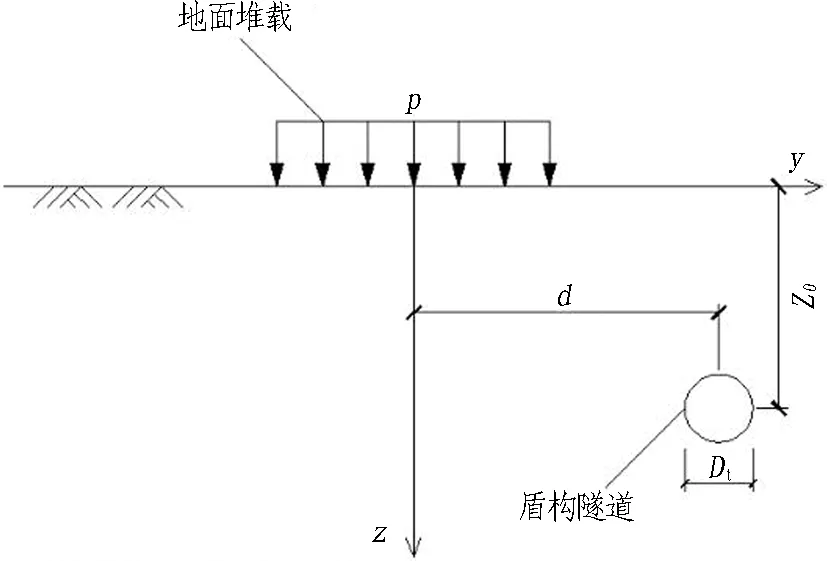
图1示出地面堆载与既有盾构隧道位置关系。

1.1.2 采用Boussinesq解计算附加应力

依据Boussinesq公式，积分可得地面堆载作用下隧道轴线上某点的附加应力：

(1)

式中：Ω为地面堆载积分区域；p为堆载的大小；R为控制隧道与荷载相对位置的参数

(2)

式中(ξ,η)和(X,Y,z0)分别为地面堆载范围内一点、隧道轴线上某点在全局坐标系ξ-η下的坐标。

为简化计算，建立局部坐标系x-y，坐标原点为隧道轴线上一点，x轴与隧道轴线重合，y轴垂直于隧道轴线； 全局坐标系与局部坐标系原点水平距离为d，ξ轴与x轴夹角为α，ξ轴与两坐标系原点连线夹角为β。则由几何关系，可得两坐标系之间的转换关系为：

X=ysinα+xcosα+dcosβ；

(3)

Y=ycosα-xsinα+dsinβ。

(4)

(a) 平面图

(b) 截面图

1.2 基于T-P模型的既有盾构隧道纵向变形推导

本文假定盾构隧道为置于Pasternak地基模型上的Timoshenko 梁(T-P模型)，计算模型如图2所示。

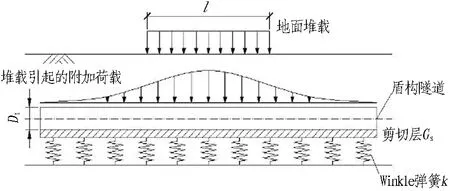
图2 计算模型

根据Timoshenko梁理论，可得梁弯矩ML和剪力QL：

(5)

(6)

式中： (κGA)eq为隧道等效剪切刚度； (EI)eq为隧道等效抗弯刚度；θ为梁截面转角。

在竖向分布荷载q(x)作用下，基于本文模型，根据微元体竖向受力平衡方程和弯矩平衡方程，可得盾构隧道竖向变形w(x)的微分控制方程：

(7)

同时，还可以得到隧道剪力Q和弯矩M的微分控制方程：

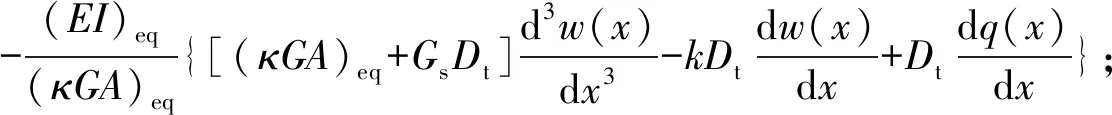
(8)

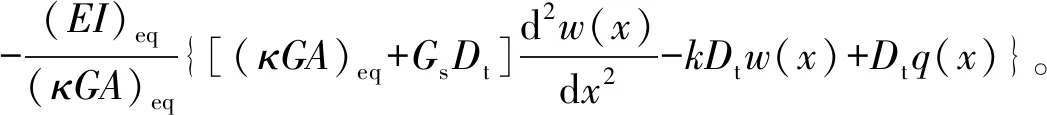
(9)

求解式(7)即可得到在地面堆载p引起的附加荷载q(x)作用下既有盾构隧道的纵向变形，运用有限差分原理求其数值解。

将隧道分成n段，每段长为l′，隧道两端分别有2个虚节点，这样隧道离散为n+5个节点单元，如图3所示。

图3 有限差分网格

基于有限差分原理，即可得微分方程式(7)的有限差分形式：

(10)

假定隧道两端自由，则有边界条件： 隧道两端的弯矩M及剪力Q为0。结合边界条件，式(10)即可写成以隧道竖向变形w为未知数的矩阵-向量表达式：

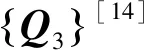
(11)

式中： {[K1]-[K2]+[K3]}为常系数刚度矩阵； {w}为隧道的竖向变形列向量； {Q1}为附加荷载列向量； {Q2}为附加荷载修正列向量； {Q3}为补充列向量。

在已知地面堆载的情况下，即可求得盾构隧道的纵向变形，进一步还可求得盾构隧道内力(弯矩和剪力)及变形(管片错台量和接头张开量)的纵向分布。

2 相关计算参数确定

2.1 隧道等效抗弯刚度

目前，广泛采用Shiba等[21]建立的竖向等效连续化模型，其等效抗弯刚度(EI)eq表达式为：

(12)

式中：Ec为管片弹性模量；Ic为隧道截面惯性矩；ψ为隧道断面中性轴位置，ψ的计算表达式为：

(13)

式中：kb为接头螺栓的平均线刚度(kb=EbAb/lb; 其中Eb为螺栓弹性模量；Ab为螺栓的横截面积；lb为螺栓长度)；ls为环宽；Ac为隧道管片截面积；n为螺栓个数。

管片接头张开量O与弯矩M有关，根据几何关系，计算公式可以表示为：

(14)

2.2 隧道等效剪切刚度

WU H. N.等[18]给出盾构隧道等效剪切刚度(κGA)eq的计算公式为：

(15)

式中：ζ为修正系数；κb和κc分别为螺栓及管片环Timoshenko剪切系数，分别取0.9、0.5；Gb和Gc分别为螺栓和管片的剪切刚度：

(16)

(17)

式(16)—(17)中νb和νc分别为螺栓及管片的泊松比。

根据几何关系，WU H. N.等[18]进一步推导出了管片错台量C的计算公式：

(18)

2.3 Pasternak地基相关参数

Pasternak地基模型[19]在传统Winkler 模型基础上增加1个剪切刚度为Gs的剪切层，能够考虑地基弹簧的相互作用。Pasternak地基模型基床反力可表示为：

(19)

式中：p′为Pasternak模型基床反力；k为基床反力系数；w(x)为地基变形量；Gs为地基剪切刚度。

Tanahashi[23]建议采用以下经验公式来估算Pasternak地基剪切刚度：

(20)

式中：Es为土的弹性模量；ν为土的泊松比；ht为Pasternak模型中变形影响深度，徐凌[24]经过研究指出，在分析土-隧道相互作用时，ht取2.5倍隧道直径Dt。

Vesic[25]建议置于地表上的长梁地基反力系数表达式为：

(21)

Attewell等[26]建议采用2倍kVesic数值，大致估算出具有一定埋置深度地基梁的基床反力系数，即：

k=2kVesic。

(22)

本文采用Attewell等[26]的建议，利用式(22)计算Pasternak地基的基床系数。

3 实例验证

3.1 工程概况

小涞港河道位于上海地铁9号线某区间盾构段正上方，两者位置关系及相关参数如图4所示。由于附近工程施工，河道内回填土方[27]。回填土的高度为4.5 m，回填土重度γ=17 kN/m3，回填土重力荷载将导致下方盾构隧道产生不均匀沉降。计算中考虑河道水位降低1 m的影响。隧道断面所在土层性质如表1所示，上海地区盾构隧道管片结构参数如表2所示。

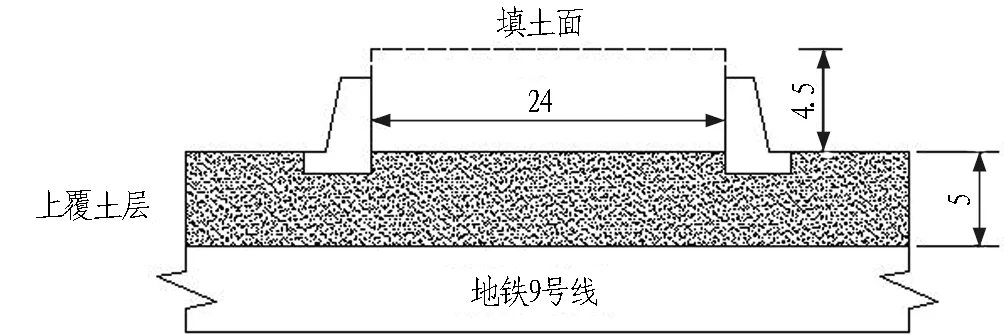
图4 河道与隧道相对位置关系(单位： m)

表1 土层物理力学参数

表2 隧道管片结构参数[17]

3.2 计算结果分析

图5示出几种理论模型计算结果与实测数据的对比。由图5可知： 4种理论模型计算结果相近，在河道堆载作用下，盾构隧道竖向变形呈正态分布，隧道中心处竖向变形最大，向两边逐渐减少。隧道竖向变形主要发生在河道加载中心两侧40 m范围内，为3～4倍的加载宽度，这与文献[27]的研究结论相符。采用本文提出的T-P模型，隧道最大竖向变形为27.6 mm； EB-W模型(置于Winkler地基上的Euler-Bernoulli梁)计算结果稍小，为26.7 mm； EB-P模型(置于Winkler地基上的Pasternak梁)计算结果最小，为26mm； 康成等[14]采用的T-W模型计算结果最大，为28.4 mm。究其原因，本文提出的模型基于Timoshenko梁单元，能够考虑盾构管片螺栓接头对隧道整体剪切刚度的削弱，因此计算结果相比常用的Euler-Bernoulli梁模型较大。此外，本文T-P模型考虑了传统地基弹簧之间的相互作用，能够反映地基变形连续性，因此计算结果稍小于T-W模型。根据T-P模型和EB-W模型得到的隧道最大竖向变形均大于EB-P模型，但前者数值更大，表明理论模型采用Timoshenko梁单元相比Pasternak地基，对盾构隧道竖向变形性能影响更大。

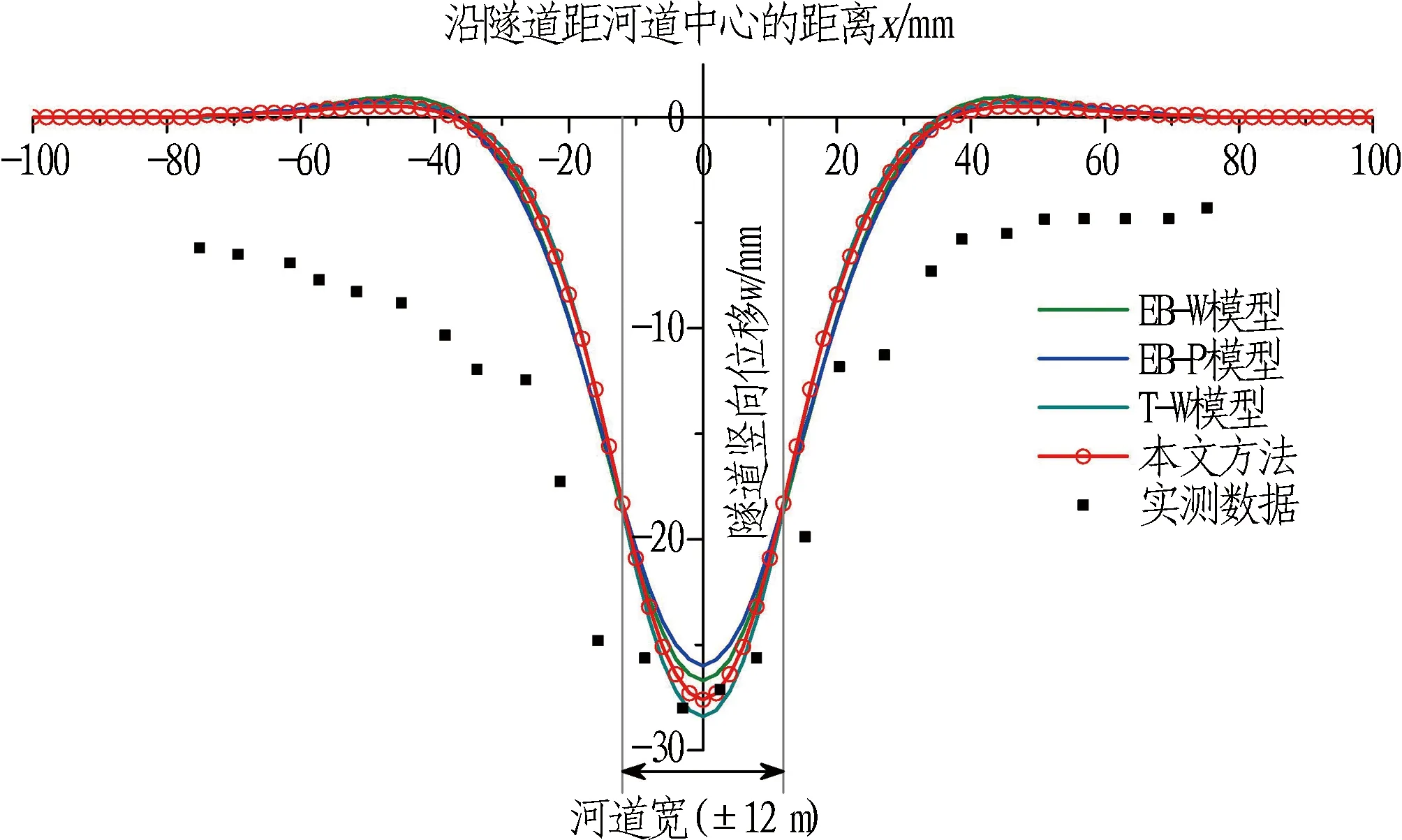
图5 理论计算结果与实测数据对比

从图5中还可以发现，在河道加载中心两侧20 m范围内，几种理论模型所得隧道竖向变形分布与监测数据均大致吻合，但在实测数据的最大值附近，本文理论模型计算结果相比其他模型更接近实测值。本文模型相比其他几种常用的计算模型，还可以进一步得到盾构隧道管片错台量，从而更准确地描述盾构隧道的复合结构形式。此外，在距加载中心20 m范围外，实测变形比包括本文方法在内的几种模型计算结果都大得多，分析原因，在实际工程中，距离地面堆载较远的盾构隧道会受到堆载之外的其他因素的影响，也会产生一定的变形量。

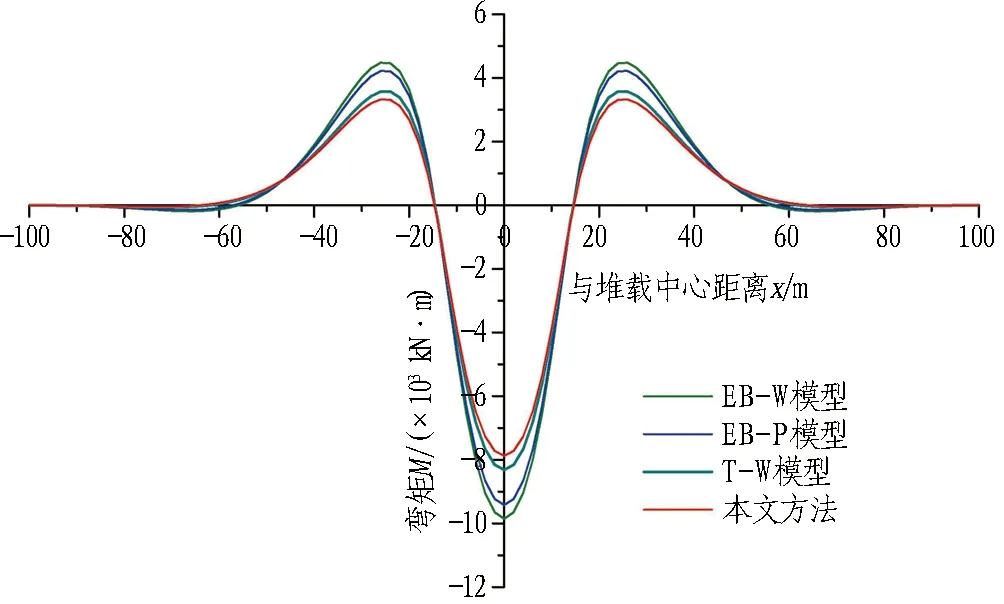
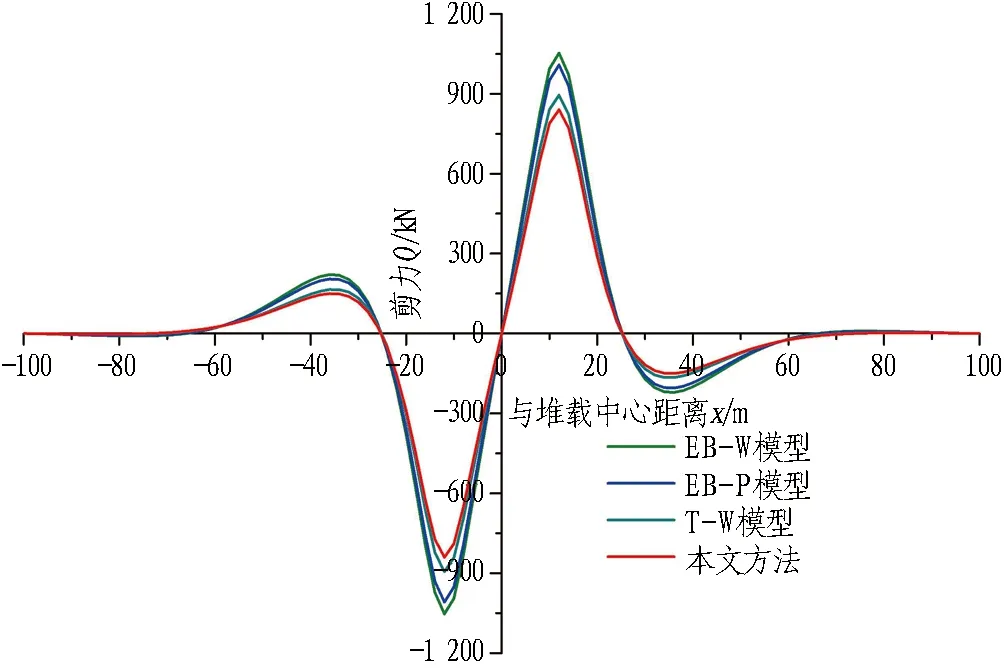
图6给出了采用几种理论模型计算得到的隧道纵向弯矩、剪力、接头张开量及管片错台量对比图。由图6可知： 基于Euler-Bernoulli梁的2种模型计算结果相近，而本文T-P模型与康成等[14]采用的T-W模型计算结果更为相近。Euler-Bernoulli梁由于不能考虑管片螺栓接头的存在而导致的隧道整体刚度的削减，内力计算结果较大； 常规EB-W模型计算所得弯矩、剪力最大值为本文T-P模型的1.3倍，亦为T-W模型的1.2倍。对比EB-W和EB-P模型计算结果，以及T-W和T-P模型计算结果，Pasternak地基模型因剪切层的存在，能够考虑地基连续性，因此基于Pasternak地基的模型相比基于传统Winkler地基的模型，计算得到的隧道纵向内力较小。

此外，通过分析图6(a)和图6(b)还可以发现： 隧道最大正弯矩(下侧受拉为正)位于堆载中心，而隧道最大负弯矩位于堆载中心两侧1倍加载宽度(±24 m)处，最大正弯矩约为最大负弯矩的2.3倍； 隧道最大剪力出现在堆载边界(±12 m)处。这几个截面均较危险，实际工程中应给予足够重视。

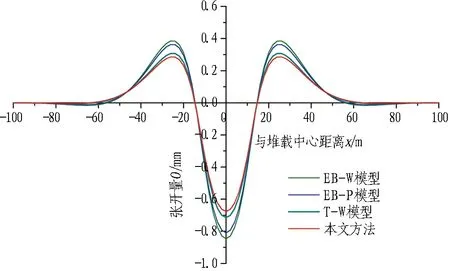
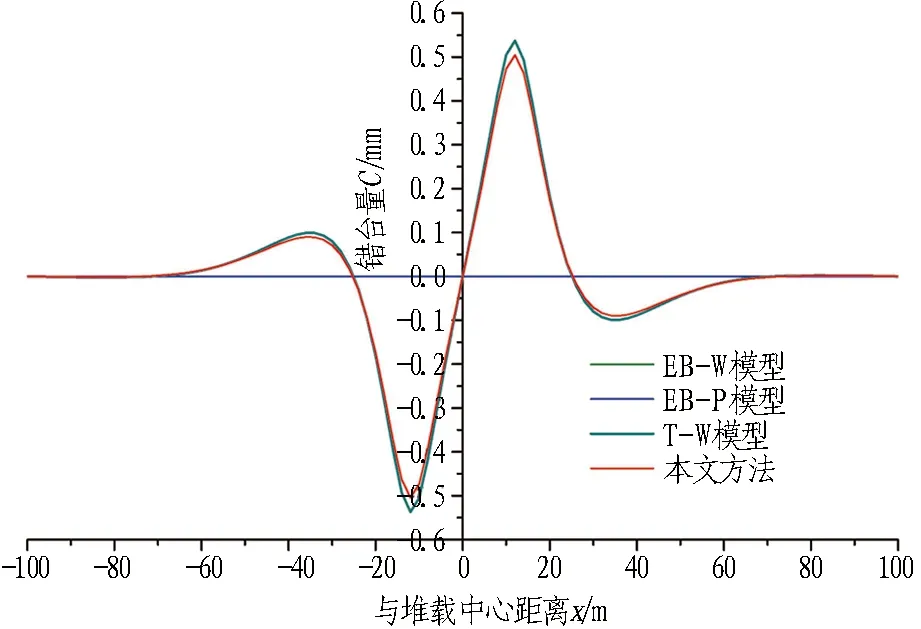
由图6(c)和6(d)可知，接头张开量、管片错台量分布图分别与隧道弯矩、剪力分布图变化趋势一致，其原因为接头张开量、管片错台量分别由隧道弯矩、剪力控制(式(14)和式(18))。根据图6(d)，2种基于Euler-Bernoulli梁的计算模型假定盾构隧道剪切刚度无穷大，不考虑剪切效应，因此无法计算管片错台量； 而本文T-P模型及T-W模型所得管片错台量最大值差别较小，约为0.5 mm，位于隧道最大剪力出现位置，即堆载边界(±12 m)处，可见Timoshenko梁模型更接近隧道变形的真实状态。根据本文模型算得接头最大张开量为0.7 mm，略小于Euler-Bernoulli模型计算结果0.8 mm。

4 影响因素分析

为了分析盾构隧道竖向变形与几个关键变量之间的关系，建立下述工程案例： 在地面进行堆土施工，简化堆土为矩形均布荷载，其大小为p=100 kPa，矩形荷载长l=24 m、宽B=50 m，堆载中心到隧道轴线的距离为d(水平方向)，隧道深度z0=10 m，堆载与隧道位置关系如图1所示。隧道相关参数如前文所述，隧道等效抗弯刚度(EI)eq=7.8×107kN·m2，等效剪切刚度(κGA)eq=2×106kN/m。土层弹性模量为Es=10 MPa，泊松比ν=0.33。

(a) 弯矩M

(b) 剪力Q

(c) 接头张开量O

(d) 管片错台量C

4.1 荷载位置的影响

图7示出堆载与隧道之间水平距离d对隧道竖向变形w的影响。可以看出，当地面堆载位于隧道正上方时，隧道竖向变形最大，变形最大值达到33.2 mm； 随着距离d的增大，隧道竖向变形逐渐减小，即地面堆载距隧道轴线越远，对隧道变形的影响越小。当d≥0.7B(B=50 m)时，地面堆载对隧道竖向变形影响较小，隧道最大竖向变形此时仅为2.6 mm。现行GJJ/T 202—2013《城市轨道交通结构安全保护技术规范》[28]规定建设施工导致的“隧道竖向变形的预警值为10 mm，控制值为20 mm”。由图7可知，当d≤0.4B(B=50 m)时，隧道最大竖向位移w>20 mm，超过了规范限值，存在安全隐患，应在施工过程中予以重视。此外，隧道竖向变形(沿轴线)主要集中在隧道轴线两侧±40 m(3～4倍加载宽度)，地面堆载对隧道轴线两侧40 m范围以外的隧道结构影响很小，基本可以忽略。

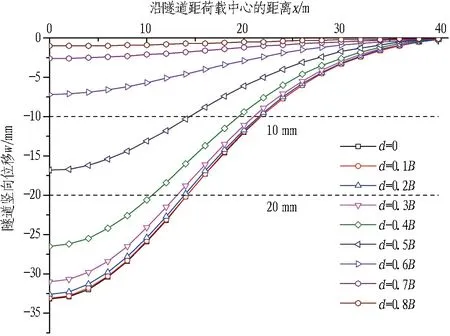
图7 堆载与隧道之间水平距离d对隧道竖向变形w的影响

4.2 土层弹性模量的影响

图8示出土层弹性模量Es对隧道最大竖向变形wmax的影响。本文理论计算基于Pasternak地基模型，Pasternak模型中2个关键参量基床反力系数k和地基剪切刚度Gs均由土层弹性模量Es导出。由图8可得，随着土层弹性模量提高，隧道最大竖向变形不断减小，这是由于土层弹性模量的增大使得基床反力系数k和地基剪切模量Gs都变大，地基刚度增强，因而隧道变形量减小。此外，从图8中还可以发现，当Es≤14 MPa时，随着隧道所在土层Es的提高，隧道变形量显著减小，即当土层较软弱时，隧道变形对土层弹性模量的增大响应明显。实际工程中，可以采取通过对土层进行人工加固的方法减小堆载对隧道结构变形的影响，软土地区的加固效果更突出。

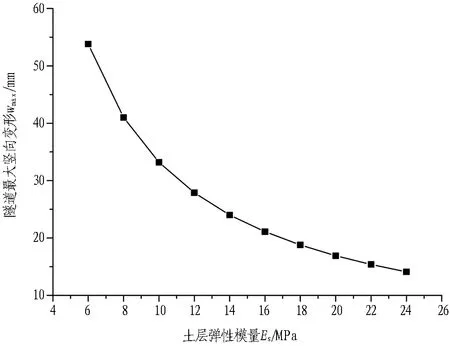
图8 土层弹性模量Es对隧道最大竖向变形wmax的影响

4.3 隧道等效抗弯刚度和等效剪切刚度的影响

图9示出隧道等效抗弯刚度(EI)eq和等效剪切刚度(κGA)eq对隧道最大竖向变形wmax的影响。由图9可知，在等效抗弯刚度一定的情况下，随着等效剪切刚度(κGA)eq的增大，隧道最大竖向变形不断减小，但当(κGA)eq超过2×106kN/m后，隧道最大竖向变形变化很小； 当(κGA)eq趋于无穷大时，本文T-P模型退化为不考虑盾构管片接头对隧道整体刚度削弱的EB-P模型，此时隧道最大竖向变形将达到最小值。可见，一味增大管片接头处剪切刚度并不能有效减小隧道竖向变形。由图9还可以发现，在隧道等效剪切刚度(κGA)eq一定的情况下，随着隧道等效抗弯刚度(EI)eq的增大，隧道最大竖向变形不断减小。相较于等效剪切刚度(κGA)eq，等效抗弯刚度(EI)eq的增大对隧道竖向变形的影响更为显著。

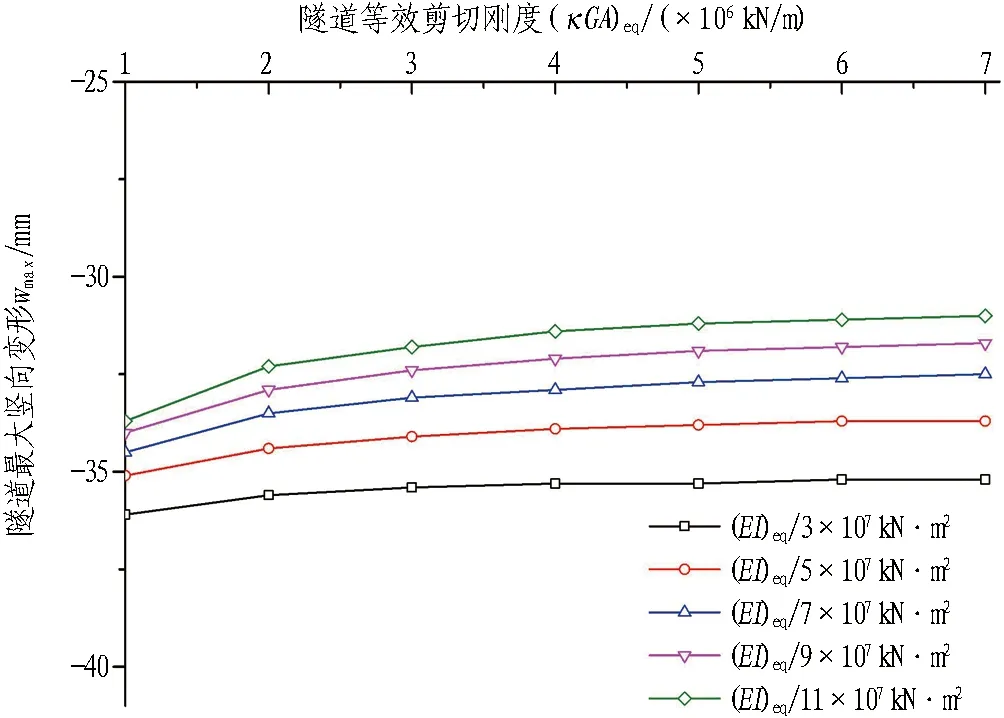
图9 隧道等效抗弯刚度(EI)eq和等效剪切刚度(κGA)eq对隧道最大竖向变形wmax的影响

5 结论与讨论

1)本文将盾构隧道简化为置于双参数Pasternak地基上的Timoshenko梁(T-P模型)，T-P模型可以考虑盾构隧道的剪切变形效应以及地基变形的连续性，能够得到堆载引起的隧道纵向变形，以及隧道纵向弯矩、剪力、接头张开量和管片错台量的分布。

2)对比实际工程监测数据与理论模型计算结果，在实测数据的最大值附近，本文理论模型计算结果相比其他模型计算结果与实测数据更为吻合，从而验证了本文模型的可靠性。

3)在隧道纵向变形计算上，本文提出的T-P模型相比常用的Euler-Bernoulli梁模型计算结果较大，而稍小于T-W模型计算结果，更接近实际监测数据；在内力计算上，Euler-Bernoulli梁模型计算结果较大，常用的EB-W模型弯矩、剪力最大值均为本文T-P模型的1.3倍。

4)参数分析发现，盾构隧道的变形受地面堆载相对位置、土层弹性模量以及隧道等效抗弯刚度影响较大，随着堆载与隧道之间水平距离、土层弹性模量以及隧道等效抗弯刚度的增大，隧道竖向变形逐渐减小； 而盾构隧道的变形对隧道等效剪切刚度的变化不敏感，当等效剪切刚度超过2×106kN/m时，隧道最大竖向变形随等效剪切刚度的增加变化很小。

由于技术所限，目前还缺少隧道纵向受力的相关监测数据，因此，本文只是将基于理论模型的隧道受力结果与其他模型隧道受力结果进行横向对比分析，而缺少与实测数据的对比，这部分内容还有待做进一步的研究。