弓形和矩形先导级2D伺服阀动态特性分析

陈 烜 阮 健 刘 奎 朱兆良 赵 伟 李 胜

(1.浙江工业大学二维(2D)液压/气动元件及系统工程技术研究中心， 杭州 310023；2.嘉兴学院机电工程学院， 嘉兴 314001)

0 引言

电液比例/伺服控制系统因其输出功率大、结构紧凑以及优良的静动态特性而广泛应用于工业及工程自动化装备中[1-2]。随着自动化技术的发展，对电液伺服控制系统提出了更高要求，比如更高的工作压力、良好的抗污染能力和可靠性等[3]。

电液比例/伺服阀作为电液比例/伺服控制系统的核心元件，其静动态特性基本决定了整个系统的特性[4-7]。为了克服液动力，实现高压、大流量控制，绝大多数的电液伺服(比例)阀采用多级结构。典型的两级电液伺服阀由先导级和功率级构成，先导级结构主要有喷嘴-挡板式、射流管式和滑阀式[8]。喷嘴-挡板式伺服阀先导级的喷嘴与挡板间的环形面积构成可变节流口，但喷嘴和挡板间的间隙仅0.03～0.05 mm[9], 易堵塞，因此该类伺服阀的进油口必须加装滤油装置。射流管式伺服阀先导级可变节流口的节流面积为喷嘴和接收孔间的重叠面积，由于喷嘴和接收孔间隙较大，因此与喷嘴-挡板式伺服阀相比，电液伺服阀的抗污染能力得以改善[10]。先导级为滑阀(转阀)，可设计成电液伺服阀或者比例阀，前者一般采用高频响的音圈电机作为电-机械转换器，后者一般采用比例电磁铁作为电-机械转换器。此外，在系统压力不高或流量较小的场合，也可以采用大功率的电-机械转换器构成直驱式电液伺服阀或比例阀，如采用大功率马达或者比例电磁铁作为电-机械转换器的直驱式伺服阀[11-12]，也可以采用音圈电机作为电-机械转换器构成直驱式的电液伺服阀[13]，或者采用旋转电机驱动的直驱式电液伺服阀[14-15]。

RUAN等[16]基于2D螺旋伺服原理提出2D伺服阀结构，利用阀芯转动自由度和直动自由度，将先导级和功率级集成在单个阀芯上，其结构紧凑，可满足高压大流量的要求，同时具有很高的抗污染能力(达到NAS11级)。采用电机作为电-机械转换器，构成2D电液数字伺服阀，成功地应用于新一代战机的液压控制系统中。2D电液数字伺服阀的先导级节流口形状为弓形[17]，采用电机通过传动机构驱动阀芯旋转角较大[18]，因此弥补了弓形先导级流量增益的不足，保证了阀的响应速度。2D数字伺服阀由于存在传动机构，导致整体结构复杂，另外，传动机构间存在间隙使得阀的滞环增大[19]。为此采用力矩马达作为电-机械转换器，将衔铁和阀芯固连，直接驱动阀芯转动[20-21]。由于力矩马达的转角很小，若2D伺服阀仍采用弓形的先导级开口，其先导级流量增益无法满足整个阀快速响应的要求，因此有必要对先导级节流口开口形式进行研究。

本文对弓形和矩形两种先导级结构的2D伺服阀动态特性及其结构参数对动态特性的影响进行研究。首先，阐述2D伺服阀的结构及工作原理，分别建立弓形和矩形先导级2D伺服阀的数学模型，采用数值计算的方法对两者进行仿真分析，获得在不同结构参数(斜槽角β、先导级零位开口量h0、系统压力ps)下的阶跃响应特性；然后，搭建2D伺服阀的阶跃响应特性实验平台，获得两类先导级结构2D伺服阀的阶跃响应特性实验曲线，并与仿真结果进行比较；最后，将弓形2D伺服阀用于力矩马达驱动的2D电液伺服阀中，测试其阶跃响应特性。

1 2D伺服阀结构及工作原理

2D伺服阀结构及工作原理如图1所示。2D伺服阀阀芯具有转动和直动两个运动自由度，其中阀芯转动起到先导级的作用，阀芯直动起到功率级的作用。2D伺服阀阀芯最左端台肩上有两对高低压油口，其中高压油口通过阀芯内部油道与系统压力相连通，低压油口与低压腔相沟通。在高低压油口之间的位置，阀套内表面开有斜槽与阀芯左端的敏感腔相连。从而使得斜槽、高压油口和低压油口三者共同构成一个液压阻尼半桥，控制敏感腔压力pc。

图1 2D 伺服阀结构及工作原理图

在稳态条件下，高压油口与斜槽重叠形成的开口面积A1和低压油口与斜槽重叠形成的开口面积A2相等，敏感腔的压力pc为系统压力ps的一半，由于阀芯左侧敏感腔静压力作用面积As为右侧高压油腔静压力作用面积Ar的两倍，同时阀芯受到的摩擦力和伯努利力相比阀芯两端的静压力可以忽略不计，因此pcAs=psAr，阀芯处于静压平衡。

当电-机械转换器驱动阀芯转动角θ时，高压油口开口面积A1与低压油口开口面积A2不再相等，导致敏感腔压力pc发生变化，稳态条件下的阀芯静压力平衡被打破，此时阀芯在静压力作用下产生轴向位移。阀芯在轴向运动过程中，由于阀套内表面斜槽的存在，高压油口开口面积A1与低压油口开口面积A2逐渐恢复相等，敏感腔压力pc重新达到系统压力ps的一半，最终阀芯在静压力作用下，稳定在轴向位移xv处，实现对负载流量的控制。

图1圆圈中是2D伺服阀的先导级结构，为了研究2D伺服阀先导级结构形式(弓形和矩形)及其结构参数对2D伺服阀动态特性的影响，给出弓形和矩形2D伺服阀两种先导级结构。

图2为2D伺服阀弓形先导级结构，即阀套内表面斜槽分别与高压油口和低压油口重叠形成的先导级可变节流口的形状为弓形(一定情况下会变成圆形)。图3为2D伺服阀矩形先导级结构，即阀套内表面斜槽分别与高压油口和低压油口重叠形成的先导级可变节流口形状为矩形。

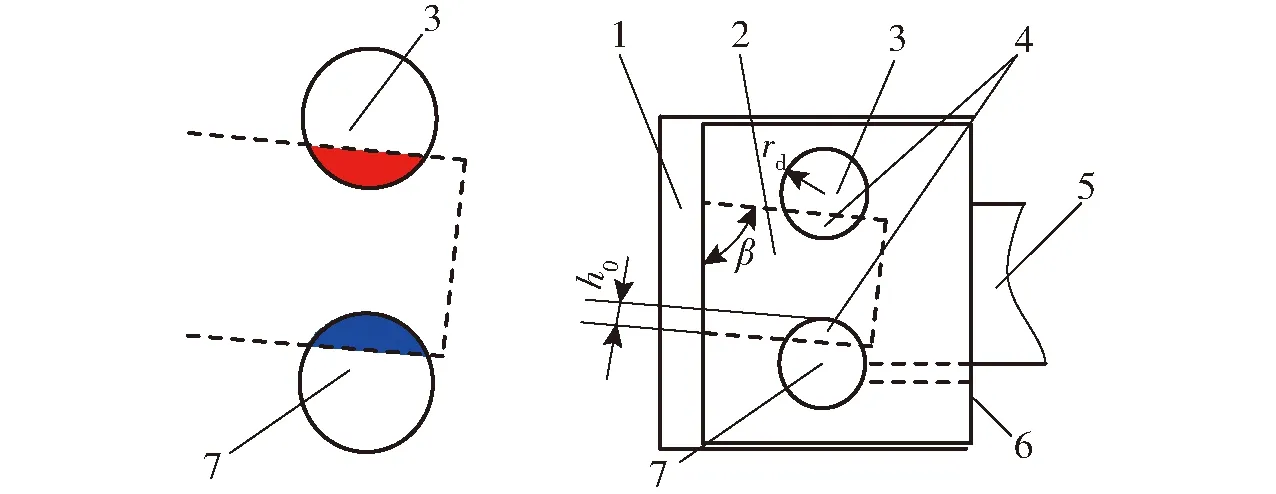
图2 2D 伺服阀弓形先导级结构

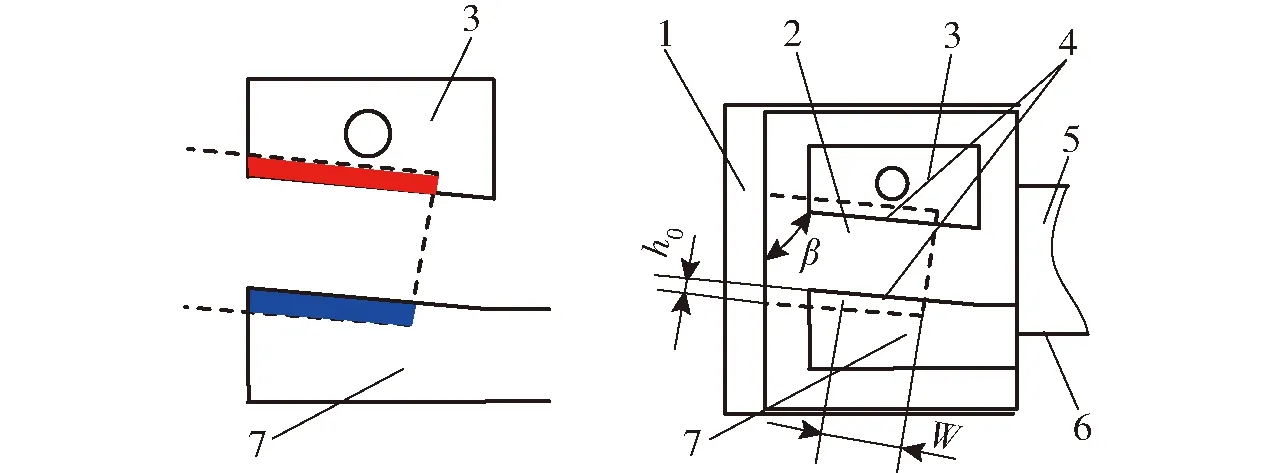
图3 2D伺服阀矩形先导级结构

2 2D伺服阀数学模型

由于阀芯左侧台肩开有一对高低压油口，即有2个高压油口和2个低压油口，因此流出高压油口的流量为

(1)

式中Cd——流量系数，取0.61

ρ——油液密度

同理，流进低压油口的流量为

(2)

由图2和图3可知，本文两种2D伺服阀先导级结构形式，各自的高低压油口开口面积A1和A2的表达式需要分情况讨论。

若2D伺服阀先导级可变节流口形状为弓形(图4)，则高压油口开口面积为

(3)

其中

h1=h0+Δh

式中h1——开口面积A1的开口量，即弓形可变节流口开口面积的弓高

h0——初始开口

Δh——开口量的变化量

rd——高低压油口半径

同理低压油口开口面积为

(4)

其中

h2=h0-Δh

式中h2——开口面积A2的开口量，即弓形可变节流口开口面积的弓高

若2D伺服阀先导级可变节流口形状为矩形(图5)。则高压油口开口面积为

(5)

式中W——高低压油口面积梯度

同理低压油口开口面积为

(6)

图4 弓形先导级2D伺服阀示意图

图5 矩形先导级2D伺服阀示意图

由图4和图5可知，当电-机械转换器驱动阀芯逆时针方向旋转时,h1和h2表示为

(7)

式中R——阀芯最左端台肩半径

β——斜槽倾角

若不考虑阀芯最左端台肩与阀套间的间隙泄漏流量, 根据2D伺服阀先导级流量连续性方程可得

(8)

式中Vt——敏感腔体积

βe——液压油的体积弹性模量

忽略伯努利力及摩擦力的影响,2D伺服阀阀芯的力平衡方程为

(9)

式中ms——2D伺服阀阀芯质量

Bs——阻尼系数Ks——弹性模量

FL——作用在阀芯上的外界干扰力

由式(1)、(2)、(8)、(9)共同构成2D伺服阀的基本方程，通过求解可以获得2D伺服阀的动态特性。

在先导级零位附近线性化处理式(1)和式(2)，式(8)可变为

(10)

式中Kq——2D伺服阀先导级流量增益

Kc——2D伺服阀先导级流量-压力系数

若为矩形先导级2D伺服阀，则

(11)

(12)

且W为恒值。

若为弓形先导级2D伺服阀，在零位附近，有

(13)

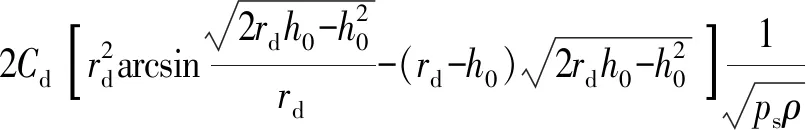
(14)

2D伺服阀的结构组成类似一个阀控缸系统，先导级结构类似阀控缸系统中的控制滑阀，而功率级结构类似阀控缸系统中的液压缸，2D伺服阀先导级的流量增益Kq直接影响功率级阀芯轴向运动的响应速度，同时2D伺服阀先导级的流量-压力系数Kc会直接影响阀芯轴向运动的阻尼比。

3 2D伺服阀动态特性方程求解

3.1 动态特性的数值求解

由于弓形和矩形先导级2D伺服阀的基本方程都为结构复杂的常微分方程，很难求得解析解，因此本文采用数值解法，即经典龙格-库塔法[22]求取弓形和矩形先导级2D伺服阀的动态响应。

数值计算中的弓形先导级2D伺服阀和矩形先导级2D伺服阀参数如表1所示。

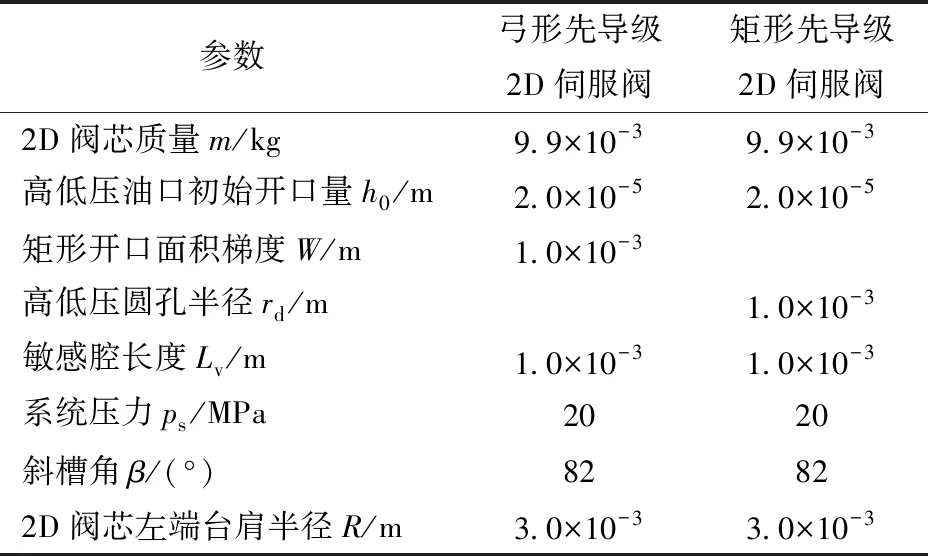
表1 2D伺服阀参数

弓形及矩形先导级2D伺服阀阶跃响应的数值计算结果如图6所示，弓形先导级2D伺服阀的阶跃响应时间为3.48 ms, 矩形先导级2D伺服阀的阶跃响应时间为1.4 ms,在相同主要结构参数(斜槽角β、先导级零位开口量h0、系统压力ps)条件下，矩形先导级2D伺服阀阶跃响应速度远快于弓形先导级2D伺服阀。

图6 弓形及矩形先导级2D伺服阀的阶跃特性(数值计算)

由表1可知rd远大于h0,因此式(13)可简化为

(15)

根据表1和式(11)，此时在零位附近，矩形先导级流量增益大于弓形先导级流量增益。由于先导级的流量增益Kq决定了阀芯的轴向位移响应速度。因此使得矩形先导级2D伺服阀阶跃响应速度远快于弓形先导级2D伺服阀。若为了提高弓形先导级2D伺服阀的响应速度需增大rd，但此时rd的尺寸会受到阀芯台肩尺寸限制。

3.2 结构参数对动态特性的影响

采用经典龙格-库塔法研究结构参数(斜槽角β、先导级零位开口量h0、系统压力ps)对弓形以及矩形先导级2D伺服阀动态特性的影响。

斜槽角β对矩形以及弓形先导级2D伺服阀动态特性的影响如图7所示。在阀芯轴向位移xv相同的条件下，弓形先导级2D伺服阀阶跃响应时间随斜槽角β的增大而增大，矩形先导级2D伺服阀阶跃响应时间随斜槽角β的增大而减小(图7)。

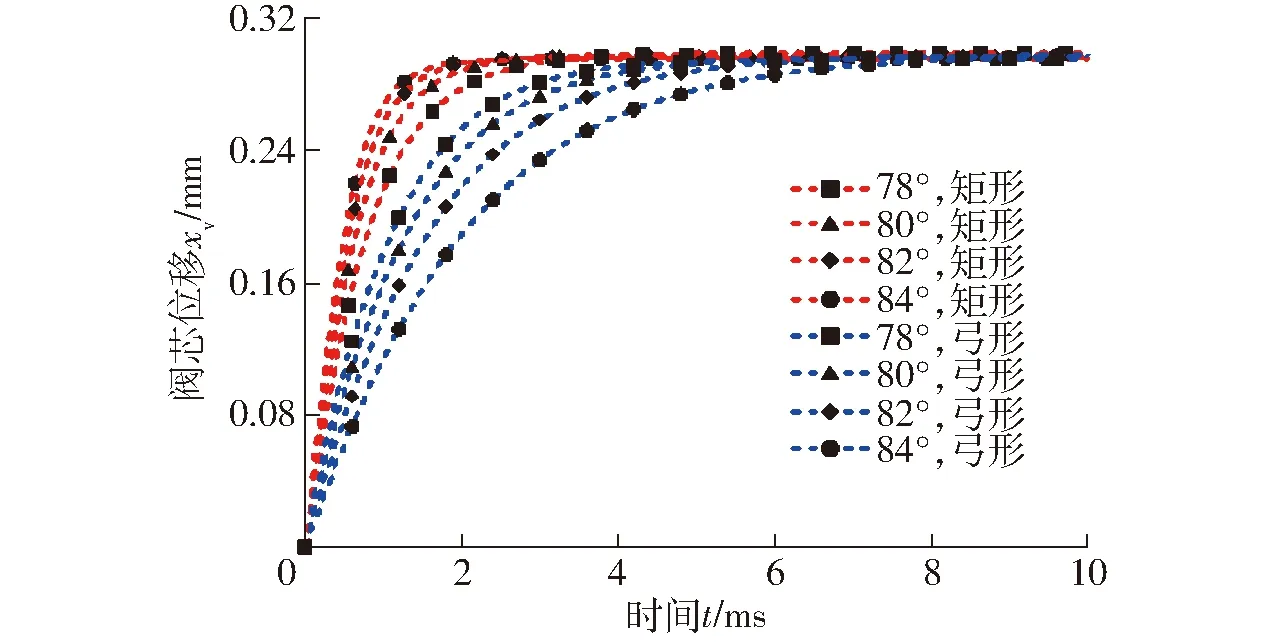
图7 不同斜槽角β下的2D伺服阀阶跃特性(数值计算)

由于阀套内表面斜槽角β的存在，对阀芯轴向位移xv产生位置反馈，因此当阀芯达到稳态时，斜槽角β与阀芯轴向位移xv存在几何关系，即

xv=Rθtanβ

(16)

在保证阀芯轴向位移xv不变的情况下，若斜槽角β增大时，阀芯所需的转角θ就减小。弓形先导级2D伺服阀在小角度(小于2°)驱动阀芯转动条件下，制约其响应速度的主要因素是Kq，随着斜槽角β的减小，转角θ增大，使得流量增益增大，阀芯轴向位移xv响应速度加快。而矩形先导级2D伺服阀制约其响应速度的主要因素是转角θ，当斜槽角β增大时，转角θ行程缩短，所需的响应时间更短。

图8 不同先导级零位开口量h0下的2D伺服阀阶跃特性(数值计算)

先导级零位开口量h0对矩形以及弓形先导级2D伺服阀动态特性的影响如图8所示。当先导级零位开口量h0在区间0～0.02 mm增大时，矩形以及弓形先导级2D伺服阀的阶跃响应时间随h0增大而减小，但h0的增大使系统响应加快的同时，也会导致零位泄漏的增加。同时由图8可知，当先导级零位开口量h0逐渐接近0时，矩形先导级2D伺服阀阀芯的稳定性变差，产生振荡的现象，由式(12)可知，矩形先导级2D伺服阀先导级的流量-压力系数Kc与h0成正比，同时2D伺服阀先导级的流量-压力系数直接影响阀芯轴向运动的阻尼比。若h0趋向于零，矩形先导级流量-压力系数也会趋向于零，导致其提供的阻尼减小，使得系统稳定性下降产生振荡。另外矩形先导级2D伺服阀在相同先导级零位开口条件下，响应时间小于弓形先导级2D伺服阀，甚至在h0为零的条件下，矩形先导级2D伺服阀的响应时间小于h0为0.02 mm下弓形先导级2D伺服阀的响应时间(图8)。

系统压力ps对矩形和弓形先导级2D伺服阀阶跃响应的影响如图9所示。当系统压力ps在5～20 MPa区间内，矩形以及弓形2D伺服阀阶跃响应时间都随系统压力ps增大而减小。同时矩形2D伺服阀在相同系统压力ps条件下，响应时间小于弓形2D伺服阀，甚至在系统压力5 MPa条件下矩形2D伺服阀的响应时间小于20 MPa下弓形2D伺服阀的响应时间(图9)。

图9 不同系统压力ps下的2D伺服阀阶跃特性(数值计算)

4 实验与结果分析

4.1 摆轮法测2D伺服阀的阶跃特性

由矩形以及弓形先导级2D伺服阀动态特性的数值仿真结果可知，2D伺服阀的阀芯轴向位移xv对阀芯转角θ的响应速度极快，仅有几毫秒。实验中转角为0.8°，理想条件下要求其转角的响应时间趋向零，但阀芯本身存在一定的转动惯量，实际无法做到转角信号θ响应时间绝对为零。为此本文采用摆轮法测2D伺服阀的阶跃特性，通过直流电机带动凯夫拉线快速拉动阀芯转动，使得阀芯转角信号的响应时间趋近于零。

图10为摆轮法测2D伺服阀阶跃特性的实验原理，相应的实验装置如图11所示。由于直流电机(最大转速约6 000 r/min)启动达到最大速度需要一定的响应时间，为了获得2D 伺服阀转角θ极短的响应时间，采用直流电机驱动主动轮，当电机达到最高速度时，从动轮上缠绕凯夫拉线被主动轮绕完，进而通过凯夫拉线拉动摆杆，产生实验所需的阀芯转角θ的阶跃输入信号。摆杆两端的限位块用于限制阀芯的转角θ。实验台有2台激光位移传感器(Keynes LK-G150H型，分辨率为0.6 μm)，其中激光位移传感器Ⅰ用于采集阀芯的转角信号θ，即用小角度的线位移替代角位移。激光位移传感器Ⅱ用于采集阀芯的轴向位移信号xv。实验使用AgilentDSO6014A型数字示波器，其有4个输入通道，本实验用2个通道，分别显示和记录阀芯的转角信号θ和轴向位移信号xv。

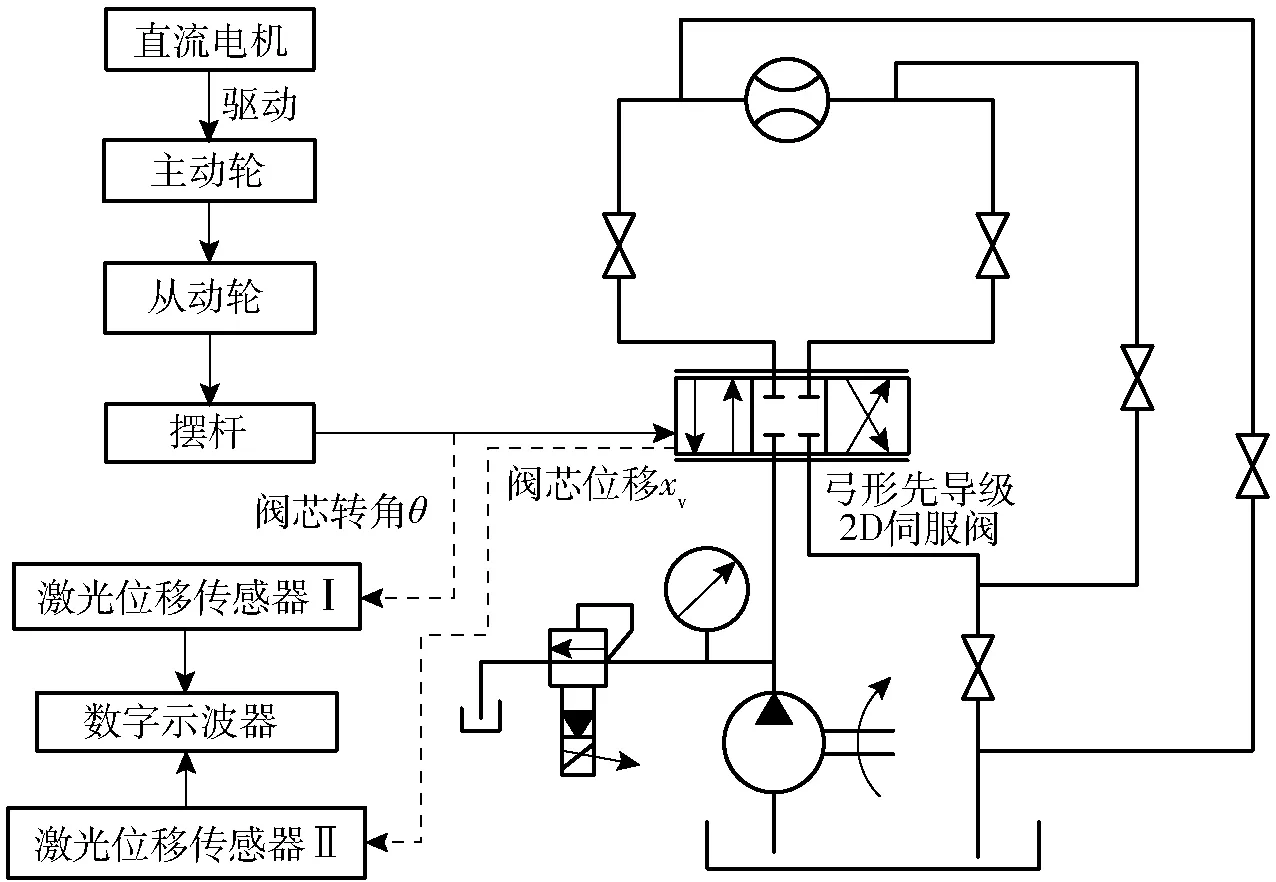
图10 摆轮法测2D伺服阀阶跃特性实验原理图

图11 摆轮法测2D伺服阀动态特性响应实验装置图

同时实验中系统压力ps为20 MPa,矩形先导级2D伺服阀和弓形先导级2D伺服阀阀套内表面的斜槽角β均为82°，高低压油口的初始开口量h0均为0.02 mm。

图12为矩形先导级2D伺服阀和弓形先导级2D伺服阀的阶跃响应实验曲线。其中矩形先导级2D伺服阀的响应时间为1.4 ms,弓形先导级2D伺服阀的响应时间为3.4 ms, 矩形先导级2D伺服阀的响应时间明显短于弓形先导级2D伺服阀，实验结果与数值仿真的结果基本吻合。但直流电机通过凯夫拉绳拉动阀芯转角的过程存在一定的响应时间，所以实验响应时间约0.1 ms。因此2D伺服阀阀芯轴向位移对阀芯转角的响应时间相比数值仿真稍长。

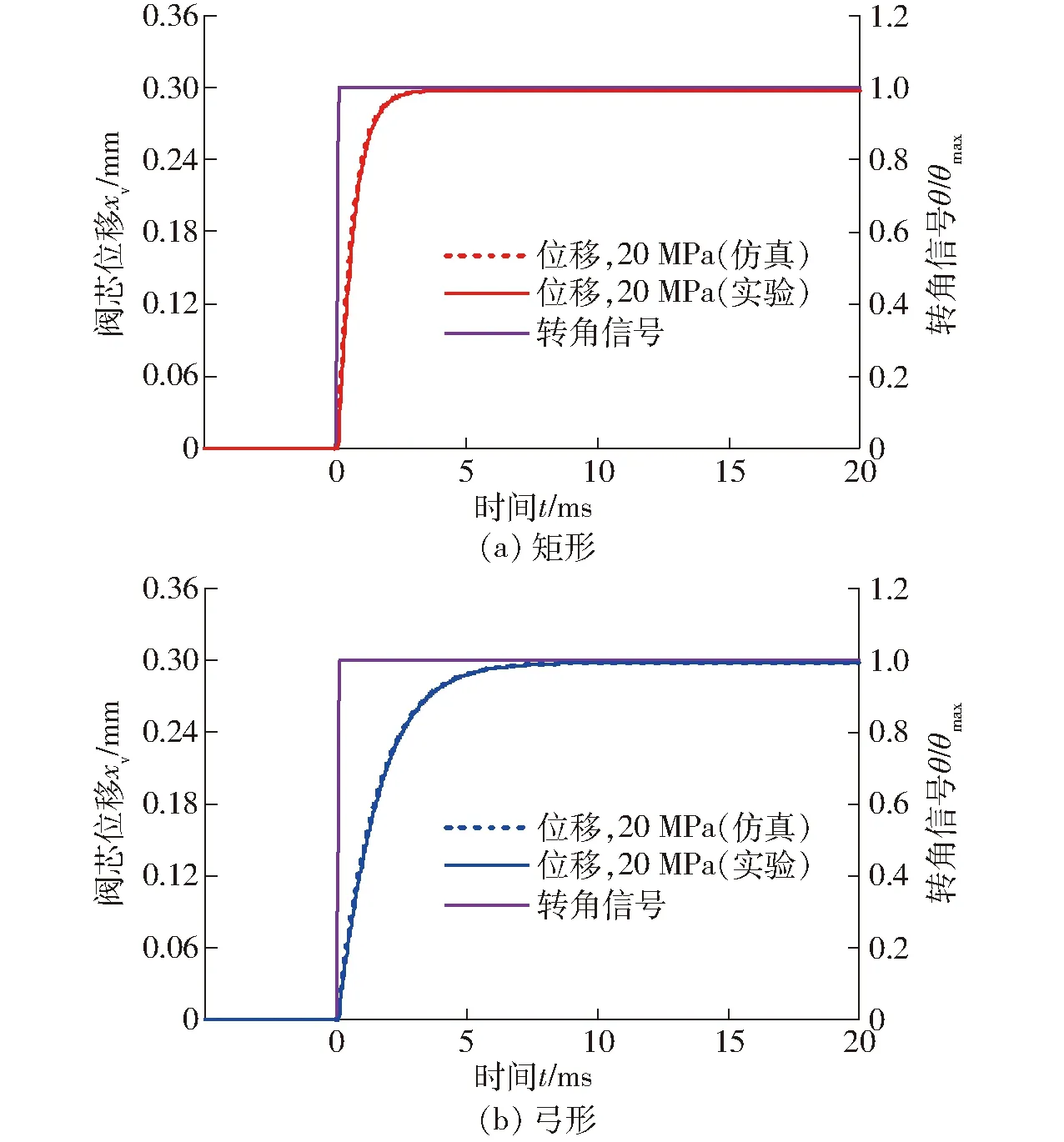
图12 不同先导级结构2D伺服阀阶跃特性实验曲线

4.2 力矩马达驱动2D伺服阀的阶跃特性

由于在阀芯转角θ极小并且相关结构参数(斜槽角β、先导级零位开口量h0、系统压力ps)相同的情况下，矩形先导级2D伺服阀阀芯轴向位移xv对阀芯转角θ的响应速度明显快于弓形先导级2D伺服阀，因此矩形先导级结构适用于力矩马达小角度驱动的2D电液伺服阀。

为了验证力矩电机驱动矩形先导级2D伺服阀的可行性，搭建图13所示力矩电机驱动矩形先导级2D伺服阀阶跃特性实验台，图14为相应的实验装置图。实验中系统压力ps为20 MPa，所用矩形先导级2D伺服阀阀套内表面斜槽角β为82°，先导级零位开口量h0为0.02 mm。

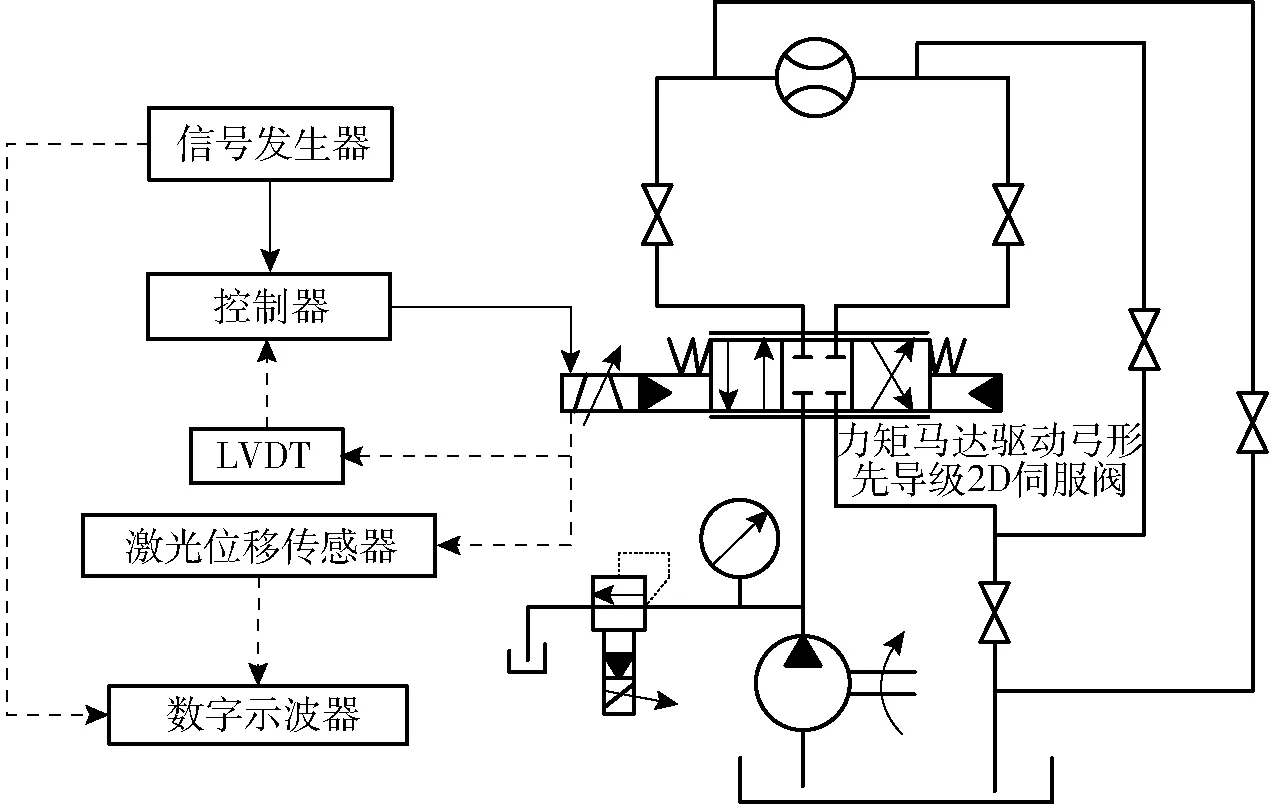
图13 力矩电机驱动2D电液伺服阀阶跃特性实验原理图

图14 力矩电机驱动矩形先导级2D电液伺服阀阶跃特性的实验装置图

信号发生器用于输出实验用的阶跃信号(图13)，该信号经控制器功率放大后，输入到力矩马达中驱动矩形先导级2D伺服阀阀芯旋转。LVDT用于采集阀芯的位移信号xv，并反馈回控制器构成阀芯的位置闭环。激光位移传感器用于采集力矩马达驱动矩形先导级2D伺服阀阀芯轴向位移xv, 数字示波器用于记录阀芯轴向位移xv以及信号发生器发出的阶跃信号。

由图15可知，力矩马达驱动矩形先导级2D伺服阀在阀芯轴向位移xv为0.3 mm时，其阶跃响应时间为10 ms。由图16可得，力矩马达驱动矩形先导级2D伺服阀幅频宽为100 Hz，相频宽为80 Hz。

图15 力矩马达驱动矩形先导级2D电液伺服阀的阶跃特性实验曲线(xv=0.3 mm)

由于矩形先导级2D伺服阀的阶跃响应时间为1.4 ms(实际阀芯轴向位移xv对阀芯转角θ需要消除转角的响应时间),因此阀部分的响应时间占整个力矩马达驱动矩形先导级2D电液伺服阀阶跃响应时间的14%。若仍采用早期2D伺服阀的弓形先导级结构，会大大减慢整个2D电液伺服阀的响应时间。因此2D电液伺服阀在使用小角度电-机械转换器直接驱动的条件下，例如力矩马达，若为了保证响应速度，其2D伺服阀的先导级结构需采用矩形先导级结构, 使得在初始条件下即获得较大的流量增益Kq, 从而获得极短的阀芯轴向位移xv对阀芯转角θ需要转角的响应时间，进一步提高2D电液伺服阀整个系统的响应速度。

5 结论

(1)先导级的流量增益Kq决定了2D伺服阀的响应速度，且矩形先导级流量增益大于弓形先导级流量增益，在相同主要结构参数(斜槽角β、先导级零位开口量h0、系统压力ps)条件下，矩形先导级2D伺服阀阶跃响应速度优于弓形先导级2D伺服阀。

(2)在阀芯轴向位移xv相同的条件下，弓形先导级2D伺服阀阶跃响应时间随斜槽角β的增大而增大，矩形先导级2D伺服阀阶跃响应时间随斜槽角β的增大而减小；先导级零位开口量h0在一定范围内的增大，能够减小2D伺服阀的响应时间，同时当h0接近于零时，影响了2D伺服阀先导级的流量-压力系数Kc，造成系统阻尼比下降，从而降低了系统稳定性，矩形先导级2D伺服阀还出现了振荡现象；系统压力ps的增大可以提高2D伺服阀的响应速度。

(3)采用摆轮法获得弓形和矩形先导级2D伺服阀的阶跃响应实验曲线，与数值计算结果基本吻合。综合理论和实验结果表明，2D伺服阀采用矩形先导级结构，增大了先导级流量增益Kq，相比弓形先导级结构，能够进一步提高整个伺服阀的响应速度。

(4)将矩形先导级2D伺服阀用于力矩马达驱动2D伺服阀中，在阀芯轴向位移xv为0.3 mm时，其阶跃响应时间为10 ms。可以满足2D电液伺服阀在阀芯转角极小的条件下的响应速度要求。