2UPR-RPU过约束并联机构刚度性能评价

杨 超 叶 伟 张克涛 黄风立 张伟中

(1.嘉兴学院机电工程学院， 嘉兴 314001； 2.浙江理工大学机械与自动控制学院， 杭州 310018；3.伦敦玛丽女王大学工程与材料学院， 伦敦 E1 4NS)

0 引言

少自由度并联机构结构简单，具有高刚度性能和优异的动力学性能[1-2]。过约束并联机构是少自由度并联机构中的重要一类，过约束的存在可以提高机构刚度和消除奇异，过约束并联机构在重载或高精度要求场合下有着重要的应用，刚度性能是过约束并联机构的重要性能指标之一。

并联机构刚度建模的理论模型包括解析模型和半解析模型，对预设计阶段并联机构刚度性能的快速评估具有重要的作用。许多学者为此建立了多种刚度建模方法，包括虚铰方法、矩阵位移法、应变能方法和螺旋理论方法等。

虚铰方法将杆件当作两端由六自由度弹簧支撑的刚性杆件。ZHANG等[3]采用虚铰方法建立了Exechon过约束并联机构的刚度模型。WANG等[4]基于虚铰方法建立了Tricept并联机构的刚度模型，并考虑了铰链的柔度。虚铰方法需要处理冗余的弹簧约束，增加了刚度模型的复杂性[5-6]。矩阵位移法[7-8]将连杆作为一个梁单元处理，通过变形协调方程装配得到总体刚度矩阵。DEBLAISE等[9]采用矩阵位移法建立了Delta并联机构的刚度模型，KLIMCHIK等[10]介绍了矩阵位移法的基本原理，并建立了NaVaRo平面机构的刚度模型。矩阵位移法在有限元法的耗时性与解析方法的高效性之间取得了较好的权衡，计算精度较高。然而，矩阵位移法涉及矩阵的高维操作和大量的变形协调方程。螺旋理论方法基于螺旋理论得到分支的约束螺旋系，然后根据虚功原理得到机构的整体刚度矩阵，其优点是降低了分支约束螺旋系的维度，从而大大减少了变形协调方程的数目。文献[11-14]基于螺旋理论方法提出了分支约束螺旋系刚度矩阵的概念，建立了3-PRRR等并联机构的刚度模型，但建立分支刚度矩阵用了两次映射，增加了过程的复杂度。文献[15-17]基于螺旋理论方法建立了2PRU-UPR等并联机构的刚度模型，将分支约束螺旋系分解为梁的基本变形形式，思路简单，但却增加了分支刚度矩阵的维度，且模型中均未考虑剪切变形的影响和铰链的柔度。汪满新等[18]考虑重力的影响建立了3-RRS并联机构的刚度模型，得到了各构件刚度对末端刚度的影响。徐东涛等[19]考虑重力的影响建立了改进型Delta并联机构的刚度模型。利用应变能方法分析机构在外载荷作用下存储的应变能，结合卡氏定理建立机构的刚度模型，其优点是物理意义明确。文献[20-22]基于应变能方法建立了Delta和3-PSP等并联机构的刚度模型，但作者只考虑了受力较简单的非过约束机构，没有将应变能方法推广到过约束机构，YANG等[23]结合螺旋理论将应变能方法推广到过约束并联机构，建立了2PUR-PSR并联机构的刚度模型，然而却忽略了铰链的柔度。半解析方法[24]是通过有限元方法或厂家得到关节的刚度矩阵，由解析法得到连杆的刚度矩阵，然后通过变形协调方程装配得到机构的整体刚度矩阵，兼顾了解析法的高效率和有限元法的高精度。LIAN等[25]基于半解析法建立了T5并联机构的刚度模型。LIU等[26]考虑连杆和铰链的柔度建立了3-PRS并联机构的刚度模型。CAO等[27]考虑重力的影响建立了5-PRUR和4-RRRRR过约束并联机构的刚度模型，完善了计及重力影响的并联机构静弹性刚度模型。但以上研究成果中并没有得到各个弹性元件对机构刚度性能的影响程度。

本文基于应变能和螺旋理论建立2UPR-RPU过约束并联机构的刚度模型，同时考虑连杆和铰链的柔度。基于应变能的方法得到各个弹性元件对机构刚度性能的影响程度，以期为评价机构刚度性能影响最大的弹性元件提供思路，为提高机构的刚度性能提供新的方法。

1 机构描述

2UPR-RPU过约束并联机构如图1所示，动平台A1A2A3通过两个UPR分支和一个RPU分支与基座B1B2B3相连。参考坐标系建立如下：固定坐标系OXYZ的原点为B1B2的中点，X轴沿B1B2方向，Y轴沿OB3方向，Z轴由右手法则确定。动坐标系oxyz的原点为A1A2的中点，x轴沿oA2方向，y轴沿oA3方向，z轴由右手法则确定。分支坐标系Aixiyizi的原点为点Ai(i=1, 2, 3)，yi轴(i=1, 2)与y轴平行，x3轴与X轴平行，zi轴(i=1, 2, 3)沿着AiBi方向，xi轴(i=1, 2)和y3轴由右手法则确定。R铰坐标系oi1ui1vi1wi1与分支坐标系Aixiyizi相同(i=1, 2)，U铰坐标系o31u31v31w31与分支坐标系A3x3y3z3相同。U铰坐标系oi2ui2vi2wi2的原点为点Bi(i=1, 2)，ui2和vi2轴分别沿U铰的两根轴线方向，RPU分支R铰坐标系o32u32v32w32的原点为点B3，u32轴沿R铰轴线方向。对于两条UPR分支，R铰轴线与y轴平行，U铰的第1个轴线与B1B2共线，第2个轴线与另一端的R铰轴线平行。对于RPU分支，R铰轴线平行于X轴，U铰的第1条轴线与另一端的R铰轴线平行，第2条轴线与y轴平行。3个P副作为输入，并分别与R铰轴线垂直。这种特殊的安排使得机构具有3个自由度[28]：沿Oo的移动、绕X轴的旋转β和绕y轴的旋转γ。详细的运动学分析可参照文献[28]。

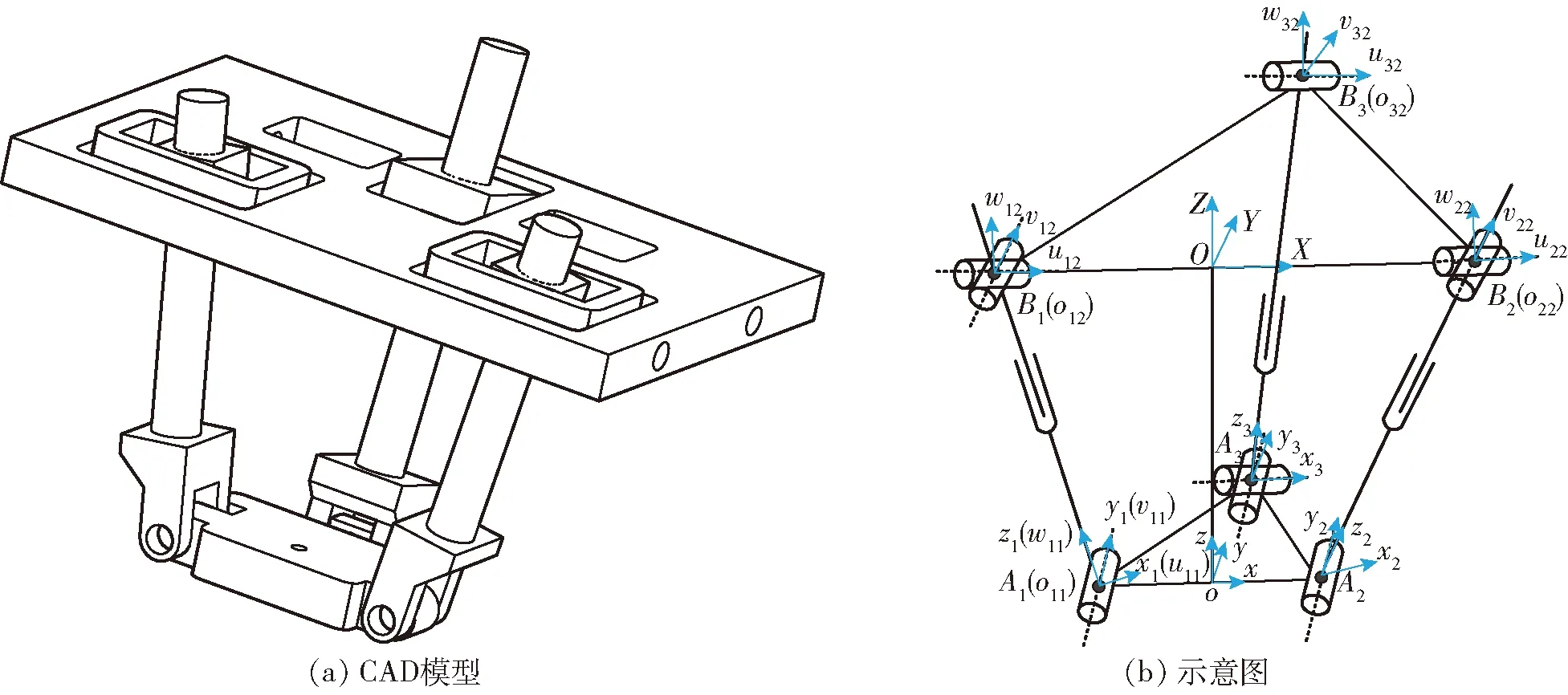
图1 2UPR-RPU并联机构

2 静弹性刚度模型

本文刚度模型作如下假设：忽略所有元件的质量和摩擦，驱动马达、基座和动平台假设为刚性。考虑关节的柔度以及杆件的轴向拉压、剪切、扭转和弯曲的空间复合弹性变形。

2.1 UPR分支刚度矩阵

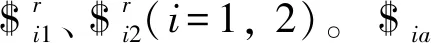
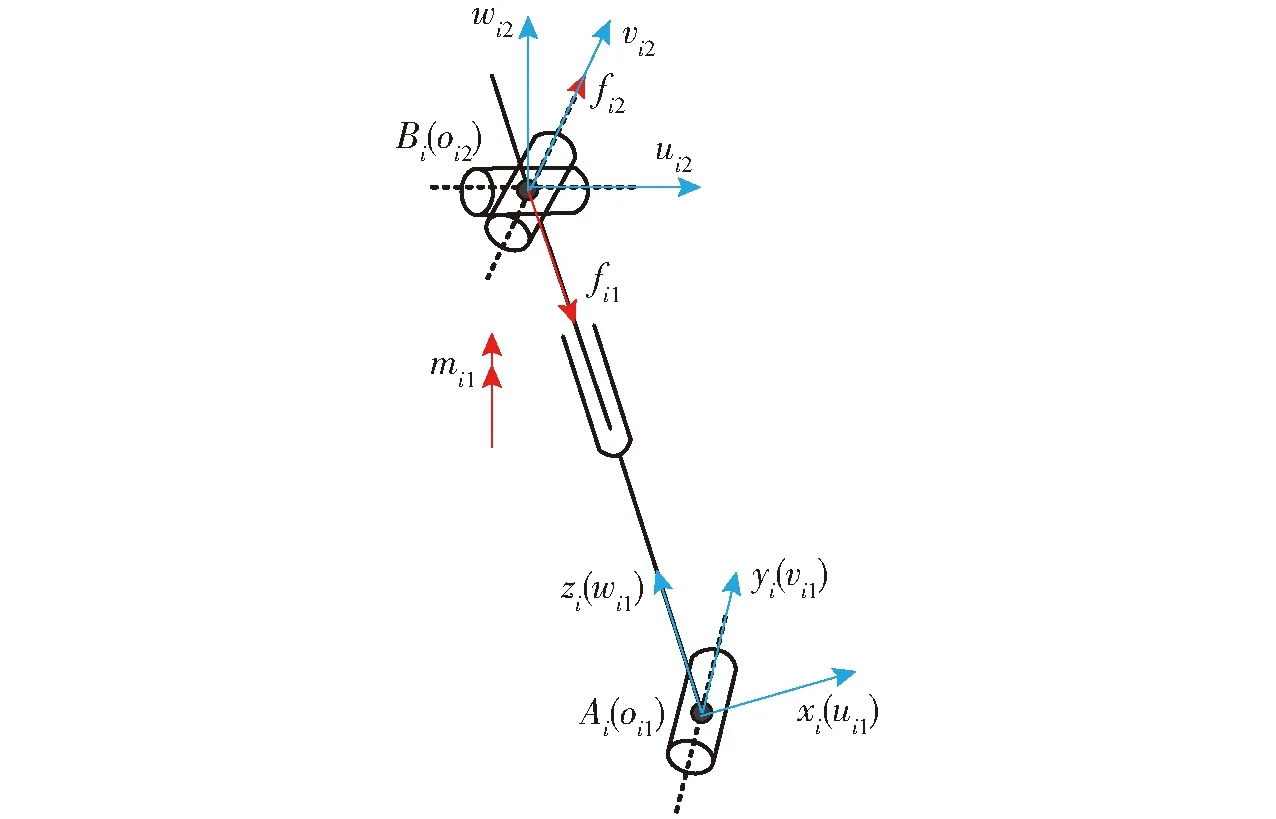
图2 UPR分支受力分析图

fi1、fi2和mi1的单位矢量定义为

(1)

式中li、X、yi——BiAi、X轴、yi轴的单位矢量

UPR分支任意截面处内力可表达为

(2)

式中Li——分支BiAi长度

杆件柔度矩阵可以由应变能和卡氏定理得到，杆件的柔度矩阵计算详见文献[29]，在此不再赘述。

杆件柔度矩阵为

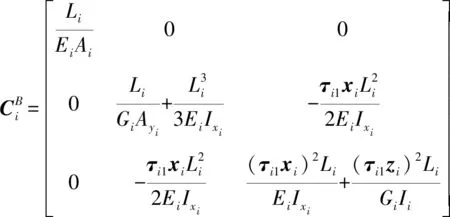
(3)

式中Ayi、Ai——截面沿yi轴的有效剪切面积和截面面积

Ei、Gi——杆件材料弹性模量和剪切模量

Ixi、Ii——截面对xi轴的惯性矩和截面极惯性矩

杆件应变能可以表达为

(4)

其中

Wi=[fi1fi2mi1]T

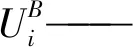
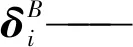
将Wi映射至R铰坐标系{oi1}的原点并在铰空间投影得到

(5)

其中oi1ui1=[1 0 0]oi1wi1=[0 0 1]

将式(5)进一步表达成矩阵形式为

oi1Wi=Di1Wi(i=1,2)

(6)

其中

(7)

oi1Wi=[oi1fui1oi1fvi1oi1fwi1oi1mui1oi1mvi1oi1mwi1]T

式中oi1Wi——坐标系{oi1}下6×1的矢量

Di1——从Wi到oi1Wi的 6×3映射矩阵

UPR分支R铰在自身铰空间的柔度矩阵可以由有限元方法[24-26]得到

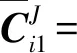
(8)

式中，前3项单位为m/N，后3项单位为rad/(N·m)。

因此，UPR分支R铰所存储的应变能可表达为

(9)

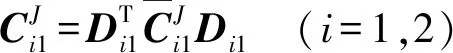
(10)

同样的方法，将Wi映射至U铰坐标系{oi2}的原点并在铰空间投影得到

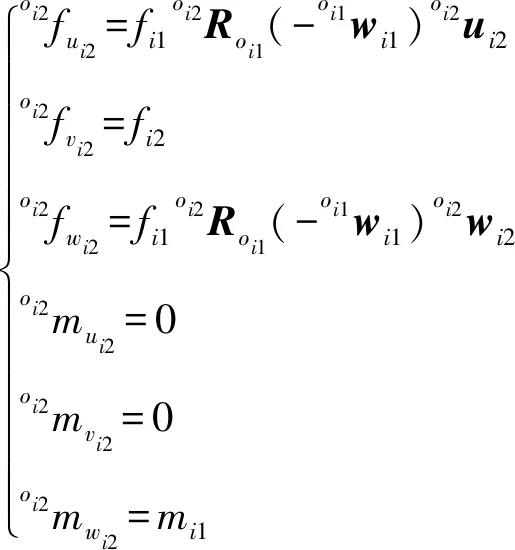
(11)

其中

oi2ui2=[1 0 0]oi2wi2=[0 0 1]

式中oi2Roi1——坐标系{oi1}到坐标系{oi2}的变换矩阵

式(11)可以进一步表达成矩阵形式为

oi2Wi=Di2Wi(i=1,2)

(12)

其中

(13)

oi2Wi=[oi2fui2oi2fvi2oi2fwi2oi2mui2oi2mvi2oi2mwi2]T

式中oi2Wi——坐标系{oi2}下6×1的矢量

Di2——从Wi到oi2Wi的6×3映射矩阵

UPR分支U铰所存储的应变能和U铰与约束螺旋系对应的柔度矩阵为

(14)

其中

(15)

其中，式(15)等号右侧前3项单位为m/N，后3项单位为rad/(N·m)。

UPR分支的应变能可以通过对杆件和铰链存储的应变能求和得到

(16)

UPR分支的紧凑刚度矩阵可以通过对式(16)中的柔度矩阵求逆得到

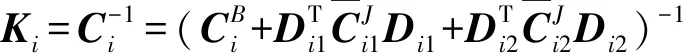
(17)

UPR分支与约束螺旋系对应的弹性变形可以由卡氏第二定理得

(18)

2.2 RPU分支紧凑刚度矩阵

图3 RPU分支受力分析图

f31、f32和m31的单位矢量定义为

(19)

式中l3——A3B3的单位矢量

x3、y3——沿x3、y3轴的单位矢量

同样的方法可以得到RPU分支杆件的柔度矩阵为

(20)

根据力的平移定理，将W3平移至U铰的中心并在铰空间坐标系{o31}下投影可以得到

o31W3=D31W3

(21)

其中

(22)

式中D31——从W3到o31W3的6×3映射矩阵

同理，将W3平移至R铰的中心并在铰空间坐标系{o32}下投影可以得到

o32W3=D32W3

(23)

其中

(24)

式中D32——从W3到o32W3的6×3映射矩阵

RPU分支的U铰和R铰在自身铰空间的柔度矩阵[24-26]分别为

(25)

与计算UPR分支应变能类似，RPU分支所存储的应变能可以表达为

(26)

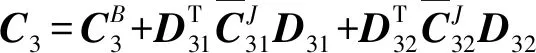
(27)

式中C3——RPU分支与约束螺旋系对应的分支紧凑柔度矩阵

对式(27)求逆即可得RPU分支紧凑刚度矩阵

(28)

由卡氏第二定理可以得到RPU分支与约束螺旋系对应的弹性变形

(29)

2.3 整体刚度矩阵

参考固定坐标系，2UPR-RPU并联机构动平台的平衡方程可以表达为

P=(J1J2J3)W=JW

(30)

其中

P=[F;M]

W=[W1W2W3]

式中P——作用在动平台的外部载荷

Ji——分支i的6×3约束螺旋系矩阵

J——6×9矩阵W——9×1矢量

F——作用在动平台的外力

M——作用在动平台的外力偶

动平台考虑为刚性，其虚功方程可以表达为

(31)

式中Δ——动平台与外部载荷P对应的弹性变形

联立方程(30)、(31)得

(32)

将方程(18)、(29)、(32)代入方程(30)得

(33)

(34)

式中K——机构的整体刚度矩阵

对方程(34)求逆可以得到机构的整体柔度矩阵

(35)

根据材料力学可得各分支约束螺旋系的幅值为

(36)

机构的总应变能可以表达为

(37)

3 理论模型与有限元模型对比

为了验证本文理论模型的正确性，采用ANSYS Workbench商业软件建立机构2个位型的有限元模型和理论模型作对比，位型1：z=-600 mm,β=0°,γ=0°，位型2：z=-600 mm,β=5°,γ=-3°，2个位型统一在o点施加外部载荷P=(30 N,-50 N,-40 N,10 N·m,-20 N·m,50 N·m)。2UPR-RPU并联机构物理参数为：lOB1=lOB2=lOB3=390 mm,loA1=loA2=loA3=260 mm,E1=E2=E3=210 GPa,G1=G2=G3=80 GPa,d1=d2=d3=100 mm，d1、d2和d3分别表示3个杆件的横截面直径。2UPR-RPU并联机构在两个位型下的变形云图如图4所示。表1给出了动平台o点的理论模型和有限元模型的变形量。由表1可知，理论模型与有限元模型的误差不大于7.8%，验证了理论模型的正确性，可用于物理样机在预设计阶段的刚度性能评估。

图4 2UPR-RPU并联机构变形量云图

表1 理论模型与有限元模型的计算结果对比

4 应变能因子指标

为了评价每一个弹性元件对机构整体刚度性能的影响程度，应变能因子指标定义为

(38)

式中μij——应变能因子指标，其表示每一个弹性元件存储的应变能与机构总应变能的比率，范围为0～1，μij越大表明此弹性元件存储的应变能越多

Uij——第i个分支的第j个弹性元件所存储的应变能

为了评价应变能因子指标在整个预规划工作空间的分布，全局应变能因子指标定义为

(39)

式中V——预规划工作空间体积

N——离散点数量

工程应用中，可以计算应变能因子指标在预规划工作空间的分布，有针对地提高应变能因子指标较大的元件的刚度性能，从而更有效地改善机构的刚度性能。

机构的规则工作空间受驱动的冲程、被动铰的角度限制以及杆件之间的干涉等因素的影响，2UPR-RPU并联机构的物理约束如下

(40)

式中αi1、αi2——R铰和U铰的旋转角

图5为空间搜索法得到的2UPR-RPU并联机构的可达和规则工作空间。由图5可以看出，可达工作空间关于γ=0对称，这与2UPR-RPU并联机构的结构分布一致，然而可达工作空间不规则，不利于轨迹规划和算法控制，并且机构在可达工作空间的边缘子空间的运动学性能和刚度性能也较差。不失一般性，本文采用空间内每一层的最大内切圆组成的圆台作为预规划的规则工作空间，为了保证一定的操作空间，最大内切圆的最小半径设置为10°。

图5 2UPR-RPU并联机构工作空间

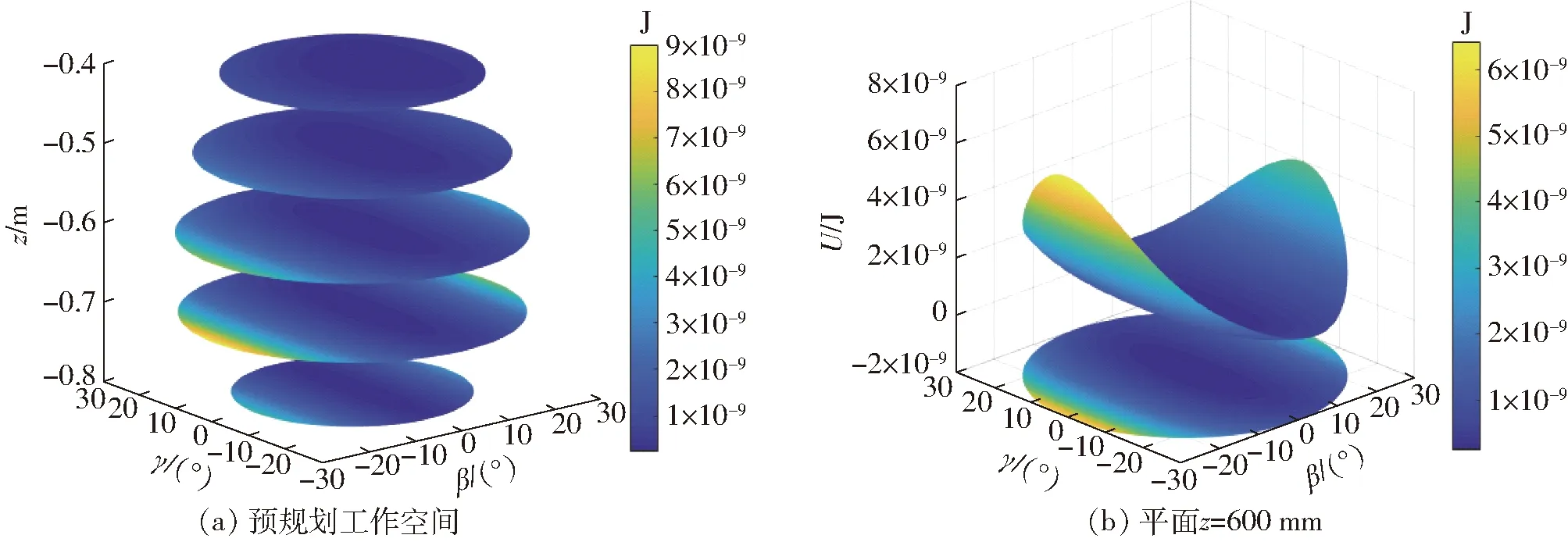
图6 P=P1时机构的总应变能的分布

图7 P=P1时μ在预规划工作空间的分布

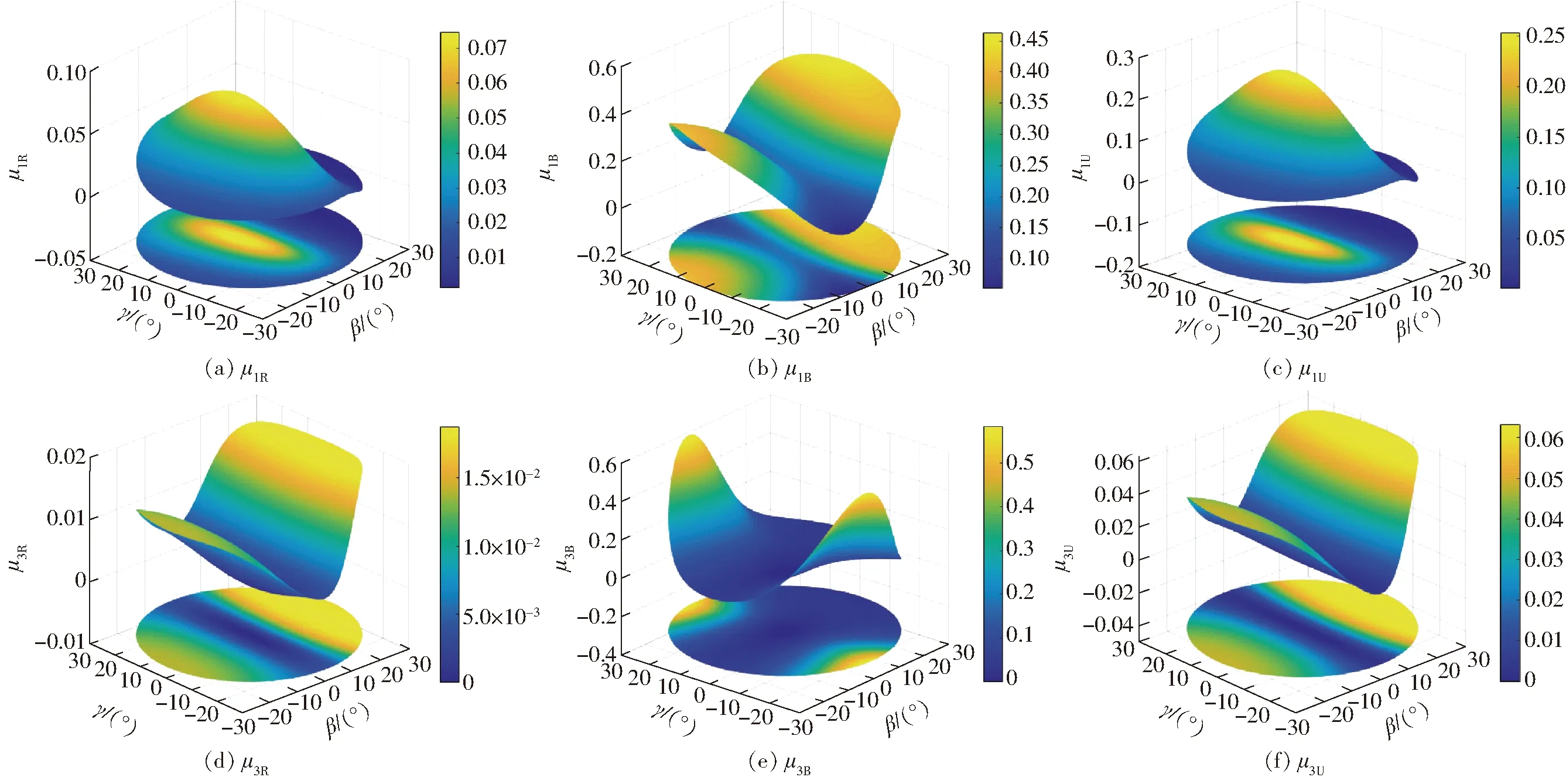
图8 P=P1时μ在平面z=-600 mm的分布

首先，施加外部载荷P=P1=(0, 0, 1 N, 0, 0, 0)，机构总应变能和局部应变能因子指标在规则工作空间的分布如图6、7所示。由于对称性，此处仅考虑了第1个UPR分支的应变能因子指标的分布。μiR、μiB和μiU分别表示第i分支的R铰、杆件和U铰的应变能因子指标，由图6、7可以看出，总应变能U和局部应变能因子指标μ均关于γ=0对称，这与机构的结构分布吻合，并且当给机构施加一个竖向力时，应变能最小即刚度性能最优的位置在初始位置。值得注意的是，UPR分支杆件的μij最大值为0.45，RPU分支杆件的μ最大值为0.5；UPR分支和RPU分支R铰的μij最大值分别为0.08和0.02；UPR分支和RPU分支U铰的μij最大值分别为0.25和0.07。相同的R铰在不同的分支中其μij分布不尽相同。由图6、7可以看出，在竖向力的作用下，2UPR-RPU并联机构样机各元件所存储的应变能从大到小依次为杆件、UPR分支中的U铰和R铰，即合理地提高杆件的刚度性能，如增大杆件的横截面积或选择刚度性能更好的材料，可以更有效地提高机构的刚度性能；UPR分支U铰的μ最大值达到0.25，说明此处U铰设计不合理，合理地改善U铰的设计提高其刚度性能也是改善机构刚度性能的一个有效途径。图8给出了μij在平面z=-600 mm的分布，由图8可以看出，μij与机构的姿态密切相关。以上分析可知，机构的刚度性能不仅与铰链本身的刚度性能有关，还与铰链位置以及机构姿态有关。

为了研究外部载荷对全局应变能因子指标的影响，表 2给出了在不同外部载荷作用下应变能因子指标在规则工作空间中的平均值。如果P=P1，则应变能主要存储在UPR分支的U铰链和杆件中，其占总应变能的80%。RPU分支杆件的全局应变能因子指标仅为0.08，表明当沿着Z轴的力作用在移动平台上时，第3个杆存储较小的应变能。也就是说第3个杆件对机构的刚度性能影响较小。当P=P2=(0.8 N，0.3 N，0.52 N，0，0，0)时，应变能主要储存在第3杆中，占总应变能的82.5%。在这种情况下，增加第3杆的截面面积可以更有效地提高机构的刚度性能。与其他弹性元件相比，UPR分支中R铰和U铰中存储的应变能可以忽略。第3分支铰链储存的应变能仅占1.51%。并且由于外部载荷的不对称，两个UPR分支中存储的应变能也不再相同。图9给出了指定工作空间中3根杆件的全局应变能指标的分布图。当P=P3=(0.52 N，0.3 N，0.8 N，0.5 N·m，0.7 N·m，0.51 N·m)时，第3杆储存的应变能占55.0%，第1杆和第2杆储存的应变能占41.0%。因为第3杆件此时具有较大的应变能量，给其设计较大的横截面面积是合理的。由于篇幅的限制，图10仅给出了3根杆的应变能因子指标分布。以上分析结果可知，关节对机构刚度性能的影响也与外部载荷的方向有关。

表2 弹性元件在不同载荷作用下的全局应变能因子指标

图9 P=P2时3个杆件的应变能指标分布图

图10 P=P3时3个杆件的应变能指标分布图

5 结论

(1)以2UPR-RPU过约束并联机构为研究对象，基于螺旋理论得出分支施加给动平台的驱动力和约束反力，基于材料力学和空间力系平移定理得到杆件和关节存储的应变能，利用应变能方法和卡氏第二定理得到形式紧凑的分支刚度矩阵，结合虚功原理和动平台平衡方程得到整体刚度矩阵的解析表达式，并同时得到驱动力和约束反力的解析表达式。与有限元模型计算结果的对比发现，误差不超过7.8%，验证了本文理论模型的正确性。

(2)为了研究2UPR-RPU并联机构各弹性元件对机构刚度性能的贡献，定义了应变能因子指标，给出了其在规则工作空间的四维切片分布图像，结果表明，弹性元件对机构刚度性能的贡献不仅与弹性元件本身有关，而且与弹性元件的排列、机构的姿态以及外部载荷的方向有关；在机构的刚度性能评估中，关节的柔度不可忽略。应变能因子指标从应变能的角度定量评价了各弹性元件对机构刚度性能的影响程度，具有明确的物理意义。