纯电动汽车动力电池降温性能研究

张凤麒

(厦门金龙旅行车有限公司， 福建 厦门 361006)

有关研究表明[1-3]：低温环境对锂离子动力电池性能的影响很大，通过改变电池材料体系来解决难度较大，并且基于当前环境下的材料供应链、设备、制造工艺及成本等方面考虑，也无法实现批量生产。因而目前广泛采用辅助加热系统[4-7]对电池进行加热，使其工作于最佳性能状态。

为了更清楚地了解电池在低温下的性能和特性，以便更好地优化纯电动汽车动力电池系统的加热策略和传热[8-9]、导热结构设计，本文选用磷酸铁锂电池包为研究对象，分别在0 ℃、-10 ℃、-20 ℃环境条件下测试单体电池降温与时间的关系，并结合风速对电池降温速率的影响建立电池降温速率计算模型。通过测试验证，电池降温数学模型能很好地反映电池降温特性。

1 电池降温性能测试

电池包放入环境舱之前，先静置于常温24 ℃±2 ℃环境下，直到电池温度趋于稳定(与环境温度差不超过2 ℃，静置时间不超过24 h)，然后将电池包置于0 ℃、-10 ℃、-20 ℃环境舱中分别静置24 h，记录3种测试环境温度下的降温数据与静置时间的关系，其中环境舱温度为0 ℃和-20 ℃的电池包中各单体电池的降温曲线如图1所示。

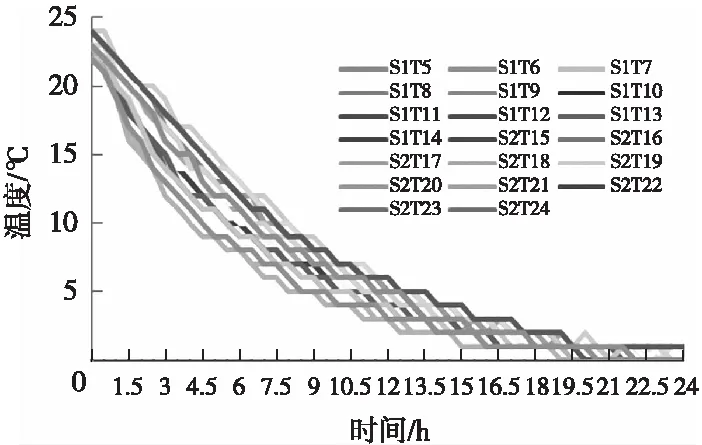
(a)环境温度0 ℃时

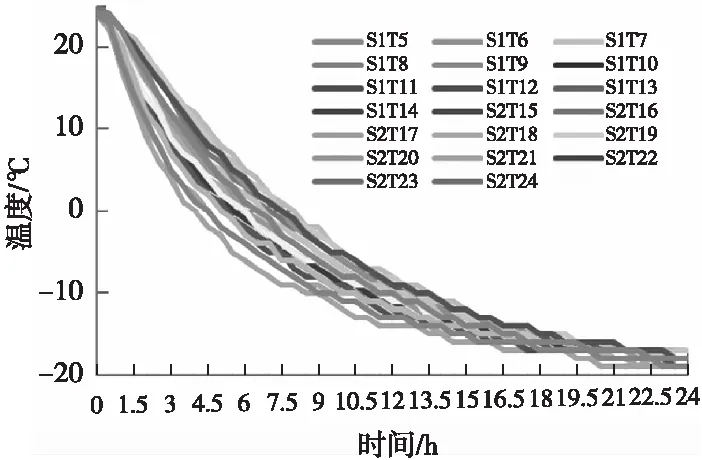
(b)环境温度-20 ℃时

首先在同一环境温度下进行横向分析。由图1可知，对于环境舱温度为0 ℃的环境，电池静置的前0.5 h，电池还未产生温降，体现出电池具有保持原温度状态的“惯性”。经过0.5 h的热传递，电池开始大幅降温，并且随着电池布置空间位置的不同而呈现不同的降温速率。在2～10 h静置时间段，各电池温度均以较大降温速率下降，在静置10 h后随着电池温度与环境温差的减小，降温速率不断降低。19 h后电池温度趋近于环境舱温度，基本达到平衡状态。对于环境舱温度为-10 ℃(未图示)和-20 ℃的环境，在0.5～9 h时，环境温度越低电池降温曲线越陡，在静置9 h以后，降温曲线缓慢下降。总体上有类似的降温过程。

从纵向分析，3种环境温度下降温曲线的上下极限线所形成的带宽基本一致，只是降温速率随着环境温度的下降而增大。上下极限线之间的带宽和电池包的宽度有关系，越靠近电池包中部的电池散热条件越差，电池的降温速率越小，电池间的温差越大。本文选择的电池包宽度为830 mm，目前整车厂使用的电池包一般布置于舱内、底盘纵梁内，允许布置电池箱体的宽度一般不会超过该数值(根据标准GB/T 34013—2017[10]中除序号5推荐的尺寸大于该值外，其他均小于830 mm)，因此本方案数据具有一定的代表意义。从数据中还发现，电池间的温差会随着环境温度的降低而增大，在-20 ℃环境下电池间的最大温差达到了12 ℃。

2 电池降温速率数学模型的建立

为了更好地分析电池降温与环境温度的关系，对测量数据进行整理，提取出电池包中所有单体电池的温差与时间的对应数据，算出该电池包中电池平均温差与时间的一般关系，并以此建立电池降温速率数学模型(拟合曲线)，如图2(a)所示。

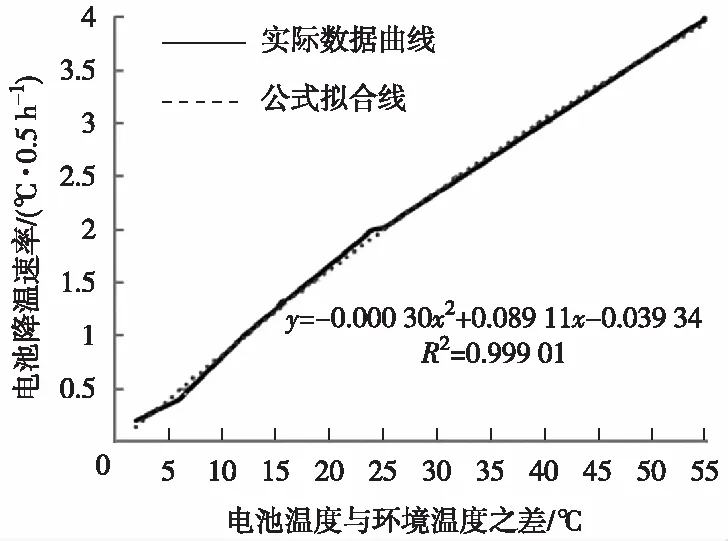
(a)拟合曲线

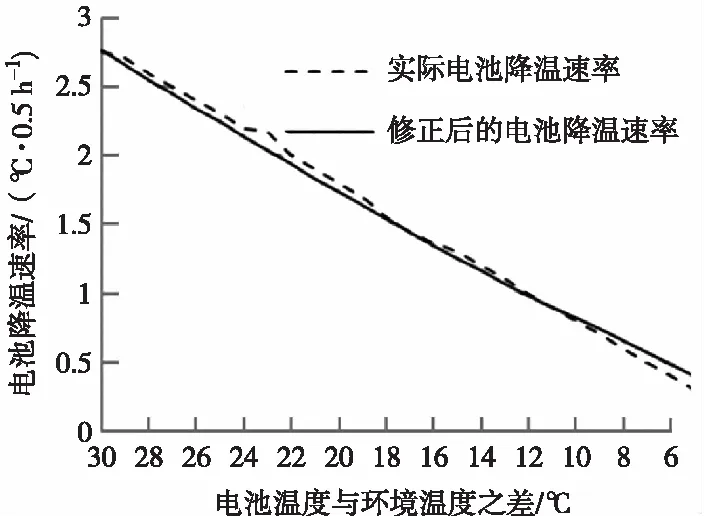
(b)对比图

该拟合曲线得R2=0.999，说明拟合曲线与实际数据之间具有极高的吻合程度，也说明拟合曲线具有良好的可靠性。从曲线可知，在温差达到32 ℃以上时，电池的降温速率≥5 ℃/h；在温差达到12～32 ℃时，电池的降温速率为2～5 ℃/h；温差低于5 ℃时，电池降温速率很小。

电池包实际安装于整车上，容易受到风速的影响。电池降温速率与风速成近似正比关系，因此引入线性修正函数，其数值具有随着电池温度与环境温度差值增大而增大的特性，适用于2 m/s≤风速≤8 m/s、温差>12 ℃时的环境条件。然而风速<2 m/s、温差≤12 ℃的环境条件，对电池降温速率影响很小，不需要引入修正函数。

定义φ(xs,xbt)表示电池降温速率(℃/h)，f(xs,xbt)表示测试降温速率，g(xs,xbt)表示环境修正函数，xs表示环境温度(℃)，xbt表示某时刻电池温度自变量(℃)，则电池降温速率数学模型可变为：

f(xs,xbt)=-0.000 3(xbt-xs)2+0.089 1(xbt-xs)-0.039 3

(1)

g(xs,xbt)=0.01(xbt-xs)2+0.087,and(xbt-xs)≥12

(2)

(3)

3 数学模型的测试验证

电池包安装于整车上，在内蒙进行降温测试，环境温度为-9～-15 ℃，风速为2～5 m/s时，实际单体电池降温速率曲线与按本文数学模型计算所得的单体电池降温速率曲线对比如图2(b)所示。从数据中可知，计算数据具有较好的吻合度，对于实际评价降温时间和加热策略的设计具有较好的参考价值。

为了进一步验证电池降温速率数学模型的准确性，本文多次测试电池包加热数据，如图3所示，计算涉及的基本参数见表1。图3中，测试开始至时间8:30，电池处于升温状态，8:30以后有7个完整的降温和升温循环。随机抽取降温和升温阶段数据来验证数学模型的准确性，即通过数学模型来计算降温数值，然后通过热平衡方程计算单体电池总体上的降温(或升温)数值，并与单体电池最低温度曲线数据(最高值和最低值边界线)对比一致性(注：电池包启动加热策略以单体电池最低温度作为关键指标)。

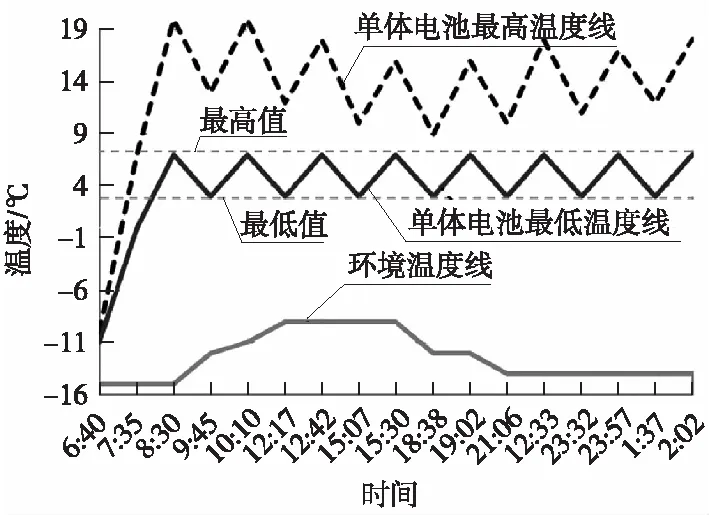
图3 电池包加热测试数据

表1 电池升降温计算涉及的基本参数

为了验证升/降温模型，建立热平衡方程，单体电池最终升高或降低的温度值Tdc为：

Tdc=Tj-Ts+ΔT

(4)

其中加热温度Tj=Vj×Tt。

散热温度Ts的求解利用牛顿-柯特斯(Newton-Cotes)公式：

(5)

式中：f(xk)为每个温差点下的降温速率；Tt-av为单位温度等分总时间。

电池充放电引起的温度变化ΔT，利用焦耳定律(纯电阻电路)和比热容公式：

Q=I2Rt=Cm(Te-Ts)

(6)

由式(6)推导计算：

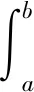
(7)

首先分析升温阶段数据：第1个升温阶段数据分析，时间9：45至10：10，环境温度由-12 ℃上升至-11 ℃(图3曲线)，单体电池温度由3 ℃上升至8 ℃(图3曲线)，则温差由15 ℃上升至19 ℃，利用本文电池降温速率数学模型计算可得降温速率,见表2，依式(4)～式(7)求解得到单体电池自然降温值Ts=1.24 ℃，理论加热升温值Tj=5.25 ℃，单体电池放电升温值ΔT=0.003 ℃(Q=348.6 W)，可求得单体电池最终升温值Tdc=5.25-1.24+0.003≈4.01 ℃，而实际升温测量值为4 ℃，计算结果与实际测试数据是一致的。

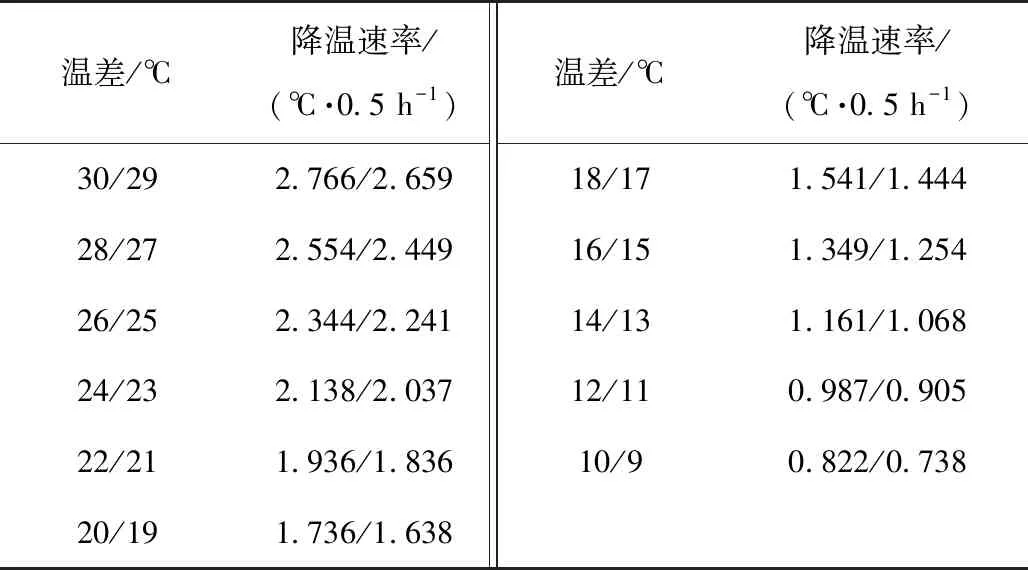
表2 不同温差条件下电池降温速率

取第2个升温阶段数据分析，经同样计算，可得单体电池最终升温值Tdc=5.25-1.01+0.002 8≈4.24 ℃，而实际升温测量值Tdc=4 ℃。计算结果与实际测量数据吻合较好，后续的几个升温循环，用本文数学模型计算降温数据均与实际测量数据吻合良好。

分析降温阶段数据：第1个降温循环数据时间8：30至9：45，环境温度由-15 ℃上升至-12 ℃，单体电池温度由8 ℃下降至3 ℃，则温差由22 ℃下降至15 ℃，利用电池降温速率模型计算式可得降温速率，见表2，依式(4)～式(7)求解得到单体电池自然降温值Ts=4.1 ℃，单体电池充电升温值ΔT=0.202 ℃(Q=23 461 W)，可计算得单体电池最终降温值Tdc=4.1-0.202≈3.9 ℃，而实际降温值为4 ℃，单体电池降温数据计算值与实际值基本吻合。

此外，从测试数据中得出电池包的一个降温特性：即在测试的前0.5 h左右，电池具有保持原温度的惯性，下降温度会很小，有种阻碍温度下降的“作用力”。然而，在温度较低时，电池又会保持原降温速率的惯性，持续原降温特性继续降温0.5～1 h。

在测试中还发现，随着环境温度的降低，电池包总加热时间成正比增加，基本遵循环境温度每降10 ℃，电池包加热至同一单体最低温度位置所需时间近乎成倍增加的规律，同时电池温差在逐渐增大，如图4所示。

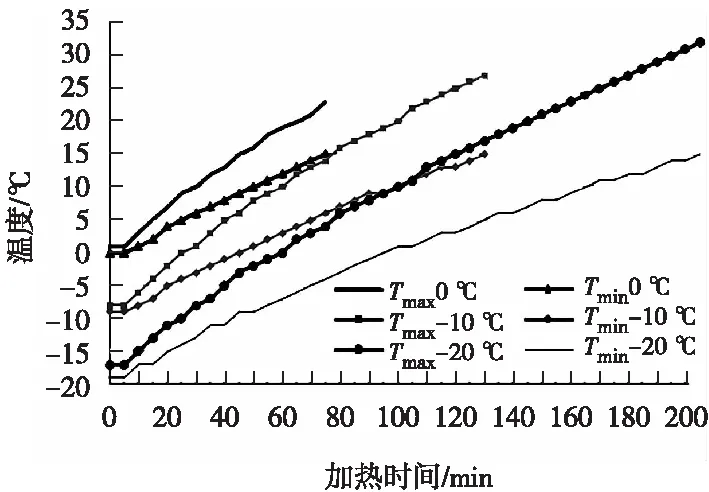
图4 电池包加热时间与环境温度关系图

4 结 论

本文根据环境舱测试数据建立磷酸铁锂电池降温速率计算模型，结合实际环境条件来修正模型(存在风速和温差影响的情况下)，然后运用模型计算电池降温数据，与整车实际测试数据对比一致。此外，本文测试选用的电池箱体长宽高尺寸为1 200 mm ×830 mm×280 mm，该尺寸基本可以涵盖目前客车标准箱、轻客车型和商用车型所用大部分电池箱尺寸，因此其在反映静态降温特性方面具有较好的实用性和可靠性。