基于混合整数规划模型的星树型油气管网布局整体优化研究*

周 军 周柳玲 梁光川 陈 川 李泽龙 黄薪宇 周 轩

(1. 西南石油大学石油与天然气工程学院 四川成都 610500； 2. 中国石油塔里木油田公司 新疆库尔勒 841000)

油气集输系统将油气原料进行收集、处理和输送，是油田建设工程的重要组成部分。油气集输系统非常复杂，建设投资占据油气田开发成本比例较大。因此，对油气集输管网整体优化设计及建设合理的管网布局，既是降低油气田开发成本的手段，也是油气田建设中最棘手的问题之一。

确定管网连接结构是优化管网布局的基础，不同的连接结构将直接影响油气集输管网的拓扑布局优化。很多学者对集输管网的布局优化模型进行了研究。Wang 等[1]建立了海底丛式管网拓扑优化数学模型，提出了基于超链接矩阵的启发式算法；Wang 等[2]以投资费用最小为目标函数建立数学模型，并提出利用分步优化的方法求解，但模型仅局限于管网的平面结构；Zhang 等[3-4]以常见的星状管网、树状管网拓扑为研究对象，将集输半径、经济流量等考虑进海上集输管网的优化中，建立了混合整数线性规划模型并求解，但不能适用于复合型管网；Zhou等[5]考虑集输半径、处理规模以及连接井口数量等约束，针对陆上星树型油气田管网提出了数学模型，该模型将相关设施位置考虑为离散型以符合油气田建设实际情况，但仍采用分级策略求解，且优化出的集输方案不是全局最优解。

油田集输管道系统优化包含最优井组划分、点集几何中心点[6]、图论最小生成树[7]、最短路径[8-9]和许多其他子问题，这些子问题大部分是典型的不确定多项式困难问题[10]。目前，集输管网的拓扑结构优化一般采用分步优化的方式求解[11]。然而，分级优化得出的管网布局是由各子问题的最优解组成的一种综合方案，是一种局部最优解,而不是整体优化管网得到的最优解。

综上所述，现有的模型和优化方法不能解决星树型管网复杂的连接问题，也没有获得其全局最优的结果。本文关注油气集输管网的布局优化设计，主要以集输站费用和管线费用为影响集输管网布局的主要因素，考虑影响分离效果的限制条件，包括集输站处理容量、集输半径和数量限制约束，提出了一个通用的混合整数规划模型，将井组划分、中心点位置、最小生成树等子问题同时优化，得到油气集输管网的最优拓扑形态、集输站位置、海上浮式生产储油船位置及相应的集输方案的各部分投资。

1 数学模型

1.1 优化目标函数

以平台投资和管线投资组成的管网投资最小为目标函数，定义星树型管网的两级结构：井至下一级集输站点为一级管网，其间的管线为一级管线；下一级集输站点间为二级管网，其间的管线为二级管线。

minf=fpg+fgg+fg+fc

(1)

其中

(2)

(3)

(4)

(5)

式(1)～(5)中：f为总投资，元；fpg为井至集输站间一级管道投资，元；fgg为集输站间二级管道投资，元；fg为集输站投资，元；fc为中央处理厂投资，元；Aij为井i至站j间一级管线单位长度价格，元/m；Bjk为站j至站k间二级管线的单位长度价格，元/m；Cj为一个集输站价格，元；Ps为一个中央处理厂价格，元；Dij为井i至站j间的距离，m；Djk为站j至站k间的距离，m；σij为0或1的变量，当且仅当井i∈I连接到集输站j∈J时，σij为1，否则为0；θjk为0或1的变量，当且仅当集输站j∈J与集输站连接时，θjk为1，否则为0；uj为0或1的变量，当且仅当集输站j∈J时，uj为1，否则为0；es为0或1的变量，当且仅当中央处理厂s∈J时，es为1，否则为0；I为模型中井口编号的集合；J为模型中待选集输站的集合;m和n分别代表生产井和集输站的数量。

1.2 约束条件

1) 隶属关系约束。每个井只隶属于一个集输站，表示为

(6)

2) 集输半径约束。油气通过一级管线从井口平台输送到中心平台，在输送过程中，管道中的流体与管壁的摩擦导致沿线压力下降。为了保证流体能在要求的压力下输送，一级管线的设计长度必须小于允许的最大管线长度Lmax，表示为

σijDij≤Lmax(∀i∈I，∀j∈J)

(7)

3) 处理容量约束。中心平台内的分离器等设备，只有在合适的容量范围才能有最好的分离效果。为了保证产量分配平衡，各集输站的处理容量均不超过最大值Qmax，表示为

(8)

式(8)中：wi是第i口井的容量；Qmax是集输站的最大处理容量。

4) 连接到集输站井数量约束。每个集输站连接的井口数不能超过最大值Mmax，表示为

(9)

5) 连接关系约束。只有集输站j存在时，井口i才能连接到该集输站，表示为式(10)；如果集输站j和集输站k相连接，那集输站j和集输站k必定存在，表示为式(11)。

σij≤uj(∀i∈I,∀j∈J)

(10)

(11)

6) 上层枝状布局约束。树状结构较为复杂，需要同时考虑以下2个约束条件：集输站的总个数比二级管线的数量少1，这样可以防止二层拓扑结构为星状，表示为式(12)；同样也需要防止生成环状拓扑结构，表示为式(13)[11]。

(12)

(13)

式(12)～(13)中：H是N的真子集；l是H中的一个集输站。

7) 中央处理厂数量约束。星树型集输管网只有一个中央处理厂，表示为

(14)

2 求解算法及步骤

针对本文提出的星树型数学模型是混合整数规划模型，采用分支定界法来整体求解。分支定界法是一种求解整数规划问题的最常用算法，通过快速不断地搜索松弛问题最优解来缩小范围。设定优化问题为F，通过对优化问题的所有可行解空间进行搜索，最后得到最优解为Fopt，其求解步骤如下：

1) 令活点集合={F}，上界Fu=+∞，定义当前最好的整数解Φ；

2) 如果活点集合=Φ,则转向第7步，否则，选择一个分枝点k∈活节点，从活点集合中去掉点k；

3) 求解点k对应的松弛问题LFk，若此问题无解，转回第2步；

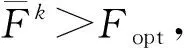
6) 如果k对应的松弛问题LFk的最优解zk不满足整数要求，按zk某个非整数分量生成点k的2个后代点，令这2个后代点为活点，并加入到活点集合中，转回第2步；

7) 如果当前最好的整数解为Φ,Fu=+∞,则原问题无解，否则，当前最好的整数解就是原问题的最优解，Fopt就是最优值，计算停止。

3 算例分析

3.1 单个约束影响

一般来说，优化管网时需要考虑的布局参数包括设施数量、位置、管道长度、处理容量等，每个部分的成本不同。若集输站投资过大，则只能减少集输站的数量以降低集输站投资，但是可能导致部分集输站超过最大处理容量，或导致井至集输站的管道长度超过集输半径的限制。为了具体分析各参数的变化对整体布局形态和各部分投资的影响，以一个区域面积1 000 m×1 000 m、单井产量8 000～9 000 m3/d的虚拟陆上气田为例，对包含处理流量、集输半径和集输站数量的星树管网整体模型进行算例分析。在特定的管径条件下，本文设定一级管线的单位长度价格为596.4元/m，二级管线的单位长度价格为779.4元/m，集输站价格为1 022.31×104元，中央处理厂的价格为1.9×108元。

整体优化后的星树管网具有了三重约束，分别为：容量约束Qmax0=8×104m3/d 、半径约束Lmax0=400 m、数量约束Mmax0=8，其最优布局图如图1a所示。该集输方案在12、16、17和25共建了4个集输站，每个集输站连接的井数相同，即分配给每个集输站的流量合理，管网布局均衡。对于具有三重约束的管网来说，改变任意一个约束条件都可能会使管网的拓扑形态以及投资发生变化。因此，为了分析单个约束的改变对具有三重约束星树管网布局的影响，对基础数据做以下处理进行整体优化：①设置Qmax0=8×104m3/d，Lmax0=400 m，增加数量约束Mmax1=6和Mmax2=10；②设置Mmax0=8和Qmax0=8×104m3/d，增加半径约束Lmax1=300 m和Lmax2=500；③设置Lmax0=400 m和Mmax0=8，增加Qmax1=6×104m3/d和Qmax2=10×104m3/d，图1b～d为其中3组三重约束整体优化管网布局。全部7组三重约束整体优化最优布局方案的集输站最优位置、一级管线投资、二级管线投资、集输站投资及总投资如表1所示。可以看出，当固定任意2个约束并改变第3个约束条件时，大多数星树管网方案的集输站数量、集输站位置以及各部分的投资费用都会变化，如果第3个约束的数值减小，则集输站的数量增多，总投资增大。

然而从表1可以看出，当Lmax0=400 m、Mmax0=8时，Qmax0=8×104m3/d和Qmax2=10×104m3/d的星树管网在整体优化下，所得方案的集输站数量、所在生产井位置，以及各部分投资均相同，因此可以认为这2种方案的布局形态完全一样，说明当容量约束超过某个特定数值时，管网布局不会再受到集输站处理规模的影响，集输半径约束或数量约束开始成为主导因素。同时可以发现，约束的差异使得集输站位置和管网结构差异明显，且优化出的星树管网布局形态为下层为星状、上层为树状的2层拓扑结构(图1)，验证了本文的星树管网模型的正确性和可靠性。

表1 不同约束条件下整体优化管网投资

3.2 分级优化与整体优化对比

整体优化可以由分级优化拼凑得到，但这种方法得到的整体优化并不是全局最优解，而是各子问题的最优解。因此，这里将运用整体优化方法[1]求解星树管网的整体布局。

采用表1中的7组数据，对模型采用分级优化策略进行求解，得到的各项投资如表2所示。这里以Qmax0=8×104m3/d、Lmax0=400 m、Mmax0=8的三级约束为例进行分析。由于整体优化和分级优化的三级约束相同，因而2种优化方式下的井组数量和集输站数量也相同，但服务的井口却不完全相同(图2)：分级优化策略下划分到井组G1的生产井与整体优化下划分到井组G1*的生产井完全相同；但分级策略将整体优化下隶属于井组G4*的8号井划分到了井组G2，将整体优化下隶属于井组G3*的1号井划分到了井组G4。由于井组划分结果直接影响集输站的位置、一级管线和二级管线的长度，进而影响管道投资，因此两种优化方案的投资也不相同：分级优化的总投资为23 538.68×104元，而整体优化的总投资为23 534.95×104元。整体优化总投资以全局管网投资最小为目标，得到了全局最优解，因此得到的总投资较小。

表2 不同约束条件下分级优化管网投资

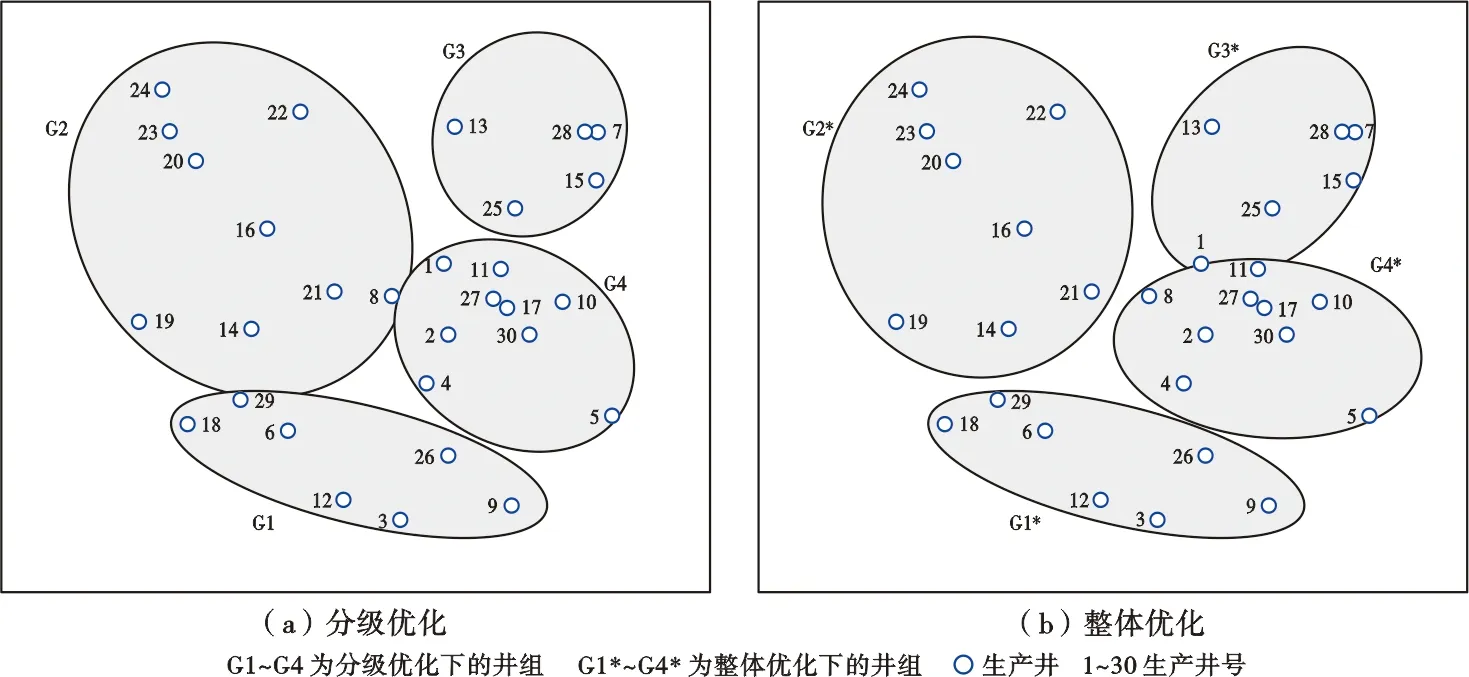
图2 星树管网分级优化和整体优化的布局结果(Qmax0=8×104m3/d，Lmax0=400 m， Mmax0=8)

整体优化与分级优化的一级和二级管线投资优化率(投资减少部分与原投资的比值)相比(表3)，一级管线的投资增加，二级管线的投资降低(最大的优化率达到36.95%)。这是因为分级优化的子问题井组划分一般以一级管线为最小目标函数，使得分级优化一级管线投资一般比整体优化低；但分级优化将一级管线投资与二级管线投资分别求解，造成其二级管线投资一般高于整体优化。因此，整体优化较分级优化能进一步降低管网投资。

表3 星树管网整体优化与分级优化的投资优化率

4 实例分析

1) 某陆上油田。

某陆上油田面积5 km×5 km，包括49口油井且井口分布相对集中。油田采用井—集输站—中央处理厂的二级布站方式将油井划分为6个井组，建立了6个集输站，集输系统采用星树型管网布局。设置该油田单个集输站价格550.4×104元，一级管道管径76 mm，管线单位长度价格78.6元/m，二级管道管径114 mm，管线单位长度价格为140.9元/m，处理容量约束。容量、半径和数量约束分别为80 000 m3/d、1 400 m和10，采用该油田的数据对模型整体优化求解并将整体优化下星树管网布局与原管网布局进行比较，结果如图3所示。可以看出，整体优化的集输站在W4、W7、W14、W16、W33和W49井上建立，中央处理厂设置在S4上。与原方案相比，整体优化得到的6个井组与原方案划分的井组类似，且井组内井站间连接方式为星状结构、站间的连接方式为树状结构，证明了该模型的正确性和可靠性。

图3 某陆上油田管网现有布局与整体优化布局对比

2) 某海上油田。

某海上油田面积15 km×15 km，工程模式为“全海式”，将井组位置作为中心平台和海上浮式生产储油船的候选位置。设置该海上油田单个井口平台价格33 400×104元，一级管道管径150 mm，管线单价为8 600元/m，二级管道管径200 mm，管线单价为9 500元/m，处理容量约束，容量、半径和数量约束分别为5 000 m3/d、6 000 m和3。在给定星树型拓扑结构基础上，对具有处理容量、半径和数量约束的管网进行整体优化，结果如图4所示。该布局共有5个中心平台和9个井口平台，一级管线总长16.54 km，二级管线13.49 km，海上浮式生产储油船在中心平台P3附近。该管网投资中心平台和井口平台投资分别为442 000×104元和300 600×104元，最小总投资为769 639×104元。可以看出，各井口平台以星状形态将产液输送到中心平台，中心平台以枝状的结构将产液汇集到海上浮式生产储油船。该海上集输方案符合“全海式”工程模式，满足管网中心平台的三重约束条件，证明了该模型的适用性。

图4 某海上油田管网整体优化布局

5 结论

1) 本文提出的星树型油气管网数学优化模型是一种混合整数规划模型，考虑了处理容量、集输半径和数量约束条件，通过整体优化得到了全局最优拓扑、最佳设施位置，以及对应的集输方案的各部分投资。

2) 以陆上虚拟气田为例对模型整体求解，认为在不同约束条件下，优化得到的星树管网布局方案及各参数变化对整体布局形态及各部分投资均有一定影响。某陆上、海上油田的实例分析表明，在相同的集输半径约束、处理容量约束和数量约束条件下，整体优化比分级优化的管网投资更低。