基于新型冠状病毒传播的数学模型研究*

付吉丽,黄立强,王玉文

(1.哈尔滨石油学院；2.哈尔滨师范大学)

0 引言

新型冠状病毒(COVID-2019)自2019年12月爆发以来,已蔓延至全球,严重影响了世界各国人民的身体健康和生命安全.它的出现引起了人们的极大关注，它的传播速度快，传播范围广，对全球都产生了很大的威胁，对各国的经济、人民的生活、生命财产造成了巨大影响.为了弄清新型冠状病毒疫情发展的特点和规律，对于世界范围内的疫情发展能够有一个清晰的认识.该文主要分析了各国疫情情况，并且提出了相应的建议.通过已有的基本数据建立SEIR数学模型，并结合建立好的SEIR模型进行分析思考，再对主要的疫情国家进行管控效果进行综合评价.

1 数据分析结果

图1 主要国家感染人数统计图

接着通过所统计的128天数据，计算出各个国家增长人数的平均数.接着通过所统计的128 d数据，计算出各个国家增长人数的平均数.求得美国12765.7人/d，德国140.3人/d，俄罗斯2896人/d，西班牙1848.7人/d，英国2072.1人/d，中国648.4人/d.从得出的数据进行比对来看美国增长速率依然最快，俄罗斯第二，之后依次是英国、西班牙、德国和中国.其中、德、英、西四个国家趋于平稳.

通过死亡人数折线统计图图2来看美国依旧是死亡人数最大的国家，其次是英国接下分别是西班牙、德国、中国和俄罗斯.然后通过计算出所选取的主要国家的死亡率，进行死亡率排列.其中美国死亡率为5.97%，英国死亡率为13.90%，西班牙死亡率为12.30%，德国死亡率为4.70%，中国死亡率为5.58%，俄罗斯死亡率为1.10% .

图2 主要国家死亡人数统计图

综上所述，通过图3～图8增长速率、感染人数平均数、死亡数、每日新增确诊数将国家分为高风险国家、中等风险国家和低风险国家.

图3 中国日确诊人数趋势图

图4 美国日确诊人数趋势图

图5 英国日确诊人数趋势图

图6 俄罗斯日确诊人数趋势图

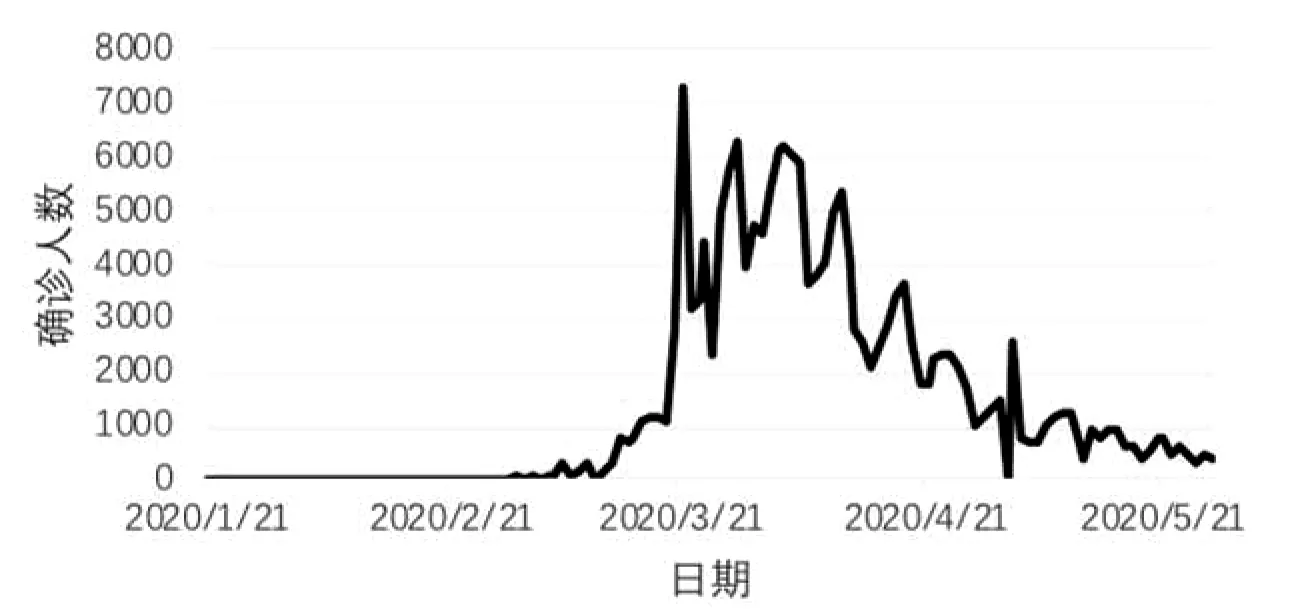
图7 德国日确诊人数趋势图

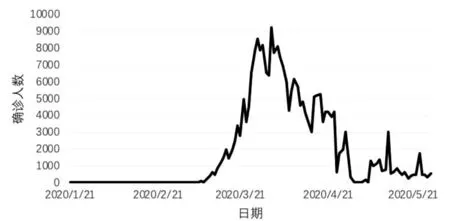
图8 西班牙日确诊人数趋势图

对所选取的六个国家针对疫情管控方面进行客观、全面的评价，属于多目标决策问题.首先选择合理的指标，通过选择感染人数的增长速率、死亡率、每日新增确诊人数和感染总人数为所选参数指标.通过以中国为参考建立综合评判模型[1].

(1)确定因素集.记为：

U={增长速率u1,死亡率u2,每日新增确诊人数u3,感染总人数u4}

(2)确定评语集.对国家对疫情的管控情况，将其分为五类：防控优秀，防控良好，防控一般，防控较差，防控差.记为：V={防控效果优秀v1,防控效果良好v2,防控效果一般v3,防控效果较差v4,防控效果差v5}

(3)确定各因素的权重.记为：

A=[0.25,0.3,0.25,0.2]

(4)确定模糊综合判断矩阵.对指标u1的的评判有网友舆论来打分

R1=[0.75,0.2,0.05,0,0]

上式表示参与打分的网友中，有75%的人认为中国感染人数增长速率防控优秀，20%的人认为中国感染人数增长速率防控良好，5%的人认为中国感染人数增长速率防控一般，认为中国感染人数增长速率防控较差和差的人为0.用同样的方法对其他因素进行评价.

对指标u2和u3由组内成员去市内重点医院进行问卷调查，由医护人员来确定:

R2=[0.8,0.2,0,0,0];

R3=[0.7,0.2,0.1,0,0]

对指标u4由组内成员进行打分确定:

R4=[0.9,0.1,0,0,0]

以Ri为第i行构成评价矩阵

它是从因素集U到评语集的一个模糊关系矩阵.

(5)模糊综合评判.进行矩阵合成运算：

[0.785,0.18,0.0375,0,0]

取数值最大的评语作为综合评价结果，则中国评判结果为“防控效果优秀”.

对于其余5个国家采取上述过程进行综合评价.

(1)美国

[0,0,0.085,0.27,0.645]

取数值最大的评语作为综合评价结果，则美国评判结果为“防控效果差”.

(2)俄罗斯

[0.58,0.315,0.105,0,0]

取数值最大的评语作为综合评价结果，则俄罗斯评判结果为“防控效果优秀”.

(3)德国

[0.62,0.28,0.07,0.03,0]

取数值最大的评语作为综合评价结果，则德国评判结果为“防控效果优秀”.

(4)英国

[0.22,0.21,0.295,0.275,0]

取数值最大的评语作为综合评价结果，则英国评判结果为“防控效果一般”.

(5)西班牙

[0.2475,0.2225,0.31,0.22,0]

取数值最大的评语作为综合评价结果，则西班牙评判结果为“防控效果一般”.

2 模型的建立

假设1

(1)设未感染者、感染者、治愈者、死亡者所占比例分别为s(t),y(t),r(t),q(t),这里

s(t)+y(t)+r(t)+q(t)=1.

(2)设病人的日接触率为λ，即每个病人每天有效接触的平均人数，日治愈率为μ(治愈人数占病人总数的比例)，传染病死亡率为m，即死亡人数占病人总数的比例.

假设人群中总人数N不变，不考虑出生和自然死亡因素.

首先给时间t一个增量Δt，考虑在Δt内增加的病人数及减少的未感染者、治愈者及死亡者人数，则Δt内增加的病人数为

N[y(t+Δt-y(t)]=λNy(t)s(t)Δt-μNy(t)Δt-Nmy(t)Δt

(1)

Δt内减少的未感染者

N[s(t+Δt)-s(t)]=-λNy(t)s(t)Δt

(2)

Δt内减少的治愈者

N[r(t+Δt)-r(t)]=μNy(t)Δt

(3)

Δt内减少的死亡者

N[q(t+Δt)-q(t)]=Nmy(t)Δt

(4)

将式(1)～(4)两端除以Δt，消去N，取极限得

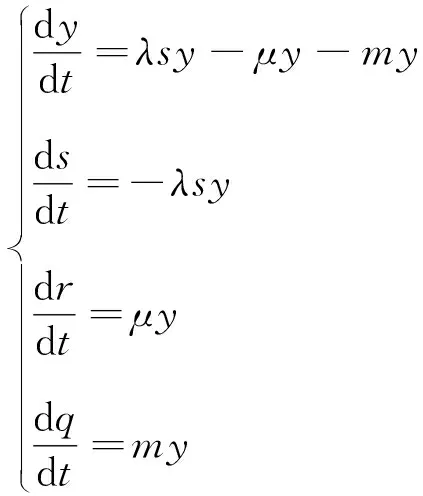
(5)

实证选取数据总人数N=60000000，以2020年5月27日国家卫健委官网发布的新冠肺炎数据作为未感染者比例r(t)、s(t)、感染者比例y(t) 、治愈者比例r(t)、治愈者比例r(t)的初始值，即s(0)，y(0)，r(0)，q(0) 分别为0.999976，0.000014，0.0000006，0.0000004.根据1月27日～5月26日国家卫健委官网发布的实际数据，可知1月27日～5月26日的平均治愈率为0.94318，平均死亡率为0.05584.由此赋值日治愈率μ=0.94318，死亡率m= 0.05584，预测天数t= 180 d.根据改进的SIR模型方程(5).

3 模型检验及评价

选取中国5月21日～5月25日5天的感染者人数，死亡人数和治愈人数.与表1所列数据变化与图3曲线进行比照.

表1

根据比较可以看出，预测数据相差不大，较为吻合.模糊综合评判方法可以避免凭经验进行目标选择所固有的主观性.使并购决策更加科学合理.SIR模型结构简单、可操作性强，适用于描述疾病发展的整体趋势[3-4].因疫情传播实际过程中日接触率、治愈率变化较快，且还有其他因素也在变化，因此改进的SIR模型相对来说还比较理想化，后续还需进一步改进.所选取的国家有较大的主观性，缺少更为客观的筛选模式.