一类具有B-D功能反应项的捕食系统的定性分析*
2020-03-07李畅通冯孝周
李畅通,冯孝周
(西安工业大学 理学院,西安 710021)
为了有效的控制害虫,农业部门和经济学家们提出了有害生物综合治理(Integrated Pest Management,IPM)策略。通常IPM 主要利用化学控制,生物控制和人工防治等互相配合的方式,建立高效的综合防治体系来控制害虫。其中生物控制主要是利用投放天敌、收获和抓捕等手段来控制害虫的数量,而化学控制是利用杀虫剂等化学物品来迅速大量的杀死害虫。在实施害虫控制时应该有效结合2种控制策略,相互配合,从而实现最优的控制策略。
近年来,具有害虫综合控制的捕食系统已经得到了广泛研究并得到了较好的结论[1-3]。然而很多文献将天敌的周期释放量定为一个不变的常数,这意味着农业资源对害虫的控制非常有效[4-8]。事实上,病虫害的爆发或再度猖獗往往具有突发性、不确定性等特点,所以害虫控制策略必定受到包括杀虫剂、天敌和人力等农业资源不足的严重影响,而这些影响往往是非线性的。具有非线性脉冲控制的模型比线性脉冲有更加丰富的动力学行为,也更切合实际[9-12]。然而具有B-D功能反应项的模型还鲜有研究,因此,本文研究了具有非线性脉冲控制的捕食系统
(1)
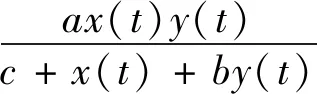
1 预备知识和基本引理
令R+=[0,+),在(nT,(n+1)T],n∈Z+上连续。令f=(f1,f2)T为系统(1)前两个方程的右端映射,显然f的光滑保证了解的存在唯一性。
引理1 令X(t)=(x(t),y(t))是系统(1)的一个解,如果初值X(0+)≥0,那么对于所有t≥0均有X(t)≥0成立。进一步,如果X(0+)>0,那么对于所有t≥0均有X(t)>0。
引理2 系统(1)的所有正解是一致最终有界。
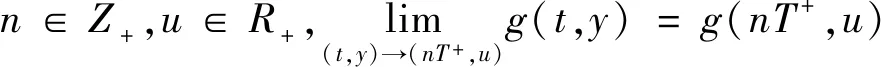
令脉冲微分方程
的最大解r(t)在[0,+)存在,则当t≥0且V(0+,x0)≤u0时,V(t,x)≤r(t)。
为了了解系统(1)害虫根除周期解的存在性,给出系统(1)的子系统的基本性质
(2)
根据文献[12]得如下引理
引理4 如果1-q2exp(-δT)>0,式(2)存在一个正的全局稳定的周期解为
t∈(nT,(n+1)T],n∈Z+。
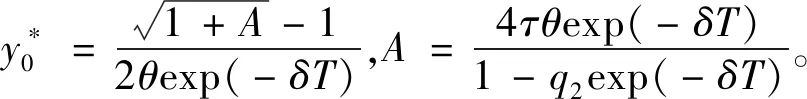
因此,系统(1)的害虫根除周期解为(0,y*(t))。害虫根除周期解的稳定性在分析系统的动力学行为和揭示生物意义方面起着关键作用,因此下文给出害虫根除周期解的稳定性的条件。
2 害虫根除周期解的稳定性
定理1 如果
则系统(1)的害虫根除周期解(0,y*(t))是局部渐近稳定的。
证明为了证明害虫根除周期解局部稳定性,令u(t)=x(t),v(t)=y(t)-y*(t),其中u(t),v(t)为小的扰动。令φ(t)为系统(1)的基解矩阵,因此φ(t)必须满足
其中φ(0)=E为单位矩阵。
系统(1)在脉冲时刻的方程为
定义矩阵
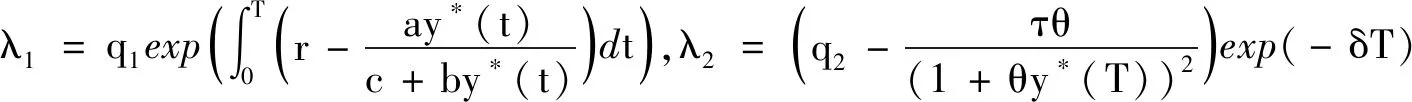
分析λ2的取值范围,因为0<1-q2exp(-δT)<1,则有

q2exp(-δT)<1,
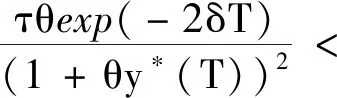
所以λ2>q2exp(-δT)-1>-1,即|λ2|<1。因此,当|λ1|<1时,害虫根除周期解(0,y*(t))是局部稳定的。因为
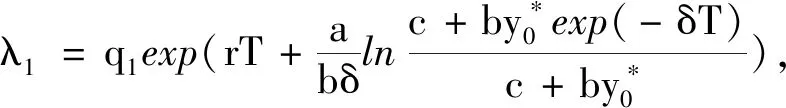
若害虫根除周期解失去稳定性,系统(1)的动力学行为将变得非常复杂。为此,令

且存在T0>0使得F(T0)=0。这意味着,当T
3 非平凡周期解当然存在性
利用文献[13]中的脉冲微分方程分支理论讨论系统(1)非平凡周期解的存在性,有如下主要结论:
定理2 若存在T0使F(T0)=0,当q2>τθ且Ka<4rbc时,系统(1)在T=T0发生超临界分支。
证明记Φ(t,X0)为具有初值条件X0=(x0,y0)的系统(1)的前两个方程的解,Φ=(Φ1,Φ2),ξ(t)=(y*(t),0)。定义映射

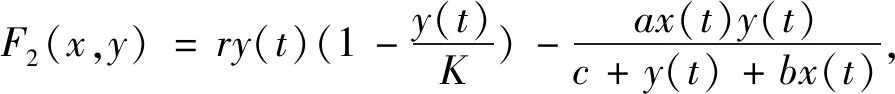
Θ2(x,y)=q1y(t)。
由文献[13]得
注意到


求二阶偏导数得
因此有
令

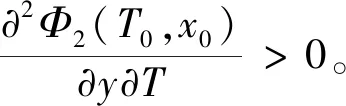
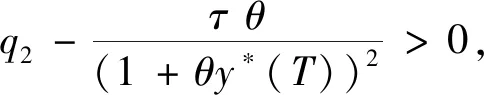

4 数值模拟
为了研究非线性脉冲如何影响系统(1)的动力学行为,通过分值参数图来反应某些特定参数对系统动力学行为的影响。当T>T0时,害虫根除周期解失去稳定性,此时系统变得相当复杂。为此,首先选取脉冲周期T作为分支参数,固定其他参数如图1所示,取参数r=2.69,K=2.4,a=1.1,b=0.001,c=1.05,d=0.22,β=0.91,q1=0.88,q2=0.96,τ=5.5。由图1可以观察到,系统动力学行为非常复杂,如出现倍周期分支、周期倍减分支、多吸引子共存和混沌等现象。当脉冲周期T由10增加25时,系统经历了3次倍周期分支以及周期减半分支。
特别的,当T=16时系统出现多吸引子共存现象,系统存在一个T周期解和2T周期解共存现象,如图2所示,系统(1)取T=16时的2个稳定的吸引子。当T由25开始增加,系统由稳定的T周期解分支出2T周期解,进一步倍周期分支导致混沌现象发生。当T接近31时,混沌消失系统出现一个8T周期解。随着T进一步增加,系统经历周期减半分支以及倍周期分支的动力学行为的转化过程,而倍周期分支最终又导致系统出现混沌现象。在混沌结束后,周期减半分支连续发生,当T=37.64时进入稳定的T周期解。
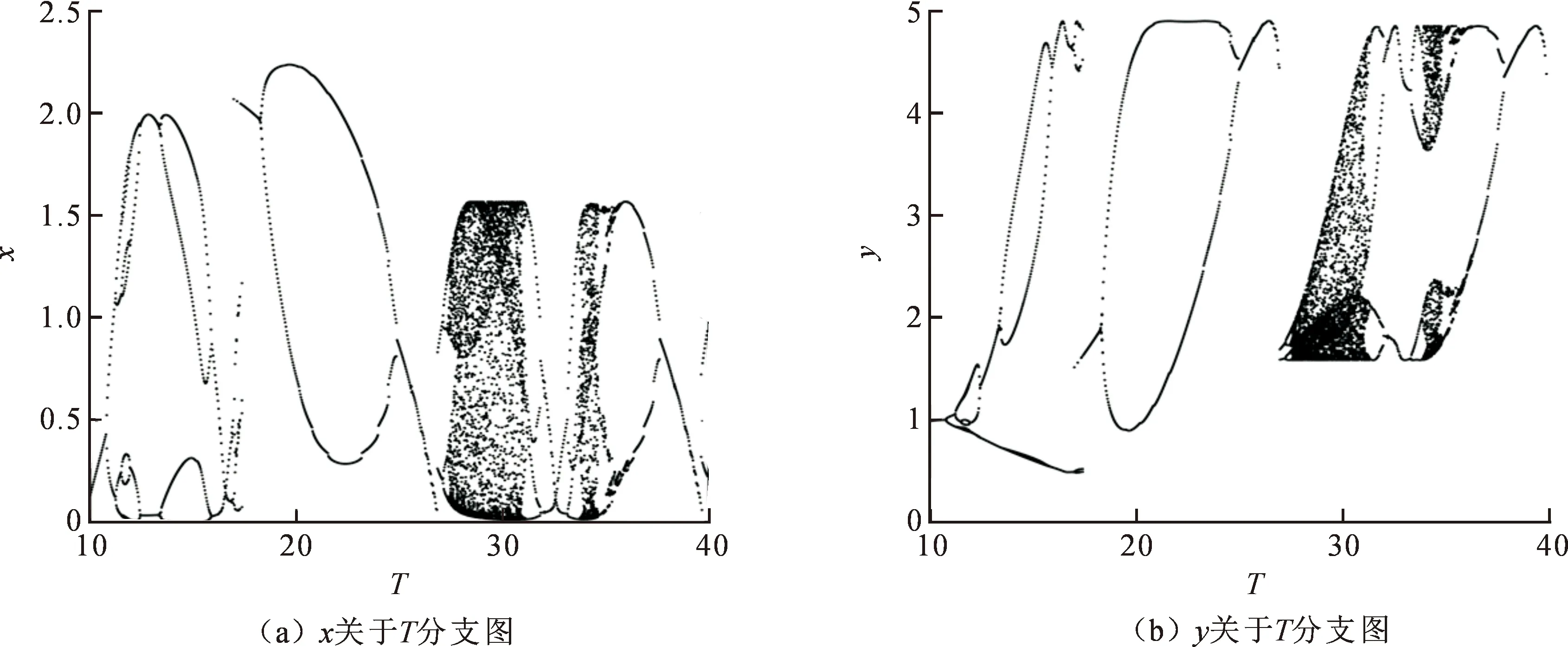
图1 脉冲周期T的分支参数图Fig.1 Bifurcation diagrams with respect to parameter T
图2为系统(1)的T周期和2T周期解共存现象。这意味着若选取不同的初值,系统的解最终稳定性会变化较大。固定参数如图1所示,若选取初值为(x0,y0)=(2,0.5),则系统(1)的解最终稳定为如图2(a)和2(b)所示;若选取初值为(x0,y0)=(2,1.5),则系统的解最终稳定为图2(d)和2(e)所示。这意味着害虫和天敌种群的最终稳定状态还依赖于它们的初始密度,二者的初始密度会影响害虫控制策略,在实际中,可以选取合适的初值,让系统稳定到预期的吸引子。
图3选取τ为分支参数图,当τ由2连续变到10时,可以看到参数τ对系统的动力学行为影响较大,如出现倍周期分支、周期减半分支、吸引子共存以及混沌现象。当τ=4.25时,系统有2个不同的2T周期解共存现象,图4给出2个共存的吸引子,图4(a)和4(b)选取初值为(x0,y0)=(2,0.5);选取初值为(x0,y0)=(2,3.5),系统的解最终稳定为如图4(d)和4(e)所示。

图2 关于图1的2个共存的吸引子Fig.2 Two coexistence stable attractors
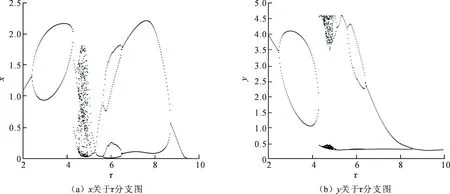
图3 最大投放天敌量τ的分支参数图Fig.3 Bifurcation diagrams with respect to parameter τ
数值模拟说明对参数小扰动会使害虫和天敌种群出现不同振幅、不同周期的周期震荡现象。若未恰当地选择脉冲周期或天敌投放量,不仅不能消灭害虫还可能使得害虫种群的爆发,同时说明具有非线性脉冲的系统有很强的生物意义。
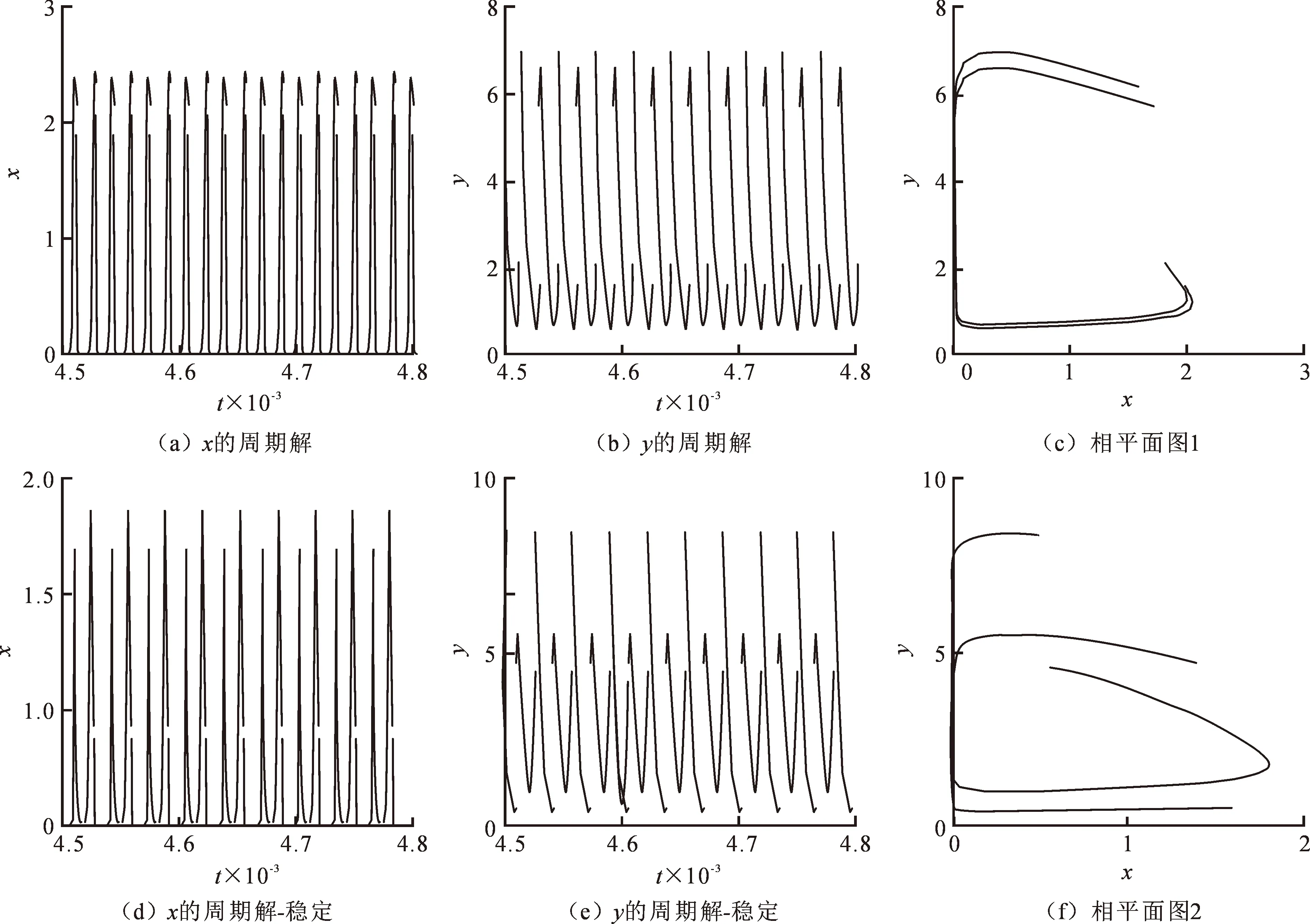
图4 关于图3的2个共存的吸引子Fig.4 Two coexistence stable attractors
5 结 论
农业资源有限是一个普遍存在的现象,严重影响着农作物病虫害的防治,基于资源有限,本文研究了具有B-D功能反应的捕食系统。利用Floquet理论证明了当T
