新型电力系统电流真有效值测量方法与应用

张可可，孙飞跃

（1.上海华东送变电工程有限公司，上海 201800；2.江南大学 物联网工程学院,江苏 无锡 214000）

0 引 言

在电力系统中，电压和电流的有效值、平均值以及峰值是重要的电气参数，是采集和检测中必不可少的内容。受电力系统负荷及电子器件越来越高频化的影响，电力系统中电压和电流波形的高次谐波分量逐渐增大，波形质量很难保证，这为准确检测各种电气参数带来了一定的困难。

1 电流真有效值测量的新型电力系统

有效值的概念是从电流的热效应规定而来的，不论是周期变化的交流信号还是直流信号，只要热效应相等，就可以看作它们的有效值相等。例如，如果某个呈周期变化的交流电流I1通过一个电阻R在一个周期内产生的热量，和另一个直流电流I2通过同样的电阻所产生的热量相等，那么这个周期变化的电流I1在有效值数值上就等于这个直流I2，存在以下关系：

那么直流电流I2的有效值可表示为：

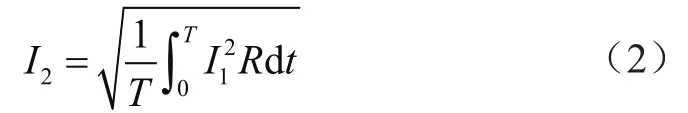
目前市面上的仪表在检测交流电压和电流信号时都是以平均值作为响应，但在实验和实际生产中会有大量的非正弦波，如双极性方波、锯齿波以及畸变的正弦波等，它们都属于交流信号。这时使用计算平均值的方法会存在较大的误差。文献[1]举例说明了被测信号为矩形波、半波整流波、方波以及三角波时，平均值仪表的测量误差分别达到了-44.6%、-29.4%、11.1%以及-3.8%。文献[2]提出了一种基于精密整流电路的交流电压真有效值测量方法，但是在电压信号发生非周期性波动（如噪声）时可能难以实现高精度的检测。文献[3]提出了一种采用智能传感器进行电流真有效值测量的系统设计方案，系统不仅可以精确测量电流真有效值，而且具有良好的与外部总线通信的功能。文献[4]设计了一种基于真有效值转换芯片ltc1968的测量电路，给出该电路对真有效值测量的原理，并证明该电路具有精度高、反应快以及体积小的优点。

1960年，R.E.Kalman提出了离散系统的Kalman滤波，次年与R.S.Bucy合作，将这一滤波方法推广到了连续时间系统中，从而形成Kalman滤波估计理论[5,6]。Kalman滤波是一种时域滤波方法，采用状态空间方法描述系统，算法采用递推形式，数据存储量小，在嵌入式等微型系统中有着广泛的应用前景。

本文面对电力系统中电压和电流有效值的测量，提出的针对电力系统中电流有效值的测量系统在以下两方面的重要意义。一方面实现了电能质量较差时的检测，传统电力系统中的电压电流有效值测量仪大都是以平均值作为响应，通常电力系统中的电压和电流信号都含有一定量的高次谐波和畸变，常规的平均值法无法准确的测量有效值，而本文中的新型电压有效值测量仪通过AD637有效值计算模块，实现了电压电流的真有效值测量[7]。另一方面实现了有效值计算模块输出电平波动时的采样，受波形质量、外部器件参数以及仪器电源供给等因素的影响，有效值换算电路的输出直流电平往往不是平稳的，且含有一定量的噪声，这时直接进行AD采样势必会带来较大的误差，本文通过Kalman滤波器，可以显著降低由直流电平波动造成的量测误差[8]。

2 系统硬件实现方法

2.1 系统的基本组成

本文设计的系统由主控板和电流钳组成，其中主控板由STM32主控芯片及AD637电压有效值计算电路组成，电流钳用以采集电流信号，其二次线圈感应出的电流信号经过采样电阻转化成电压信号输入到电流有效值计算电路中，从而得到与之对应的直流信号，接着由STM32主控板的AD采样端口对电流有效值电路的输出信号进行采样得到该直流电压信号的电压值，经换算后即可得到原始电流信号的有效值。工控屏幕与STM32通过RS485串行接口相连接，用以显示测量数据和操作变更测量选项，USB读写模块与STM32通过USART同步串行接口相连接，用以保存测量数据报告至U盘。

2.2 电压有效值计算电路

当今世界上电路集成的研究十分迅速，这几年出现了各种交变电压电流真有效值AD转换器。如AD637型号的AD转换器在实验中十分常见[9]。AD637的准确度、灵敏性、测量速率、频率特性、电源范围以及功能消耗都满足实验设计要求，用以测量正弦波电流的误差不会超越±1.5%。AD637电压有效值计算电路如图1所示。

图1 有效值计算电路

图1中，CAV是滤波电容，R1是调零电阻，R3是比例因子校准电阻。

通过电流互感器夹取CT柜中电流测试引线的相电流，经过2 kΩ的高精度无感采样电阻产生一个较小的与原始电压同频同相的电压信号，接着由AD637模块进行电压有效值的转换，转换公式为：

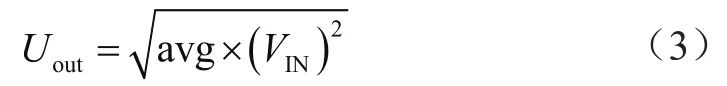
最终得到一个稳定的直流电压，由核心处理器AD采样经过换算后即为实际的交流电压有效值，换算关系为：

式中，Uout为采样电压，Iout为原始电流有效值，R为采样电阻。

3 基于KF的采样滤波算法

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法[10]。由于观测数据中包括系统中的噪声和干扰的影响，所以最优估计也可看作是滤波过程。采用递归的方法解决线性滤波问题，只需要提供当前的测量值和前一个采样周期的估计值就能进行状态估计，需要的存储空间小，且每一步的计算量小。

3.1 计算预测状态方程

由系统状态变量k-1时刻的最优值和系统输入计算出k时刻的系统预测值，计算公式如下：

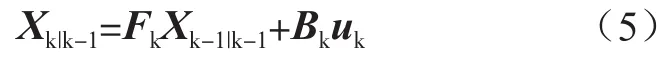
式中，Xk|k-1为k-1时刻状态预测的当前状态；Xk-1|k-1为k-1时刻的最优值；Fk为作用在Xk-1|k-1状态下的变换矩阵，是预测状态变量的依据，本文的状态为一维数据，故Fk设置为1；Bk为控制量的变换矩阵；uk为当前状态的控制增益，本文的应用中设置为零。

3.2 计算预测协方差方程

根据k-1时刻的系统协方差预测k时刻系统协方差，具体如下：

式中，Pk|k-1是k时刻系统协方差矩阵；Pk-1|k-1是k-1时刻系统协方差矩阵；Qk为系统过程噪声的协方差。

3.3 计算卡尔曼增益方程

根据（k时刻）协方差矩阵的预测值计算卡尔曼增益方程。

式中，Kk为卡尔曼增益，是滤波的中间结果；Hk是对象的预测矩阵，本文应用中由第3.2章节所计算出的Pk|k-1是个一维矩阵，故Hk可设置为1；Rk是对象测量噪声的协方差矩阵，作为一个初始数值输入滤波器，该值会影响到滤波器的滤波效果，取值越小收敛越快，故需要结合实际需求寻找合适的数值。

3.4 更新最优值方程

根据状态变量的预测值和系统测量值计算出k时刻状态变量的最优值，计算公式如下：

式中，Xk|k为k时刻状态变量的最优估计值；Zk是对象的测量值。

3.5 更新协方差方程

计算k时刻协方差矩阵的公式如下：

式中，Pk|k为k时刻的协方差矩阵；I为单位矩阵。

4 实验验证

为验证本文提出方法的有效性，使用MATLAB数值仿真软件验证采样滤波算法，给定一个电压为 V的直流信号，并加入了均值为0 V、方差为0.05 V的噪声。卡尔曼滤波过程噪声协方差初始值设置为0.001，观测噪声协方差初始值为0.543，估算协方差初始值设置为0.02。滤波后的结果如图2所示，虽然原始的波形中含有大量的噪声，但经过卡尔曼滤波器后依然可以得到一个较为稳定的波形，为后续的单片机AD采样准确性提供了保障。

图2 电压信号卡尔曼滤波结果

为了更进一步验证本文提出方法的有效性和准确性，制作了一个电流检测仪原型样机，并通过函数发生器分别测试产生不同有效值的正弦波、三角波以及方波电流信号，给定电流有效值分别为0.5 A、1 A、1.5 A、2 A、2.5 A，正弦波测试结果如表1所示，三角波测试结果如表2所示，方波测试结果如表3所示。

表1 正弦波电流检测结果

表2 三角波电流检测结果

表3 方波电流检测结果

由实验结果可以看出，本原型样机可以实现精准的电压电流真有效值检测并具有较高的检测精度。

5 结 论

本文的研究成果主要适用于电力系统中电压和电流有效值的测量，具有较高的精度，也适用于多种波形的有效值测量，并用过实验验证部分证明了其可行性。此外，本文的研究成果可应用于供配电公司等部门以及对检测精度要求较高的场景，其在电网升级改造的背景下与电网安全运行发展目标相一致，具有较好的经济效益、示范效益以及社会效益。