人工粗糙度对矩形弯曲管道流动与传热数值模拟

张 萌,孙 冰

(北京航空航天大学 宇航学院,北京 100191)

0 引言

液体火箭发动机的主要部件之一是推力室,当其工作时,燃烧室内燃气压力可达20 MPa以上,燃气温度可达3 000～4 000 K[1]。如果不采取相应的冷却措施,其室壁材料将无法承受这种恶劣的工作环境。在实际工程中应用最多的冷却方案为再生冷却[2-3]。然而,对于可重复使用、大推力、高室压推力室而言,简单的再生冷却即使结合内冷却有时也不能满足液体火箭发动机的热防护要求。因此,对于可重复使用液体火箭发动机和高室压推力室,局部强化换热技术很自然地成为亟待研究的冷却措施之一[4]。

人工粗糙度作为一种局部强化换热技术,在国内外得到了广泛的研究。所谓人工粗糙度就是在再生冷却通道底面加工出一定分布的凸台,不仅能够增大换热面积,而且可以作为扰流器增大近壁流体湍流度,从而强化对流传热。Hossain等人[5]研究了在冷却通道中设置人工粗糙度对壁面温度和对流传热系数的影响,但忽视了对流场结构的分析。Xu等人[6]讨论了超临界甲烷在内部带有肋结构的加热管内的流动与传热,但只是针对二维模型,不能考虑流动以及传热的三维特性。Kamali等人[7]则主要研究了冷却通道中所添加肋的几何形状和分布等因素对其传热能力的影响。而在实际发动机冷却通道中,由于普遍具有较大的高宽比,因而使得侧壁面传热对整体传热的效果也有很大的影响。

此外,在实际火箭发动机的冷却通道中,由于存在弯曲段,在流动过程中会产生二次流,对流动与传热产生很大的影响。Naraghi等人[8]研究了二次流对冷却通道各个壁面传热的影响。Valentin等人[9]针对不同曲率半径和冷却剂质量流量对二次流的产生及其影响进行了分析。Pizzarelli等人[10-11]比较了采用S-A湍流模型和修正的S-A模型在研究二次流对冷却通道换热的影响方面的优劣,并详细地比较了直型、凹型与凸型冷却通道中二次流的产生以及对各个壁面传热的影响。

针对上述问题,本文对有人工粗糙度的三维弯曲矩形通道进行了仿真计算,对其流场结构以及与二次流的相互耦合作用进行了分析,并讨论了其对冷却通道各内壁面传热的影响。此外,文章还对入口质量流量对结果的影响进行了分析。

1 数值方法

1.1 物理模型及网格划分

本文的研究对象包括内壁和冷却剂两部分,如图1所示。

图1 计算域几何模型与网格划分Fig.1 Geometry and mesh of the computational model

其中,矩形通道高h=5 mm,宽b=4 mm,内壁厚度均为t=1 mm。从入口处到L1=150 mm处为非加热段以形成充分发展的湍流,加热段包括L2=100 mm的长直段、直径Dh=100 mm的90°弯曲段和L3=100 mm的长直段。其中加热段冷却通道底面添加人工粗糙度,凸台为高宽均为0.2 mm的矩形凸台,凸台长度横贯通道底部为4 mm,沿通道间隔p=5 mm。加热段采用非对称加热以模拟实际火箭发动机中的受热状况,受热面为冷却通道外底面。由于几何模型的对称性,只取半个模型作为计算域。网格划分也如图1所示,全部区域采用结构化网格,其中流体域靠近壁面处加密以捕捉边界层内的流动特征,无粗糙度情况下网格总数约为112万,有粗糙度情况下由于在粗糙度附近进行了加密,因此网格总数约为140万。流体近壁面处的y+值为30～60之间,符合标准壁面函数所需的30～300之间的要求。

1.2 控制方程及湍流模型

采用Fluent 15.0进行计算,流体域控制方程为三维Navier-Stokes(N-S)方程

(1)

式中：div为该矢量的散度；ρ为控制体密度；U为速度向量；φ为待求标量值；Dφ为广义扩散系数；gradφ为φ的梯度；Sφ为单位控制体体积的广义源项。当φ，Dφ及Sφ取不同的矢量时,该方程能代表连续方程、动量方程、能量方程和组分方程[12]。固体域热传导控制方程采用傅立叶导热方程,湍流模型则采用RNGk-湍流模型,在文献[13-15]均采用此模型求解流体在弯曲管道内的流动与传热,并指出其能够有效准确地求解受强曲率影响的管道内及近壁区湍流流动。近壁区域处理采用标准壁面函数。

1.3 边界条件及参数

计算所需要的边界条件按照如下的方式给出：入口边界取质量流量入口,质量流量为0.2 kg/s,温度为120 K。出口边界取压力出口,出口压力14 MPa。冷却剂取甲烷,由于其所处压力远高于其临界压力4.9 MPa,因此其处在超临界状态且物性参数变化比较平缓。在此基础上,为了排除物性变化对结果的干扰,假设冷却剂各物性参数保持不变,取其处于200 K时的物性如表1所示。内壁材料取铜,其导热系数为387.6 W/m·K。由于通道几何形状的对称性,只取半个几何模型作为计算域,因此冷却剂侧对称面取对称边界条件,流固耦合壁面取无滑移条件,除加热面和流固耦合壁面以外其余壁面均取绝热边界。加热面取常热流密度,热流密度取定热流密度q=20 MW/m2。

表1 模型所采用冷却剂物性参数Tab.1 Coolant properties used in the model

1.4 网格无关性验证

在进行结果分析之间,首先验证本文计算结果与网格无关,采用无粗糙度工况作为验证算例,取3种网格数如表2所示。图2给出了3种网格数目下加热段L2区域的壁面温度沿流向变化,由图可知,3种网格数目计算所得结果都非常接近,粗网格计算结果与其他两种相比存在一定的区别,而后两种网格数目所计算得结果几乎完全一致。因此综合考虑计算精度与计算成本,选择中间数目的网格来进行后续的研究。

表2 网格无关性分析不同网格设置Tab.2 Various grid settings of grid independence analysis

图2 3种网格数目下L2加热面壁面温度沿轴向变化Fig.2 Streamwise variations of wall temperature of L2for three grid levels

2 计算结果分析

2.1 流场结构分析

图3为有人工粗糙度的冷却通道底面近壁区域流线图,从图3中可以看出,由于人工粗糙度的存在,使得流场结构有了较大的改变。首先使得近壁区域的层流结构遭到破坏,在每个凸台下游处产生了局部的涡旋。其次,冷却剂在流经凸台时会使流线受到压缩,进而产生了局部的高流速区域。

图3 有人工粗糙通道底部近壁区域流线图Fig.3 Streamline diagram of near wall region at the bottom of cooling channel with ribs

图4给出了两种工况下弯曲段对称面速度云图,由图4可知,当流体进入弯曲段时,由于离心力的影响,流体速度中心会逐渐向通道底部移动。此时会在通道横截面上产生二次流,对传热产生很大的影响。而当在通道底面设置人工粗糙度时,会使得靠近底面处的流速受到影响,速度中心向靠近通道顶部的方向移动。

图4 弯曲段对称面速度云图Fig.4 Velocity contour of symmetrical plane in curved section

为了进一步讨论由于曲率所引起的二次流与人工粗糙度的相互耦合作用,在弯曲段分别取θ=0°,45°,90° 三个截面，如图1所示,其中,θ=0°表示x=250 mm截面,即长直段与弯曲段的连接处。图5给出了各截面上的速度云图与速度矢量图,从图5中可以看出,当θ=0°时,无人工粗糙度的冷却通道,在通道中心流速较高,随着向壁面处的靠近流速会逐渐降低。而对于有人工粗糙度的冷却通道而言,由于底面处存在的凸台会破环流动边界层,使得靠近底面处的流动受到了干扰,因而其流速的中心有明显向冷却通道上部移动的趋势,导致整个流场整体看上去就像是被“压扁”,而中心流速也相较于无人工粗糙度的偏高。当θ=45°时,随着二次流的产生,流体会产生向通道底面移动的趋势,因而会导致流速中心也会随之下移。在越靠近中心对称轴处,这种下降的趋势就越明显,进而使得整个速度云图呈现出不规则的形状。此外,由于有人工粗糙度的冷却通道靠近底面处的流动受到干扰,其流速中心向底面移动的程度会较轻。而当θ=90°时,随着二次流的进一步发展,流速中心已完全移动到冷却通道下半部分。而在冷却通道的上半部分,有人工粗糙度的冷却通道内轴向流速相对较高,表明其受到二次流动的影响相对较小。

此外,通过分析二者的速度矢量图可以发现,当θ=0°时,二者的速度矢量图没有明显的区别,因为此时并没有产生二次流。当θ=45°时,随着二次流的产生,二者均产生了所谓的“迪恩涡”[16],但在有人工粗糙度的冷却通道中所产生的迪恩涡的范围相对较小且距离底面较远。而θ=90°截面上的速度矢量图则更加明显地反映了这一趋势,为了定量分析二次流与人工粗糙度产生的涡流强度的变化规律,在这里引入螺旋度的概念,其定义为

H=(V)·V

(2)

式中：H为螺旋度;V为速度矢量。

二次流与涡流的叠加强度可以通过螺旋度的绝对值来测量,图6给出了两种情况下沿流动方向螺旋度变化。由图6可知,在L2长直段,无粗糙度情况下的螺旋度为0,因为此时还没有产生二次流。而对于有粗糙度的情况而言,由于粗糙度的存在使得流体在靠近壁面处产生涡流,因此其在L2处存在一定量的螺旋度。随着流体进入弯曲段,由于逐渐产生二次流使得两种情况下的螺旋度均急剧上升。在这一范围内,由二次流产生的螺旋度占主导地位,因此两种情况下的螺旋度相差不大。随后,随着流体逐渐流向L3长直段,二次流的强度逐渐变弱,因此螺旋度也急剧降低。但有粗糙度情况下由于存在由粗糙度产生的涡流,因此其螺旋度高于无人工粗糙度情况下的。

图5 θ=0°,45°,90°截面轴向速度云图与速矢量图(左：无粗糙度;右：有粗糙度)Fig.5 Axial velocity contour and velocity vector graph at θ=0°,45°,90° cross sections (left: without ribs; right: with ribs)

图6 两种情况下螺旋度沿流动方向变化Fig.6 Helicity variation along the flow direction for two cases

2.2 壁面传热分析

图7给出了θ=0°,45°,90° 3个截面上的温度云图,通过对比二者的温度云图可以看出,有人工粗糙度的内壁温度明显较低,表明采用人工粗糙度能够显著地提高换热。随着二次流的产生,对于同一冷却通道,壁面温度也有所降低。这是由于对于凹曲率通道而言,二次流的存在会使传热得到改善。

为了整体比较二次流与人工粗糙度对壁面温度的影响,图8比较了两种情况下加热面壁面温度沿流动方向变化。由图8可知,在L2与L3两段长直段,壁面温度均近乎线性增长。而在弯曲段,如前文所言,由于二次流的作用使得传热得到改善,壁面温度降低。而在加热面上,有粗糙度情况下的壁面温度均低于无粗糙度情况,二者最高壁面温度分别为463 K与424 K。添加粗糙度使得壁面最高温度降低了8.42%,这表明了添加粗糙度可以显著地改善换热从而降低壁面温度。

图7 θ=0°,45°,90°截面温度云图(左：无粗糙度;右：有粗糙度)Fig.7 Temperature contour at θ =0° ,45°,90° cross sections (left: without ribs; right: with ribs)

图8 两种情况下壁面温度沿流动方向变化Fig.8 Variations of wall temperature along flow direction for two cases

为了深入研究人工粗糙度及二次流对冷却通道对流换热的影响,取两种情况下θ=0°,90°截面上顶面、侧面与底面上的对流传热系数进行比较。图9给出了所取截面的示意图,图10给出了θ=0°,90°截面上顶面、侧面与底面上的对流传热系数变化图。其中,对流传热系数的定义为

(3)

式中:q与Twg,l分别为该点处的热流密度和流体与通道接触点壁面温度;Tb流体在该截面处的平均温度。

图9 θ=0°,90°截面示意图Fig.9 Schematic diagram at θ =0°,90° cross sections

通过对图10的分析可以看出,在θ=0°截面上,通道内部各个面上对流传热系数的分布比较均匀,3个面上对流传热系数最高值比较接近且在两个拐角处出现极小值。在该截面上,通道内部有人工粗糙度的情况下的对流传热系数均高于无粗糙度情况下的。而当θ=90°时,由于二次流的产生使得流速中心向通道底部移动。因此对流传热系数的分布也出现变化,越靠近底部,对流传热系数越大。而由前文所述,添加人工粗糙度使得冷却通道中所产生的迪恩涡的范围相对较小且距离底面较远,因此在底面上有人工粗糙度情况下的对流传热系数略低。而在侧壁面上,有人工粗糙度情况下的对流传热系数则明显较高。在通道内部上壁面,两种情况下对流传热系数都比较小,且有人工粗糙度下的对流传热系数略低。

图10 两种情况下θ=0°,90°截面上对流传热系数变化Fig.10 Variation of convective heat transfer coefficients at θ=0°,90° cross sections for two cases

将q与Twg,l分别改为加热面上的热流密度与壁面温度代入公式(3),可得到通道整体的对流传热系数。图11给出了两种情况下弯曲段整体对流传热系数变化,由图11可知,受二次流的影响,两种情况下的对流传热系数沿弯曲通道均有上升的趋势。此外,添加人工粗糙度使得整体对流传热系数有了明显的提高,弯曲段平均对流传热系数提高了13.11%。

图11 两种情况下弯曲段整体对流传热系数变化Fig.11 Variation of convective heat transfer coefficients at curved section for two cases

2.3 入口质量流量对结果的影响

为了验证结论的通用性,对入口质量流量的影响进行了分析。保持其余各条件不变,分别将质量流量改为0.1 kg/s,0.3 kg/s。其θ=0°,90°截面上通道内部对流传热系数变化分别如图12和图13所示。

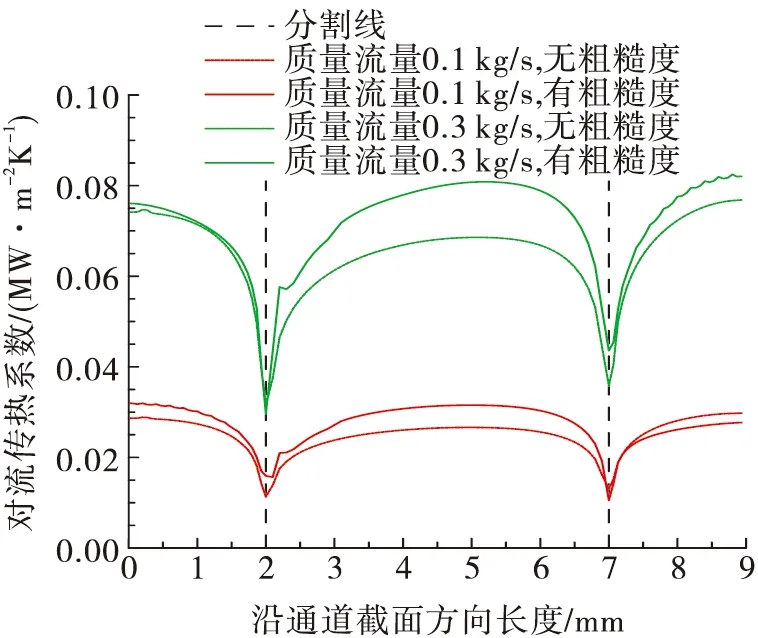
图12 两种质量流量下θ=0°截面上对流传热系数变化Fig.12 Variation of convective heat transfer coefficients at θ=0° cross sections for two mass flow rates

图13 两种质量流量下θ=90°截面上对流传热系数变化Fig.13 Variation of convective heat transfer coefficients at θ=90° cross sections for two mass flow rates

通过对图12和图13的分析可以看出,在不同入口质量流量下,通道内部各个面上对流传热系数的变化趋势基本保持一致。除了θ=90°截面上的通道底面与上壁面以外,其他各个面上的换热都得到了不同程度上的增强。此外,图14给出了两种流量下弯曲段加热面整体对流传热系数变化。通过对图14的分析可知,两种质量流量下弯曲段平均对流传热系数分别提高了11.86%和16.14%。因此可以得出结论,随着质量流量的增加,人工粗糙度对换热的提高作用也越来越明显,表明在冷却剂入口质量流量较大时添加人工粗糙度能够获得更好的收益。

图14 两种流量下弯曲段整体对流传热系数变化Fig.14 Variation of convective heat transfer coefficients at curved section for two mass flow rates

3 结论

为了研究人工粗糙度对矩形弯曲通道内三维流动与传热的影响,本文对有人工粗糙度的三维弯曲矩形通道进行了仿真计算。通过对流场结构以及冷却通道各内壁面的传热进行分析,得到如下结论：

1)在冷却通道底面添加人工粗糙度会使底部流动受到干扰进而导致流速中心上移,中心流速增加。而随着二次流的产生,流速中心会向底部移动。此外,在有人工粗糙度的冷却通道中所产生迪恩涡的范围相对较小且距离底面较远,这个趋势会随着二次流的进一步发展而更加显著。

2)由于二次流的存在使得通道内部各个面上对流传热系数的分布也出现变化,越靠近底部,对流传热系数越大。又因为本文采用的是在底面给定热流密度的非均匀加热,因此,二次流的产生会使弯曲段的换热得到改善,整体对流传热系数上升,壁面温度下降。

3)通过对弯曲段加热面壁面温度与整体对流传热系数的分析可知,通过添加人工粗糙度使得壁面最高温度降低了8.42%,平均对流传热系数增加了13.11%。这表明通过在通道底部添加人工粗糙度能够有效改善换热,降低壁面温度。

4)在不同入口质量流量下,通道内部各个面上对流传热系数的变化趋势基本保持一致。当入口质量流量分别为0.1 kg/s，0.2 kg/s，0.3 kg/s时,弯曲段加热面平均对流传热系数分别增长了11.86%，13.11%，16.14%。这表明随着入口质量流量的增加,人工粗糙度对换热的提高作用也变得越来越明显。

在本研究中,并没有考虑甲烷的实际物性。而在实际发动机中,甲烷在冷却通道中一般处在超临界状态且会经历跨临界过程。在此过程中,由于物理性质的急剧变化会对传热产生很大的影响,因此,后续工作可以考虑结合甲烷实际物性来对人工粗糙度的影响进行分析。