顺层边坡岩体结构的分岔灾变条件
2020-03-05陈笑楠张慧梅
陈笑楠,张慧梅
(西安科技大学力学系,陕西 西安 710054)
0 引言
顺层边坡岩体结构的不稳定性主要表现为边坡离层段的溃屈和坡脚处的剪切滑动[1-2]。应用初始后屈曲理论和突变理论研究边坡岩体的后屈曲性态,其实本质是探讨岩体可能出现的平衡形式的突变和失效形式的演化[2-5]。边坡岩体结构的屈曲属于几何非线性问题,屈曲是失稳范畴的失效,应采用二阶分析方法研究。边坡岩体结构的溃屈属于联系着结构和材料的强度问题,溃屈是破坏范畴的失效,应采用与强度理论相关的准则来判定其失效。初始后屈曲理论突出了研究对象具有平衡形式的突变特征,而岩体结构平衡形式的突变,表达了与边坡岩体相关的分岔特征[3,5]。因此建立在初始后屈曲理论基础上的突变模型,可将具有平衡形式突变的边坡溃屈问题转化为分岔问题来研究。
建立在小变形理论基础上的传统稳定性理论,一般只获得了边坡临界载荷的近似解。如果事先能够给出满足结构位移边界条件的屈曲模态,则可获得其精确解[6-7]。但不能确定结构屈曲后其平衡构形及其模态幅值,也不能确定结构屈曲后其平衡路径和分岔的稳定性。现有的边坡稳定性理论不涉及由于边坡赋存状况决定了的初始缺陷[6,8],因此不能确定其非完善特性的分岔载荷。对于边坡岩体破断机理的研究和所建立的稳定性判据,主要是依据大挠度屈曲实验结果进行直观推测,并结合工程应用加以验证[9-10]。
已有的研究成果表明,关于非完善结构屈曲性态的研究,需要考虑实际结构中存在缺陷这一要素[3,5]。顺层边坡岩体是一个由其赋存状况决定了其初始缺陷的非完善结构,边坡岩体结构的屈曲、后屈曲、溃屈破坏、剪切滑动等与其稳定性相关的问题有待深入研究。本文针对顺层边坡岩体结构的初始缺陷特性和非完善屈曲特征,应用初始后屈曲理论和突变理论等非线性理论,拟将边坡岩体具强度属性的溃屈问题转化为分岔失稳问题来研究,以揭示边坡岩体结构的不稳定性态。
1 边坡岩体的初始屈曲
1.1 边坡岩体的临界载荷
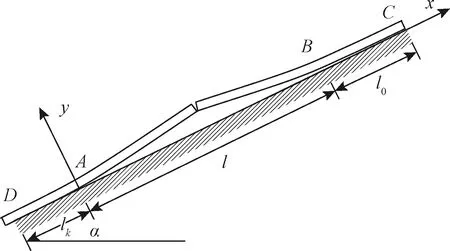
初始后屈曲理论和变分原理指出,只要所研究问题的边界条件确定为相同或相近,可以试取形式上极不相同的位移函数作为模态函数,其结果都是十分接近的。对于图1所示的边坡岩体屈曲力学模型,可取符合其位移边界条件的余弦函数为变形模态。则当边坡岩体处于临界平衡状态时,对于任意的模态幅值am值,由其泛函的二阶变分为零得临界载荷[2,5]

(1)
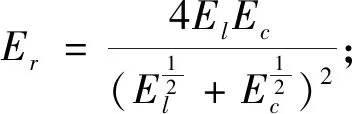
El和Ec——边坡岩体的拉伸弹性模量和压缩弹性模量;
α——岩层倾角与水平地面之间的夹角。

图1 顺层边坡岩体结构的屈曲Fig.1 Buckling for the slope with bedding rock mass
1.2 边坡岩体的模态幅值方程
为了确定边坡岩体在分岔状态下的位移和所承受的载荷,探讨边坡岩体在基本状态附近小邻域的性态,需将泛函的二阶变分在临界载荷因子λ1附近展开为级数,在展开的级数中仅取一阶项,可使边坡岩体结构的非线性稳定性问题线性化[11]。于是,引入基本参数并作近似,原能量泛函数的表达式即转化为如下的简单代数函数[2,5]
F(am,λ)=(λ-λ1)F′2(am)+Π4(w,am)+
Π0(w,am)
(2)
式中,F′2(am)=∂Π2(w,λ)/∂λ。式(2)是一个近似式,是关于模态幅值和载荷因子的一个二参数函数族。由F′2(am)及符合边坡岩体边界条件的屈曲模态,得式(2)各项表达式为
边坡岩体基本平衡状态附近的平衡构形可由代数函数F(am,λ)的驻值来确定,当驻值为本征值的最小时,平衡构形才是稳定的。为了确定边坡岩体的模态幅值和平衡构形,可利用驻值原理∂F(am,λ)/∂am=0,得平衡模态幅值方程

(3)
式中,
式(3)的点的集合是一个临界流型,其几何形态是一个平衡曲面。临界流型具有突跳、双模态、不可达等特性[12]。由式(2)知,当λ=λ1时,使模态幅值am减少为零的变形路径是真正的后屈曲平衡路径。
2 边坡岩体的后屈曲性态
2.1 边坡岩体的分岔方程
位能增量泛函仅在其二次变分中考虑了与载荷因子有关的项,当增量泛函的奇点满足其一阶和二阶导数为零时,可得位能增量泛函奇点的一个子集,即系统状态突变的控制方程

(4)
式(4)也称为尖点突变模型的分岔集方程。当D1>0时,即当作用在边坡岩体上的载荷小于分岔载荷时,边坡岩层保持稳定的基本状态。当D1≤0时,即当作用在边坡岩体上的载荷大于分岔载荷,并D1和D2同时满足分岔集时,体系从基本平衡状态到达邻近的平衡状态。
2.2 边坡岩体的分岔载荷
为了确定边坡岩体屈曲后分岔点附近的邻域及溃屈状态下的推力,将D1、D2代入分岔集方程,得跨越分岔集的载荷增量
(5)
式(5)以载荷增量的形式给出了分岔点附近的邻域,而跨越分岔点的载荷增量是由初始缺陷确定的。应用与增量泛函二阶变分为零相一致的条件,以及几何边界条件,得载荷参数的最小值λ1=1。因此,由式(1)和式(5)可确定边坡的分岔载荷

(6)
式(6)表明,在与临界载荷相邻的载荷下,缺陷结构的屈曲性态与完善结构是很不相同的。
2.3 边坡岩体的模态幅值

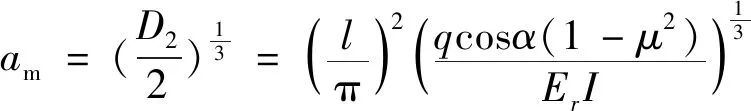
(7)


(8)
即

(9)
时,边坡岩体的屈曲模态构形平衡稳定。平衡构形的稳定性表明,边坡岩体从基本状态到达至邻近的后屈曲状态后还可继续承载,后屈曲平衡路径的性态揭示了后屈曲状态下边坡岩体的平衡稳定性,平衡路径上任一点表达了作用在边坡岩体上的载荷和屈曲后的位移。
2.4 边坡岩体的破断位置
显然,满足边坡赋存状况边界条件的变形模态在闭区间[a,b]上连续,且在开区间(a,b)具有导数。由Lagrange中值定理,在该区间内至少存在一点ζ(a<ζ w1(b)-w1(a)=(b-a)w′1(ζ) (10) (11) (12) 于是,取符合赋存状态的ζ的最小值,即n=1,可得图1所示边坡岩体溃屈破断的位置为 (13) 由式(13)知,边坡岩体的溃屈破断位置与边坡的倾角、边坡离层长度以及模态幅值有关。也就是说,边坡岩体溃屈破断的位置是由边坡结构的结构特征、岩体材料、物理力学参数等确定的。 边坡岩体沿坡面的长度可分为上部滑动段BC、中部离层段AB和下部剪切段AD(图1)。当边坡岩体的离层段处于临界状态时,由边坡位能泛函的二阶变分为零确定的临界载荷与上部滑动段提供的推力,可给出脱离底层的离层方程为 (14) 式中:P0=(qsinα-qcosαtanφ-c)l01——边坡岩体单位宽度下滑力, φ——层间摩擦角; c——黏结力; l——边坡已与下层岩石脱离的长度; l01——可在底层岩石上滑动的下滑段。 只有当上部滑动段和中部离层段的发育满足式(14)时,边坡岩体结构才会离层屈曲。边坡岩体临界点的平衡稳定性态表明,在推力达到临界值之后,边坡岩体依然能够继续承载,这与线性理论得到的结论是完全不同的。 由式(6)知,对于缺陷结构,在描述其从基本状态转变到某个相邻构形时再增加一载荷增量。因此,边坡的上部滑动段还提供了中部离层段溃屈所需的分岔载荷。设边坡溃屈时上部滑动段为l02,根据溃屈平衡,滑动段l02与溃屈段l之间存在以下关系 (qsinα-qcosαtanφ-c)l02 (15) 式(15)即为顺层边坡岩体结构的溃屈方程。溃屈方程表明,只有当上部滑动段和中部溃屈段的发育满足式(15),边坡岩体结构才会出现溃屈。式(15)即为边坡稳定性发生分岔的充分条件,或溃屈破坏的判据。 边坡溃屈后,破断岩体间的相互作用力即为系统跨越分岔集时的载荷增量ΔP(图2)。设lk为边坡岩体溃屈后坡脚处的剪切极限长度,根据剪切平衡条件有 (16) 边坡岩体溃屈后,由溃屈段破断岩块间的相互推力,可确定坡脚处的剪切极限长度。显然,剪切极限长度与上部滑动段和中部溃屈段无关,只取决于边坡岩体从离层状态演化为溃屈状态而所需的载荷增量。式(16)即为剪切滑动的判据。 由式(16),根据边坡的总体长度和上部滑动段、中部溃屈段及坡脚处残存的长度,即可判定坡脚处会否发生剪切滑动破坏。 图2 顺层边坡岩体结构的溃屈Fig.2 Buckling failure for the slope with bedding rock mass 霸王山边坡的实际长度为1 462 m,属于中厚层灰岩并夹有黏土层夹层的板裂岩体层状边坡,边坡倾角α=40°,容重γ=27 kN/m3,抗拉、压弹模El=3.2×103MPa,Ec=50×103MPa,泊松比μ=0.25,层间摩擦角φ=17°,黏结力C=0.04 MPa,岩层厚度h=10 m,该山坡曾发生过溃屈破坏[7,13]。 边坡单位宽度下滑力P0=(qsinα-qcosαtanφ-c)l01,单位宽度分布载荷q=γh,因此P0=(γhsinα-γhcosαtanφ-C)l01=(27×103h×0.643-27×103h×0.766×0.306-40×103)l01,由该式,即当 时,P0>0,黏土层上覆岩层产生滑动。而上覆岩层厚度h=10 m,因此,可沿黏土层夹层滑动。 根据离层方程式 b1=(qsinα-qcosαtanφ-c)l01, 则离层方程可表示为 a1l3+b1l2-c1=0 当边坡的滑动段l01=150 m时,a1=8.68×104N/m2,b1=10.5×106N/m,c1=28.58×1012N·m 则边坡的离层长度 =652.5 m 边坡岩体的非完善特性主要表现为其初始缺陷致离层段的临界状态偏离了溃屈段的分岔状态。以下给出该工程算例的两种特殊情况: (1)滑动段不再发育、发展,离层段只在其下端进一步发育、开裂、离层。 根据溃屈方程式 (qsinα-qcosαtanφ-c)l02 则溃屈方程表示为 a2l3-b2l2-c2=0 当滑动段停止发育,l02=l01=150 m时,a2=8.68×104N/m2,b2=36.62×106N/m,c2=28.58×1012N·m,则边坡的溃屈长度 =863.5 m 即当滑动段保持150 m,离层段达863.5 m,边坡出现溃屈。 (2)离层段下端发育、开裂、离层,上端增加滑动段,但边坡的离层长度l1=l2=652.5 m不变。由式(14)和式(15)得顺层边坡溃屈方程的增量形式 得47.12×106=0.07×106Δl0,Δl0=673.2 m 即当离层段保持652.5 m,滑动段增长673.2 m,达823.2 m时,边坡岩体出现溃屈破坏。 一般情况下,边坡岩体处于离层段的下端不断发育、开裂、离层,离层段的上端不断转化为滑动段的动态过程中。只有当边坡岩体结构的滑动段和离层段满足离层方程(14)时,边坡岩体结构才会出现离层;只有当边坡岩体结构的滑动段和离层段满足溃屈方程(15)时,边坡岩体才会出现溃屈破坏。 根据剪切滑动判据 得 0.103×106lk=47.12×106,lk=457.5 m 即当lk>457.5 m时,溃屈后才不会被剪断。该边坡的实际长度为1 462 m,如果边坡的滑动段l0=150 m,则边坡溃屈后在坡脚处会被剪断。 图3根据边坡岩体出现的两种溃屈情况,确定了A(150,863)、B(823,652)两点,并进一步确定了该边坡岩体的溃屈直线方程。 图3 边坡岩体的溃屈直线Fig.3 Buckling failure line for the slope rock mass (1)顺层边坡岩体结构是一个由其赋存状况决定了其缺陷的非完善结构。结构的非完善特性在分岔状态下表现为系统跨越分岔集时的载荷增量,边坡岩体结构的溃屈和剪切滑动判据都是依据载荷增量建立的。 (2)边坡岩体临界点的平衡稳定性表明,在推力达到临界值之后,边坡岩体依然能够继续承载。岩体结构处在不断发育的动态过程中,离层临界点属于稳定的平衡分岔,只有岩体结构相关区段的发育同时满足溃屈方程时,边坡才会出现破坏。 (3)边坡岩体结构的离层并不意味其承载能力的丧失。具有非完善特性的边坡岩体结构,表现出边坡的实际溃屈长度偏离其离层长度。算例表明,边坡从离层至溃屈是相关区段不断由离层到滑动演变的一个过程。 (4)初始后屈曲理论是近似的大变形理论,应用初始后屈曲理论可给出结构屈曲后的平衡构形,也可判定结构屈曲后平衡状态的稳定性;突变理论凸显了边坡岩体结构具有的非完善特性,并可将溃屈问题转化为屈曲失效问题来研究。



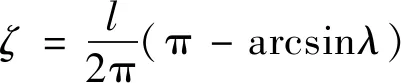
3 边坡岩体的不稳定性态
3.1 边坡岩体的离层方程

3.2 边坡岩体的溃曲方程
3.3 边坡岩体的剪切滑动
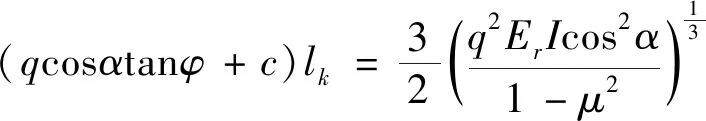
4 工程算例
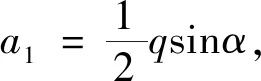
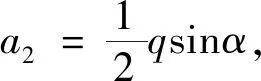

5 结论
