巨型水电站跨省调峰多目标优化方法

苗树敏，王 亮，杜成锐，王金龙，魏 巍，王永灿，何 勇

(1.国网四川省电力公司电力科学研究院，四川 成都 610041；2.国网四川省电力公司，四川 成都 610041；3.华电电力科学研究院有限公司，浙江 杭州 310030)

0 引 言

我国水能资源主要分布在西部特别是西南地区，经过二十年的流域梯级滚动开发，已经形成金沙江、澜沧江、雅砻江、红水河、乌江、大渡河等千万千瓦级干流梯级水电系统，其普遍具有数百万千瓦级巨型水电站和单机容量70万kW及以上水电机组[1]，这些水电工程的发电运行与以就地消纳为主的中小流域梯级不同，需要通过超/特高压交直流输电网架送电至华东、华中、华南等经济负荷中心，满足这些地区的用电和负荷调节需求[2-3]。随着特高压输送通道的不断完善，水电跨省、跨区输电规模不断扩大并快速接近1亿kW，如何有效且高效地发挥西南巨型水电站优质调节作用以满足受端电网的负荷调节要求变得尤为重要和紧迫，亟需探索适合的优化调度模型和方法以适应西南水电系统新的运行要求[4-5]。

近些年，许多学者已经开始关注水电跨省、跨区送电消纳和调度问题并取得了很好的研究成果[6-7]，部分成果在红水河、澜沧江、三峡等水电工程进行了验证和应用[8-10]，本文在此基础上，重点聚焦西南特大流域干流单一巨型水电站跨省送电短期调峰问题，研究多电网差异负荷响应的多目标优化方法，以进一步发展多电网调峰优化理论方法。

结合西南干流跨省送电工程实际，提出巨型水电站跨省调峰多目标优化方法，构建了短期多电网调峰模型，基于正、负理想点采用目标贴近度策略处理多目标问题，耦合出力和流量两类约束优化策略提出自适应遗传算法进行求解，以便快速得到多电网调峰Pareto解集。在优化算法设计中，为满足总发电量控制，改进了种群中个体编码方式；为提高遗传算法后期局部搜索能力，引入了非均匀变异策略；为提高算法收敛速度，采用了自适应交叉变异概率，并耦合父子代混合策略以保留父代中的精英个体。

以溪洛渡电站送电两个省级电网实际问题进行验证，结果显示本文方法能够有效响应多个电网的差异化负荷调节需求，利用多目标Pareto解集能够明晰不同电网间的调峰影响关系，有利于快速得到合理实用的跨省送电方案。上述优化结果为验证方法的可行性和合理性提供了有效的证明。

1 多目标优化模型

1.1 目标函数

本文运用调峰优化目标以充分发挥巨型水电站对受端电网的优质调节作用，并采用经水电调节后的电网余留负荷的平方和最小作为目标函数[11-12]，以保证余留负荷平稳性，减小余留负荷峰谷差，实现水电调峰作用。考虑一般性，下文给出两个省级电网的调峰目标函数

(1)

(2)

式中，T为调度期内时段数；t为时段序号，t=0，1，2，…，T；c′1，t、c′2，t分别为t时段电网1、电网2的剩余负荷，MW。

多目标优化模型

(3)

即在相同约束条件下，求解巨型水电站的发电出力和水库水位，以及不同电网的送电过程，使得两个受电电网的余留负荷平方和都达到最小。

1.2 约束条件

(1)总发电量控制约束

(4)

式中，Eg为水电站分配给g电网的总发电量，MW·h；ωg为水电站分配给g电网的发电量比例；E为水电站总发电量，MW·h。

(2)出力控制约束

(5)

式中，Ng,t为t时段水电站分配给g电网的出力，MW；Nt为t时段水电站总出力，MW。

(3)水量平衡约束

Vt+1=Vt+(Qin，t-Qout，t)×Δt×108

(6)

Qout，t=qt+dt

(7)

式中，Vt、Vt+1分别为t时段初、末水库库容，亿m3；Qin,t为t时段入库流量，m3/s；Qout,t为t时段出库流量，m3/s；Δt为时段长，s；qt为t时段的发电流量，m3/s；dt为t时段的弃水流量，m3/s。

(4)库水位约束

(8)

(5)出力约束

(9)

(6)发电流量约束

(10)

(7)出库流量约束

(11)

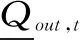
2 模型求解

2.1 多目标处理策略

目标贴近度一般用于在非劣解集中寻找最接近“最优解”，基本思想是先定义一个“最优解”，通过计算各个非劣解与该“最优解”的贴近度，其中贴近度最小者作为“最优权衡解”。

本文采用目标贴进度思想处理多目标优化问题，基本原理为是将各目标值进行标准化，结合权重系数，计算标准化后的目标值到正负理想点的加权距离，通过到正理想点距离相对最小，将多目标优化问题转化为单目标优化问题。

具体步骤如下：

(1)对各目标Fi，分别在其可行域内确定其取值范围[minFi，maxFi]，将{minFi}作为正理想点，{maxFi}作为负理想点，i=1，2。

(2)根据目标贴进度计算公式，计算各目标值的贴近度。

(12)

式中，Fi为任意一个可行解的目标函数值；gi为贴近度，即标准化后的目标值，越小对应的目标越优，正、负理想点对应的贴近度分别为0、1。

(13)

(14)

(4)通过加权距离S1、S2将多目标转化为单目标F

(15)

式中，F值越小，说明该可行解的多目标值越接近正理想点，由此可将多目标转化为单目标。

2.2 模型优化方法

本文采用遗传算法求解多目标优化问题，将不同类型约束条件的搜索策略融入了算法搜索过程中，采用自适应交叉变异概率提高收敛速度，同时采用联赛法选择，并保留父代精英个体，提高遗传算法后期局部寻优能力。

2.2.1主要求解步骤

(1)生成初始种群。根据总发电量控制约束，送往两个电网的电量分别为E1、E2，则水电站调度期内总发电量E=E1+E2。将αk，1t、αk，2t拼接起来可得到k号个体。

(16)

式中，k为个体编号，k=1，2，…，K，K为种群规模；Rand为[0，1]间的随机数。

种群中任意个体按下式计算可得到对应的出力过程。

(17)

式中，Nk,1t、Nk,2t分别为k号个体在t时段分配给两个电网的出力，MW。

(2)自适应交叉策略。交叉概率为

(18)

式中，Pc1=1.0，Pc2=0.6；f为该个体的适应度；fmin、favg分别为种群中最小和平均适应度值。

假设要交叉的个体为k1、k2，交叉位置为cross1、cross2，具体公式为

(19)

(3)自适应非均匀变异策略。变异概率Pm为

(20)

式中，Pm1=0.2，Pm2=0.01；f为该个体适应度；fmin、favg分别为种群中最小和平均适应度。

对交叉种群Genec中每个个体按照Pm判断是否发生变异，对需要进行变异操作的个体按下式计算，生成交叉变异种群Genecm。假设变异个体为k，变异位置为i，则有

(21)

式中，Rand为0或1的随机数；r为当前进化代数；函数Δ(x,y)值域为[0,y]，且函数值接近0的概率随r增大而增大，具体为

Δ(r，y)=y(1-Rand(1-r/R)b)

(22)

式中，R为最大进化代数，Rand为[0，1]间随机数，b为参数，取值范围为[2，5]。

(4)父子代混合。将父代种群Gene0与交叉变异种群Genecm混合，得到一个新的混合种群Gene，种群规模为2Genesize。通过该方法，可以将父代中的精英个体保存到下一代中。

(5)计算目标适应度。将混合种群Gene中每个个体转化为相应出力过程，再按照上文公式计算单目标值F，将其作为适应度；适应度值越小，个体越优。

(6)联赛法选择。对混合种群Gene按照一定的选择概率Pr无重复的选择出Pr×2Genesize个个体，在这些个体中选择适应度最小个体遗传到下一代；重复Genesize次，得到新父代种群Gene0。

(7)对新得到的父代种群重复步骤(2)-(6)，直到达到最大进化代数，输出优化结果。

2.2.2约束处理策略

上文在生成初始种群时已考虑总发电量控制和出力控制约束，故对任意种群中全部个体都能保证满足这两项约束。对于流量和出力两类约束，需要对产生约束破坏的个体进行适应性调整，使其满足全部约束条件，具体策略如下：

2.2.2.1 出力类约束处理策略

这类约束包括机组限制运行区约束和出力限制线约束，即各时段出力需要同时满足上下限范围并避开机组限制区，对此可取交集转化为同一个约束。

(23)

逐时段进行第一轮调整，直至t=T-1。此时若(NT-N′T-1+NT-1)满足上述约束，则调整结束；若不满足，则取最接近边界值并记为N′T，将取为(N1-N′T+NT)，进行第二轮调整，此时只要某一个时刻出力能够直接满足上述约束即可结束调整。

2.2.2.2 流量类约束处理策略

这类约束包括出库流量约束和发电流量约束，首先采用以电定水算法，将经出力类约束调整后的出力过程转化为流量过程，具体步骤如下：

(2)按以下过程计算时段末水位Zt+1对应的出力Nt。

(24)

若qt不满足约束，则进行如下调整

(25)

若满足约束条件，则跳过上述调整，以水定电计算Nt。

(26)

式中，Z(·)为水位库容关系函数；Zw(·)为尾水位-泄量关系函数；NHQ(·)为水-电转换关系函数。

(4)根据Nt所处出力区间，确定时段末水位上下限，然后重复第2、3步，直至满足精度要求，对应的水位和流量即为所求值。

3 实例分析

本文通过溪洛渡水电站跨省送电实际工程进行模型方法验证。溪洛渡左右岸各有9台机组，单机容量70万kW，总装机1 260万kW，其中左岸机组接入国家电网，主要向华东、华中地区及四川省送电；右岸机组接入南方电网，主要向广东和云南省送电，本文主要考虑华东和南方两个受端省级电网，分别记为电网A和电网B。溪洛渡正常蓄水位600.00 m，汛限水位560.00 m，死水位540.00 m，具有季调节能力。由于受端电网间的日负荷差异较大，如何安排溪洛渡水电站跨省送电以有效缓解电网调峰压力是非常重要和必要的。下文主要从单目标调峰和多目标调峰两个方面分别进行分析。

(1)只考虑电网A调峰情况，即F1的权重系数取为1，F2取为0时，结果见图1。电网A剩余负荷的平方和为3.217×1011MW2，最大峰谷差21 902 MW，相比等出力情况下剩余负荷平方和3.256×1011MW2减少了1.2%，原最大峰谷差28 389 MW减少了22.9%，具有显著调峰效果；而电网B剩余负荷的平方和为1.746×1011MW2，最大峰谷差16 172 MW，相比等出力情况下剩余负荷平方和1.737×1011MW2增加了0.05%，原最大峰谷差13 679 MW增加了18.2%，显然未满足调峰需要。

图1 单目标电网调峰情况

图2 单目标电网调峰情况

(2)只考虑电网B调峰情况，即F1的权重系数取为0，F2取为1时，结果见图2。电网B剩余负荷的平方和1.724×1011MW2，相比减少了0.7%，最大峰谷差7 734 MW，相比减少了43.5%，具有显著调峰效果；而电网A剩余负荷的平方和3.261×1011MW2，相比增加了0.2%，最大峰谷差31 015 MW，相比增加了9%，显然未有效响应电网的调峰需要。

由上述结果分析可知，在仅考虑单一目标情况下，调峰系数为0的受电电网调峰效果较差，所以有必要进行多电网调峰目标协调分析。

图3 多目标问题的Pareto解集

通过采用不同的目标权重系数，可得到多目标问题的Pareto解集，结果见图3，其中F1、F2的单位均为109MW2。

当λ1∈[0.9，1.0]时，目标F1即电网A调峰目标，其目标函数值始终维持在较低水平，而目标F2即电网B调峰目标，其目标函数值随λ1减小而迅速减小；当λ1∈[0，0.1]时，目标F2为主要目标，其目标函数值维持在较低水平，而目标F1函数值随λ1减小迅速增大；当λ1∈[0.1，0.9]时，F1、F2变化幅度接近，并且数值相对均衡。所以可以认为，λ1∈[0.9，1.0]时，F1占据主导地位，电网A的调峰效果显著；λ1∈[0，0.1]时，F2占据主导地位，电网B的调峰效果显著；λ1∈[0.1，0.9]时，处于均衡区，对两个电网都有一定调峰效果。因此在实际运用中，根据两个电网具体的调峰要求，确定大致的影响程度，即可在相应范围内选择出合适的调度方案。

4 结 论

随着“西电东送”水电输送规模越来越大，西南水电对华东、华南、华中等受端地区的影响也在不断扩大，如何充分利用西南巨型水电站优质调节作用缓解受端电网严峻的调峰压力具有非常重要的意义。本文提出一种巨型水电站跨省调峰多目标优化方法，并依托溪洛渡输电工程进行了模型方法验证，得到了以下结论：

(1)通过单目标和多目标调峰方法分析可知，多目标调峰方法能够均衡地响应不同电网的差异负荷需求，有效利用西南送出水电缓解电网的调峰压力。

(2)采用耦合目标贴近度方法处理多目标优化问题，可以反映多个目标综合优化情况，避免不同目标量级对优化模型的结果影响。

(3)结合实际工程问题特点构建适合的约束处理策略，并融入遗传算法优化框架，可以提升算法的搜索性能，使优化结果能够满足水电调度复杂约束条件，保证优化解的可行性。

(4)随着西南干流巨型水电站集中投入运行，跨省、跨区送电调度运行逐渐成为常态，本文方法可以为实际工程的生产运行提供一种有效的技术手段。