双丁坝间流场及局部冲刷的数值模拟研究
2020-03-05杨旭亮曾庆达肖厅厅
杨旭亮,戚 蓝,曾庆达,肖厅厅
(1.青海民族大学土木与交通工程学院, 青海 西宁 810007;2. 天津大学水利工程仿真与安全国家重点实验室,天津 300072)
丁坝在河道整治工程中发挥着护岸、冲淤和改善航道条件等重要作用。由于丁坝束窄河道,坝头附近流场呈三维紊动特性使局部河床受到强烈冲刷,因此丁坝局部冲刷、安全设计和水毁防护等的研究尤为重要。宁健等[1]通过试验与三维数值模拟方法研究丁坝绕流、局部冲刷及床面变形,对比分析了丁坝坝头发生冲刷的原因,水流作用下泥沙运动的冲坑范围、冲坑坡度情况。张立等[2]通过丁坝冲刷试验观测不同演变阶段局部冲深及展宽过程,在不同来流强度条件下存在非对称特征,局部冲刷坑几何形态呈三维特征,并与来流强度、泥沙粒径有关。孙志林等[3]基于三维数值模拟研究流线型的正态曲面丁坝的水动力特性,并与梯形丁坝相比不仅优化了丁坝周围水流结构,减弱了集中绕流与剧烈紊动,还大幅降低冲刷作用有利于稳定。喻涛等[4]通过水槽概化模型试验研究非恒定流作用下丁坝局部冲刷,分析年最大洪峰流量和洪水总量等情况下丁坝局部冲刷的范围和发展程度。陆晶等[5]通过粗、细两组非均匀沙及不同挑角的交叉水槽试验,观测淹没丁坝附近床面的冲刷坑长度、宽度、最大深度等特征参数,研究冲淤变形对挑角的响应,分析挑角对坝头附近冲刷坑形态与深度的影响。张岩等[6]通过三维数值模拟不同长度单丁坝弯道内的流场结构、流速分布及湍流特征参数水力特性。钟亮等[7]通过水槽试验研究非淹没复式断面丁坝流速分布情况,确定流速高速区分布位置。韩晗等[8]根据实测资料和模型试验,研究连续丁坝回流区引起的河道流速分布和泥沙输移过程。魏文礼等[9]采用数值模拟方法研究丁坝群对弯道流场结构、流速、水面横比降等的影响,验证了丁坝群在改善水流流态,防止岸坡冲於方面的效果。杨兰等[10]采用数值模拟方法研究丁坝群对湍流流场、冲刷形态与机理的影响。
因单丁坝对河道整治效果较弱,往往采用丁坝群系统相互配合,既满足河道整治的需求,又可避免产生新的水害,但各丁坝产生的流场和泥沙冲淤又将对其临近丁坝产生影响,致使丁坝群范围内的水沙运动特征变得复杂多变。许多学者根据试验和数值模拟分析单丁坝挑角、长度和坝型对流场和冲刷的影响,对丁坝群与双丁坝的研究较少,因河道上设置丁坝可以有效束窄河流,使过水断面缩小,坝区流速局部增大,并在回流与主流边界层呈三维特性,使丁坝附近的局部冲刷与泥沙淤积的研究变得复杂,本文选取实际河道整治工程中的双丁坝,根据单丁坝水沙运动特性理论,研究双丁坝间流场及局部冲刷的情况。
1 数学模型
1.1 水流控制方程
在河道丁坝绕流场中,可以用连续性方程和动量守恒方程描述,即
(1)
(2)

本文采用RNGk-ε紊流模型,改进后的方程[11]为
(3)
(4)
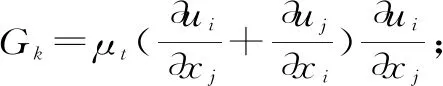
1.2 泥沙输运模型
根据河段情况在研究丁坝局部冲淤中河床推移质泥沙运动占主导,不考虑悬移质的影响,采用基于希尔兹数的泥沙输运模型,依据单位宽度推移质的输沙率公式[12]:
(5)
式中,qb为单宽推移质的输沙率;ρs为泥沙的密度;d为泥沙的平均粒径;ub为推移质的平均输运速度;p为泥沙的起动概率。
1.3 丁坝局部冲深
丁坝局部冲刷根据模型试验已建立诸多经验公式,马卡维也夫公式适用于细沙河流的丁坝坝头冲刷,阿尔图宁公式,方达宪等也提出半理论半经验的丁坝坝头冲刷公式。
2 双丁坝水沙模型建立
2.1 三维数值模型及参数
滦河马良子段的丁坝群位于弯曲河道,建设跨度时间较长,属滦河上的危险工段之一,选取该河段与连续布置的2个丁坝作为研究对象,建立三维数值模型,河道模型平面轮廓与实际天然河道一致,分析天然河道上下游非淹没双丁坝之间水沙运动特性。滦河属于宽浅型河道,该区段宽度在100 m以上,水深在2~5 m范围内,深度远小于宽度,因此将河床底部微小的变化地形近似认为平坦,河道横截面简化为矩形。模型长1 400 m、宽1 000 m、高30 m,河床主槽糙率根据实测断面河床质的组成情况取0.025,动床所铺泥沙厚度为20 m,初始双丁坝长度为34.5 m,挑角均为85°,间距为50 m。实测泥沙平均粒径0.13 mm,密度2 650 kg/m3。
为了兼顾运算效率及精度,计算区域分为5个网格块,采用非均匀矩形网格进行划分,其中丁坝附近是主要的研究区域,因此对Mesh Block 3采用嵌套网格进行加密,提高模拟计算的准确性,以便更加详尽的分析水流及冲刷特性。模型及网格划分如图1所示。
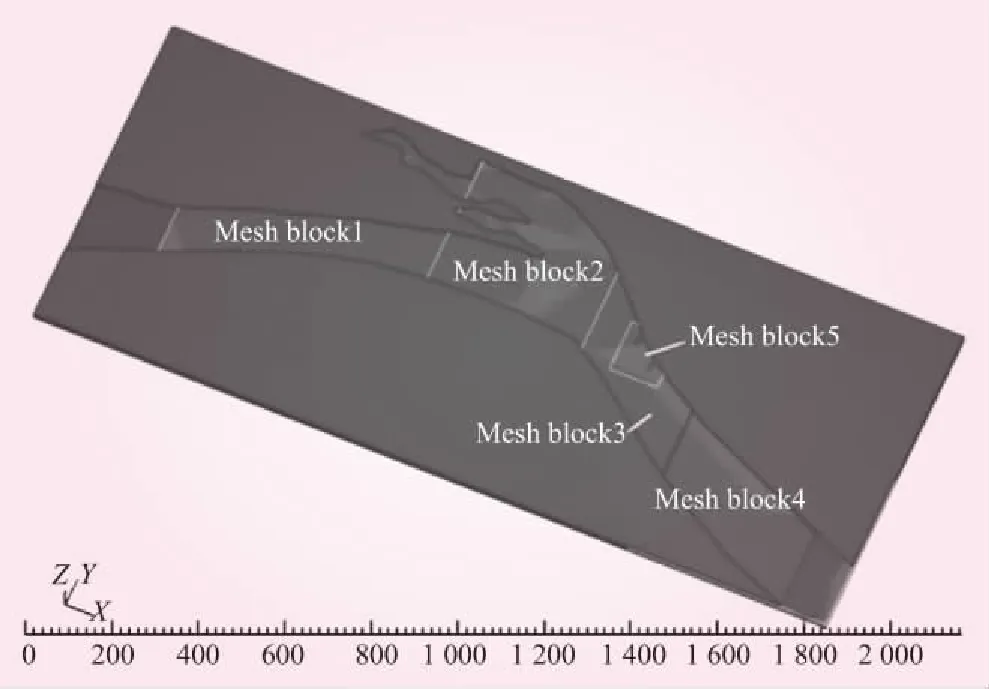
图1 模型及网格划分示意(单位:m)
2.2 边界条件
模型中河道入口Xmin为流量边界,流量为1 160 m3/s, 压力出口Xmax水深为2.5 m。左右岸及河床底部为固壁边界,上表面采用VOF法捕捉液体自由面。初始水流条件控制水深为2.5 m。
2.3 双丁坝数值方案
采用RNGk-ε紊流模型进行数值模拟,根据实际工程设计中的丁坝间距、挑角、断面形状及淹没情况不变,通过控制前后2个丁坝的长度关系,研究双丁坝长度对流场、局部冲刷与泥沙冲淤演变的影响。因丁坝长度直接影响工程量与河势控制效果,为了对比检验计算结果的合理性,分析丁坝的联合效应,探讨合理的双丁坝长度关系,以单因素长度为变量设计双丁坝方案见表1。
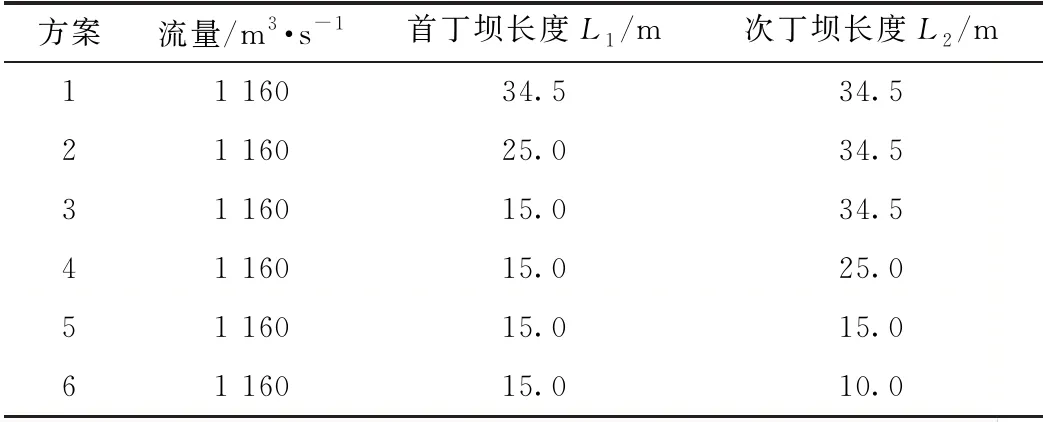
表1 双丁坝设计方案
3 计算结果分析
在河道中修筑丁坝后,影响天然河道原有的水位及平坦床面,由于丁坝对水流的阻碍作用,河流水位随之上升,但这并非最终稳定后的水位;又因过流断面减小,流速增大,河床底部的切应力增大进而下掏床面,泥沙被水流携带至坝后或是下游,河流水位相应回落达到新的平衡状态。通过双丁坝长度关系单因素变化的数值模拟,分别从流场与局部冲深的计算结果进行分析。
3.1 双丁坝对流场的影响分析
调整双丁坝长度关系方案计算所得流场,相同高程的平面流速矢量如图2所示。
方案1~3的次丁坝长度均为L2=34.5 m,对比流速矢量图,随着首丁坝长度缩短,双丁坝周围流场变化明显,方案1中双丁坝坝头位置均出现流速最大值,河道水流平稳,坝后均有明显回流区,丁坝间河道受到掩护;方案2与方案3中流速最大区域均出现在次丁坝坝头,次丁坝后河道流速加快,首丁坝回流区明显能掩护坝间河岸,随着首丁坝长度的变短其挑流作用减弱,而次丁坝回流区有所增大。方案3至方案6的首丁坝长度均为L2=15 m,方案3、4、5中最大流速仍然出现在次丁坝坝头附近,但最大流速明显下降,方案3流速最大值为4.91 m/s;方案6中首丁坝比次丁坝长度大,最大流速区出现在首丁坝附近,河道流速较均匀;随着次丁坝长度的变短,次丁坝挑流作用减弱,且回流区逐渐减小。
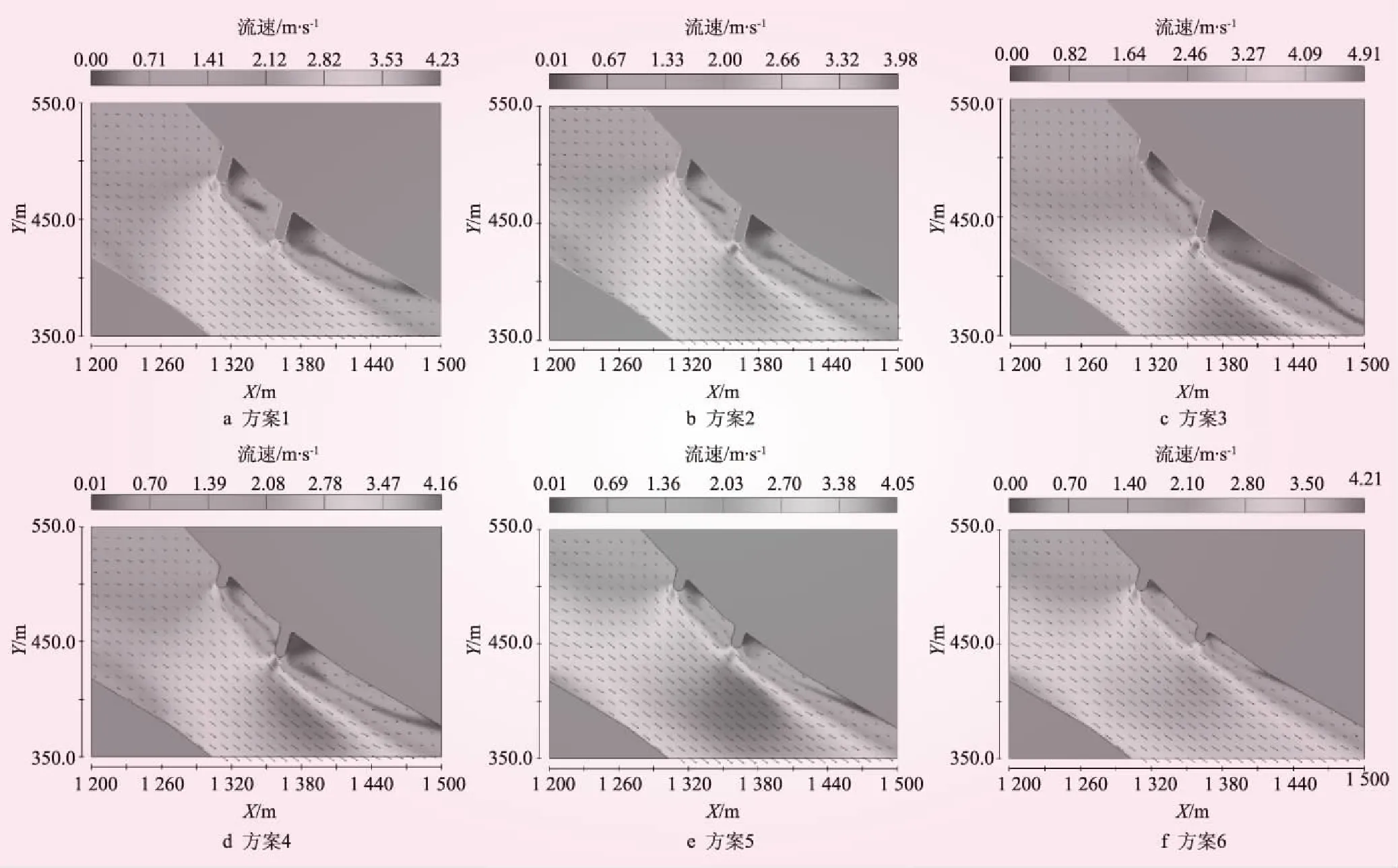
图2 双丁坝不同长度组合的流速矢量
水流经过单丁坝时经挑流作用挑离河岸,随坝后河道断面扩大,水流重新扩散至岸边,呈抛物线形,双丁坝系统先由首丁坝将水流挑离丁坝,水流矢量偏向河道中间一定范围后,还未恢复至河岸又在次丁坝的作用下被二次挑流,水流再次向河道中心聚集,并且随着首丁坝与次丁坝长度变化两次挑流作用也不同,因此双丁坝的合理配置可以提高丁坝挑流效率。
3.2 双丁坝对局部冲深的影响
结合双丁坝方案长度关系特征与数值模拟结果选取3个代表性方案,局部泥沙冲刷情况如图3。
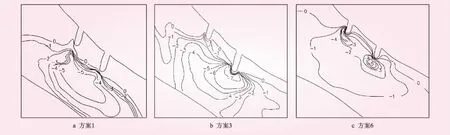
图3 双丁坝不同长度方案的冲深分布(单位:m)
分析双丁坝模型冲刷情况,方案1中双丁坝影响下形成的冲刷坑位置主要在双丁坝之间主河槽,在坝头处连为一体,冲坑底部平坦,冲刷坑坑前等深线密集,坑后较稀疏,坝间近岸处基本不受冲刷。双丁坝长度相差较远时,冲刷坑形态会发生变化,方案1与方案3双丁坝间都形成了一个联合冲刷坑,方案3丁坝长度相差较大,次丁坝坝头处冲刷坑最深,深度为7.05 m,主要由于首丁坝长度较小,冲刷程度较弱,冲刷坑尺寸较小,次丁坝长度较大,冲刷程度较强,冲刷坑较深,且冲刷范围与首丁坝冲刷坑有一定重合,在水流的作用上逐渐融合成一个冲刷坑,如图4所示。方案6中坝头处河床形成了2个相对独立的冲刷坑,尺寸较小,没有形成联合冲刷坑。
河道上布置单丁坝时冲坑出现在坝头附近,由于丁坝的阻水作用及水流绕流作用,坝头处流速较大,水流紊乱,河道切应力增大,泥沙更容易在坝头起动。在长度协调的双丁坝系统作用下,冲坑出现在双丁坝之间,与实际工程中冲刷坑出现的位置相符。
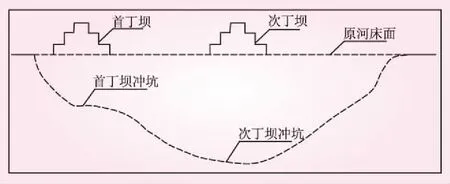
图4 双丁坝长度相差较大时的冲坑示意
4 结 语
通过设计双丁坝的相对长度方案进行数值模拟,在对比验证的基础上进行分析,研究双丁坝不同长度组合对河道流场及河床冲刷的影响,总结了双丁坝协同工作时的主要结论。
(1)河道上设置的双丁坝长度不能太大且相差不大于10 m,长度协调时,坝间河岸被双丁坝回流区掩护,近岸流速较小,河道水流均匀,形成的冲刷坑位置在双丁坝之间河段,坑底平缓,冲刷深度较小,丁坝发挥护岸作用减轻对凹岸的冲刷。
(2)首短次长的丁坝组合中水流经过两次挑流作用后,最大流速区出现在次丁坝坝头,次丁坝回流区尺度增加。首、次丁坝周围形成了联合冲刷坑,最大冲刷深度在次丁坝附近,且冲刷坑上游较缓,下游较陡。
(3)双丁坝方案设计中,盲目地选首长次短或首短次长的双丁坝布置易形成不均匀的河道流场,不利于河道治理与河势控制。因此双丁坝需要严格设计,丁坝长度协调时冲刷坑尺寸较小,河道流场均匀,对丁坝稳定及整治效果较好。合理设置丁坝系统的尺寸,可用较小的工程量有效减小丁坝冲刷坑形态。
