科技园内外科技企业研发效率的比较研究——基于Heckman两步法

吴 建 銮， 赵 春 艳

(西安交通大学 经济与金融学院，陕西 西安 710061)

一、引 言

科技园(Technology Park)，又称高新技术开发区、科学工业园、大学科技园等，是企业技术创新、地区经济发展的重要催化剂，担负着提高我国技术创新水平和推动高新技术产业发展的重任，是国家创新体系的一个重要组成部分，为建设创新型国家做出了积极的贡献。世界上第一家科技园——斯坦福研究园，由美国斯坦福大学弗雷德里克·特曼教授于1951年倡导兴建，开创了世界科技园的先河。我国第一家科技园于1985年由深圳市和中科院共同创建，之后随着大学科技园和高新技术开发区的陆续建立，科技园在我国迅猛发展。据《2018年中国火炬统计年鉴》统计：截至2017年年底，国家高新区数量156个，工商注册企业数185.27万个，年末从业人员1940.74万人，营业收入30.70万亿元；国家大学科技园115个，在孵企业数10 448个，在孵企业总收入340.0亿元。国家高新区和国家大学科技园企业总收入占到了国民收入的37.26%，国家高新区和国家大学科技园在我国现阶段经济发展中发挥着越来越重要的作用。

党的十八大提出实施创新驱动发展战略，明确要求提高科研水平和成果转化能力。作为创新驱动发展的重要支撑和科技服务业的核心载体，从科技企业视角来看，科技园是否提升了科技企业的研发效率，在多大程度上提升了科技企业的研发效率，科技园在我国发达地区和欠发达地区对科技企业研发效率的提升是否存在区域差异，以及科技园对科技企业研发效率的提升是否具有行业差异性？这些问题的研究对于我国科技园产业的科学合理布局、提升科技企业的自主创新能力、培养创新创业人才、推动高新技术产业发展、加速区域经济建设和促进产业结构升级具有重要的理论和现实意义。

本文的创新之处在于：(1)在国内外文献中首次借助面板数据，使用扩展的柯布-道格拉斯生产函数和Heckman两步法对我国新三板的国家科技园园内企业和园外的企业的研发效率进行了测算比较，来验证国家科技园对科技企业研发效率的提升作用；(2)本文首次从区域差异和行业差异视角出发，在控制选择性偏差后测算比较了发达地区和欠发达地区、科技园对不同行业科技企业研发效率提升的差异，来证实科技园对科技企业研发效率的提升作用具有明显的区域差异性和行业差异性。本研究为科技园产业的发展、科技企业研发效率的提升以及新时代我国产业结构升级和解决区域经济发展不均衡问题提供了实证支撑。

二、文献综述

自科技园创建以来，国内外学者对科技园进行了大量研究。归结起来主要分为以下3个方面：

(1)以科技园为研究主体，通过分析科技园的现状、评价体系、运营模式及国际经验来分析科技园的运营机制或为科技园的发展提供意见和建议。如Malecki提出用国家及地方政府对科技园的支持力度、风险资本的流动性等8个指标来构建科技园的评价体系[1]；薛二勇等以欧洲国家科技园发展的典型模式为例研究了创新型国家科技园发展的战略模式[2]；金勇和李莉从大学科技园的战略目标和功能定位入手，提出了建设大学科技园的基本思路[3]；方玉梅和刘凤朝借助熵值法对我国53个国家高新区的创新能力进行了评价，证实了国家高新区创新能力总体较弱，且存在巨大差异[4]；陈劲和张平对我国大学科技园运作机制进行了研究，并阐述了发展大学科技园的必要性[5]。

(2)以科技园为研究主体，大多通过问卷调研取得数据，进而通过构建科技园绩效评价体系或借助一定的计量技术对科技园的经营绩效或效率进行评价。如Sun运用DEA和视窗分析方法对我国台湾新竹科技园六大产业的效率和生产力成长情况进行了研究，发现管理者技能能够提升科技园企业效率[6]；吕萍等通过对园区企业的问卷调查发现，科技园可以通过提供专业服务提升高科技企业的运行绩效[7]；杨震宁等采用探索性因子分析方法从企业需求视角，证实了科技园内企业的总体发展绩效是由多方面因素决定的[8]；刘志春和陈向东运用主成分分析和面板数据模型对我国科技园区研发效率及其时滞效应进行了评价，得出我国科技园产出效率偏低的结论[9]；使用DEA模型测算我国科技园或高新区运行效率的还有余珮和程阳[10]，王敬和汪克夷[11]等。

(3)以科技园内外企业为研究主体，通过比较园内企业和园外企业的差异来评价科技园对科技企业的作用。如Yang等借助面板数据比较了我国台湾新竹科技园内的科技企业与园外的科技企业的研发效率，证实科技园能够显著提升企业的研发效率[12]；Vásquez以西班牙22个科技园为例，使用考虑内生的计量经济模型研究了科技园对科技企业产品创新的作用，证实科技园对科技企业的创新有显著的正向影响[13]；Squicciarini通过比较芬兰科技园内外新兴技术企业及其入驻和迁出科学园区后创新绩效的变化，发现园内企业具有较好的创新绩效[14]。其他相关研究还有：杨震宁等利用科技园企业的问卷调查数据证实，科技园对园内企业创新起到了直接促进作用[15]；刘瑞明和赵仁杰采用1994～2012年间中国283个地级市的面板数据证实，国家高新区的建设显著地促进了地区经济增长，且促进效应存在区域差异[16]；刘雯雯等通过问卷调查从地域性要素出发，探讨并证实科技园的地域要素影响园区内部创新环境[17]。

从上述论述可以看出，国内外学者对科技园做了大量研究且取得了一定成果。然而，现有研究仍存在以下问题：(1)从研究对象来看，学者对科技园企业的研究多集中在几个比较发达的国家或地区如美国、英国和瑞士等，对于发展中国家科技园企业的实证研究相对较少；(2)从研究主体来看，对我国科技园的研究多是从科技园视角出发，运用一定的计量技术对其绩效或效率进行评价，而少有文献从科技园园内外企业出发研究园内外企业研发效率的差异，从而对科技园的作用进行评价；(3)从数据获取方式来看，以往对我国科技园的研究多采用问卷调查为主，研究样本受限，且采用问卷调查方式获取数据容易受主观因素影响，使研究结论可靠性受到质疑；(4)从使用计量方法上来看，尽管有学者以园内外企业为研究对象，对园内外企业的创新能力或研发效率进行比较分析，但是大多研究没有考虑Hackett和Dilts[18]所指出的比较园内外企业时会存在选择偏差，即园内企业并非随机选取，而是满足一定条件的企业才能进入科技园，这就导致园内企业本身的表现就比园外企业表现更好或更差。吴建銮等[19]的研究虽然考虑了选择性偏差但其是以国家级孵化器内外企业为研究对象，且其并未考虑孵化器对企业的孵化作用的区域差异和行业差异效应，同时，其研究使用的是截面数据而非面板数据，从而使样本量受到限制。

基于此，本文通过搜集2012～2016年5年间新三板2363家高科技企业相关数据，使用国际前沿的Heckman两步法控制选择性偏差后，借助扩展的柯布-道格拉斯生产函数分别从整体、区域差异和行业差异视角测算了园内外企业的研发效率及其差异，证实了科技园对科技企业研发效率的提升作用及其区域差异和行业差异效应。

三、研究设计

1.模型设定与研究方法

在本文中，我们定义研发效率为研发弹性，即当研发投入提高一个百分点时产出所增加的百分比。为了测度研发效率，我们参考Yang等[12]的做法同时考虑面板数据模型的个体效应和时间效应，假定企业的生产函数近似为扩展的柯布-道格拉斯生产函数：

(1)

其中，下标i为企业个体，下标t为时间；λt为时间固定效应，表示无形的外生技术进步率；λi为企业固定效应，表示不同企业技术进步差异；Y为产出变量，用企业营业收入(万元)表示；C为固定资本投入变量，用企业固定资产(万元)表示；L为劳动投入变量，用企业员工数(人)表示；M为可变资本投入变量，用企业的营业成本(万元)表示；RD为研发投入变量，用企业的研发费用(万元)表示。

为了估计模型(1)，我们对其两侧取对数将其线性化，线性化后的模型如下所示：

lnYit=λ+λt+λi+αlnCit+βlnLit+γlnMit+φlnRDit+εit

(2)

其中，εit为随机误差项；α、β、γ和φ分别为固定资本投入、劳动投入、可变资本投入和研发投入的产出弹性。

为了比较科技园园内外企业研发效率的差异，传统的做法是分别使用园内企业和园外企业样本对模型(2)进行估计，比较各自的φ值大小或在模型(2)中引入虚拟变量和研发投入lnRD的交乘项，通过比较交乘项前面的系数来判断园内外企业的研发效率的差异。然而，由于企业在进入科技园时有一定的限制条件，其并非随机分配或外生决定的，即存在样本的选择性偏差问题，如果直接使用上述做法对全部企业数据进行分析很可能得到误导性的结论，所以我们采用Heckman两阶段估计模型[20]进行分析以纠正前文所述的样本选择性偏差问题。具体做法如下：

首先，以“企业是否入驻科技园”作为第一阶段估计的被解释变量，以影响企业入园的因素作为解释变量进行Probit估计，基准模型如下式所示：

parkit=β0+β1lnsizeit+β2capintit+β3lnVAit+rdrit+γit

(3)

其中，size为企业员工人数(人)；capint为人均拥有固定资产额(万元)；VA为企业增加值(万元)，用企业营业收入减去企业成本表示；rdr为企业研发强度，用研发费用占营业收入的比重表示。β0为常数项，β1、β2、β3为各变量的系数，γit为误差项。

其次，由于对式(2)直接进行估计可能会存在选择性偏误，所以需要从式(3)的Probit估计中得到逆米尔斯比率(Inverse Mills Ratios)，记为mills，作为第二阶段的修正参数。

最后，将mills作为解释变量引入到模型(3)中以纠正选择性偏误，得到式(4)：

lnYit=λ+λt+λi+αlnCit+βlnLit+γlnMit+φlnRDit+ηmillsit+εit

(4)

其中，η为逆米尔斯比率的系数，若该系数显著，则证明选择性偏误存在，反之则表明选择性偏误不存在。

2.数据及样本

由于新三板挂牌企业均为高科技企业，因此，本文选取新三板2012～2016年5年间所有挂牌企业为研究对象，同时结合我国实际情况，将国家高新区和国家大学科技园统称为科技园，以企业注册地址是否处于科技园内界定园内企业和园外企业。国家高新区和国家大学科技园名单和地址来源于国家科技部火炬高技术产业开发中心和《中国火炬统计年鉴》，新三板挂牌公司名单和研究中所有数据来自万德数据库和大智慧终端。此外，为了考察不同经济发展水平和不同行业科技园对科技企业研发效率的影响，本文定义北京、天津、广东等11个东部省份为发达地区，其他20个中西部省份定义为欠发达地区，行业的划分使用证监会行业划分标准，将全部企业划分为13个行业。经整理剔除缺失数据的样本后，新三板共计2363家企业，其中发达地区1755家，欠发达地区608家。

表1给出了相关变量的描述性统计。从均值来看，科技园内企业的营业收入、固定资产、企业员工数、营业成本、人均固定资产额和企业增加值均远远小于科技园外企业，而科技园内外企业的研发费用相差不大，科技园内企业的研发强度远远大于园外企业的研发强度；从区域角度来看，发达地区企业的研发费用和研发强度远远大于欠发达地区；除研发费用和研发强度外其他变量并没有显示出明显的区域差异和科技园内外差异特征。这说明一方面，科技园对入园企业有一定的要求，从而导致了科技园内企业与园外企业的变量出现了显著差异，而这些要求可能会导致在比较园内外企业的研发效率时出现选择性偏差；另一方面，科技园内企业受专业指导和科技园环境的影响更加重视研发方面的投入，同时，科技园对园内企业研发效率的提升很可能存在区域差异。从标准差来看，除研发费用和研发强度外，科技园内企业其他变量的标准差小于科技园外企业其他变量的标准差。

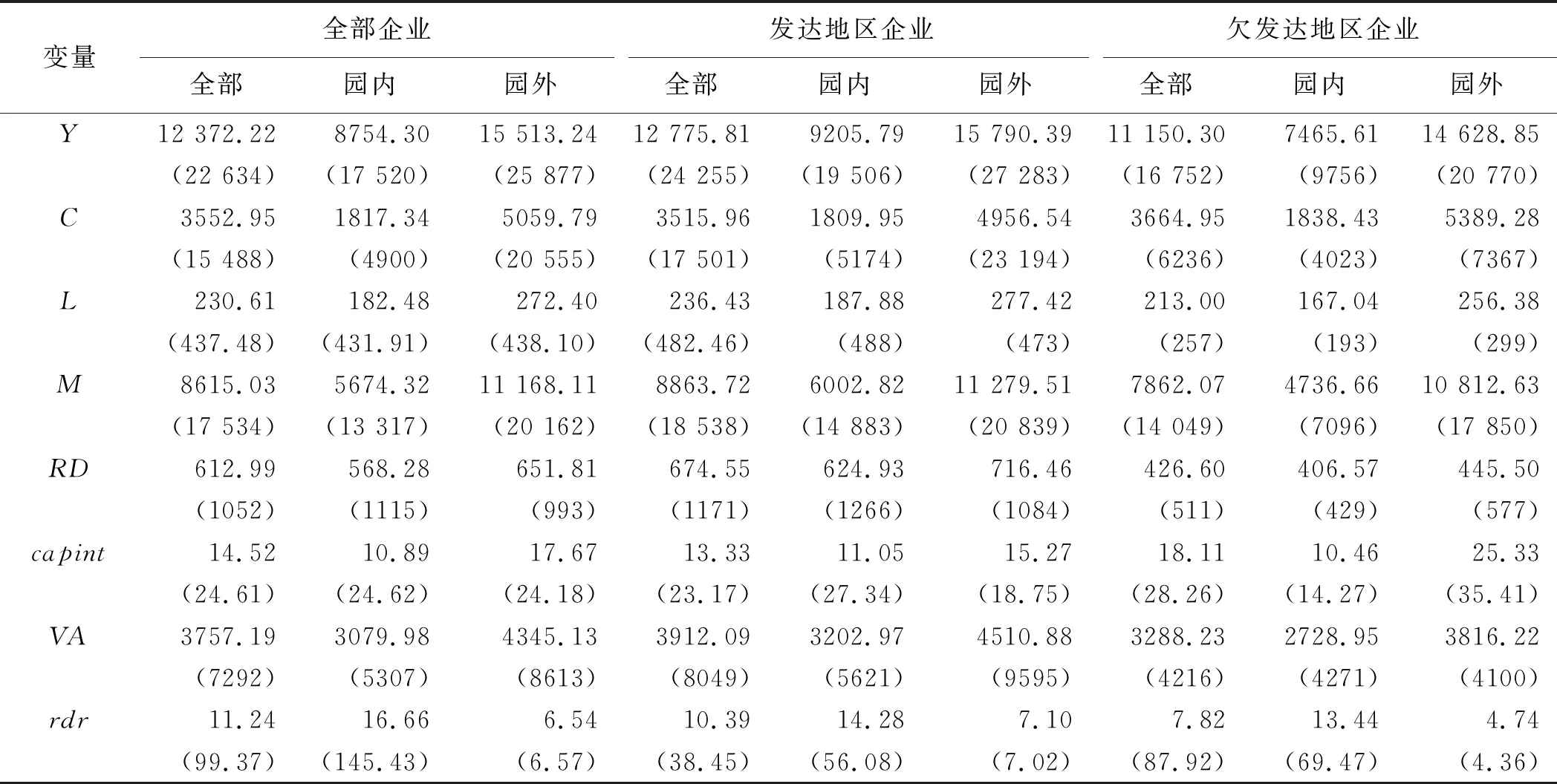
表1 变量的描述性统计

注：表格中的值为各变量的均值，圆括号内的数值为该变量的标准差。

四、实证结果与分析

为了验证和测度园内企业的研发效率是否显著高于园外企业的研发效率、科技园提升科技企业研发效率是否具有区域差异效应和行业差异性，本部分将分别从园内外企业研发效率的整体比较、区域差异视角下和行业差异视角下园内外企业研发效率的比较分析3个方面对科技园影响科技企业研发效率进行细致分析。

1.园内外企业研发效率的整体比较

首先，以新三板2012～2016年所有企业为样本考察科技园对科技企业研发效率的提升作用。为了便于比较，本文将同时给出全部企业、园内企业、园外企业和Heckman两步法的估计结果。Heckman两步法中的Probit模型整体和各变量均通过显著性检验，说明控制方程整体显著且拟合较好。Hausman检验对应的p值均小于5%的显著性水平，说明应该选取固定效应面板模型，4个模型的估计结果如表2所示。

从表2可以看出，整体上来看，4个模型F统计量对应的p值远远小于5%，除模型2的α外所有系数均在5%的显著性水平上显著，说明4个模型均整体显著，拟合效果较好。从4个模型的变量系数来看，可变资本投入的产出弹性最大，其次为劳动投入的产出弹性，再次为研发投入的产出弹性，固定资本投入的产出弹性最小甚至出现了不显著的情况。这不难理解，因为新三板企业大部分是高科技企业，影响企业产出更多的是营业成本、企业人数和研发投入而非企业固定资产。模型1中研发弹性φ为0.0482，说明对于全部企业而言，研发投入每增加1%，产出增加0.0482%。模型2和模型3的研发弹性φ分别为0.0397和0.0656，说明在不考虑选择性偏差的情况下园内企业的研发弹性远远高于园外企业的研发弹性。然而，观察模型4可知，逆米尔斯比率系数η显著为正，说明模型存在选择性偏差，直接比较模型3和模型2的研发弹性可能会得出误导性的结论。模型4的研发弹性φ为0.0526，小于模型3的研发弹性0.0656，说明园内企业的平均研发弹性在入园时就高于园外企业的平均研发弹性。模型4和模型2研发弹性的差异才是由于科技园对企业研发弹性作用的真正提升，模型4和模型2的研发弹性分别为0.0526和0.0397，说明科技园提升了科技企业的研发效率，企业入驻科技园后，企业研发效率平均提升了32.49%。

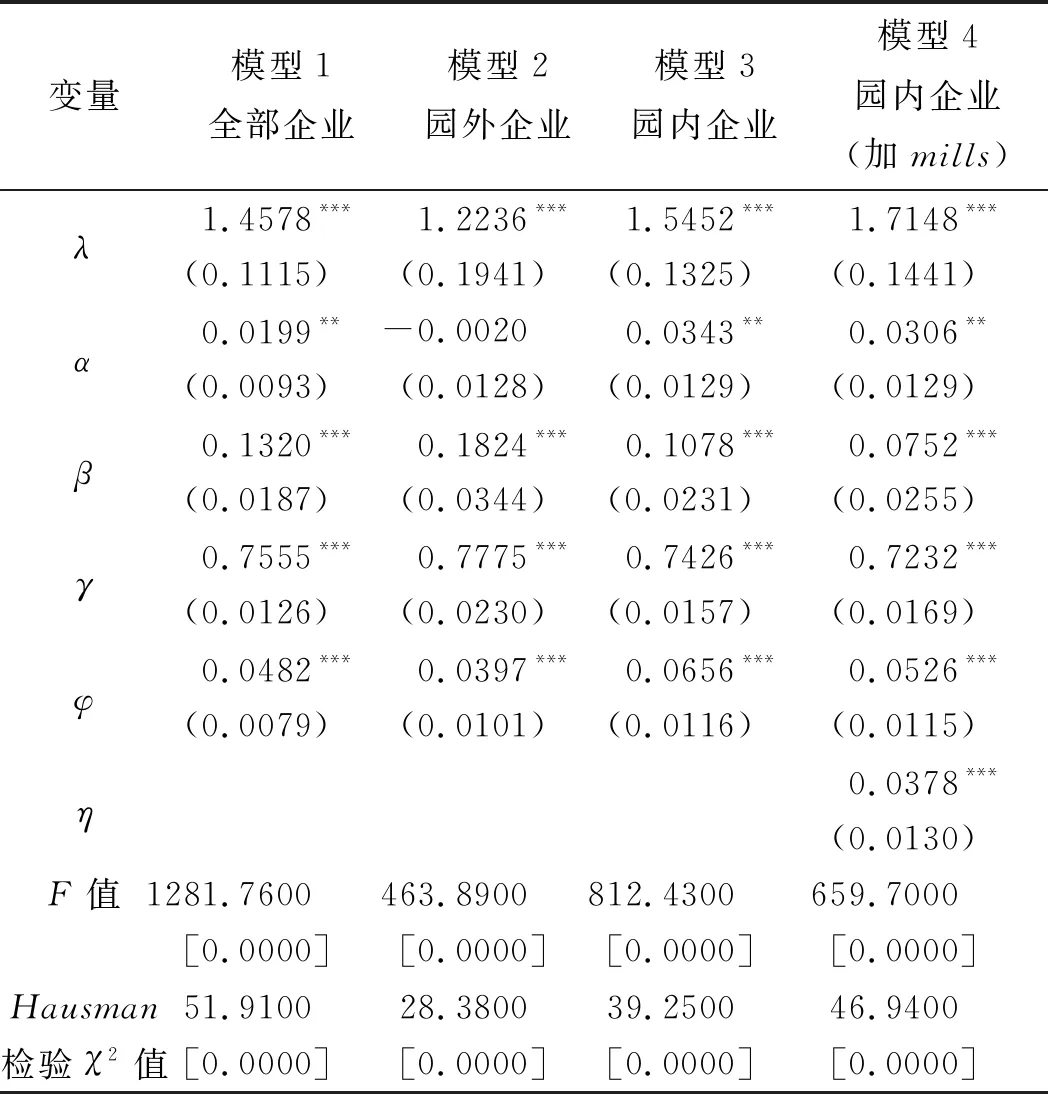
表2 全国新三板园内外企业研发效率

注：系数估计值下方的圆括号内是标准误差；F值、Hausman和检验χ2值下方的方括号内是p值；***、**和*分别表示在1%、5%和10%水平上显著；下同。

2.区域差异视角下园内外企业研发效率的比较

上述分析从整体上证实和测算了科技园对科技企业研发效率的提升，接下来分别通过考察发达地区和欠发达地区科技园对科技企业研发效率的提升程度来说明科技园提升科技企业研发效率的区域差异效应。发达地区和欠发达地区Heckman两步法中的Probit模型整体和各变量均通过了显著性检验，说明控制方程整体显著且拟合较好。发达地区和欠发达地区方程Hausman检验对应的p值均小于5%的显著性水平，说明拒绝模型为随机效应模型的原假设，均应该选取固定效应模型，发达地区和欠发达地区各自4个模型的估计结果如表3和表4所示。

从表3和表4可以看出，除系数α和λ出现了不显著的情况外，其他变量均在5%的显著性水平下通过了显著性检验，且表3和表4中4个模型各变量系数大小顺序均与表2呈现出相同的规律。表3和表4中模型4的逆米尔斯比率系数η显著为正，且两表中模型4的研发弹性均小于模型3的研发弹性，大于模型2的研发弹性，说明两表中模型3均存在选择性偏差，直接通过比较模型3和模型2的研发弹性差异来测算发达地区和欠发达地区科技园对科技企业研发效率的提升会得出误导性的结论。表3模型4和模型2的研发弹性分别为0.0453和0.0417，说明在发达地区科技园提升科技企业的研发效率的幅度不大，企业入驻科技园后，企业研发效率平均提升了8.63%。表4中的模型4和模型2的研发弹性分别为0.0702和0.0437，说明在欠发达地区科技园大大提升了科技企业的研发效率，企业入驻科技园后，企业研发效率平均提升了60.64%。

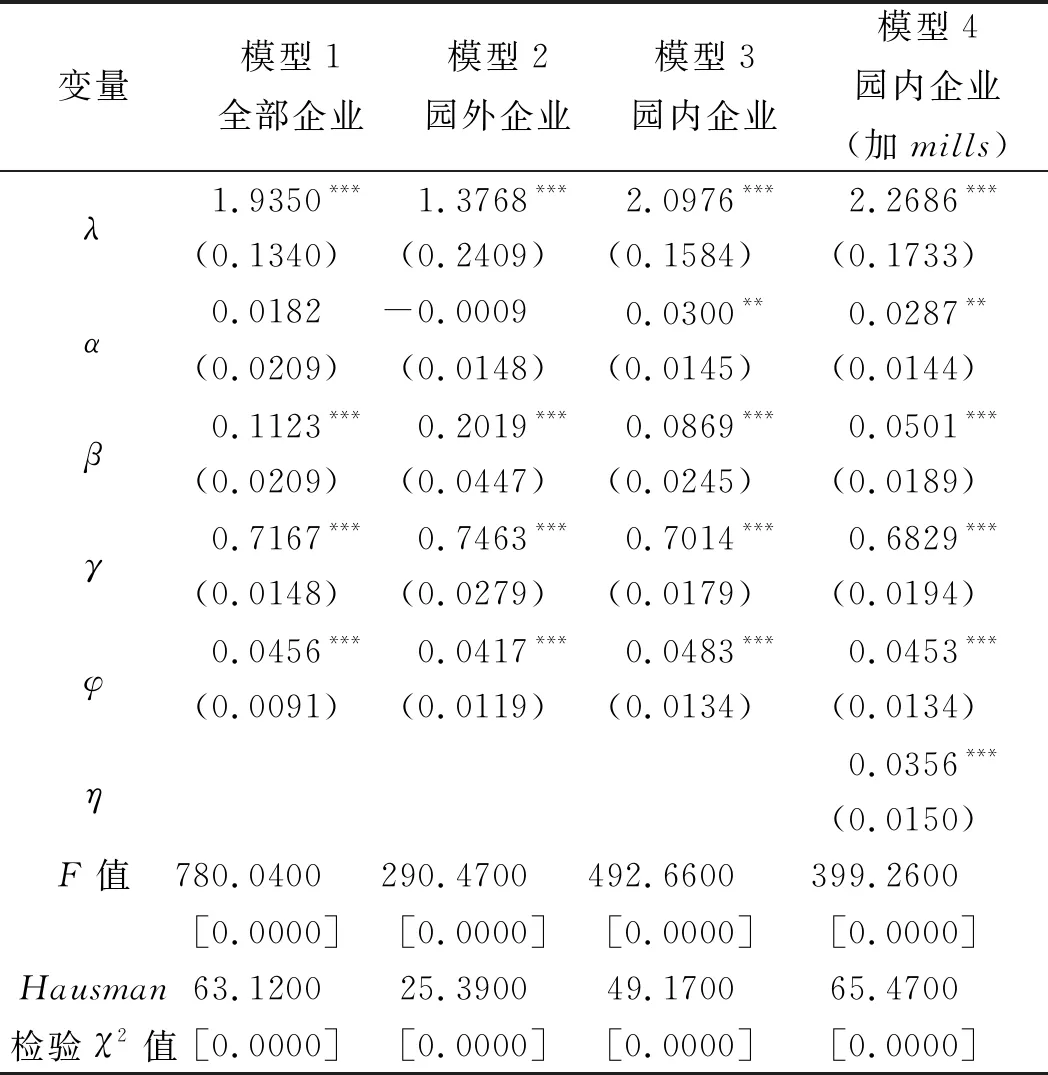
表3 发达地区新三板园内外企业研发效率

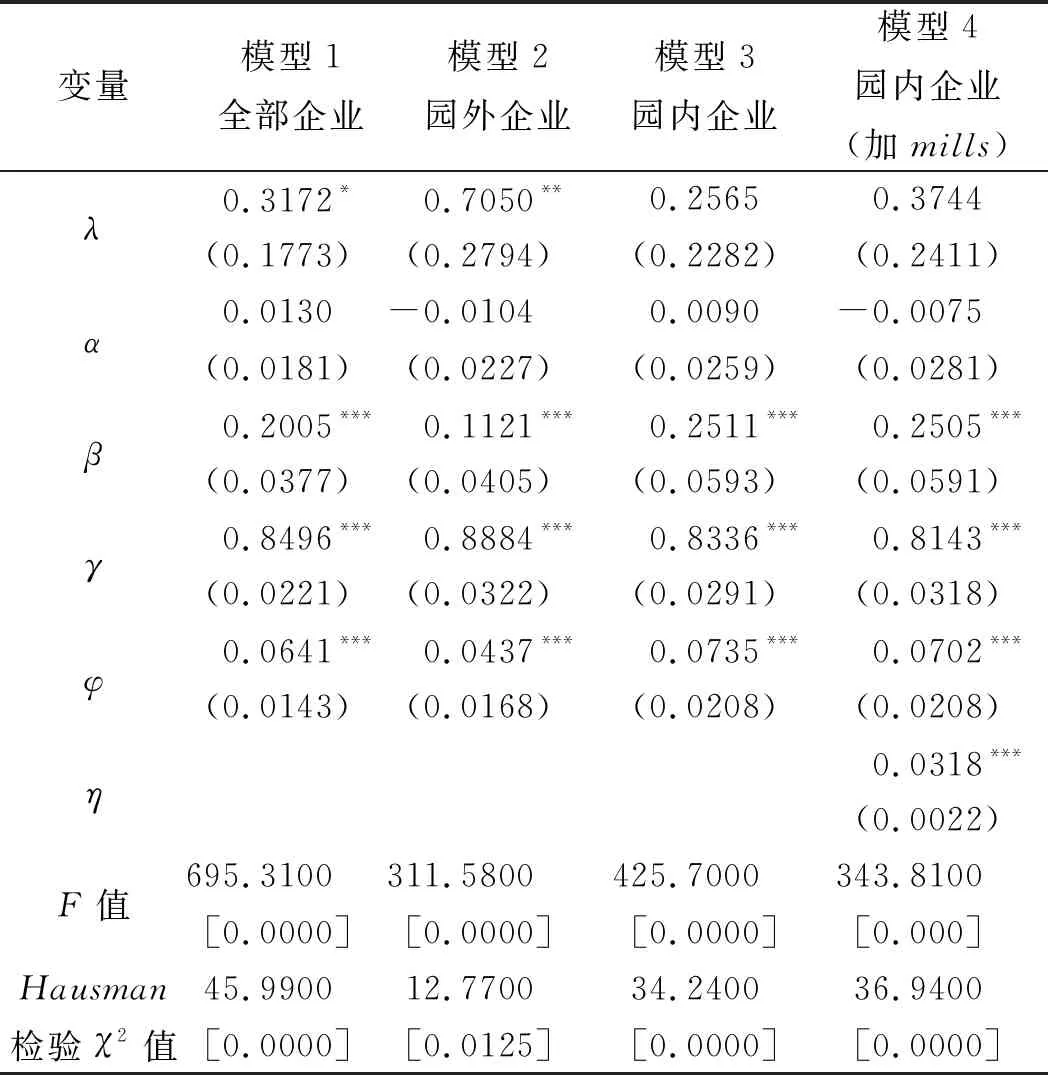
表4 欠发达地区新三板园外企业研发效率

比较表3和表4中各模型的估计结果可知，表3中模型1至模型4的研发弹性分别为0.0456、0.0417、0.0483和0.0453，表4中模型1至模型4的研发弹性分别为0.0641、0.0437、0.0735和0.0702，欠发达地区新三板所有企业、园内企业和园外企业的研发效率均大于发达地区新三板所有企业、园内企业和园外企业的研发效率。从发达地区和欠发达地区科技园对企业研发效率的提升来看，欠发达地区企业入驻科技园后企业研发效率提升了60.64%，发达地区企业入驻科技园后企业研发效率提升了8.63%，欠发达地区科技园对企业研发效率的提升程度远远大于发达地区科技园对企业研发效率的提升程度。欠发达地区的新三板企业研发费用和研发强度远远低于发达地区新三板企业的研发费用和研发强度，而欠发达地区的新三板企业的研发效率及科技园对科技企业研发效率的提升程度远远大于发达地区新三板企业的研发效率和科技园对科技企业研发效率的提升程度，这说明科技企业的研发效率和科技园对科技企业研发效率的提升具有区域差异效应和边际报酬递减规律。在发达地区，科技园发展相对成熟，科技园对科技企业的服务也相对成熟，科技园对科技企业的服务投入的增加带来科技企业的产出增加相对较少，具体表现为发达地区科技园虽然一定程度上提升了科技企业的研发效率，但程度相对较低；而在欠发达地区，科技园及科技园对园内企业提供的服务处于初级阶段，科技园各方面发展相对落后，这种情况下，科技园对企业服务投入的增加会带来科技企业产出的大幅度增加，具体表现为欠发达地区科技园能够在很大程度上提升科技企业的研发效率，因此所表现出来的是科技园对科技企业研发效率的提升具有区域差异效应和边际报酬递减规律。

3.行业差异视角下园内外企业研发效率的比较

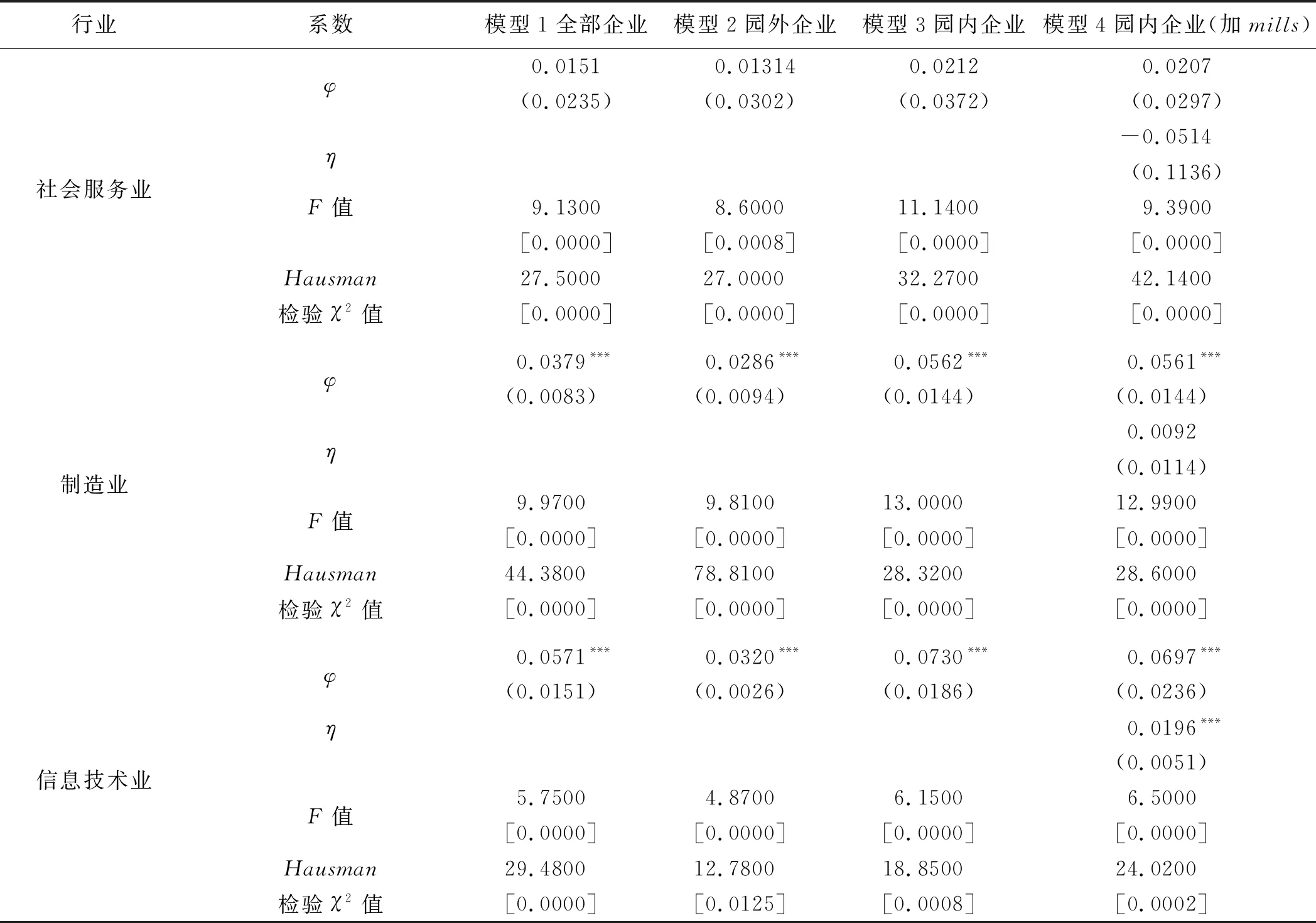
表5 不同行业下新三板园内外企业研发效率

按证监会行业分类标准，将上市公司分为农业、林业、牧业、渔业、采掘业、制造业等13个行业。经统计，在2363家企业中，社会服务业153家、制造业1398家、信息技术业580家，其他10个行业企业数均在60家以下，如果再区分园内园外企业的话，这些行业企业样本数会更小。由于样本数据太小得到的回归结论并不可靠甚至有可能得不到估计结果，因此，本文选取社会服务业、制造业和信息技术业3个行业研究科技园园内外科技企业研发效率的差异性。3个行业4个模型的核心解释变量的估计结果如表5所示。

从表5可以看出，3个行业对应的各模型的F统计量对应的p值均小于5%，说明模型整体显著，拟合情况良好；所有模型Hausman检验对应的p值均小于5%，说明所有模型选取固定效应面板模型是合理的。从各个行业的估计结果来看，社会服务业模型4的系数η不显著，说明不存在选择性偏误；4个模型的系数φ都不显著，说明研发投入对于社会服务业的产出没有显著影响，这是由社会服务业行业性质决定的，社会服务业是劳动密集性行业，其产出对研发投入并不敏感。制造业模型4的系数η也不显著，说明不存在选择性偏误，可以直接通过比较模型3和模型2研发投入变量的系数φ来说明园内外制造业企业研发效率的差异。制造业模型2的研发弹性为0.0286，模型3的研发弹性为0.0562，园内企业研发弹性是园外企业研发弹性的2倍，这说明就制造业行业而言，科技园显著提升了制造业企业的研发效率。信息技术业模型4的系数η显著为正，说明模型3存在选择性偏误，应该使用模型4和模型2比较园内外企业的研发效率差异。信息技术业模型2的研发弹性为0.0320，模型4的研发弹性为0.0697，园内企业研发弹性是园外企业研发弹性的2.2倍，这说明就信息技术行业而言，科技园显著提升了信息技术行业企业的研发效率，且提升幅度大于制造业行业提升幅度。

从上述分析可以看出，科技园在提升科技企业研发效率方面具有明显的行业差异性。对于科技含量较低的社会服务业企业而言，科技园没有提升其研发效率；而对于科技含量较高的制造业和信息技术业而言，科技园显著提升了这些行业企业的研发效率，且对信息技术业企业研发效率的提升幅度大于对制造业企业研发效率的提升幅度。

五、结论和政策建议

基于2012～2016年5年间新三板2363家企业的面板数据，本文利用Heckman两步法从区域差异和行业差异视角研究了国家科技园对科技企业研发效率的影响。实证结果表明：(1)控制选择性偏差后，科技园园内企业的研发效率远远大于园外企业的研发效率，这说明科技园能够显著地提升企业的研发效率。(2)科技园对企业研发效率的促进作用具有区域差异性和边际效用递减规律，欠发达地区科技园对科技企业研发效率的提升远远大于发达地区科技园对科技企业研发效率的提升。(3)科技园对科技企业研发效率的提升具有明显的行业差异性，科技园不能提升科技含量较低的社会服务业企业的研发效率，但能显著提升科技含量较高的制造业和信息技术业企业的研发效率。根据本文所得结论，针对我国科技园产业发展和新时代我国经济增长路径提出如下对策和建议：

(1)鉴于科技园能够显著地提升科技企业研发效率这一结论，我们应当充分利用好这一“经济特区”，不遗余力地深入推进国家科技园和高新区建设，鼓励国家大学科技园和国家高新区的逐步探索和推广，最大限度地提升企业研发效率。

(2)党的十九大指出，中国特色社会主义进入了新时代，我国经济已由高速增长阶段转向高质量发展阶段。而经济实现高质量发展关键在于企业的创新、社会的创新。本文的研究结论说明推进科技园建设能够显著提升科技企业的研发效率，从而让“创新这把钥匙从根本上打开增长之锁”，进而实现经济的高质量发展。

(3)从我国现实来看，一方面我国经济发展不均衡，东部较发达，中西部相对落后；另一方面科技园在我国发达地区和欠发达地区分布极为不均衡。鉴于科技园能够显著提升企业研发效率，且欠发达地区科技园对企业研发效率的提升远远大于发达地区，国家更应该重视国家大学科技园和国家高新区在全国尤其是欠发达地区的推广，从而推动我国欠发达地区经济发展，实现我国中西部地区对东部地区经济发展的追赶，解决我国经济发展的区域不均衡问题。