基于FPGA的椭圆曲线密码二进制域运算实现
2020-03-05沈庆伟宛星斌高莉
沈庆伟,宛星斌,高莉
(安徽建筑大学电子与信息工程学院,合肥230601)
0 引言
椭圆曲线在代数学和几何学上已经广泛研究了150多年之久,有着丰富的理论积累,1985年,Koblitz和Miller将椭圆曲线引入密码学,椭圆曲线密码体制(Elliptic Curve Cryptosystem,ECC)就此诞生[1]。
在目前众多使用广泛的公钥密码体制之中,ECC被认为是每比特提供加密强度最高的一种密码体制。这说明在相同的安全性能条件下,ECC大大缩短了密钥长度。从安全性、计算速度、存储空间来看,ECC拥有着非常好的应用前景
ECC与RSA、ELGamal等公钥密码相比,具有抗攻击性强,CPU占用少,内容使用少,网络消耗低,加密速度快和硬件实现面积更小的特点,是其他公钥密码系统所不能比的。由于ECC的安全性和优势可以广泛应用于电子信息通信、smart cards和无线传感网络终端。这些领域不仅要求具有高级别的安全性,还要具有较快的运算速度和较小的存储空间,ECC满足了这些条件。在当今信息安全邻域中ECC占据重要的位置。随着无线传感器网络技术和物联网技术飞速的发展,在无线传感器网络和物联网内部信息传输加密与解密ECC也发挥着重要的作用。
ECC实现主要分为硬件实现和软件实现。随着通信技术的发展第五代移动通信技术(5G)已成为全球研发的热点[2],这意味着实现密码体制需要更快的运算速度和更高的安全性能,面对这些需求,ECC硬件实现相比软件实现具有的发展前景与优势。那么,实现ECC运算的硬件具有重大意义。由于二进制域上椭圆曲线运算更适合于硬件实现,后面将介绍二进制域上的ECC运算的硬件实现。
FPGA(现场可编程门阵列)往往被人们称为可编程的“万能芯片”,是现在比较流行的硬件设计和开发芯片[3]。理论上,如果拥有规模足够大门电路,FPGA可以通过编程实现任意芯片的逻辑功能,FPGA的核心优点是可编程灵活性高、开发周期短、并行计算可编程效率高。使用FPGA实现ECC二进制域上的运算,不仅提高其运算速度,而且设计开发便捷。
本文介绍了ECC二进制域上的运算的硬件设计,选取了NIST推荐的K-163曲线,实现有限域运算单元实现二进制域下多项式基模加、模乘、模平方、模逆运算。完成RTL代码设计,在Vivado 2017.4软件平台下实现仿真。
1 有限域理论
1.1 有限域的基本概念
域是一类代数结构,它拥有着丰富优良的运算性质,而且应用非常的广泛[4]。例如实数域R、有理数Q、复数域C。这些都属于域,域是代数结构定义了加法(减法)和乘法(除法),满足下列四则运算的基本规律(交换律、结合律、分配律)。
a+b=b+a
a·b=b·a
a+b+c=a+(b+c)
a·b·c=a·(b·c)
a·(b+c)=a·b+a·c
(b+c)·a=b·a+c·a
在组合设计、编码理论、密码学和计算机等许多领域中,有限域具有重要的地位。
有限域又叫伽罗华域,设(F,+,∙)是域,如果F是有限集,则称F为有限域。对于素数p和正整数n,若有限域F的元素个数是pn,那么称有限域的特征为p,可将F记为Fpn或GF(pn)。对于有限域F中任意元素α。
pα=α+α+α+...+α=0
1.2 二进制域的表示方法
二进制域GF(2n)表示方法有三种,多项式表示法[5]、多项式根的表示法和生成元表示法三种。这里介绍后面所用的方法多项式表示法,多项式表示法相对比较容易理解,硬件上实现也比较简单。
多项式表示法:
构造多项式域的数域为F2={0,1},已知多项式集合:
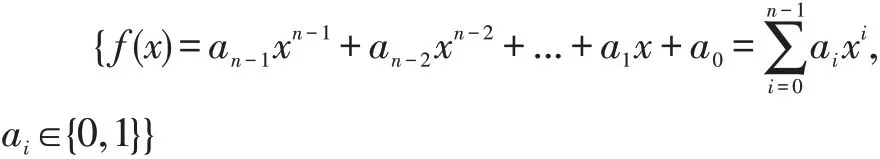
设既约多项式(不可约多项式)为:
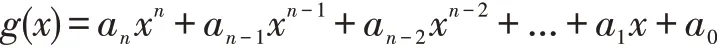
则GF(2n)=GF2[x]g(x)关于模g(x)的同余加法和乘法构成域。
二进制域GF(2n)在编码理论扮演着重要的角色,而在数字计算机和数据传输或是存储系统中同样得到了普遍运用。例如GF(23)=x5+x3+x+1,等价于比特串00101011。
NIST推荐的K-163、K-233、K-409等椭圆曲线,其二进制域分别为GF(2163)、GF(2233)、GF(2409),既约多项式分别为g(x)=x163+x7+x6+x3+1、g(x)=x233+x74+1,g(x)=x409+x87+1。后面的章节针对GF(2163)分析多项式基模加、模乘、模平方、模逆运算。
2 二进制域GF(2n)运算分析
2.1 模加
设有限域为GF(2n),其既约多项式为g(x)=xn+,域中元素有,C(x)=为运算结果。

模加的运算比较容易实现,在硬件设计中模加只需要按位异或即可。
2.2 模乘
设有限域为GF(2n),其既约多项式为g(x)=xn+,域中元素有,C(x)=为运算结果。
模乘运算:
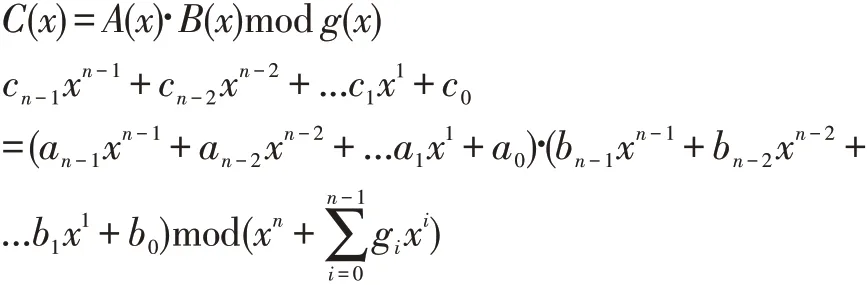
在二进制域乘法除法过程的加法和减法是没有进位的模2计算,按位异或即可。
2.3 模平方
设有限域为 GF(2n),其既约多项式为,域中元素有为运算结果。模平方可以看作模乘的一个特例。
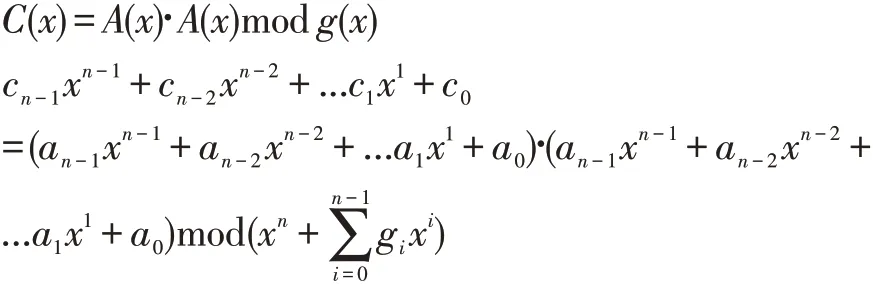
2.4 模逆
设有限域为GF(2n),其既约多项式为g(x)=xn+,域中元素有A(x)=
由费马小定理[6]得:

这样就把模逆运算转变为模乘运算。
3 二进制域GF(2n)算法模块设计
3.1 加法模块
设有限域为 GF(2n),其既约多项式为,域 中 元 素 有为运算结果。
输入:(an-1...a1,a0),(bn-1...b1,b0)
输出:(cn-1...c1,c0)
步骤:

模加模块设计图如图1所示。
3.2 乘法模块
模乘运算分为两个部分,第一部分计算乘法部分,第二部分计算模既约多项式(不可约多项式)部分。由于在计算乘法的过程中是的n位的数被扩展为2n-1位数,所以必须模上n+1位的数使得运算结果在规定的域中。在乘法和求模的过程中,由于是多项式系数的运算,运算过程是没有进位的,加法和减法计算都是按位异或运算。

图1模加模块
使用全并行计算方法实现,全并行计算算方法乘法部分和模既约除法器设计如下所示。
设有限域为 GF(2n),其既约多项式为,域中元素有为运算结果。
乘法算法部分:
输入:A=(an-1...a1,a0),B=(bn-1...b1,b0)
输出:D=(d2n-2...d1,d0)
步骤:
d0=a0∙b0
d1=a1∙b0b1
d2=a2∙
d3=a3∙
...
dn-1=an-1∙
...
d2n-5=an-1∙bn-4d2n-4=an-1∙bn-3
d2n-3=an-1∙bn-2
d2n-2=an-1∙bn-1
end
乘法器内部结构如图2所示。
模既约除法器算法部分:
输入:D=(d2n-2...d1,d0),G=(1,gn-1...g1,g0)
输出:C=(cn-1...c1,c0)
步骤:
将D用D1:D2两段形式拼接
for j从1到D2的位数
if D1>G
则D1=D1^G
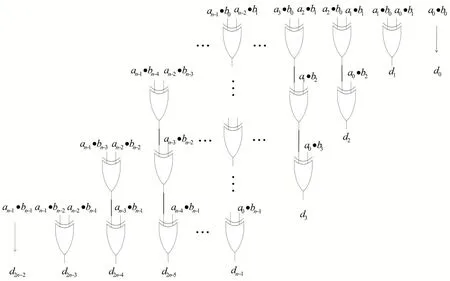
图2乘法器内部结构
D1:D2左移一位
end
C=D1
end
模既约除法器设计图如图3所示。图4为除法器中AXOR模块的内部结构。
3.3 模逆模块
上文介绍将模逆运算用费马小定理转换为模乘运算,A-1=A2n-2,从公式上看计算模逆需要进行大量的乘法运算且运算复杂的相当大,根据文献[5]提供的改进算法如下,以n=163为例。
A22-1←A∙A∙A
A24-1←(A22-1)22∙A22-1
A25-1←(A24-1)2∙A
A210-1←(A25-1)25∙A25-1
A220-1←(A210-1)210∙A210-1
A240-1←(A220-1)220∙A220-1
A280-1←(A240-1)240∙A240-1
A281-1←(A280-1)2∙A
A2162-1←(A281-1)281∙A281-1
A2163-1←(A2162-1)2
这个算法成功的降低模乘运算的复杂度。
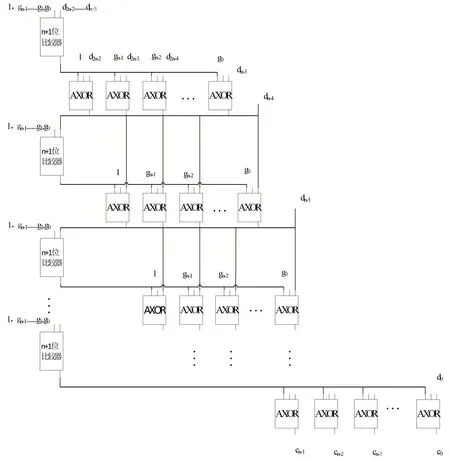
图3模既约除法器

图4 AXOR模块内部结构
4 结果仿真
根据前面文章对二进制域运算的设计与分析,二进制域运算核心是模加和模乘,使用Vivado 2017.4针对Xilinx Artix-7的FPGA设计模加和模乘RTL代码,完成功能仿真。选用NIST推荐的K-163曲线,其二进制域为GF(2163),既约多项式为g(x)=x163+x7+x6+x3+1,实现163位操作数的运算[7]。
模加:随机选取两个163位二进制数其十六进制表示如下:
A=163’
H6ced3df50d18ec55f1513da742ae2e2e287b40312
B=163’
H0e23aa6c3ede1026160969ccb8abd37e4725df218
运算结果C如图5所示。
C=163’
H62ce979933c6fc73e758546bfa05fd506f5e9f10a

图5模加仿真图
模乘:随机选取两个163位二进制数其十六进制表示如下:
A=163’
H6ced3df50d18ec55f1513da742ae2e2e287b40312
B=163’
H0e23aa6c3ede1026160969ccb8abd37e4725df218
运算结果C如图6所示。
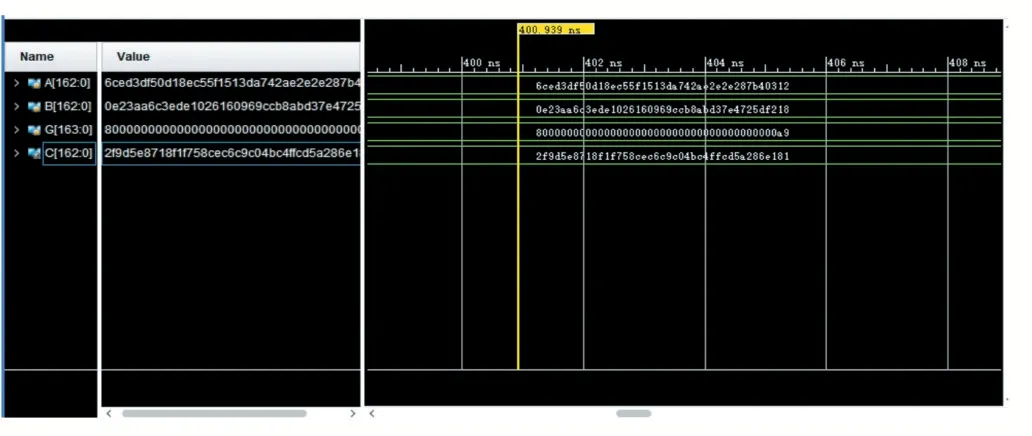
图6模乘仿真图
C=163’
H2f9d5e8718f1f758cec6c9c04bc4ffcd5a286e181
5 结语
本文主要介绍对椭圆曲线密码体制中二进制有限域上的运算设计与实现。本文从硬件编程角度设计出模既约除法器,并给出了一种较为简单的实现方法。二进制有限域上的运算是椭圆曲线密码体制的重要方面,实现二进制有限域上的运算为椭圆曲线运算层和密码协议层奠定基础。接下来的研究工作是优化运算模块的设计及提高模乘运算的效率,实现参数可调整的椭圆曲线密码系统设计。
