跨季节内蓄冰圆筒装置数学模型及应用分析

李艺群，黄凯良，关敬轩，张雪萍，孙晓宇

（1.沈阳建筑大学，沈阳 110168；2.中国建筑东北设计研究院有限公司，沈阳 110168）

0 引言

跨季节冰蓄冷即利用冬季的自然冷量蓄冰后，在夏季融冰释冷，以在降低制冰成本的同时降低建筑能耗。我国东北地区气候严寒，自然冷能储备丰富，跨季节冰蓄冷技术具有较为广阔的应用前景。早在古希腊、伊朗和我国商周时期［1-2］，人们便开始收集冬季天然冰储存于冰窖，用于冷藏食物和夏季的皇宫降温。跨季节冰蓄冷技术的发展主要经历了3 个阶段：（1）初始应用时期，储冰方式以地窖、冰井为主，冷能主要用于炎热天气时食物的保鲜和农产品的贮藏；（2）在电制冷剂发展迅猛时期，跨季节冰蓄冷技术的研究和开发停滞；（3）现如今，因其节能减排的特性，该技术的研究重新引起了国内外的重视，现已在建筑空调、工农业，冷链物流［3-5］等方面有所应用，而如何得到并蓄存冷量已成为研究的重点问题之一。在实际工程应用中，冷量的来源主要分为人工制冰和自然冰雪蓄冷，后者多受自然条件的制约，故本文的主要研究对象为用于人工制冰的内蓄冰圆筒装置。

在人工制冰装置的研究方面，邓广发等［6］率先使用计算机编程，对1190A、ET-60A 等不同型号的蓄冰桶进行模拟，并与实验数据相对比，发现数值模拟可以较好的描述不同运行模式下的蓄冰桶的工作情况。杨自强等［7］采用热平衡方程式建立了内融冰蓄冰桶的数学模型，邹同华等［8］后建立了基于导热微分方程的数学模型，使数值模拟的结果更为精确。石文星［9］已对跨季节冰蓄冷系统的实际应用展开了研究，采用季节性蓄冰和夜间蓄冷系统相结合的运行策略。现有大部分蓄冰桶均设有螺旋管等盘管装置，且均选用乙二醇等作为制冷剂。基于上述分析及研究现状，本文提出并建立了无盘管式的蓄冰圆筒模型，旨在分析并得到装置容积的最优参考值以及蓄冰过程的影响因素，以便于在工程实践中大致选择该技术的适用地区。

1 模型的描述

1.1 物理模型

蓄冰装置的主要分类有冰盘管式、容积式、冰片滑落式和冰晶式［10］，前两种应用较为广泛。而本文则选取的内蓄冰圆筒作为蓄冰装置，将自然冷风视为低温冷媒，当其流经内管时可与管外的水进行热交换，使之相变成冰，储存起来以实现自然冷能在冬夏两季的调用。在冷风流动的过程中，传热将分为多个阶段：发生在管壁表面的对流换热，以及管壁、冰层、水体的导热。

结构模型如图1～3 所示。

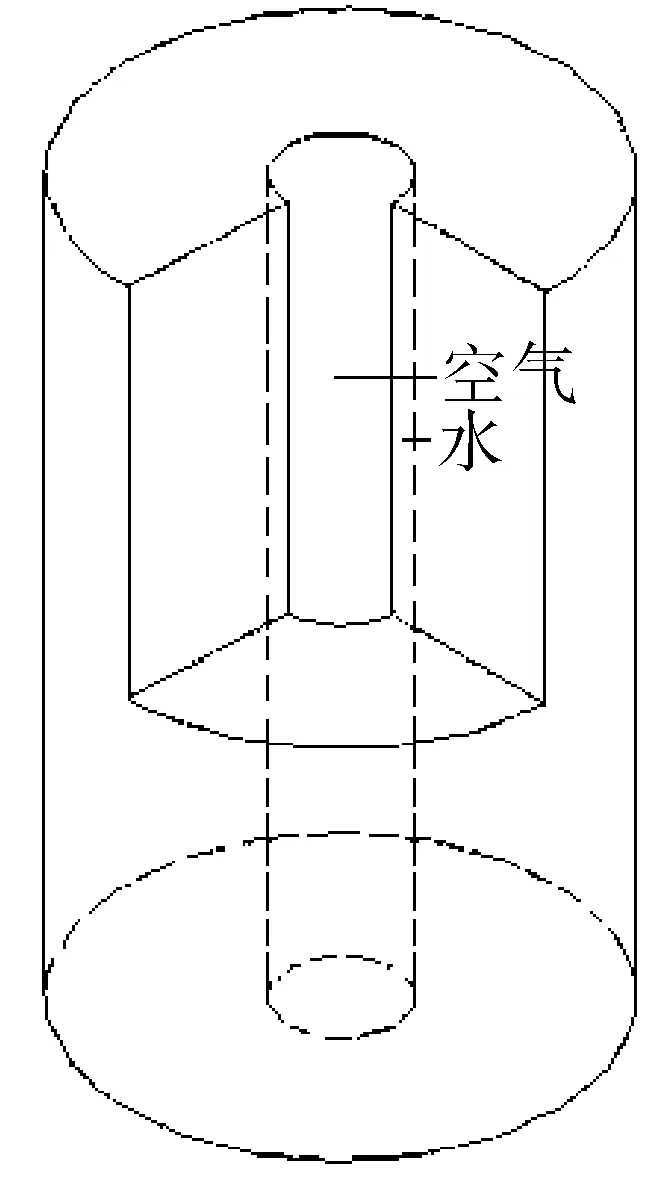
图1 蓄冰桶装置模型

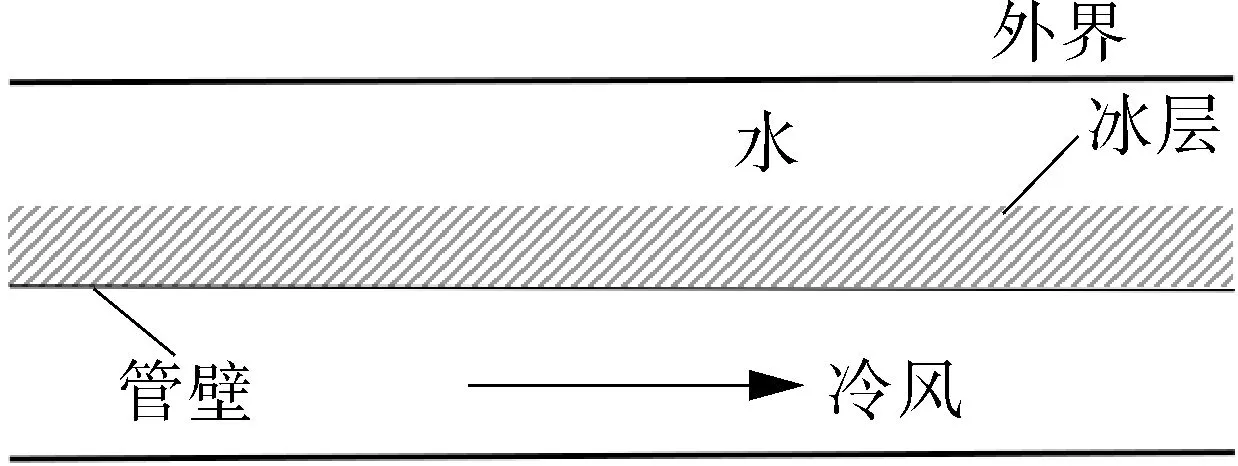
图2 水平轴向界面

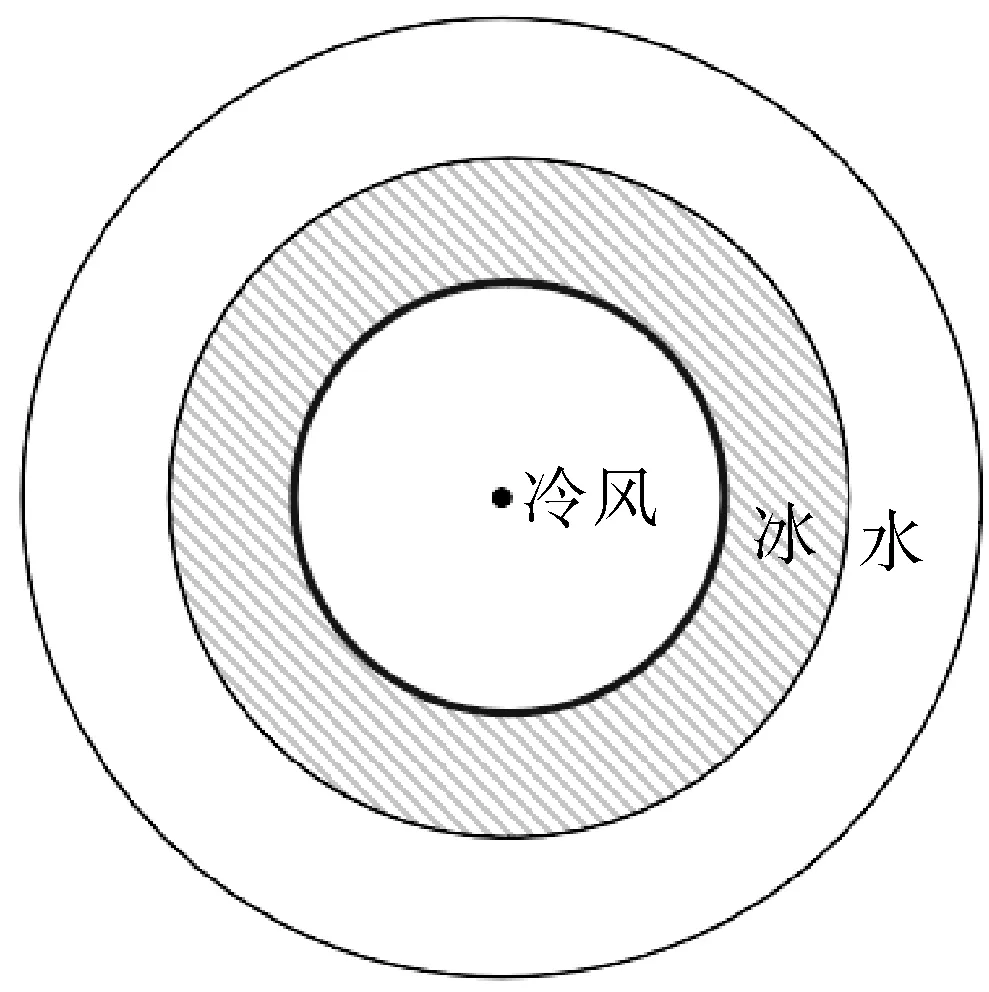
图3 径向截面

而实际的传热过程为径向和轴向的三维导热问题，初始条件、边界条件和几何条件等较为复杂，多采用数值模拟的方法进行求解。常用的模拟方法有焓法、准稳态法、奇异摄动法等［11］，本文采用焓法，将焓和温度一起作为待求函数，从而将液相和固相作整体考虑。为便于求解，对过程做简化如下：

（1）水在相变过程中密度的变化忽略不计；

（2）相界面的温度为水的冰点温度且保持 不变；

（3）将水视为静止，即忽略水对流换热；

（4）各物质导热均匀；

（5）圆管长度有限，流体增加的温度可忽略不计；

（6）在最冷月完成蓄冰，没有冷量损失。

1.2 数学模型

1.2.1 微分方程的确定

圆柱坐标系（r，φ，z）下，传热过程的微分方 程为：

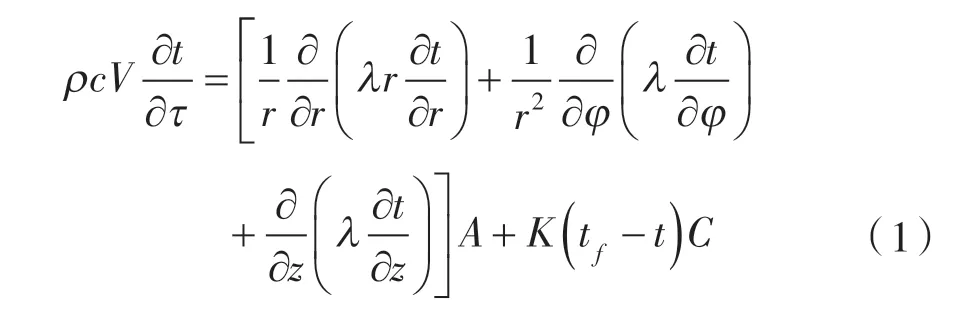
其中 ρ ——材料的密度，kg/m3；

c ——相变材料的比热容，J/（kg·K）；

V —— 相变材料的体积，m3，因截取微元作为研究对象，故长度可忽略，即A ≈V；

τ ——时间；

λ ——导热系数；

A ——相变材料的横截面积，m2；

K ——对流换热系数，W/（m2·K）；

tf——冷媒温度，K；

C ——管道的周长，m。

本文采用焓法，即将温度和焓一起作为代求参数，从而可以简化对相变界面的追踪问题。而其相态则可由焓值h 判定，故所得焓法微分方 程为：

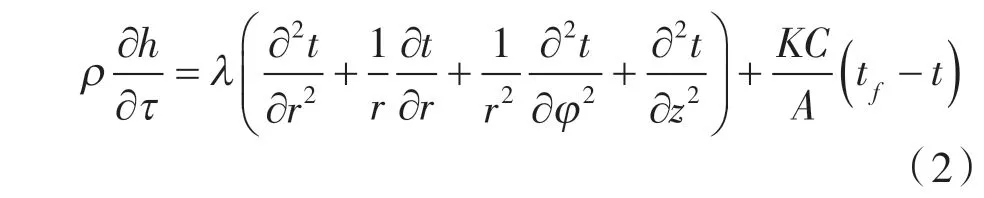
对微分方程进行无量纲处理。

无量纲焓：

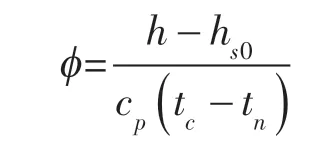
式中 cp——比热容；

tc——相变温度，℃；

tn——管壁温度，℃；

0，s ——下标，饱和状态、固体。

无量纲温度：

无量纲固相表面半径：

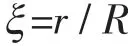
式中 R ——管道的外径，m。

得到无量纲方程为：

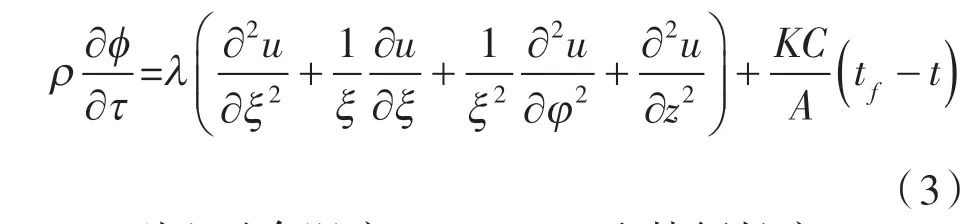
引入过余温度θ=t∞-t=tf-t 和特征长度L=C/A，得到：

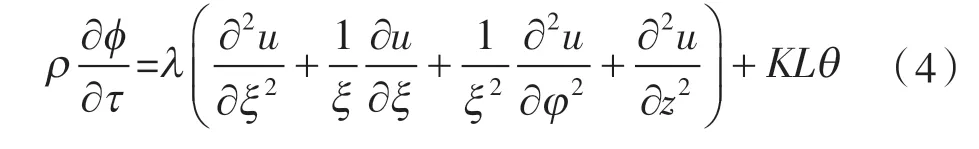
根据假设仅考虑径向导热，则化简得：

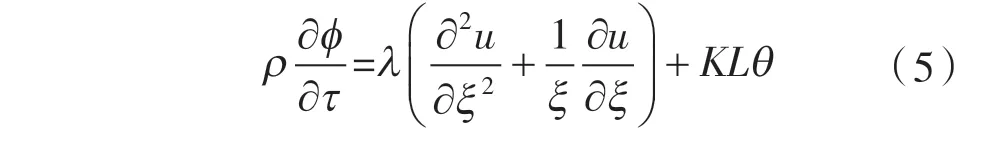
初始条件：

边界条件：

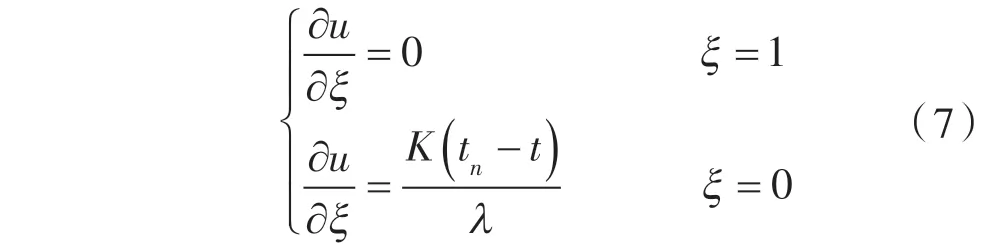
1.2.2 对流换热系数的求解

雷诺数的计算公式为：

放冷工况：

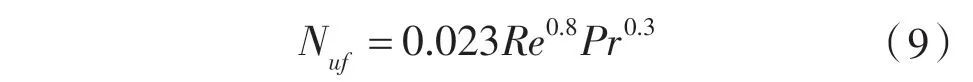
整理得：

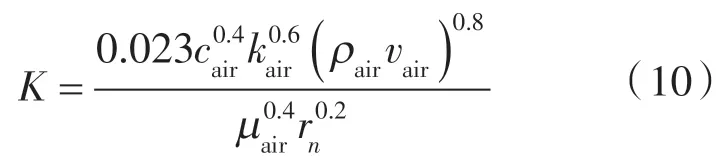
式中 cair——空气比热容，J/（kg·K）；

kair——空气导热系数，W/（m2·K）；

ρair——空气密度，kg/m3；

vair——空气流速，m/s；

μair——空气的动力黏度，Pa/s；

rn——圆筒内径，m。

2 模拟工况的求解及可靠性检验

2.1 模拟工况的求解

本文研究的装置为管内通冷风，管外蓄冰。首先对控制方程进行离散化，本文采用有限差分法，空间变量采用中心差分，时间变量采用向后 差分。

无量纲方程离散后［12-13］：

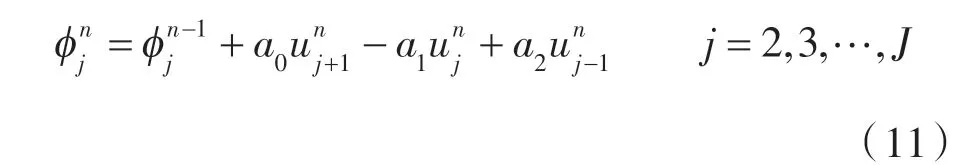
其中无量纲温度的取值由以下条件判定：

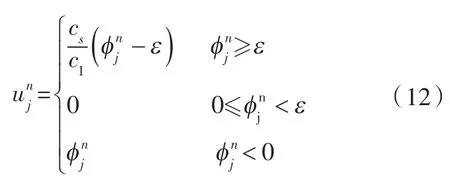
式中 ε ——水的相变潜热。

本文研究的主要问题如下：（1）设定值相同的情况下，每个城市蓄冰量和蓄冰时间的关系；（2）不同装置的初始温度下，蓄冰量和时间的关系；（3）不同城市气象条件下，比较各气象参数对蓄冰过程的影响程度，得出不同城市的蓄冰装置最佳容积。

在模拟的过程中，选取空间步长Δr=1 mm，设定空气流过的内管管径Dn=0.15 m 一定，仅通过改变外管管径Dw对装置容积进行控制，设内外径之差为ΔD。不同城市的参数有诸多不同，本文仅选取了平均温度和风速两个直接产生影响的参数进行分析，根据中国气象统计数据可得，6 个城市在30 年内的平均气象数据如表1 所示。

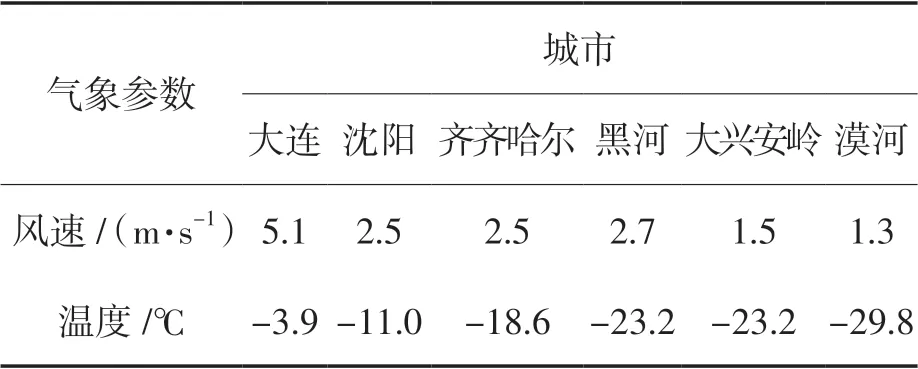
表1 城市平均气象参数

在确定初始值后，进行迭代求解再将前一时刻的值作为初始值，判断无量纲温度的取值，将作为判断相变的条件，从而对微分方程式进行求解，得到所求量。迭代流程见图4。

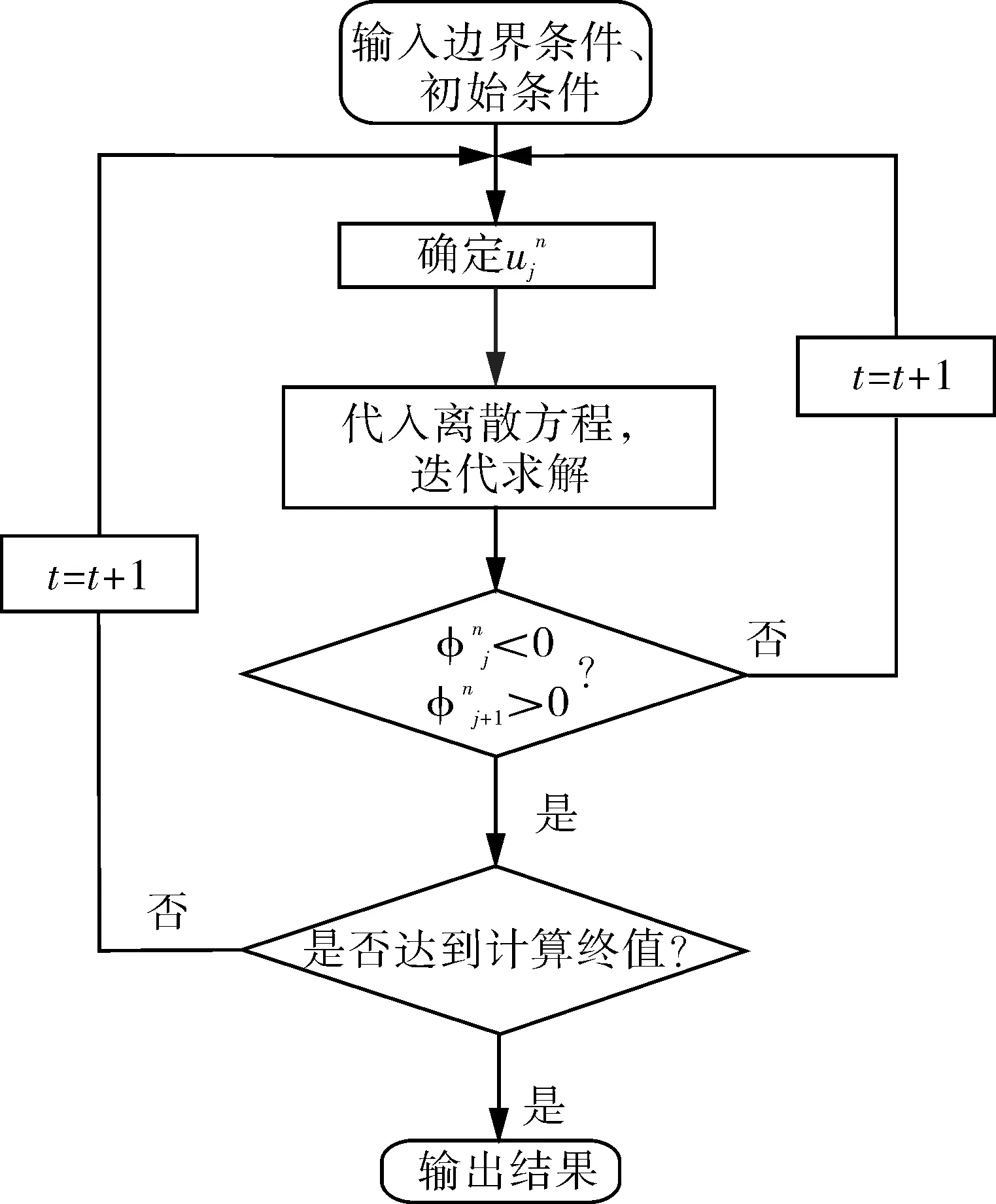
图4 迭代流程

2.2 模型的可靠性检验

本文创新性的提出了内蓄冰圆筒装置，所选取的数学模型曾用于模拟蓄冰盘管的结冰状 态［14-26］，并将模拟结果与试验数据进行比较，结果如图5 所示。

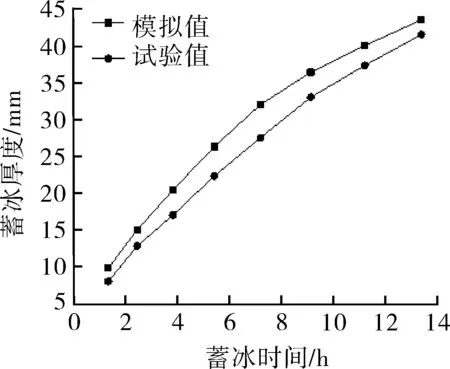
图5 试验和模拟值的比较

模拟结果和试验结果的变化趋势大致相同，而在相同蓄冰时间的情况下，模拟蓄冰量将多于试验值，可能原因为模拟条件为理想绝热，没有与外界产生的热量交换，且假设水体保持静止，忽略了自然对流的影响，考虑的影响因素较少从而导致模拟结果偏离真实值。此外，二者前期差值较大，后期差值逐渐减小，在设定的蓄冰时间段内，模拟值的RMES 为32.2 mm，试验值则为29.2 mm。且随着时间的延长，模拟值和试验值的差距将逐渐缩小，低于误差精度要求，可用于工程实践。因此，将该模型用于对圆筒进行模拟具有可靠性和科学性。

3 数值模拟结果及讨论

3.1 蓄冰装置最佳容积分析

设定的蓄冰时间的不同将导致不同的蓄冰量，从而对装置容积产生了不同的要求。容积过小，多余的冷量将会产生过冷度，容积过大则冰不能完全冻结，因此确定装置的最佳容积成为工程中的重点问题之一。为此，分别对六个城市进行数值模拟，以求得不同蓄冰时间所对应的最佳装置容积。经模拟可得，蓄冰时间和蓄冰量的曲线关系保持一致，故仅选取沈阳作为典型城市进行具体分析，关系如图6 所示出。

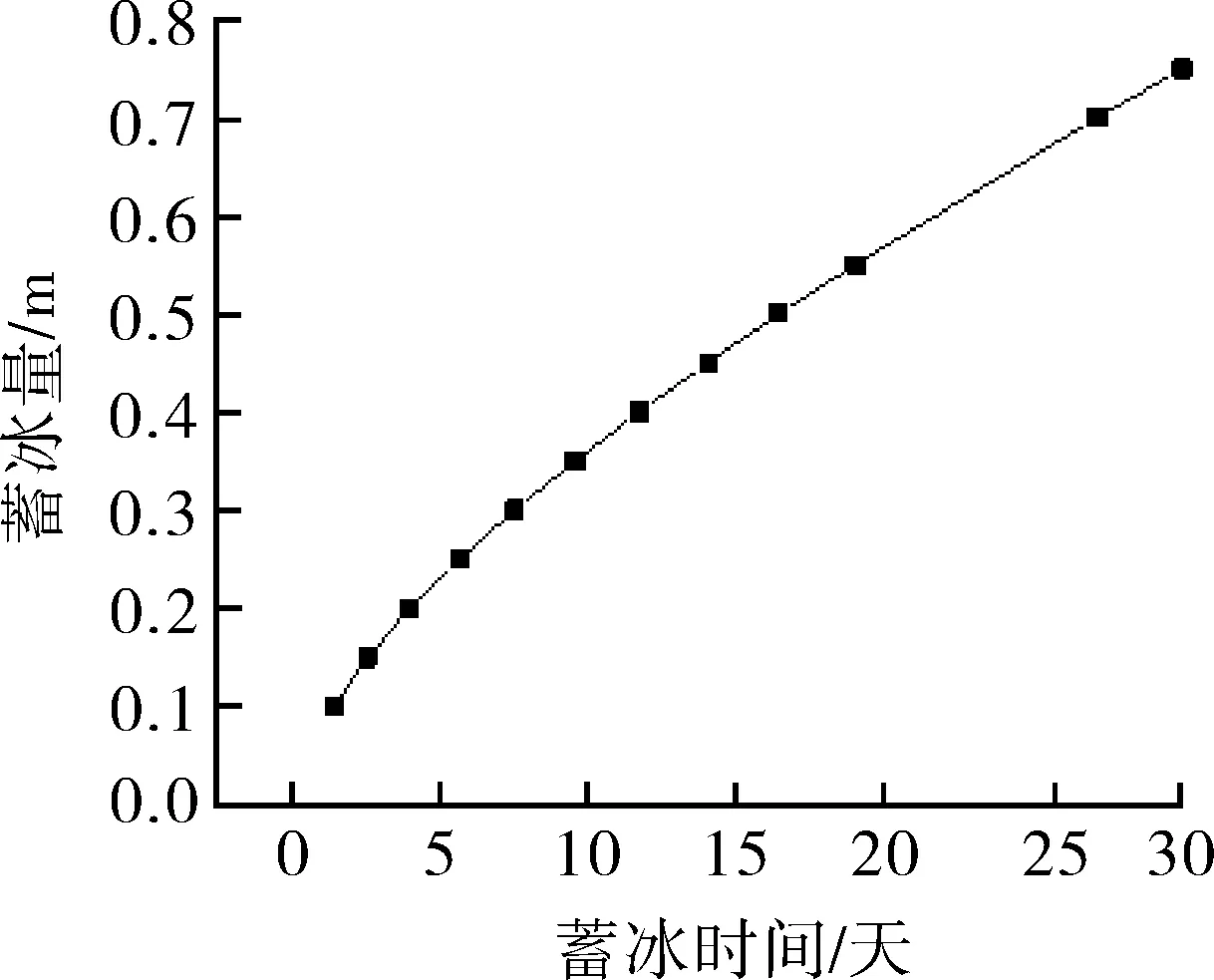
图6 蓄冰量随时间的变化

（1）在相同时间间隔内，蓄冰量的增加率随时间的增加而减小，即结冰速率随冰量的增加而减慢。这一趋势与实际情况相符，说明所构建的数学模型具有一定准确性。由于忽略水在相变过程中产生的自然对流的影响，在蓄冰后期模拟结果将略小于实际情况。

（2）为实现对任意时间点的蓄冰量的计算，通过拟合得到表示蓄冰量和时间的函数关系式。不同类别的函数拟合优度R2的值如表2 所示，经过比较，幂函数结构简单且拟合效果好，可以较为精确地对该函数关系进行描述。

表2 拟合度比较

（3）在上述基础上，若要求在最冷月内完成蓄冰，则代入设定时间31 天，即得装置的最佳蓄冰容积为，外径Dw=0.92 m，厚度ΔD=0.77 m。

3.2 不同初始温度下蓄冰时间的变化

仍选取沈阳为研究对象，比较装置处于3，5，7，9 ℃下的蓄冰时间变化趋势，结果如图7 所示。

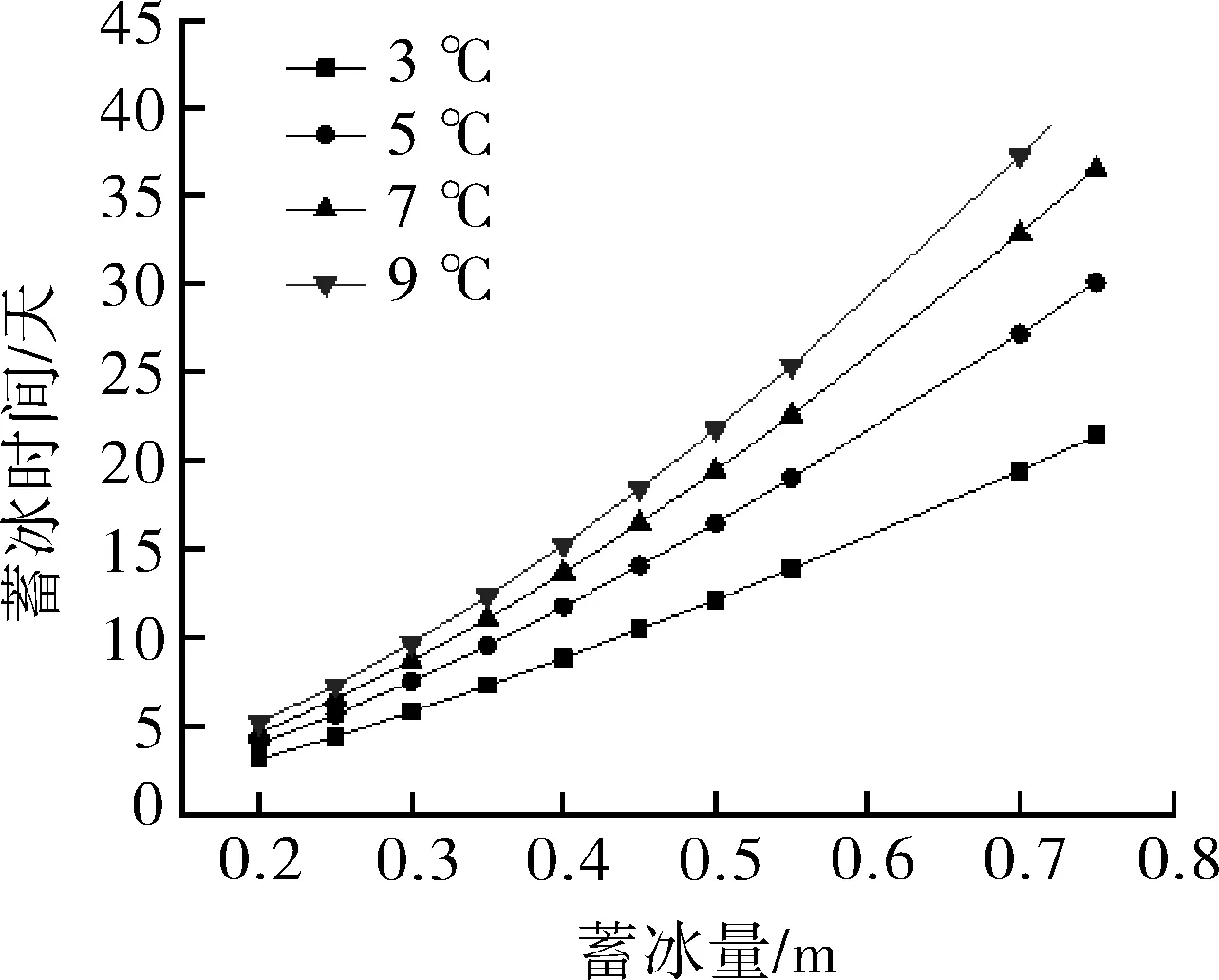
图7 不同初始温度下蓄冰时间

不同温度下的变化趋势大致相同，从图可得，随冰层加厚，蓄冰时间仍以幂函数的形式增加。这一规律在装置初始温度较低时有很好体现，随着温度的逐渐升高，在蓄冰量一定时，相邻温度下的蓄冰完成时间的间隔逐渐变大。同样可以得到，随着初始温度的升高，每两个相邻温度的时间差值却随之逐渐减小，即初始温度为3 ℃时所用的蓄冰时间与5 ℃的差距要大于5 ℃和7 ℃所用的蓄冰时间之差，以此类推，也就是说温度的变化对完全蓄冰时间产生的影响在逐渐减小。

3.3 不同城市的蓄冰装置比较

在不同城市气象条件下，给定蓄冰装置ΔD= 0.2 m，其他条件均保持不变，完成相同蓄冰量时，所用蓄冰时间的计算结果如图8 所示；此外，依次计算每个城市的最冷月最佳装置容积，结果如图9 所示。

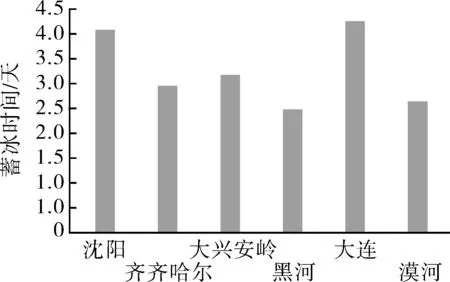
图8 不同城市的蓄冰时间

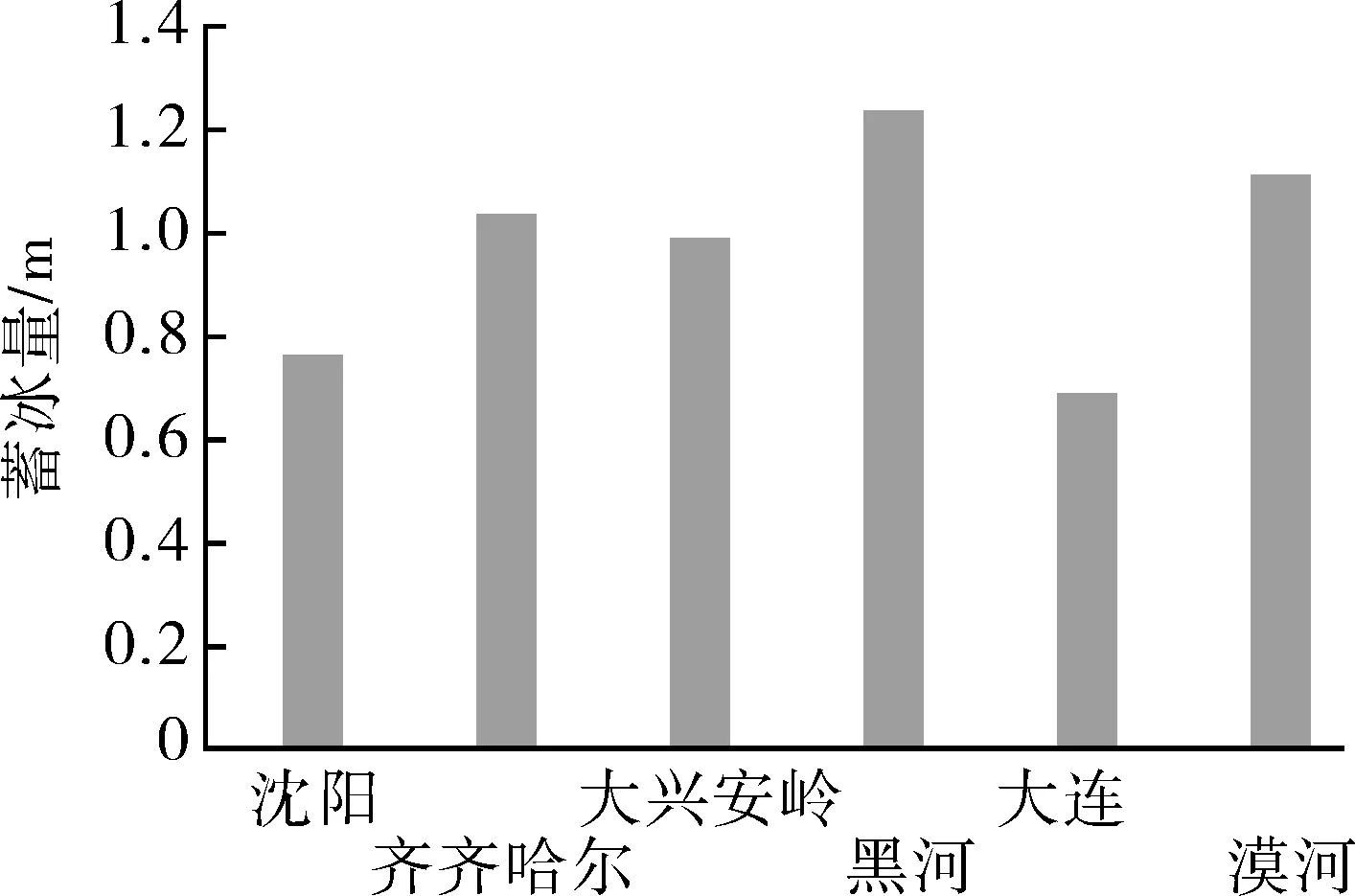
图9 不同城市的最佳蓄冰量

在本文选取的6 个城市中，沈阳与齐齐哈尔的冬季平均风速相同，平均温度不同；大兴安岭与黑河的平均温度相同，风速不同；大连和漠河则是风速极大和温度极低的两种极端情况。通过对以上几组城市进行分析，可得出以下结论。

（1）比较可得高风速和低温均有利于蓄冰的进行。风速和对流换热系数呈正比，风速越大，相同时间冷风代入的冷量增多。高风速可以缩短蓄冰时间并增加蓄冰厚度，低温也可以产生同样的影响。较低的冷风温度，可以使桶内的各点温度降低，增大温差，加强传热，故在条件允许的情况下，选址应尽可能处于高风速和低温的环境之中。

（2）可以分别得出室外温度和风速对蓄冰过程的影响程度。在蓄冰前期，装置容积一定的情况下，室外温度每升高1 ℃，完成蓄冰所用时间将延长0.15 天，风速每提高1 m/s，时间将缩短0.57 天，大连的风速为漠河的3.9 倍，温度为0.13 倍，蓄冰所用时间比漠河延长1.5 天，因风速和温度之间没有具体的衡量指标，故仅从倍数关系来看，每提高1 ℃产生的影响大于风速加速1 m/s。

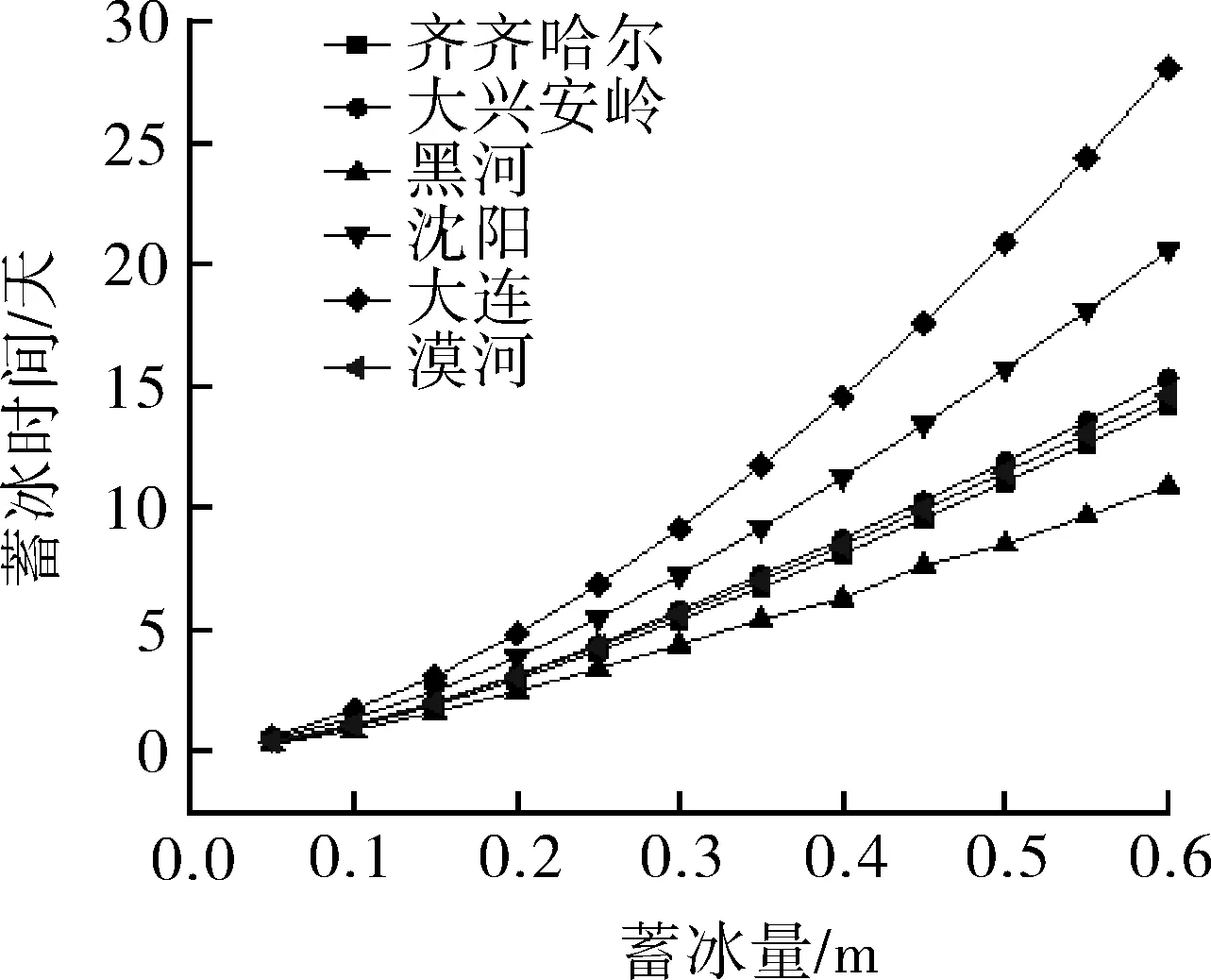
图10 6 个城市的蓄冰时间随蓄冰量的变化

（3）由图10 可得，在温度、风速均不相同的情况下，大兴安岭、漠河、齐齐哈尔3 个城市的曲线却基本保持一致。可得蓄冰过程为风速和温度综合作用下的结果。在二者均不相等时， 蓄冰前期主要受风速的影响，后期受温度的影响，因前期处于显热蓄热阶段，后期处于潜热蓄热即桶内导热阶段，此时的主要推动力为温差，对其蓄冰结果的预测必须从两方面进行综合考虑。

4 结论

（1）由蓄冰时间和蓄冰量的关系可得，蓄冰速率随蓄冰过程的不断进行而减慢。蓄冰时间与蓄冰量的关系可以通过幂函数很好的拟合，从而得到两者变化规律的函数关系式。由此，在沈阳市的气象条件下，若假设在最冷月内完成蓄冰，当内径为0.15 m 时，计算可得最佳装置尺寸为外径0.92 m。

（2）在不同的装置初始温度下，厚度和时间的关系曲线趋势基本一致，且当初始温度呈等额增加时，每两个相邻温度状态下，完成相同蓄冰量所用的蓄冰时间差值越小。

（3）从6 个城市的结果比较来看，蓄冰量和蓄冰时间受风速和室外温度的综合影响，蓄冰前期，高风速更有利于蓄冰过程的进行，蓄冰后期，低温的影响更显著。由此可得，适宜推广冰蓄冷的城市应在确保室外低温的情况下，保证一定的风速，从而尽可能缩短蓄冰时间，减少工程造价。

我国东北地区自然冷能丰富且春秋季较短，大部城市均适宜跨季节冰蓄冷技术的推广和应用。对于此类夏热冬冷地区，实现冷量的两季调用对充分利用电力设施、节能减排、降低能耗具有积极意义，故应结合当地的实际气象条件，充分利用自然资源，积极推动跨季节冰蓄冷技术在工农业、冷链物流、舒适性住宅等方面的实际应用。