非完整移动机械臂的自适应模糊滑模控制研究*

郑耿峰

(福建省特种设备检验研究院，福建 福州 350008)

0 引 言

移动机械臂通常由移动平台和机械臂构成。对于非完整移动机械臂，其移动平台受非完整约束，所以移动机械臂是非完整系统[1]。移动机械臂既具有移动平台的机动性，又具有机械臂的操作灵活性，因此其应用前景广阔[2-3]。

由于系统的高度非线性和强耦合性，并且在实际应用中，系统会受到外界干扰及参数不确定的影响，给系统的控制带来困难。从控制目标的角度，移动机械臂的控制主要可分为轨迹跟踪和点镇定两类。其中，轨迹跟踪最具有实际意义，因而得到了国内外学者的十分关注。文献[4]研究移动机械臂末端与地面接触时的状态镇定，给出了避免翻车的控制策略；文献[5]基于微分平坦方法动态规划运动轨迹，实现了移动机械臂的动力学轨迹跟踪；文献[6]将移动机械臂分解为轮式移动平台和两连杆平面移动机械臂两部分，独立设计轨迹跟踪控制器。

上述研究仅考虑了系统的理想模型，但在系统受到外界干扰或精度要求较高的场合，其适用性有限。近年来，包含不确定性的移动机械臂系统轨迹跟踪控制问题成为研究热点。文献[7]基于滑模控制，设计了可变性轮式移动机械臂的鲁棒姿态镇定控制器；文献[8]针对存在不确定性和干扰的全向轮式移动机械臂，提出了基于鲁棒神经网络的滑模轨迹跟踪控制器；文献[9]提出了采用一种自适应递归神经网络轨迹控制器，处理未建模的移动机械臂系统；陈杰等[10]设计了一种结合模糊控制和非奇异终端滑模控制的六轴臂履带式移动机械臂轨迹跟踪控制器；董玉明等[11]研究了非完整移动机械臂的自适应滑模轨迹跟踪控制，且不需要不确定性的上界信息。

本文针对包含动力学系统不确定性的双独立驱动四轮两连杆移动机械臂，提出一种结合自适应模糊控制和滑模控制的轨迹跟踪控制器。

1 移动机械臂的运动学和动力学模型

典型的移动机械臂由四轮非完整移动平台和二连杆机械臂构成，后两轮采用独立执行器驱动，同侧两轮通过内部连接可同步转动，如图1所示。

图1 四轮二连杆移动机械臂

根据拉格朗日方程和罗兹动力学方程，并考虑移动平台与连杆之间的耦合关系，可得其运动学和动力学方程[12]：

(1)

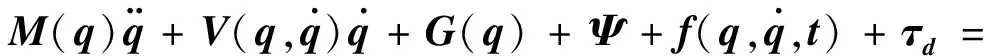
(2)

为了消除式(2)中的拉格朗日乘子项约束力项，考虑非完整轮式移动机械臂系统的零空间特性，有：

A(q)S(q)=0

(3)

(4)

(5)

2 控制器设计与稳定性分析

本文设计模糊自适应滑模控制器，使得移动机械臂系统可跟踪给定的期望轨迹，消除系统不确定性的影响。

控制器结构图如图2所示。

图2 控制器结构图

借助于Lyapunov稳定性分析框架和反演设计方法，本文控制器设计按以下步骤进行。

首先将跟踪误差定义为：

e1=x1-r

(6)

式中：r—给定参考轨迹。

定义虚拟控制量为：

(7)

式中：c1—对角正定常数矩阵，c1∈R4×4。

定义虚拟误差为：

e2=x2-α

(8)

选择正定Lyapunuv函数为：

(9)

对式(9)求导，并将式(6～8)代入可得：

(10)

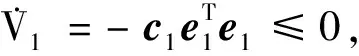
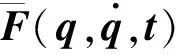
模糊逻辑控制系统是由模糊化、模糊规则库、模糊推理机制和反模糊化4部分组成，其中，模糊系统的规则用如下If-then语句来描述：

采用乘积推理机、单值模糊器和中心平均解模糊器，则模糊系统的输出为：

(11)

式(11)可改写为：

F(x)=ξTθ

(12)

向量ζ的第i个元素为：

(13)

定义最优参数为：

θ*=argmin[sup|f*(x)-F*|]

(14)

式中：F*—待逼近函数。

定义最小逼近误差为：

(15)

本文使用自适应律来确定一个调节机理，让参数误差绝对值达到最小，从而减小逼近误差，即：

(16)

进一步引入滑模控制，定义正定Lyapunuv函数为：

(17)

式中：βi—正的常数；s—滑模面。

s定义为：

s=λe1+e2

(18)

式中：λ—正定常数矩阵，λ∈R4×4。

对式(18)求导，并将式(5)代入得：

(19)

由性质1和性质2可知：

(20)

(21)

对式(17)求导，并将式(16，19～21)代入可得：

(22)

其中：

(23)

将模糊系统逼近项式(15)，并代入式(22)有：

(24)

ε=[ε1ε2ε3ε4]T。

假设1：|ε1|≤Ω，Ω为正的常数。设计模糊系统参数自适应律如下：

(25)

为了减小滑模抖振现象，使用指数趋近律，即：

(26)

式中：ρ，k—正常数对角矩阵。

设计模糊滑模控制器为：

(27)

定理：对于给定不确定非完整移动机械臂系统(5)，满足假设1条件下，则控制器(27)和自适应律(26)可以使得闭环系统是渐进稳定的。

证明：将求导后的式(16，26)代入式(24)，可得到：

(28)

合理选取ki，使得：

ki≥Ω

(29)

(30)

由此可见系统是稳定的。进一步分析其渐进稳定性，定义新项为：

(31)

由式(18)可知，s的值完全由e1和e2决定，于是有：

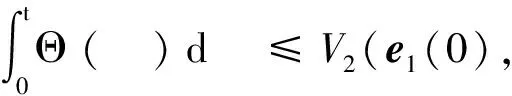
(32)

(33)

由式(17)可知，V2(e1(0),e2(0))为有界，V2(e1(t),e2(t))为有界非增，因此有：

(34)

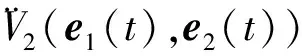
(35)

式(35)表明，闭环系统是渐进收敛的。由e1定义可得，x1将渐近收敛到期望轨迹r。

经过模糊系统逼近总体不确定项后，逼近误差已经较小，因此假设1的条件并不苛刻。而通过设计足够多规则的模糊系统(即N足够大)，可使得逼近误差εi充分小，因此，很容易选择满足式(29)的ki值。

3 仿真实验及结果分析

本文采用Matlab/Simulink，对图1的移动机械臂进行仿真实验。

仿真实验Simulink主程序如图3所示。

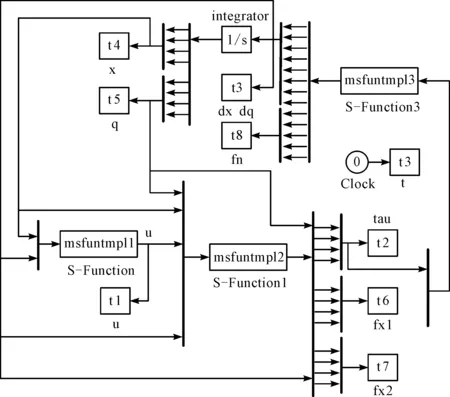
图3 仿真实验simulink主程序

图3中，主程序先由s函数msfuntmpl1输出参考轨迹u，并将数据存于工作空间中的变量t1中，然后将参考轨迹和移动机械臂的当前位置，输入到模糊控制s函数msfuntmpl2中；s函数输出的控制力矩被保存于工作空间中的变量t2中，并将控制力矩作为被控对象s函数msfuntmpl3的输入，最终s函数将输出移动机械臂的速度信息，并将数据存于工作空间中的变量t3中；对移动机械臂的速度信息作积分，可以得到其位置信息，并将其保存于工作空间中的变量t4中；最后综合工作空间数据，求取轨迹跟踪误差、控制力矩输入和自适应模糊控制输出等。动力学模型中各个矩阵与文献[13]中的定义相同。

在仿真实验中，取参考轨迹为：xcd=0.2t，ycd=0.05sin(2t)+0.2t；xAd=0.2t，yAd=0.1sin(2t)+0.2t+0.15。

假设总体的不确定性为：

移动机械臂初始位姿取：

移动机械臂的相关参数设置如表1所示。

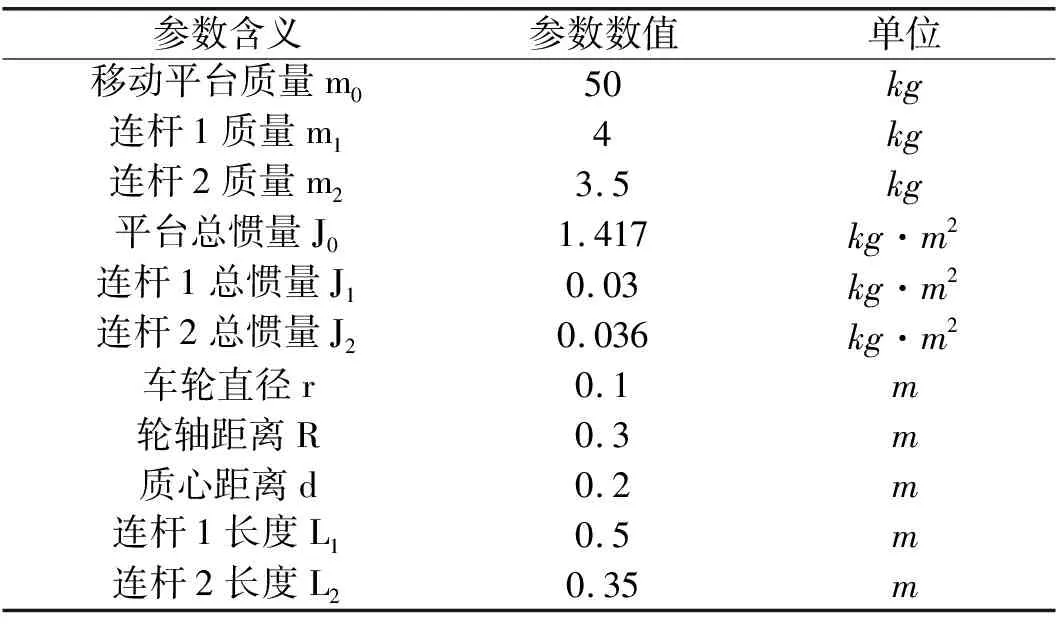
表1 移动机械臂结构参数设置

模糊自适应滑模控制器参数取：λ=diag(14,14,14,14)，ρ=diag(8,8,8,8)，c1=diag(4,4,4,4)，βi=50，ki=20。

定义模糊系统的输入、输出的模糊集合均为{NB, NS,ZO,PS,PB}，对应的模糊变量分别为{负大，负小，零，正小，正大}。各模糊集合对应的隶属函数分别为：

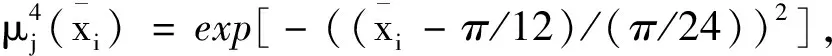
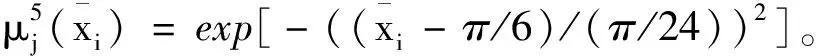
本文首先使用不包含模糊系统的滑模控制器进行轨迹跟踪实验。仅滑模控制器的轨迹跟踪情况如图4所示。

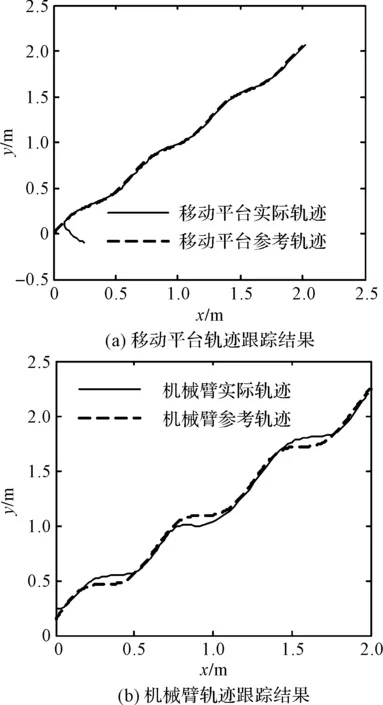
图4 仅滑模控制器的轨迹跟踪情况

由图4知，一般滑模控制器无法完全消除系统不确定性带来的不利影响，因此轨迹跟踪误差较大。

文中控制器轨迹跟踪情况如图5所示。

图5 本研究中控制器轨迹跟踪情况

由图5知：控制器取得了较好的控制效果，移动机械臂的姿态跟踪误差较小，且响应速度快，控制输入变化也较为平稳。可见，通过将自适应模糊补偿和滑模鲁棒抑制相结合，可以有效抵御系统复杂时变动力学参数不确定性和外界干扰，提高移动机械臂在复杂环境下的应用能力。

4 结束语

针对由四轮移动平台和二连杆机械臂构成的非完整系统，考虑其动力系统模型不确定性和外界扰动，本文设计了基于反演法且联合滑模控制、自适应模糊控制的复合控制器。该控制器利用自适应模糊控制最优逼近系统未知不确定性，采用滑模控制对逼近误差进行进一步抑制，提高了系统受复杂不确定性影响下的控制性能。

仿真结果表明：与常规鲁棒控制器相比，在存在复杂时变多变量不确定性时，该控制器仍能精确地跟踪参考轨迹，且控制输入平稳、响应速度快、鲁棒性好和适应性强，可以满足复杂场合下移动机械臂的轨迹跟踪应用需求。