复杂人体运动冗余控制的肌肉协同理论研究进展与展望
2020-03-04彭玉鑫郝增明
杨 毅,彭玉鑫,郝增明,刘 宇,王 新,王 健
(1.浙江大学 教育学院,浙江 杭州 310028;2.上海体育学院,上海 200438;3.沈阳体育学院,辽宁 沈阳 110102;4.浙江大学 运动科学与健康工程研究所,浙江 杭州 310028;5.浙江大学 心理科学研究中心,浙江 杭州 310028)
人类的运动行为(如站立、走、跑、跳等)有赖于自身运动控制。控制运动的神经结构从低级到高级依次分为脊髓、脑干下行系统和大脑皮层运动区3个层级,各层级功能分工不同。神经科学方面的研究表明,运动控制是中枢神经系统(central nervous system,CNS)以层级和并行方式协同处理实现的。运动控制的中心问题是CNS如何产生实现各种行为目标所需的肌肉活动模式。人类个体是开放的复杂巨系统(钱学森等,1990),运动时大脑必须处理一个由大约107个神经纤维、600块肌肉和200个关节等组成的神经肌肉骨骼系统,这导致在神经、肌肉和关节空间可形成的自由度(degree of freedom,DOF)数量n远超过运动所在空间的维数m(m<n)。因此,无论是人体的单一肢体运动,还是整体运动,其运动控制都极具冗余控制的特征(林辉杰等,2012;王爱文等,2017;Hirashima et al.,2016;Latash,2012;Latash et al.,2002)。这种人体运动的冗余控制(redundancy control)问题,也称“Bernstein问题”、多自由度问题。
针对复杂人体运动的冗余控制问题,Winter(2009)提出神经肌肉骨骼系统的四层整合理论(Neuro-musculoskeletal integration):第1层整合是对α运动神经元的所有兴奋/抑制输入的神经求和;第2层整合是指对肌肉内所有募集的运动单元求和,形成肌腱张力;第3层整合是各个关节轴上所有主动肌和拮抗肌的肌肉力矩进行求和;第4层被认为是协同层,通过整合2个或多个关节处各肌肉力矩,共同协调实现动作任务。这种整合、协调过程称为“协同”(synergy)。该理论认为肌肉力矩是CNS控制实现特定任务的最终特征,如支撑力矩(the support moment)可用于量化行走过程中下肢所募集肌肉的激活模式(Winter,1980)。另外,在人体运动的神经肌肉控制机制方面,Bernstein(1967)首次提出一种模块化控制理论,认为层级控制的运动系统包含一组离散的低层级元素结构——运动协同(movement synergies)。大脑明确地将真正的协同作用储存在特定的神经回路中,这些神经回路的联合作用产生对肌肉有任务效率的运动输入,由此可以减少因冗余控制问题引起的计算成本。这种在运动时协同作用的低层级元素结构,在肌肉活动这一层次被称为肌肉协同(muscle synergies)。
个体感知周围环境,结合自身认知解析任务需求,最终选择和执行一系列动作以完成目标任务。具体的运动行为是个体、任务和环境3因素相互作用产生的,为了使运动按预期进行,CNS不仅需要指定大量的输出变量,还必须考虑对运动执行施加的各种生物力学要求或约束(华安珂 等,2019;刘宇,2010;王楚婕 等,2013;王健等,2017;王开元 等,2018)。而肌肉协同是在CNS中编码还是由于任务约束而被激活,目前对于这种肌肉协同的起源是否是神经性起源问题还存有争议。虽然有针对动物,如青蛙(Bizzi et al.,2008;D’Avella et al.,2005)、老鼠(Tresch et al.,1999)和猫(Desrochers et al.,2019;Ting et al.,2007)等和人类(Chvatal et al.,2013)的研究都为肌肉协同理论神经起源提供了直接的生理学证据,但有部分与肌肉协同神经性起源观点相矛盾的实验对这一理论提出了挑战(Kutch et al.,2008;Valero-Cuevas et al.,2009)。Kutch等(2008)利用运动系统信号相关噪声特性来估计产生微小指尖力期间的肌肉激活,然后通过检查不同作用力方向的可变性的形状估算潜在的肌肉募集程度。其研究结果表明,完成该任务是独立募集单个肌肉,而不是通过肌肉协同同时募集多个肌肉来实现。对这类支持肌肉协同假说的实验进行批评的主要观点在于肌肉协同反映任务约束,而不是反映了神经控制策略。随着表面肌电图(surface electromyography,sEMG)和功能性磁共振成像(functional magnetic resonance imaging,fMRI)数据分析的发展,当前结论倾向于将肌肉协同认为是存在于大脑和脊髓中的时空成分,从而支持其神经性起源观点。每个个体都可能使用不同的肌肉激活模式来达到相同的任务目标。基于肌肉协同理论的研究表明不同个体的运动存在一种共同的模块化神经控制机制——肌肉协同。肌肉协同理论可以很好地解释CNS对肌肉的控制机制,从而揭示神经系统的内在功能模式。近年来,国内外学者对肌肉协同理论及其应用的研究越来越多(Cheng et al.,2019;Israely et al.,2018;Singh et al.,2018),本研究就国内外肌肉协同理论的研究进展及其在体育科学、临床医学和机器人控制方面的应用进行综述,以期深刻认识和理解肌肉协同理论,并展望其未来研究和应用的发展趋势。
1 肌肉协同理论
复杂人体运动的冗余控制问题或者多自由度问题,目前主要提出了3个主要理论。
1)消除理论(elimination theory)。该理论认为CNS通过将DOF数量减少到执行任务所需的数量来解决问题(Latash et al.,2007)。这种对DOF的“冻结”源自Bernstein提出的假设,在当代人类运动行为的研究中经常被引用。消除DOF的概念主要是在运动学层面上提出的,而未考虑力量、肌肉、运动单元或多关节任务中的冗余。
2)最优化理论(optimization theory)。其基本思想来源于数学和工程学。最优化是一种通过考虑成本函数中包含的附加条件,在无限种可能性中选择最优解的方法。最优化理论通常被认为是指大脑不断地为它所面临的每一个运动任务计算全局最优(Berret et al.,2019)。研究者们通常依靠计算机进行数学运算来构造最佳的运动指令。这类研究的限制性在于他们只关注优化计算的最终结果,而没有解决大脑如何实现优化的问题。最优化理论有助于理解“为什么”某些动作会比其他动作最终被执行,但它并不能说明大脑实际上是如何触发该最优策略的。因此,大脑是如何选择一个使运动消耗成本最小化的解决方案,对该问题的理解尚不明确。
3)肌肉协同理论(muscle synergies theory)。该理论是一种模块化控制理论,通常认为层级控制的运动系统包含一组离散的低层级元素结构,可以减少由冗余控制问题引起的计算成本。这种低层级元素结构可被称为运动模块(motor modules)、运动原语(motor primitives),或在研究肌肉活动特征时,被称为肌肉协同。大脑明确地将真正的协同作用储存在特定的神经回路中,这些神经回路的联合作用产生对肌肉有任务效率的运动输入。该理论从生物力学分析角度来看,肌肉协同作用过程中,肌肉收缩产生人体多环节链运动时的肌肉力矩。然后,CNS通过整合互动力矩(interactive torque)、重力矩和接触力矩等,精妙准确地进行关节间动力学耦合控制(dynamic cou‐pling)(Zajac et al.,1989),从而优美地完成既定运动目标(孙宇亮,2014)。例如,在上肢的运动协同控制方面,针对绘画任务中关节力矩和肌肉活动的研究表明,肩关节运动由该处的肌肉力矩驱动,而肘关节运动由肩关节处产生的互动力矩驱动,肌肉力矩仅负责调控互动力矩,由位于该关节的肌肉主动收缩来完成(Dounskaia et al.,2002)。另外,在下肢的运动协同控制方面,研究者们通过构建短跑时下肢的基于环节角的环节互动动力学模型,分析了小腿角加速度在髋、膝和足关节处的互动力矩(Hunter et al.,2004)。国内研究者在此基础上的研究表明,支撑期和摆动期时,强壮的股后肌群在这些关节处产生的肌肉力矩在整合、控制外力矩和互动力矩时十分重要(魏书涛 等,2010;Huang et al.,2013;Liu et al.,2017)。为完成目标活动任务,进行关节间动力学耦合控制,要求各相关肌肉群进行协同控制。因此,肌肉协同理论可较好揭示这一复杂运动过程的CNS冗余控制机制。
在人体的运动控制领域,对人体进行的从整体运动到某肢体运动的各种层面上的描述,都会涉及冗余控制的问题。Bernstein在1967年提出以肌肉群的概念解释CNS在维持身体姿势中的冗余控制问题。在过去的几十年里,对人类和动物运动的研究积累了大量证据来支持神经肌肉骨骼系统模块化控制概念(Alessandro et al.,2013;Bizzi et al.,2008;Flash et al.,2005)。CNS 通过结合相对较少的特定空间和/或时间的肌肉活动模式(即肌肉协同)生成必要的肌肉收缩模式来实现目标任务行为(Chiovetto et al.,2013;D’Avella et al.,2003)。
不同学者对肌肉协同给出了不同定义。Safavynia等(2011)认为,肌肉协同代表一个子运动任务库,神经系统可灵活结合其中的子运动任务来产生复杂而自然的运动。某个运动子任务(即肌肉协同)定义了身体各部分执行该任务所需的各肌肉共同激活的固定比例。D’Avella等(2003)认为,肌肉协同是能被下行神经控制信号调制的骨骼肌组合。具体来说,CNS通过某种线性组合的方式激活若干个具有不同功能性的模块化协同结构来完成复杂运动行为,这些协同结构的绝对激活水平由下行神经信号调控(Ting et al.,2007)。肌肉协同被认为是由CNS募集,通过灵活调控各肌肉收缩以完成各种日常行为动作的最小单位。综上,肌肉协同是可被下行神经信号调制,具有时间-空间固有激活特征的一组肌肉组合,是人体层级运动控制的基本控制单元。
1.1 肌肉协同降维特征
肌肉协同是CNS控制下可实现灵活控制以完成日常运动行为的由若干个肌肉组合。这种模块化的控制方式是解决Bernstein问题的有效途径,在人和动物的实验研究以及计算机模拟研究中得到证实。Berniker等(2009)建立了低维控制器模型,证明了降维控制策略可以在不影响结果表现的情况下简化控制过程。
1.2 肌肉协同的功能特征
肌肉协同的功能特征表现在:1)对同一任务,不同肌肉协同会被募集,且各肌肉协同有不同功能。例如,健康成年人手膝爬行时,可在各肢体中分别提取支撑相协同和摆动相协同,前者主要在爬行的支撑相激活,后者主要在摆动相激活(Chen et al.,2017);2)对于不同运动任务,存在功能相似的肌肉协同。D’Avella等(2005)对青蛙在行走、跳跃、游泳运动研究发现,所提取的各个肌肉协同均被调用。肌肉协同自身决定了其功能,并可在不同的运动行为中被调用。Torres-Oviedo等(2006,2007)通过实验发现了其中某个协同对维持静态站姿下的四足间的相对平衡有重要作用。Chvatal等(2013)在研究静态站立受外部干扰时和步行时的肌肉活动时,提取出相似的肌肉协同。Barroso等(2014)从步行试验中提取的肌肉协同作用与骑自行车过程中提取的协同作用相似。完成不同任务时可能会募集相同的肌肉协同,而任务目标的特异性在个别具有特征性的肌肉协同中得到体现(Ting et al.,2007),对于肌肉协同功能特征的理解,有助于更好地理解运动的神经控制机制。
1.3 肌肉协同的增龄效应
在成人运动过程中,躯干和腿部肌肉的肌电活动是由一些与运动模式、方向、速度和身体支撑无关的肌肉协同来解释的(Clark et al.,2010;Ivanenko et al.,2004;Sheynikhov‐ich et al.,2009)。关于肌肉协同的发展也有其他假设:1)成人所固化的肌肉协同模式是从最初大量的运动模式中选择出来的;2)原始模式被抛弃,取而代之的是全新的模式;3)原始模式被保留和调整,而新的模式在成长过程中被添加。很明显,这些假设反映了对神经网络发展过程中的不同约束。为了区分这些可能性,Dominici等(2011)比较了新生儿和学步儿童、学龄前儿童和成人的肌肉协同特征。研究发现,有2个肌肉协同模式在新生儿迈步阶段被保留,而另外2个肌肉协同模式在此阶段之后发展。而对于年轻人与老年人,老年人的肌肉协同特征减少并有所改变(Vernooij et al.,2016)。这也能反映出人类衰老不仅与个别肌肉的变化有关,还与它们之间的协调有关。
1.4 肌肉协同模型分类
肌肉协同通过选择一小部分肌肉来构建可在不同条件下执行任务目标的动作模块。肌肉协同之所以是动作模块,是因为它们反映一组在不同情况下可重复的激活肌肉激活模式。如公式(1)所示,用于将执行各种运动任务时收集的多通道sEMG信号矩阵MX×T,经矩阵分解提取肌肉协同后,包括反映空间特征的协同结构矩阵WX×S和反映时序特征的肌肉激活系数矩阵CS×T(其中X为肌电采集通道数,T为计算样本数量,S为肌肉协同数量,E为残差)。从空间上看,在不同肌肉间,一个WX×S能反映一组肌肉间激活强度关系。从时间上看,一个CS×T能反映一个肌肉协同结构中不同肌肉间的关系是时不变或时变的。根据不同的数学模型与理论假设,公式(1)表示的肌肉协同模型可分为时间型、同步型、时变型和统一型4种。
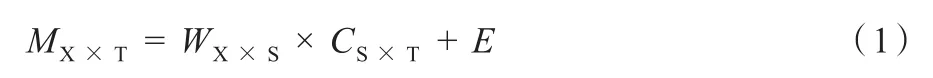
时间型肌肉协同(temporal muscle synergies,TEMMS)的数学模型如公式(2)所示,TEMMS属于时不变协同(time-invariant synergies)(Chiovetto et al.,2010,2012;Do‐minici et al.,2011;Ivanenko et al.,2004)。这里的“时不变”是指肌肉激活系数矩阵ci不随时间变化而变化。ci可通过简单地缩放和叠加在一起来重建每一块肌肉实际活动m(t)。P为时间肌肉协同数量。TEMMS可利用因子分析(factor analysis,FA)方法提取(Ivanenko et al.,2004)。

同步型肌肉协同(synchronous muscle synergies,SYNMS)的是一种时不变、空间固定的肌肉协同。数学模型与TEMMS较为相似,如公式(3)所示,其中N为空间肌肉协同数量,m(t)为在t时刻所采集的sEMG信号,cj(t)为在t时刻第j个协同结构wj中各肌肉的激活系数,e为残差。在协同结构wj中,所有包括的肌肉被同时激活,且相对激活水平不变。各个协同结构中肌肉的激活水平由与之唯一对应的一条肌肉激活曲线cj(t)同步调控(Ting et al.,2012,2015)。

时变型肌肉协同(time-varying muscle synergies,TVAMS)是肌肉激活的内在时间-空间模式,肌肉激活模式由随时间变化的肌肉协同组合产生,也就是说,一组肌肉的协调激活与每一块肌肉的特定时间过程相结合(Bizzi et al.,2008;D’Avella et al.,2005;Dominici et al.,2011;Overduin et al.,2012;Scano et al.,2019)。肌电信号输出由各协同募集时的振幅和时间延迟决定。TVAMS模型如公式(4)所示,其中R为肌肉协同数量,e为残差,wk为第k个协同结构。ck和tk分别为该协同对应的非负缩放系数和时间延迟,其中tk负责调节wk协同结构的激活时序,hk负责控制wk协同结构的激活水平。wk中肌肉间的相对激活水平随时间变化,wk(t-tk)反映第k个协同在其激活起始时刻后(t-tk)处的肌肉激活水平。TVAMS由D’Avella(2003)等首次提出,可利用类似于NMF的方法来提取。
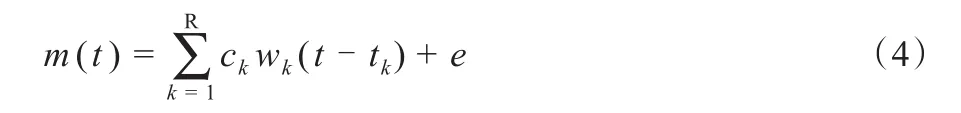
统一型肌肉协同。统一型肌肉协同(unifying muscle synergies,UNFMS),也可称为时间×空间肌肉协同(space by time synergies)模型(Delis et al.,2014;Hinnek‐ens et al.,2020)。时不变和时变UNFMS数学模型如公式(5)、公式(6)所示,单个肌肉模式都可以表示为时间模块wi(t)和空间模块wj的双重线性组合。P和N分别为时间模块和空间模块的数量。cij和tij分别为i时间模块、j空间模块的标量激活系数和时间延迟。神经生理学研究表明,肌肉激活模式可由空间模块或时间模块的肌肉协同模块进行组合产生,这是构成具备统一性UNFMS模型的证据。空间模块对应于所谓的同步、时不变或空间固定协同效应;时间模块对应于所谓的肌肉激活模式、前运动驱动、运动原语或时间固定协同效应。
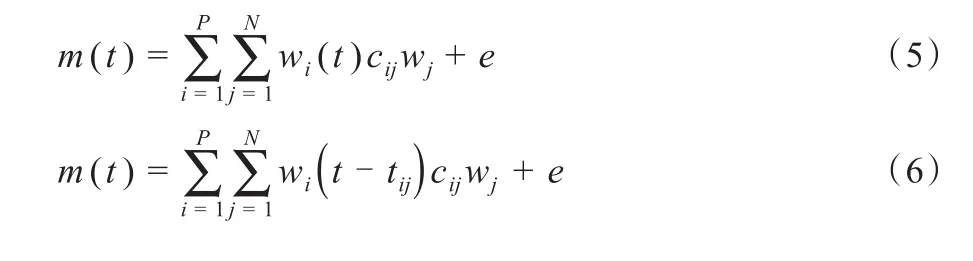
2 肌肉协同分析
肌电信号是深层肌肉活动的生理变化(电信号)直接测量得到的信号活动,能间接反映CNS的运动控制指令。因此,肌肉协同一般从肌肉活动数据中提取。sEMG因其采集时的无创性,使用较为广泛。sEMG肌肉协同分析(图1)通过对完成目标运动任务时肌肉产生的sEMG信号进行矩阵分解来进行,主要过程包括:1)sEMG预处理,目标是利用数字信号处理算法对原始sEMG信号进行预处理,得到归一化包络矩阵;2)肌肉协同提取,目的是将已进行预处理的sEMG信号进行矩阵分解,得到肌肉协同结构矩阵W和协同激活系数矩阵C;3)肌肉协同评价,对在不同变量条件下所提取的肌肉协同模式(协同结构、激活系数)进行相关性分析。
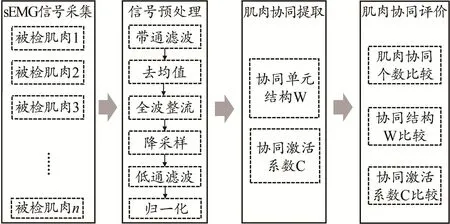
图1 肌肉协同分析流程Figure 1.Procedure of Muscle Synergies Analysis
2.1 sEMG信号预处理
sEMG信号预处理通过在肌肉协同提取前依次经过带通滤波、去均值、全波整流、降采样、低通滤波和归一化等处理得到sEMG包络矩阵。带通滤波和陷波处理可消除漂移、混叠效应和工频干扰。低通滤波和高通滤波可分别消除高频噪声和运动伪影。全波整流用来计算sEMG包络线(Myers et al.,2003)。对经全波整流后的包络线低通滤波,可确保没有高频信号成分改变包络形状,且截止频率越低包络线越平滑。为保证不同对象或肌肉的sEMG同等重要性和处理结果不倾向幅值较大的信号,归一化常利用完成目标任务时的最大自主收缩(maxi‐mum voluntary vontraction,MVC)(Ting et al.,2005)、被检肌肉电信号的峰值或单位方差(Cheung et al.,2012)来计算,最终实现无偏协同提取。降采样利于降低计算成本,加快肌肉协同提取时的迭代收敛过程。Kieliba等(2018)比较了因选择不同归一化方法和带通滤波截止频率参数进行预处理而对肌肉协同提取与被试间相似性(inter-sub‐ject similarity,ISS)的影响,结果表明,无论是采用何种归一化(最大自主收缩MVC或信号自身最大振幅),还是带通滤波器(20~500 Hz或50~500 Hz)都没有显著改变协同权重。然而,归一化可改变一组协同的方差值。通过比较不同的低通滤波器(0.5 Hz、4 Hz、10 Hz、20 Hz)发现,增加低通滤波器的截止频率可以降低由一些肌肉协同的信息重构率(variability accounted for,VAF),并影响个体肌肉的贡献。低通滤波截止频率0.5 Hz时可使包络线极其平滑,并能增强活动肌肉和非活动肌肉的对比。
2.2 矩阵分解方法
肌肉协同提取通过对经预处理后的多通道sEMG信号包络线进行矩阵分解来实现。多通道sEMG信号的肌肉协同结构(空间分布)及其激活系数(时间分布)的估计是一个盲源分离问题,可通过矩阵分解技术来估计基向量集(协同结构)。根据不同数学模型和对协同模块的不同约束假设(如正交性、独立性或非负性),可使用不同的矩阵分解算法来提取肌肉协同模块(Delis et al.,2014)。典型算法有主成分分析(principal component analysis,PCA)(Gorkovenko et al.,2019;Ranganathan et al.,2012)、FA(Ivanenko et al.,2004)、独立成分分析(independent compo‐nent analysis,ICA)(Hyvärinen et al.,2000)、非负矩阵分解(non-negative matrix factorization,NMF)等(Lee et al.,1999;Tresch et al.,2006)。
矩阵分解算法的选择由肌肉协同数学模型和其约束条件来决定。例如,NMF假设待分解原始数据M、协同结构W和激活系数C是非负的。PCA是特征去均值化,使协同作用之间具有正交性。FA假设激活系数不相关。ICA假设激活系数统计独立。然而,多数算法识别非常相似的协同效应。另外,Tresch等(2006)比较了多种不同矩阵分解算法在模拟和实验数据集上的性能,结果表明,PCA在识别肌肉协同上较FA、ICA、NMF效果差得多。ICA对于有恒方差高斯噪声的数据处理效果良好,而当数据有信号相关噪声和协同激活因数相关时受损。NMF相比PCA、FA算法,在数据分析上鲁棒性较好。研究者也通过尝试其他矩阵分解算法来提取肌肉协同。Ebied等(2019)利用张量表征肌肉活动,首次提出一种基于高阶张量分解的肌肉协同提取方法——consTD。Ebied等(2018)提出,二阶盲源识别方法(second-order blind identi‐fication,SOBI)用于评估在腕关节运动分类,并比较PCA、ICA和NMF算法用于对模拟和sEMG实验数据进行肌肉协同提取的性能。结果表明:在没有降维情况下,SOBI比其他3种方法结果更好;在肌电电极数量有限时,SOBI方法更适用,但性能仍显不足。但当采集的肌电信号通道足够多时,NMF表现最佳。总体来说,NMF在生理学上与肌电信号更相关,因为非负值信号能很好地反映肌肉收缩行为(肌肉不能被“负”激活),从而具有更好的解释性,因此被广泛采用。
2.3 肌肉协同评价
2.3.1 肌肉协同数量
在分析不同姿势任务时肌肉协同的差异时,最常用的是比较所提取的肌肉协同数量。确定肌肉协同数量的最主要方法是基于VAF曲线的方法(Allen et al.,2019)。VAF的计算公式如公式(7)所示,其中X、T分别为被检肌肉数量和采样点数量。M为待分解的sEMG包络矩阵,Mcon为所构造矩阵,根据肌肉协同模型不同而不同。VAF参数的取值范围为[0,1]。从矩阵分解角度来讲,肌肉协同数量越多,VAF值越大,表示重构精度越高,即Mcon和M越接近。
基于VAF曲线确定肌肉协同数量的方法,大概可分为 4种:1)VAF阈值法(Torres-Oviedo et al.,2006)。当VAF参数值大于设定阈值时,可认为所分解出肌肉协同矩阵W和C可充分重构原始sEMG信号。用于确定肌肉协同数量时,VAF阈值常设在0.80~0.95 SYNMS(Gizzi et al.,2011;Rodriguez et al.,2013)、0.65~0.80 TVAMS(D’Avella et al.,2005;Overduin et al.,2008)、0.9 左右 TEMMS等。2)VAF曲线趋直法(Cheung,2005)。当协同数目从l开始增加时,VAF斜率变化是一个由初期变化急剧、后期变化缓慢的过程,最后斜率值逐渐趋近于0,这意味着当前所取的肌肉协同数量n对于提升重构原始sEMG的效果不明显。因此,根据VAF曲线近似于直线时判定应提取的协同数目(Cheung et al.,2009;Santuz et al.,2020;Tresch et al.,2006)。3)VAF曲线斜率最大法(Tresch et al.,2006)。选取VAF斜率变换最大时对应的协同数量。4)VAF增量阈值法(Cheung et al.,2009)。选取当协同的提取数量进一步增加时,VAF的增加小于75%时对应的数量。

基于VAF曲线方法因受人体执行目标任务时生物力学条件约束,导致确定协同的准确数量时并没有“金标准”。而且,肌肉协同的提取与数量选择,易受信号噪声的影响,换言之,基于VAF曲线方法,会将噪声引起的肌肉协同被提取出来。因此,有学者利用不同分类算法,如二次判别分析(quadratic siscriminant analysis,QDA)、线性判别分析法(Linear Discriminant Analysis,LDA)、朴素贝叶斯法(naive bayes,NB)和K最近邻(K-Nearest Neighbor,KNN)等和统计检验方法提出自动任务解码算法(Delis et al.,2013),以此选择最佳的肌肉协同数量。
2.3.2 肌肉协同的相似性
为了比较不同任务条件下的肌肉协同差异,通常使用皮尔森相关系数(Pearson’s correlation coefficient)、圆形互相关系数(circular cross-correlation coefficient)来度量不同肌肉协同结构矩阵或激活系数矩阵向量间的相似性(Frère et al.,2012)。皮尔森相关系数计算公式如公式(8)所示,当r>0.9时,即认为具有较强相似性。

3 肌肉协同理论应用
3.1 在体育科学中的应用
基于肌肉协同分析已经在各项体育活动研究中得以应用(Vaz et al.,2016)。了解协同结构中各肌肉的相对激活水平有助于理解运动项目的规律,从而指导训练并降低受伤概率,最终提高运动表现。Matsunaga等(2017)分析了跑步10 min前后的肌肉协同:与之前的研究相似,肌肉协同数量一致;前3个肌肉协同相似,但第4个肌肉协同激活骨盆区域周围肌肉的活动从躯干区域开始,这可能是在脚部撞击时,更容易受伤的原因,因为肌肉协同因长时间跑步而改变,其姿势控制会从躯干转移到下肢。
对于体操项目,Frère等(2012)对9名国家级水平的体操运动员在完成向后大回环动作时的肌肉协同进行了研究,发现前2种肌肉协同在被试之间一致,但第3种协同表现出可变性。第3种协同作用的可变性可能与较低水平的神经控制有关,而与生物力学约束无关。躯干、手臂和肩膀肌肉的协同作用进一步限制了肩关节的伸展,从而降低了受伤的概率。
对于骑行项目,Hug等(2010)研究受过训练的骑行者的下肢肌肉活动,发现9名被试能提出相似的3个肌肉协同。Turpin等(2016,2017)研究了在高强度骑行中使用站立姿势相对于坐姿的优势,结果表明,在下肢肌肉方面,采用2种骑行姿势时的肌肉协同作用结构相似,但功率输出达到600 W时伸肌激活时间存在差异。因此,研究建议只有当功率输出大于600 W时,才能利用站立姿势。至于上肢肌肉,站立时更活跃,所以,即使上肢没有产生能量输出,教练员和运动员也应该训练肢体间的协调性,以提高运动员的成绩。因为协同作用激活系数和肌肉协同向量都能被技能学习所调节,所以,未经过训练的骑行者可以训练自己获得类似的肌肉,以提高运动表现。
对于赛艇项目,Shaharudin等(2014,2016)分析了未受训练的被试分别在滑动型和固定型的划船机上进行划船运动的差异,结果与以往的研究结果一致(Torres-Oviedo et al.,2010),肌肉协同的激活曲线被调节,但其协同结构保持不变。中枢神经系统对肌肉的激活权重分配有所不同,神经系统不断做出调整,以优化肌肉协同完成划船运动,使在滑动型划船机(腿部肌肉)和固定型划船机(背部肌肉)上划桨时减少损伤。研究建议在训练阶段进行肌肉协调性的优化,以提高训练的经济性。
对于冰上曲棍球项目,Kim等(2018)研究了韩国冰球国家队运动员和没有冰上运动或其他专业运动训练经验的健康成年人在平衡受到干扰时肌肉活动的差异。研究发现,在干扰起始阶段,优秀运动员中出现了与头部的控制有关特定肌肉协同。该协同可以反映头部位置突然改变时(如在轻快的加速和减速滑冰中)控制平衡的特殊能力。因此,冰球运动员通过平衡训练,避免了外部干扰而产生受伤的潜在风险。肌肉协同分析为这种训练策略提供了一种量化评价工具。
对于举重项目,Kristiansen等(2016)研究了不同力量训练是否会影响举重运动员和未接受训练对象在卧推时的肌肉协同变异性。经过5周的卧推力量训练后,肌肉协同有一个对象内变异,而那些未接受训练的对象则没有这种变异。根据所获得的结果,肌肉协同的内部组成可以作为评价运动员卧推成绩的一个指标。因此,教练员可以考虑在训练和康复计划中监测肌肉协同的变化,从而合理完善和评估训练内容。
这类研究主要关注肌肉协同分析在运动训练中的应用,此外,肌肉协同理论在人体多关节运动控制仿真中也得到了应用(Ezati et al.,2019)。Meyer等(2016)提出一种基于肌肉协同的神经肌肉骨骼仿真框架来预测中风患者的步行运动。通过建立3种不同模型——肌肉激活控制模型(每条腿35块)、关节扭矩控制模型和肌肉协同控制模型(每条腿5个),对比分析和评估了3种模型在2种速度(0.5 m/s和0.8 m/s)下被试的步行运动学和动力学的能力。研究发现,在0.5 m/s的模型校准速度下,这3种控制方法都能很好地预测受试者的行走运动学和动力学参数;而速度为0.8 m/s时,只有肌肉激活控制模型和肌肉协同控制模型才能很好地预测,且肌肉协同控制模型可以最准确地预测新的步态周期。当预测被试如何以1.1 m/s的速度行走时,肌肉协同控制模型可预测步态周期,并且接近根据步速和步幅之间的线性关系所估算的步态周期。Shourijeh等(2020)为解决步行生物力学仿真中静态优化时,最小化拮抗肌的共激活以及可能的关节僵硬等问题,提出一种协同优化算法(synergy optimization,SynO)。该算法优化估算肌肉激活上的协同结构如何影响步行过程中计算出的下半身关节刚度。随着协同个数从2增加到6时,髋部和膝盖屈曲的最大和平均关节刚度降低,而静态优化算法产生最低的关节刚度值,结果表明,SynO可通过增加肌肉的共同激活作用来增加关节的僵硬度,而且以较少数量的肌肉协同作用行走会导致关节僵硬度增加,甚至可能增加稳定性。
3.2 在临床上的应用
中风、脑瘫、脊髓损伤和帕金森病等患者常伴有运动功能障碍,其主要病因是神经功能障碍。临床上,因为运动过程中的神经活动难以直接测量,所以大多数运动能力评估测试都集中在行为和运动学水平上进行(瓮长水等,2004;尹傲冉 等,2014;Safavynia et al.,2011)。但行为或运动学结果的改变可能是由多种不同的神经功能异常导致。肌肉活动反映了运动神经元活动,因此,对运动功能障碍人群进行肌肉协同分析,有利于识别执行各种任务时的大脑活动变化。Cheung等(2012)研究了不同严重程度中风患者患侧和健侧的手臂肌肉协同特征,揭示了皮质损伤后肌肉协同的3种不同作用模式——保留(preservation)、合并(merging)和分级(fractionation)。在同一患者中可能同时存在2个或所有的肌肉协同作用模式。另外,这些模式与运动功能受损程度和中风后的持续时间有关。对于轻、中度患者,健侧和患侧的肌肉协同属保留模式,尽管激活系数有差异,但协同结构相似;对重度患者,患侧的肌肉协同数量减少,属合并模式。其他学者对中风后亚急性患者步态期间肌肉协同的研究表明,肌肉协同的合并模式是亚急性脑卒中患者的重要标志,运动功能改变并不依赖于肌肉协同的数量,其合并程度与肌肉力量的增加和踝关节角度范围的增加负相关(Hashiguchi et al.,2016)。肌肉协同的分级机制仅在中风多年后的慢性中风患者中发现,患侧的肌肉协同数量较健侧有所增加,而且是健侧肌肉协同的分级。肌肉协同的这种分级机制可增加四肢和肌肉控制的灵活性,弥补中风导致的远端关节运动受损。Steele等(2015)在研究脑瘫患者步态过程时发现,与健康的受试者相比,脑瘫患者肌肉协同数量减少。Fox等(2013)研究了不完全脊髓损伤儿童在完成不同任务活动时的肌肉协同表现,结果发现与健康儿童相比,他们的肌肉协同数量减少。
国内学者也利用肌肉协同分析,在脑瘫、中风患者的临床康复与评价应用上进行了研究(汤璐,2017;Ji et al.,2018)。肌肉协同分析为临床医生提供洞察潜在的神经运动策略和肌肉活动的功能结果。
3.3 在机器人控制方面的应用
受人体姿势控制理论的启发,肌肉协同分析技术在基于 sEMG的实时假肢,如手(Catalano et al.,2014)、上肢(Rasool et al.,2016)、下肢(Afzal et al.,2017)等控制中应用较多(Alessandro et al.,2013),其主要思路是利用肌肉协同分解提取运动意图特征,从而识别目标任务特征。例如,Choi等(2011)使用非负性肌肉协同矩阵,将前臂肌肉活动映射到4个预定义的腕关节运动意图(屈/伸和桡/尺侧活动)。类似地,Jiang等(2014)使用NMF算法提取肌肉协同,随后使用该算法实时获取控制信号控制手腕屈/伸和旋前/旋后。Berniker等(2009)利用肌肉协同和低维模型构建了一个性能接近全维控制器的简化控制器。Rasool等(2016)提出一种基于肌肉协同的任务识别算法(muscle synergy based task discrimination,MSD)控制下臂假肢,通过概率独立成分分析(probabilistic independent component analysis,pICA)来获得特定任务的肌肉协同。然后根据状态空间的过程动力学模型,并结合一个有约束的卡尔曼滤波器来实时估计控制信号。基于肌肉协同理论的在机器人假肢控制,可实现更灵活的动作控制。
4 总结与展望
肌肉协同理论认为复杂人体运动的冗余控制是以肌肉协同为基本单元来进行的,它假定CNS使用少量肌肉协同的灵活组合来激活肌肉。肌肉协同理论的研究已取得较大进展,研究者常通过2种不同方法产生肌肉活动验证肌肉协同假设:1)直接刺激运动系统;2)使人类或动物执行具体目标行为。前者是人为地刺激神经系统中的多个位置,可产生相对较少的肌肉激活模式。一部分对脊椎动物直接刺激其运动系统的研究为肌肉协同理论提供了生理学证据,且另一部分研究通过对行为过程中sEMG的统计分析提取出肌肉协同也可检验这个假设,但这些研究一些证据仍是间接的,难以证伪。有部分与之相矛盾的实验对这一假设提出了挑战,这类研究的主要观点在于肌肉协同反映任务约束,而不能反映CNS的运动控制策略。因此,需要有更能批判性地评估这一假设的实验。
为了验证肌肉协同理论,获得直接证据,未来关于肌肉协同的研究方向有:1)通过设计多样化任务实验范式,营造多自由度的冗余控制环境来验证肌肉协同。实验设计的关键是在足够丰富的行为条件下检查记录的sEMG。肌肉协同可以解释的行为条件的范围越广,这种解释的支持就越多;2)通过理论建模工作来严格检验肌肉协同的模块化假设并评估其潜在的神经起源。肌肉协同理论是一种不同于最优化理论的方法,但并不互相排斥。在肌肉活动中发现的维数减少可能是最优化控制的一种结果,不能归因于严格意义上的神经硬连线协同效应,特别是当肌肉协同是通过对任务执行过程中的sEMG信号进行矩阵分解提取出来时。
