基于灰色理论的主轴箱瞬态环境热误差分析

李志伟

摘 要：基于灰色理论模型突出的非线性拟合功能，本文通过数据的关联度分析法建立动态模型，即可近似任意非线性函数。灰色理论兼备自主学习与建模响应敏捷等特点，针对轮槽铣床主轴箱热误差模型数据处理复杂的特性，具有良好的适用性。结果表明，通过建立灰色理论热误差预测模型，以主轴箱关键温度测点所测温度为依据，确定分析模型的理论输出与系统实际热特性关联度，最终得到预测结果鲁棒性较好的主轴箱热误差。

关键词：主轴箱;灰色理论;瞬态环境;温度测点;热误差分析

中图分类号：TG659文献标识码：A文章编号：1003-5168（2020）34-0021-04

Analysis of Transient Environmental Thermal Error of Headstock Based on Grey Theory

LI Zhiwei

（Sichuan College of Architectural Technology，Deyang Sichuan 618000）

Abstract： Based on the prominent nonlinear fitting function of gray theory model， this paper established a dynamic model through data correlation analysis， which could approximate any nonlinear function. Grey theory combines the characteristics of independent learning and quick modeling response， which has good applicability for the complex data processing characteristics of the thermal error model of the wheel groove milling machine headstock. The results show that by establishing a gray theoretical thermal error prediction model， based on the temperature measured at the key temperature measurement points of the headstock， the correlation between the theoretical output of the analysis model and the actual thermal characteristics of the system is determined， finally， the thermal error of the headstock box with better robustness is obtained.

Keywords： headstock;grey theory;transient environment;temperature measuring point;thermal error analysis

研究發现，设备加工期间，主要发热部件为主轴箱内的电机与主轴系统。主轴箱是机床的重要组成部分，其热误差是机床的主要误差之一。因此，本文将主轴箱作为研究对象，以主轴箱关键温度测点为分析依据，通过建立灰色理论模型GM（1，1）预测主轴箱瞬态环境下的热误差。

1 模型的理论基础及建模原理

设[x0n]为初始测点温度，随机温度测点的初始测点温度函数如式（1）所示，[n]为随机温度测点。

[x0=x01，x02，…，x0n]               （1）

利用灰色理论预测主轴箱热误差时，应利用主轴箱测点温度数据建立GM（1，1）模型。取[x1（0）]作为主轴箱的热误差样本参数序列，[xi（0）]为测点温度函数，[i=2，3，]…。结合序列[ζ0i（n）]，即生成新的预测模型：

[x（0）i=x（0）i（1），x（0）i（2），…，x（0）i（n）]                  （2）

[ξ0i（n）x（0）i（n）=ξ0i（n）j=1nx（0）i（j）]                    （3）

式中，[n]为随机温度测点;[j]为随机温度测点的实时温度值。

利用[ξ0i（n）xi（0）（k）]序列相邻数据的均值，重新构成温度序列：

[t（0）1（k）=0.5ξ01x（0）1（k-1）+0.5x（0）1（k）]，[k=1，2，…，n]       （4）

因此，可建立预测主轴箱热误差的GM（1，1）灰色理论模型：

[x（0）1（k）+αt（0）1（k）=i=2nbix（0）i（k）]                 （5）

式中，[α]为当量发生系数;[bi]为当量灰作用系数。

利用式（5），系数[α]和[bi]构成系数矢量关系：

[QN=α1b1b2…bNT]              （6）

式中，T为转置符号。

也就是说，GM（1，1）预测模型热误差序列组成的单位列向量为：

[PN=x（0）1（1）x（0）1（2）…x（0）1（n）T]          （7）

通过相应完善的热误差及温度序列，构成[N]阶矩阵：

[M=-t（0）1（1）x（0）1（1）…x（0）N（1）-t（0）1（2）x（0）1（2）…x（0）N（2）????-t（0）1（n）x（0）1（n）…x（0）N（n）]                  （8）

利用式（7）和式（8）矩阵变化，得到式（9），其能转换为矩阵方程组。

[yN=MPN]                                 （9）

由函数最小二乘法则，结合式（7），便能计算出模型的系数当量：

PN=（BTB）-1BTyN                           （10）

式中，B为n阶矩阵。

根据式（10）可得，GM（1，1）预测模型的时间响应关系能近似为：

[x∧（1）1（k+1）=x（0）1（1）-1αi=1nbix（0）1（k+1）×exp（-αk）+1αi=1nbix（0）i（k+1）]      （11）

其中，[x（1）1（0）=x（0）1（0）]。

将式（10）得到的系数当量代入式（11），可求出主轴箱的GM（1，1）热误差预测模型[x∧（1）1]：

[x∧（1）1（k+1）=x∧（1）1（k+1）-x∧（1）1（k）]               （12）

2 主轴箱温度测点的选择与优化设计

2.1 主轴箱测点选择

轮槽铣床在常温状态下进行半精加工，此时主轴箱的主轴转速为1 500 r/min，分析该工况下主轴箱瞬态环境的热误差影响，并相应设置测温点，以便及时获取主轴箱的温度及热特性信息，使用的设备主要有涡流位移感应器、Pt100热阻温度感应器及Fluke温度测试系统。为了保证各测点的实效性及准确性，每间隔120 s采集一次数据，主轴箱共设置21个测温点，具体分布如图1所示。

2.2 温度测点优化设计

根据灰色关联度算法对机床温度测点进行分类，通过分析测点的实效性及准确性得到测点的三维时频图，如图2所示。

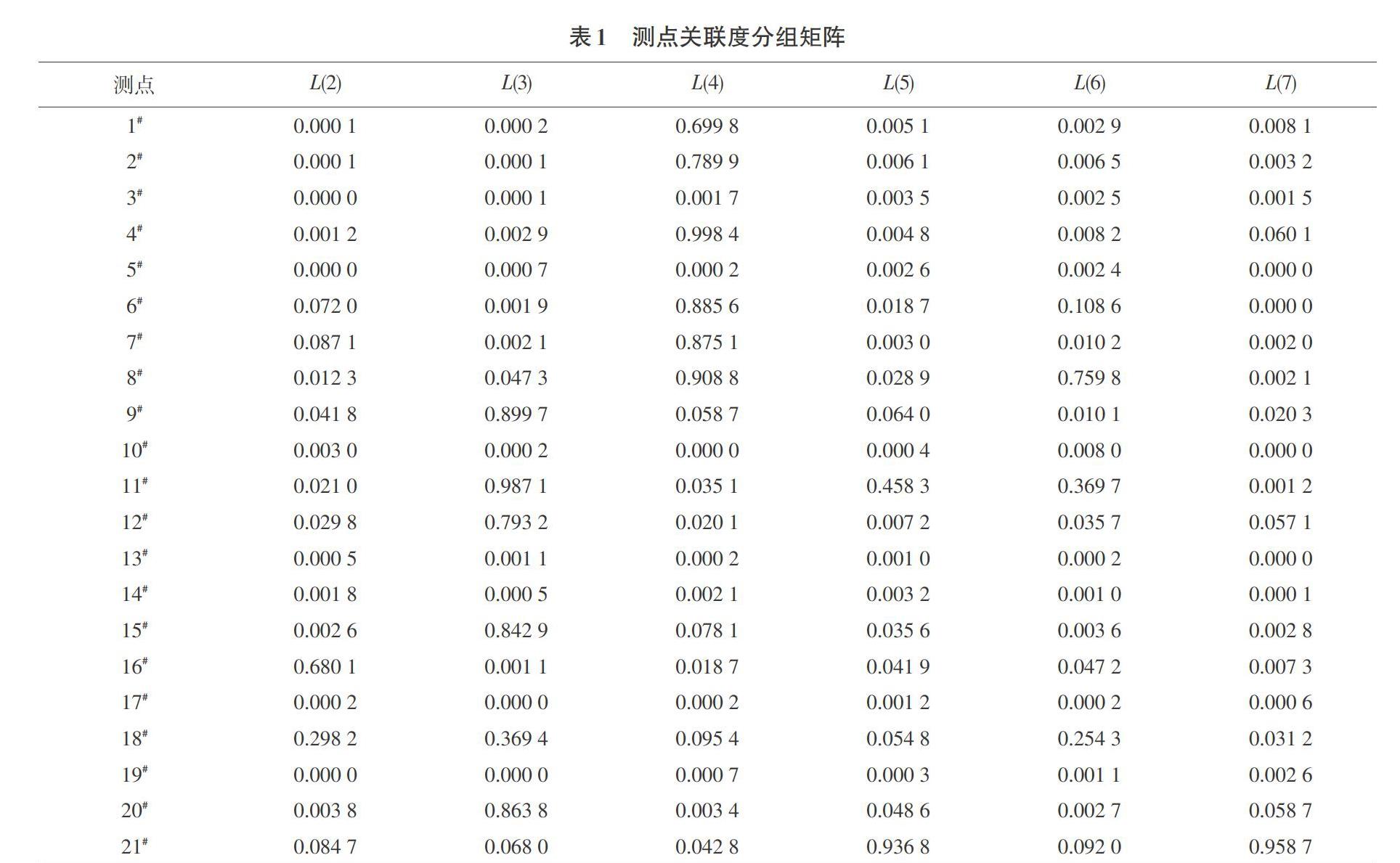
通过时频图分析，各测点温度动态响应有效，能真实反映加工状态测点温度变化，使用灰色关联度对主轴箱测点进行分组优化，当量发生系数取2.5，当量灰作用系数取6时，各测点的动态响应性及准确性较好，则分组函数[L（c）]如下：[L（2）]=265.347，[L（3）]=308.285，[L（4）]=497.012，[L（5）]=806.253，[L（6）]=810.056，[L（7）]=364.128，结果表明[L（6）>L（5）]，且满足[L（6）>L（7）]，结果证实，将测点分6组时，热误差分析结果最佳。

为了保证测点分组的有效性，本研究得出相应测点温度关联度分组矩阵，如表1所示。

由表1测点关联度分组矩阵，将已确定的6组测点进行比较，按照关联度及热误差影响强弱筛选归类，保留对热误差分析有实用价值的测点，具体如下：16#、18#;9#、11#、12#、15#、20#;6#、7#;1#、2#、4#;8#;21#。

利用相关系数法从以上各组中选一个重要测点作为研究对象，根据各组数据间的相关热误差关联度选4#、6#、8#、11#、18#、21#为热误差关键测点，至此将测点总量由21个优化至6个。将6个温度感应器分别安装于主轴箱对应测点位置，并将3个电涡流位移感应器安装于主轴[X]、[Y]、[Z]方向，用于实时监测三个方向的热变形状况，保持机床工作条件不变，连续加工4 h，初始转速设为1 500 r/min，为保证数据的有效性，各测点每间隔120 s采集一次数据。测点温度随主轴转速及时间的增加而升高，其主要原因是主轴长时间工作，本身发热量累计增高。以测点温度数据为基础，对主轴箱三个方向进行热误差分析，主轴在[X]向的热误差平稳变动较小，但在[Z]、[Y]两个方向热误差变化明显，随时间及转速的增加而迅速增加，当主轴达到热平衡时，两个方向的热误差逐步趋于稳定。

3 灰色理论模型预测主轴箱热误差

3.1 预测理论依据

将测点所测[u]个温度分成[u-v]个组，各组含[v+1]个数值（令[v]为响应输入参数，[v+1]为反馈映射）。每组中输入参数的数量，表示前[v]个温度对第[v+1]个温度有关联，为了保证输入参数不失真，同时提高预测有效性，[v]的取值范围一般为6～11。

3.2 具体预测进程

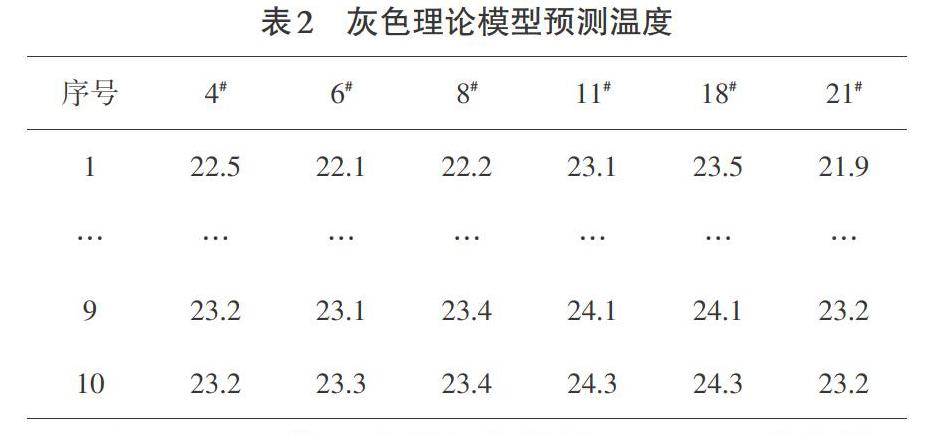
以测点温度关联度为依据，将表1中前10个温度值作为灰色理论预测模型的输入参数，后10个温度作为检验参数。对输入参数做实效性检验后，导入Matlab程序，通过多次模拟训练，预测模型的失效逻辑误差为4.759 18×10-2。考虑到主轴箱实际工作状态、热特性及测点数量，在所有测点不失真的前提下，预测模型能保证这个精度符合要求，预测结果如表2所示。

为能准确预测主轴箱的热误差影响，对上述预测温度进行分析，得到主轴箱在三个方向的热误差，与之前通过各测点温度样本分析得到三个方向的实际热误差进行比较，检验预测模型的准确性，发现预测的结果与实测值近似，如图3所示，详细分析结果如表3所示。

通过上述过程，将实际值与预测分析的结果进行比较，主轴箱热误差在三个方向的极限残差分别为0.042 4、0.007 4、0.022 9，均值残差分别为0.039 5、0.044 4、0.003 0。以上数值均为正，且都小于1，因此利用灰色理论模型对主轴箱热误差的预测能近似反映真实结果。

4 结论

本文使用灰色理论模型预测主轴箱热误差，其间通过在主轴箱设置温度测点来对比分析热误差。结果证明，温度测点实测值与理论模型预测值接近，都能真实反映主轴箱的热误差，因此灰色理论模型具有准确性较好的预测水平，对机械设备的热误差分析具有实用价值，也为机械设备的热特性探索开辟了新的方向。

参考文献：

[1]余治民，刘子建，艾彦迪，等.基于模糊神经控制理论的数控机床热误差建模[J].中国机械工程，2014（25）：2225-2230.

[2]董展飞，马秀红.给子回归分析的故障率顶测模型[J].国外电子测量技术，2005（5）：28-29.

[3]徐国祥.统计顶测和决策[M].上海：上海财经大学出版社，2005：22-23.

[4]罗佑新，张龙庭，李敏.灰色系統理论及其在机械工程中的应用[M].长沙：国防人学出版社，2001：56-57.

[5]王壮民.灰关联分析模型在机械设各评价中的应用[J].山西煤炭，2005（2）：34-35.