基于双协方差随机子空间识别的类噪声数据低频振荡辨识

2020-03-03林伟斌季天瑶张禄亮

广东电力 2020年1期

林伟斌，季天瑶，张禄亮

(华南理工大学电力学院，广东广州 510641)

目前，电网规模不断扩大，系统间的互联程度不断增大，越来越多的高倍率快速励磁装置投入使用，导致系统弱阻尼低频振荡出现概率更高[1-2]，极大地危害电网的稳定性，也限制了互联系统传输容量最大化。因此，监控和分析低频振荡模态参数，对确保电力系统的安全稳定具有重要意义。

低频振荡模态识别方法可以分为基于模型和基于量测信号方法[3]。由于电网结构越来越复杂，基于模型的方法计算复杂，建模困难，会导致出现维数灾等问题，且无法实时计算参数，在实际应用中受到限制。近年来，广域测量系统已在电力系统中大规模使用，为基于量测信号的方法提供了数据支持[4]。基于量测信号的方法无需知道系统结构，可以在线快速准确地识别低频振荡参数，是一种更简单直接的方法。随着电网结构愈加复杂，基于量测信号的方法逐渐成为低频振荡模态识别研究的重点。

根据激励源的不同，量测信号可分为：由明显扰动(如短路故障、投切大负荷)引起的暂态振荡信号和正常运行时负荷随机波动引起的类噪声信号[5]。基于暂态振荡信号的方法可以准确地提取所需的低频振荡模态参数，许多专家也进行了相关研究并取得了良好的结果。采用暂态振荡信号进行低频振荡模态估计最具有代表性的方法是Prony算法，其算法简便，识别结果令人满意，但抗噪性能差，在含噪情况下识别精度差。文献[6]使用了时域和频域混合的方法进行模态识别，该方法与Prony算法相比有更好的抗噪性能和更高的识别精度。此外，基于暂态振荡信号的常用方法包括傅里叶变换[7]、小波变换[8]、希尔伯特-黄变换[9]。虽然基于暂态振荡信号进行低频振荡模态辨识效果良好，但暂态振荡信号发生概率低，难以实时获得，无法实时反映系统状态，难以判断正常运行期间的小干扰稳定性。相反，由负荷波动引起的类噪声信号几乎一直存在，可实时获取。基于类噪声信号的方法可以实时监控系统状态，在发生明显振荡前识别出低频振荡的模态参数，从而实现对弱阻尼或负阻尼的预警，这是电力系统调度运行人员更为关心的，因此该方法在低频振荡的监测中有更好的应用前景。

近年来，基于类噪声信号的低频振荡方法大量涌现，基于随机子空间识别(stochastic subspace identification，SSI)的方法是其中的代表。该方法应用系统的状态方程进行参数估计，能方便直接地从数据中获取状态，算法参数中仅系统的阶次较难确定。为解决模型定阶问题，文献[10]采用稳定图法自动定阶，文献[11]采用经验模态分解(empirical mode decomposition，EMD)与SSI相结合的方法进行模态辨识，文献[12]引入一致性指示值判别真实模态和虚假模态。但上述研究均是基于单一维度下的汉克尔矩阵得到的模态稳定图进行模型定阶。本文提出一种新型的基于SSI的低频振荡模态辨识方法。该方法是在SSI算法的基础上，构造2个不同维度的汉克尔矩阵进行模态辨识，基于2个不同维度的汉克尔矩阵下得到的同阶极点进行匹配而得到超清稳定图，最后再对超清稳定图进行系统聚类，获得最终的真实模态参数。

本文方法不需人工进行定阶，相比于基于单一维度下的SSI方法能更有效地区分真实模态和虚假模态。采用传递函数构造的合成数据以及3机9节点系统仿真数据对本文方法的有效性进行验证，并与传统SSI算法进行对比。

1 基于协方差的SSI算法

由环境激励的自由度离散系统的状态方程为[13]：

(1)

式中：A∈Rn×n为系统的状态矩阵；C∈Rl×n为系统的输入矩阵；xk∈Rn和yk∈Rl分别为系统k时刻的状态量和输出量；wk∈Rn是驱动过程中的白噪声扰动量；vk∈Rl为测量噪声；wk和vk均为不可测量的信号，假设它们为互不相关、均值为零的白噪声平稳序列；n为系统阶数，在本文中为低频振荡模态数；l为系统输出数量。

在离散域中，对状态矩阵A进行特征值分解：

A=ψΛψ-1.

(2)

式中：Λ=diag(λs)，s=1,2,…,n，λs为分解得到的第s个离散模态特征值；ψ为特征矩阵。对应的第s个连续时间特征值λs,c及低频振荡模态参数为：

(3)

(4)

式中：Δt为采样时间间隔；fs为低频振荡模态频率；ξs为低频振荡阻尼比；ωs为低频振荡模态角速度；Re表示取特征值实部。

SSI是一种用于模态参数估计的高效系统识别工具，具有数值简单性和鲁棒性的优点。根据投影矩阵的不同，SSI分为DATA-SSI和协方差驱动的SSI[14]。在保留原有信号的信息的情况下，DATA-SSI采用QR分解对数据量进行压缩，而协方差驱动的SSI采用托普利茨矩阵对数据量进行压缩。在实际运算中，协方差驱动的SSI可采用快速傅里叶变换进行数据压缩，而DATA-SSI采用的是QR分解，运算速度较慢。为了满足快速计算和实时估计低频振荡参数的要求，本文采用协方差驱动的SSI来进行模态参数估计，其数学过程如下[15]。

首先由系统输出量构造汉克尔矩阵：

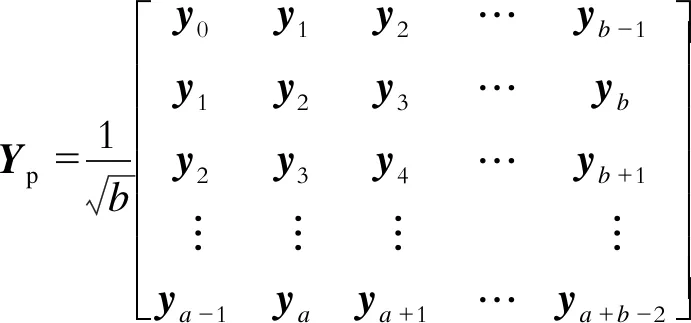
(5)

(6)

(7)

式中a、b分别为汉克尔矩阵的行数和列数。理论上，为满足统计分析的需求，b→，即获得的系统输出量数据越多时，识别结果越准确。但实际中无法做到数据量无穷大，且数据越多计算负担越大。相关文献表明，当a> round (n/l)(round(·)代表向上取整)，且b>20a时，SSI算法的识别结果能满足精度要求。在本文中，为了在计算精度和计算成本之间取得一个较好的平衡，b的取值对应时间长度为10 min的数据。下标“p”表示“过去”，“f”和“f，2”表示“未来”，即Yp为“过去”汉克尔矩阵，Yf和Yf,2为第1和第2个“未来”矩阵。

根据式(5)—(7)构造托普利茨矩阵：

(8)

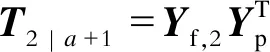
(9)

对式(8)进行奇异值分解，获得奇异值矩阵

(10)

式中：S1、S2为非零奇异值的对角阵；U1、U2及V1、V2分别为左、右单位正交奇异阵。奇异值降序排列，1表示主要信号，2表示噪声信号。

由于wk和vk互不相关，由离散随机状态模型的性质可得

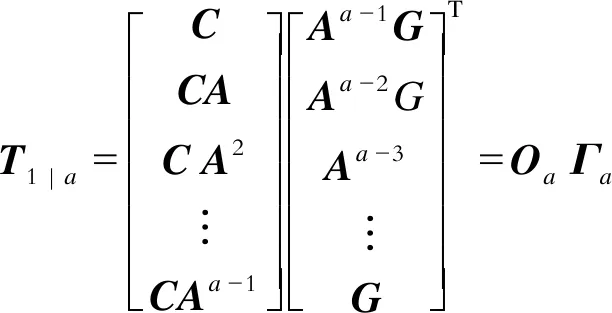
(11)

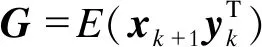
比较式(10)和式(11)可得：

(12)

再由式(11)可得

T2|a+1=OaAΓa.

(13)

将式(12)代入式(13)可得

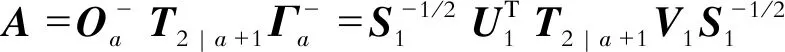
(14)

最后根据式(2)—(4)计算低频振荡模态参数。

2 模态参数自动识别

2.1 基于双协方差汉克尔矩阵的虚假模态剔除法

在不确定系统阶数及噪声干扰的情况下，SSI算法的模态阶数n往往设置得远大于真实模态，以获取所有的模态信息，导致识别结果会包含许多虚假模态。传统的SSI是采用稳定图法，将不同阶数下的分解结果绘制于同一张图中。稳定图的横坐标为频率，纵坐标为模态阶数，相邻两阶次计算的模态参数差值小于设定阈值时，合并为一点，然后依靠经验人工选择稳定点，其稳定点对应的即为真实模态。显然，该方法需要操作员有丰富的经验，操作员的能力对最终模态结果影响很大，无法实现真实模态自动提取。为此，本文提出了基于双协方差的汉克尔矩阵虚假模态剔除法(false model rejection based on double covariance Hankel matrix，FMRDCHM)。

由前述可知，式(5)—(7)中汉克尔矩阵的行a、列b是可变量，不同的a、b取值所获得的模态参数存在较大差异。但试验结果表明，当阶数设置大于真实模态数时，分解结果均包含所有真实模态参数。文献[16]中提到，低频振荡的低阶模态数通常会小于5，即能量占比大的主要模态数会小于5。因此，本文将模态阶数设为50，即可包含所有的低频振荡模态。FMRDCHM的基本原理是不同的汉克尔矩阵分解得到的结果不同，但不同阶次下的虚假极点与物理极点间的距离会大于物理极点与物理极点间的距离，即

|λi,1-λi,2|<|λi,1-λj,2|.

(15)

式中：λi,1为汉克尔矩阵H1的物理极点；λi,2为汉克尔矩阵H2与之对应的物理极点；λj,2为H2的虚假极点。通过试验发现，在迭代过程中，真实模态一直存在且对其的辨识结果保持相对稳定，而由噪声引起的虚假模态的辨识结果波动很大；因此，以极点间的距离判定其是否为虚假极点。若极点间的距离大于1，则判定为虚假极点；反之为物理极点。

极点间的距离

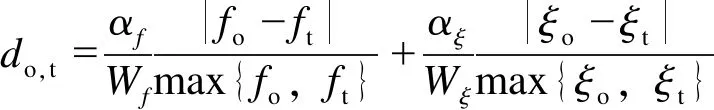
(16)

式中：α为权重；W为容差；f和ξ分别代表频率和阻尼比；下标o、t分别代表基于H1和H2获得的参数。考虑到模态分析中，频率稳定至关重要，是系统稳定的先决因素[17]，因此αf应大于αξ，本文中αf取0.7，αξ取0.3，αf+αξ=1；另一方面，不同阶次下的模态结果中，阻尼比波动远大于频率波动，且频率误差较小，为反映阻尼比和频率间的差异，Wf取值应小于Wξ，本文中Wf、Wξ分别取0.05、0.1。为了减少计算量，可依据低频振荡的模态频率和阻尼比范围，剔除0.1～3 Hz频率范围外和0%～20%阻尼比范围外的模态，再使用FMRDCHM。

FMRDCHM的流程如图1所示，基本步骤如下：①首先根据类噪声数据构造2个行列不同的汉克尔矩阵H1和H2；②采用基于协方差驱动的SSI算法计算，得到2组不同阶次下的模态识别结果，剔除频率在0.1～3 Hz外的极点，剔除阻尼比在0～20%外的极点，将筛选后位于低频振荡模态范围内的2组极点，分别设定为参考组极点和验证组极点；③根据计算同一阶次下极点间距离，在验证组中寻找与参考组对应的最近的极点，若极点间的距离大于1，则判定为虚假极点，剔除该对极点。

2.2 基于系统聚类的物理模态提取

在剔除虚假模态后，进行物理模态参数提取。本文中，为了有效确定模态阶数及模态参数，采用基于系统聚类的物理模态提取算法。

系统聚类是模糊聚类中的常用方法，其基本思想是：先将每个样本独自看成一类，根据所定义类的距离，计算各类中的距离，将距离最小的两类合并成一个新类，如此循环，直至合并的类满足结束条件。本文将合并的结束条件定义为：

min|De|>1，

(17)

DA,B=min{da′,b′|a′∈A,b′∈B}.

(18)

式中：De为第e次迭代计算的距离矩阵；DA,B为类A、B间所有样本间的最短距离；da′,b′表示类A中的样本a′与类B中样本b′间的距离。系统聚类流程如图2所示。

基本步骤如下：

a)初始化：将FMRDCHM筛选得到的q个极点，分成q类，即C1,0,C2,0,…,Cq,0，C表示类别，下标第1个数字表示类别数，下标第2个数字表示当前迭代次数；设定结束条件，令当前迭代次数e=0。根据计算类之间的距离，得到距离矩阵

图1 FMRDCHM流程Fig.1 Flowchart of FMRDCHM

图2 系统聚类流程Fig.2 Flowchart of hierarchical clustering

(19)

求距离矩阵中最小值(对角元素除外)，假设为Ci,0与Cj,0间的距离di,j，若di,j<1，则将Ci,0与Cj,0合并为新类Cij,1，建立新类C1,1,C2,1,…,Cq-1,1，即第1次迭代得到的1，2，…，q-1类。

b)根据计算合并后新类间的距离，得到新距离矩阵D1，设D1中最小元素为DA,B，且DA,B<1，则将类A、B合并为新类。

c)令e=e+1，跳转步骤b)，重复计算，当min|De|>1，停止迭代。

d)统计最终类数及每类包含的极点数，若极点数大于阈值n/4，则判定该类为物理模态，并以该类的平均值作为最终模态参数。

3 传递函数生成信号

为了通过类噪声信号评估本文方法的模态参数估计能力，首先在基于传递函数的模型上测试该方法，该模型产生的类噪声信号包含0.5 Hz和0.8 Hz 2种模态。模态的阻尼比分别为ξ1=2%和ξ2=5%，如图3所示。仿真模型使用均值为0、方差为1的高斯白噪声来模拟电力系统中负荷随机波动，用高斯白噪声作为模型的激励信号，并采用传递函数来模拟电力系统。再将2个传递函数的响应信号乘以图3中给出的系数，然后求和形成具有2种模态的类噪声输出信号。在该测试中，仿真时间为10 min，采样频率为100 Hz，生成的类噪声信号如图4所示，其中，s为传递函数的复参数，ω为模态频率对应的角速度，ξ为阻尼比。

图3 基于传递函数的包含2种模态的测试模型Fig.3 Test model based on transfer function with two modes

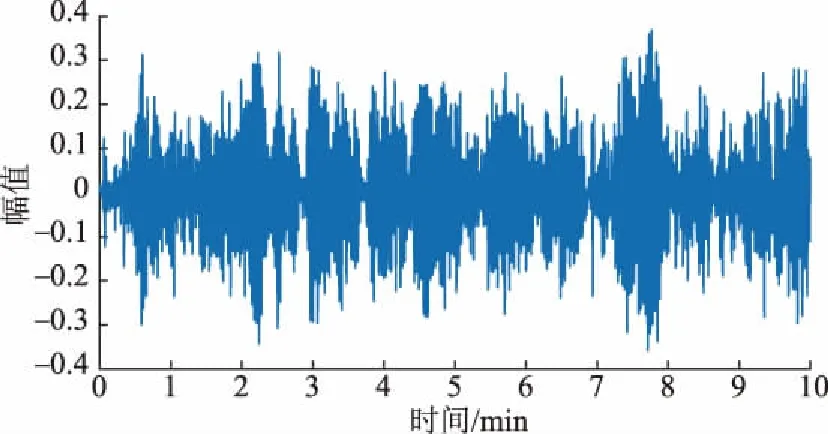
图4 基于传递函数生成的类噪声信号Fig.4 Ambient signals generated by transfer function

将2个汉克尔矩阵的行数设为100和80，模型阶数设为50。根据传统SSI得到的原始极点图如图5所示。从图5可知，虚假极点与物理极点交杂混叠，难以区分。

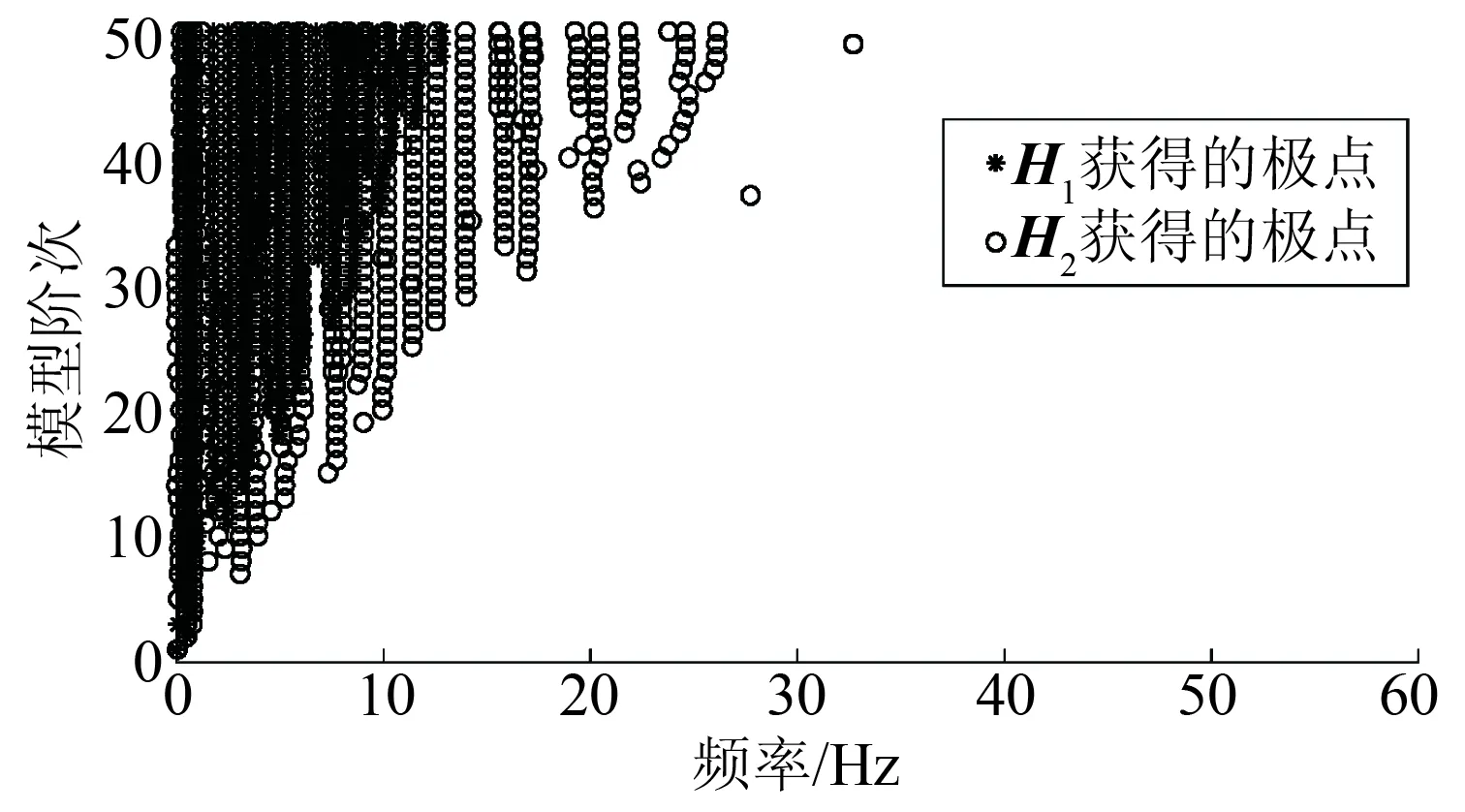
图5 原始极点分布Fig.5 Pole distribution

采用传统稳定图法进行虚假极点剔除，以频率为横坐标，模型阶次为纵坐标，建立稳定图，所得结果如图6所示。由图6可发现，相比于图5的模态识别结果中夹杂许多虚假极点，传统稳定图法所得图像已清晰许多，大部分虚假极点被剔除，但仍有部分虚假极点存在于最终结果中，被判定为物理极点，影响最终的模态识别结果。而基于本文方法得到的稳定图显然更加清晰，如图7所示，所有虚假极点均被剔除，所有物理极点均为真实模态对应的极点，剔除效果理想。

图6 传统方法稳定图Fig.6 Stabilization diagram obtained by traditional method

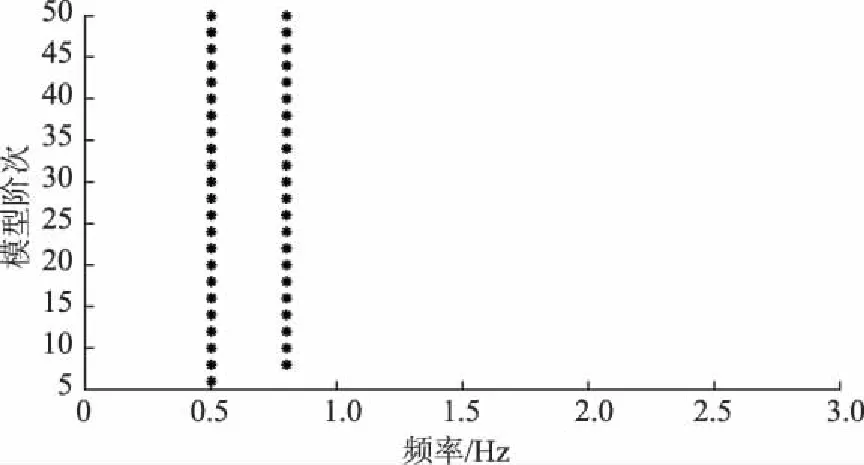
图7 本文方法稳定图Fig.7 Stabilization diagram obtained by the proposed method

采用传统稳定图法和本文方法进行模态辨识，结果见表1。

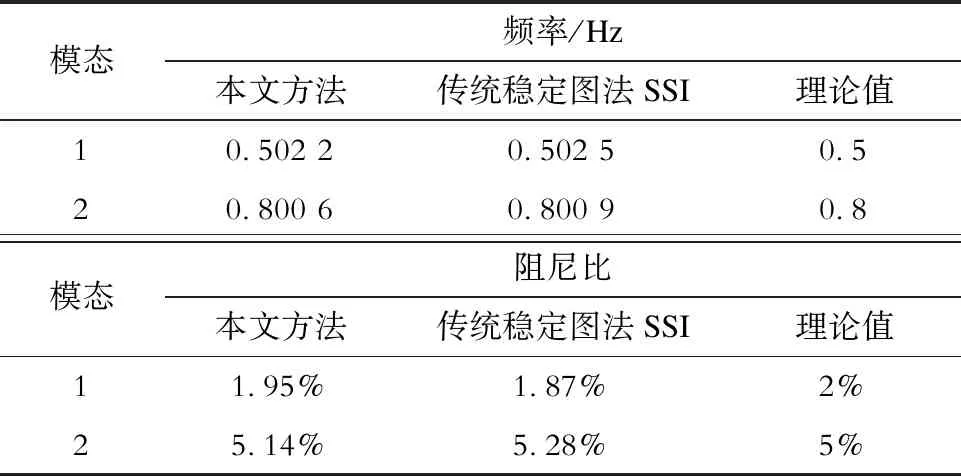
表1 传递函数生成类噪声信号的模态辨识结果Tab.1 Modal identification results of ambient signals generated by transfer function

基于传统稳定图法，模态1和2的估计值都较为精确，但若筛选经验不足则会出现虚假模态，虚假模态的出现会对后续制订低频振荡阻尼调制策略带来不利影响。通过本文方法计算得到的估计值均接近理论值：对于频率估计值，2种模态的频率估计误差均小于0.003 Hz，估计误差几乎可以忽略不计；而相比于频率，阻尼比的估计误差相对较大，但显然也符合精度要求。更重要的是，本文方法识别结果没有包含虚假模态，不会影响后续阻尼控制策略的制订。即便在模态混叠的情况下，本文方法也可以精确识别低频振荡模态参数。

4 IEEE WSCC 3机9节点模型及算法抗噪性能测试

前一个算例是基于理想的传递函数模型，在此算例中，采用由IEEE WSCC 3机9节点模型生成的类噪声信号来验证算法的性能，IEEE WSCC 3机9节点模型会更接近真实的电力系统。该系统在电力系统分析工具箱(power system analysis toolbox，PSAT)中构造，参数和结构设置根据文献[18]设置，模型如图8所示。在电力系统中，类噪声信号通常由负载中的实时随机波动引起，为了模拟电力系统中负载的随机波动，在该模型节点5、6、8处叠加30 dB的高斯白噪声[19]。

图8 IEEE WSCC 3机9节点系统Fig.8 IEEE WSCC three-machine nine-bus test system

同时基于PSAT自带的小稳定性分析功能进行线性化特征值分析(linear eigenvalue analysis，LEA)，为所计算的模态参数提供可靠的参考值。但是LEA是一种基于模型的方法，当模型较大时，计算成本高且不能满足实时性。根据LEA结果，系统有2种模态：频率f1=1.205 Hz、f2=1.831 Hz；阻尼比ξ1=2.514%、ξ2=6.125%。此外，根据PSAT产生的特征值报告，发电机3和发电机2各有一种模态，因此本文选择发电机3和发电机2间的相对角速度ω32作为分析信号，如图9所示。

图9 IEEE WSCC 3机9节点系统生成的ω32信号Fig.9 Ambient signalsω32generated by IEEE WSCC three-machine nine-bus system

模态辨识结果见表2。对于频率估计值，2种方法的真实模态1和2的结果均接近LEA结果，即频率误差很小；对于阻尼估计值，相比于传统稳定图法的SSI，本文方法更接近LEA结果，即误差更小。更重要的是，本文方法不会出现虚假模态3，因此本文方法的模态识别结果显然更有优势。虽传统稳定图法的平均计算时间(0.560 4 s)少于本文方法(0.616 9 s)，但牺牲较小的计算成本，获得更为精确的结果，显然是可以接受的。因此，本文方法更优于传统稳定图法SSI。

表2 不同方法下的模态辨识结果Tab.2 Modal identification resultsobtained by different methods

为了测试本文方法的抗噪能力，在测试信号上分别叠加信噪比为40 dB、35 dB、30 dB的高斯白噪声，模态辨识结果见表3。由表3可知，虽然噪声水平在不断增加，但频率的估计结果几乎与无噪声情况下的结果相同，阻尼比的估计结果相较于无噪声情况下结果的最大误差也仅为0.21%，说明本文方法具有良好的抗噪性。