摇摆条件下两环路自然循环回路特性分析

刘建昌，沈永刚，陈韵茵，杨 江，卢向晖

（中广核研究院有限公司，深圳 518026）

船舶、浮动平台等在运行过程中会伴随摇摆、起伏和倾斜等多自由度附加运动。在不同的海洋运动条件下，安装在船舶、浮动平台上的小型堆系统的流体会受到附加惯性力的作用，在附加惯性力的作用下，流体的流动、换热等会产生变化。

目前，世界上典型的大型压水堆核电站热工水力系统分析程序主要包括ATHLET、CATHARE、RELAP、TRACE等。上述程序适用于陆上核电厂，无法满足海洋条件下热工水力系统分析的需求。国内外针对RELAP5与RE⁃TRAN开展了海洋条件下的适用性研究。

Toshihisa ISHIDA[1]在RETRAN-02的基础上增加了倾斜、垂直加速、起伏以及任意角度旋转的模型，通过二次开发得到了用于海洋条件下船舶核动力装置热工水力瞬态分析程序RE⁃TRAN-02/GRAV。Jae-Hak Kim等根据RE⁃TRAN-03程序引入相关海洋条件模型形成了RETRAN-03/MOV[2]与RETRAN-03/INT[3]。

谭长禄等在RELAP5的基础上，在考虑海洋条件下引入的附加力模型，通过二次开发得到了海洋条件下热工水力分析程序RELAP5/MC[4]。

于雷、鄢炳火分别基于RELAP5/MOD3.2与RELAP5/MOD3.3开发了海洋条件下的系统分析程序[5-7]。二者均通过修改汽液混合物的动量方程描述海洋条件引起的附加压降，同时，在程序中考虑了摇摆对摩擦系数、换热系数的影响。

本文基于海上小型堆安全分析的需求，建立了海洋运动条件下的附加惯性力模型，并对RELAP/SCDAP程序进行修正。然后，简单介绍海洋运动条件下的附加惯性力模型，并利用修正后的RELAP程序建立自然循环回路模型，在摇摆条件下分析自然循环回路的热工水力特性。

1 适用于海洋运动条件的热工水力系统分析程序

在对RELAP/SCDAP程序二次开发前，首先需要建立相应的附加惯性力模型，根据建立的模型修正RELAP程序中的动量方程，最终得到适用于海洋运动条件的热工水力系统分析程序。本节重点介绍附加惯性力模型。

建立附加惯性力模型时，通常会分别建立起伏、摇摆和倾斜等单一海洋条件下的附加惯性力以及不同海洋条件耦合的附加惯性力模型。本文在建立附加惯性力模型时，从附加惯性力的通用格式出发，根据平动、转动和倾斜的数学模型，推导得到通用的附加惯性力模型，可以用于分析不同的单一海洋条件以及不同海洋条件耦合的情况。

1.1 惯性坐标系和非惯性坐标系

分析海洋运动条件下的附加惯性力时，首先需要建立一套惯性坐标系和一套非惯性坐标系。

本文假设在静止条件下，惯性坐标系O0X0Y0Z0原点与海上小型堆的重心重合，X轴与海上小型堆的轴线重合。非惯性坐标系OXYZ为控制体坐标系，原点固定在控制体的几何中心上，且坐标轴分别与惯性坐标系O0X0Y0Z0的3个坐标轴平行。随着海上小型堆的运动，非惯性坐标系也随着运动，如图1所示。在分析过程中，本文对每个控制体在相应的非惯性坐标系OXYZ中建立动量方程。

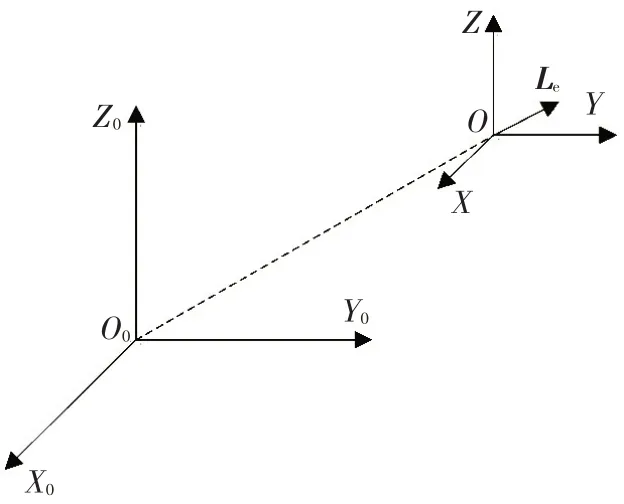
图1惯性坐标系和非惯性坐标系Fig.1 Inertial&non-inertail coordinates

1.2 海洋运动条件的数学模型

海洋运动条件可以分为倾斜、起伏、摇摆。在海浪、风、船的机动条件下，小型堆可能会发生不同的运动方式，包括平动、转动和倾斜。本节将简单介绍各种运动条件的数学模型。

1.2.1 平动数学模型

平动包括沿X轴方向的加速、沿Y轴方向的平移、沿Z轴方向的起伏或加速运动，可用下列矩阵表示：

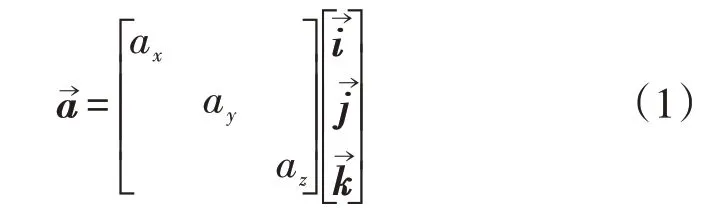
式中，ax、ay和az——沿X、Y、Z轴的加速度；

1.2.2 转动数学模型

转动包括绕X轴的横摇、绕Y轴的纵摇、绕Z轴的转动，转动数学模型可以用下列矩阵表示：

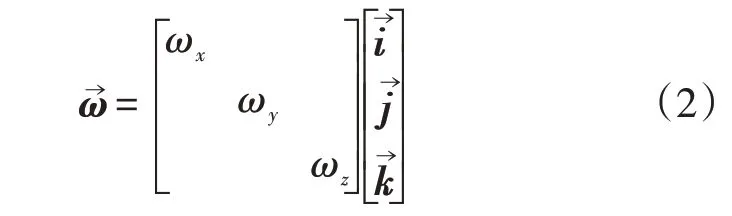
式中，ωx、ωy和ωz——横摇、纵摇和绕Z轴的转动角速度。

1.2.3 倾斜数学模型

在海洋运动条件下，海上小型堆与X、Y和Z轴之间的夹角分别为θx、θy和θz。倾斜运动会影响各个设备之间的相对位置，造成自然循环驱动力的改变。

1.3 附加惯性力模型

根据控制体内流体流速u→r和控制体在惯性坐标性中的位置r→，可以得到海洋运动条件下，控制体所受到的附加惯性力的通用格式为[8]：

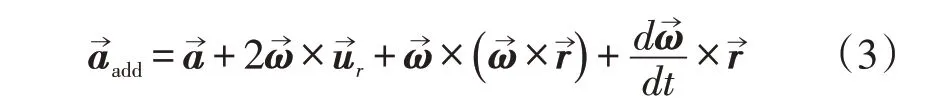
考虑到RELAP/SCDAP程序为一维程序[9]，而科氏力2ω→×u→r始终与流体流动方向垂直，不会直接影响流动过程，因此，本文在修正RE⁃LAP/SCDAP程序时忽略该项的影响。根据附加惯性力的特点，可以将附加惯性力分解为平动引入的附加力和转动附加惯性力a→2两部分：

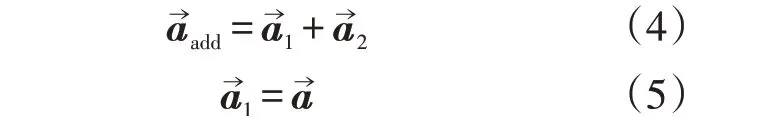
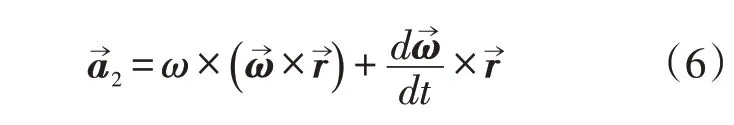
式（4）中的附加力是三维矢量，对RE⁃LAP/SCDAP进行修正以前，需要得到流体所受到的附加惯性力沿流动方向的分量。

某一控制体内流体在非惯性坐标系OXYZ的流动方向的附加力可用单位向量坐标■→Le表示：

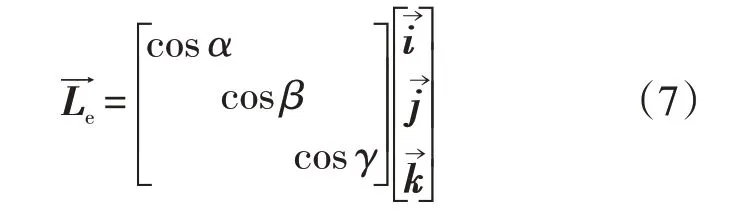
在海洋条件下，控制体绕任意轴旋转后的流动方向附加力为：

式中，R——绕任意轴旋转的旋转矩阵[10]，R=Rz(θz)Ry(θy)Rx(θx)。

根据式（5）和式（8），平动附加惯性力沿流动方向上的分量为

在倾斜或摇摆条件下，控制体所在位置、倾角发生改变，流体所受到的重力沿流动方向的分量如式（10）所示。

1.4 RELAP/SCDAP程序修正

本文根据所建立的附加惯性力模型（式（10）～式（12）），对RELAP/SCDAP程序修正。在进行海洋条件下热工水力分析程序开发时，本文仅考虑了海洋条件引入的附加惯性力影响，对程序中动量方程进行了修正，在程序中未进一步对海洋条件下的阻力模型、传热模型等进行修正。

2 摇摆条件下自然循环回路特性

本节中将利用修正后的RELAP程序，建立两环路自然循环回路的模型，并开展摇摆条件下的自然循环特性分析，自然循环回路模型如图2所示。

在分析中，假设坐标系原点为热源下封头的几何中心，竖直方向为Z轴，自然循环回路所在平面为Y轴，如图2所示。分析时，假设横摇运动模型为简谐运动，t时刻，横摇角度模型如式（13）所示。

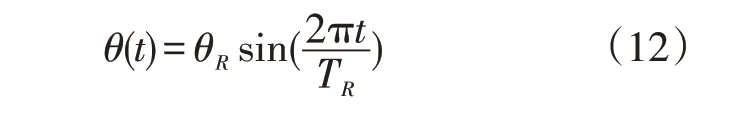
式中，θR——横摇角幅值；

TR——横摇周期。

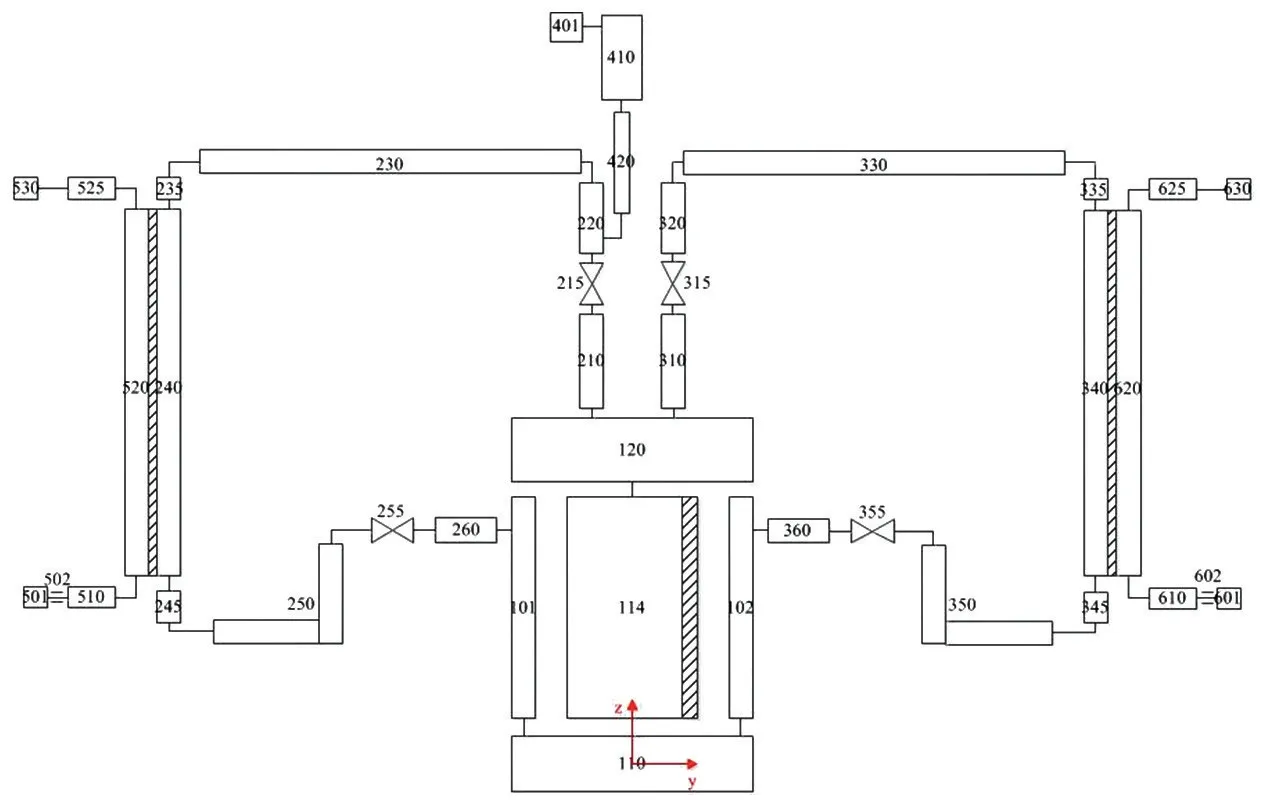
图2自然循环回路模型Fig.2 Modelsof the natural circulation loop

2.1 摇摆条件下的自然循环回路特性

本节首先分析摇摆幅值为5°、周期为30 s下的自然循环回路特性，横摇运动模型如图3所示，计算结果如图4～图6所示。

在摇摆工况下，左、右环路冷源与热源之间的高度差发生周期性变化，且左、右环路的变化刚好反相，因此，环路流量发生周期性波动，流量波动周期为横摇运动周期，左、右环路之间流量波动的相位差为π。热源的流量取决于左、右环路的流量，在横摇工况下，热源的流量波动幅值较小。

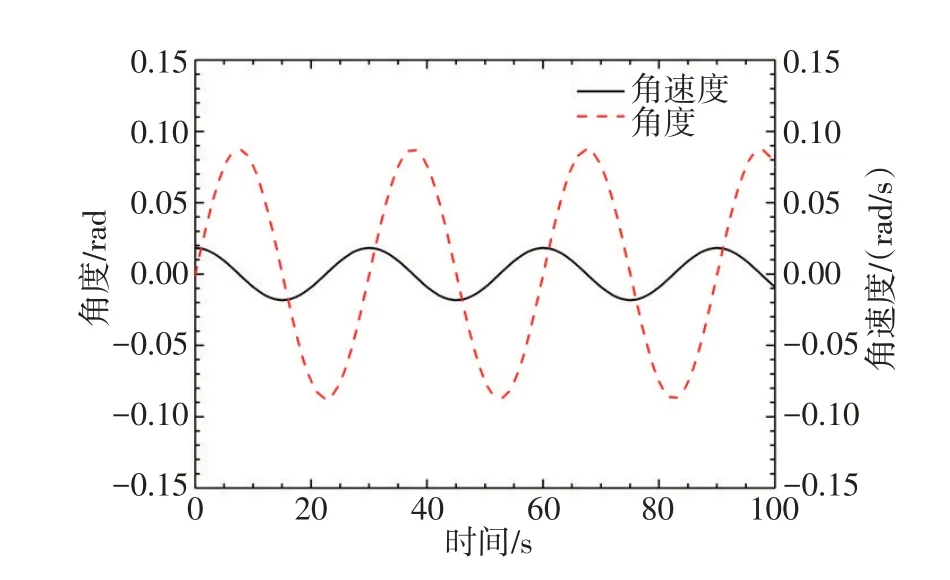
图3横摇运动模型（幅度=5°，周期=30 s）Fig.3 Rolling model（amplitude=5°,period=30 s）

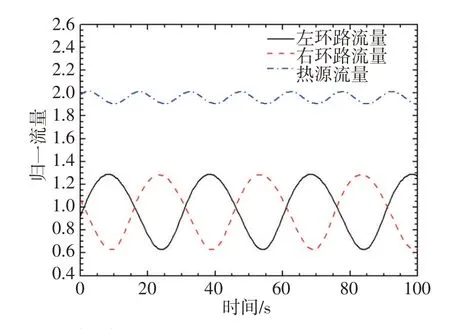
图4横摇条件下归一流量1.横摇条件下流量与静止条件下环路流量之比。（幅度=5°，周期=30 s）Fig.4 Normalized flow under swing conditions（amplitude=5°,period=30 s）

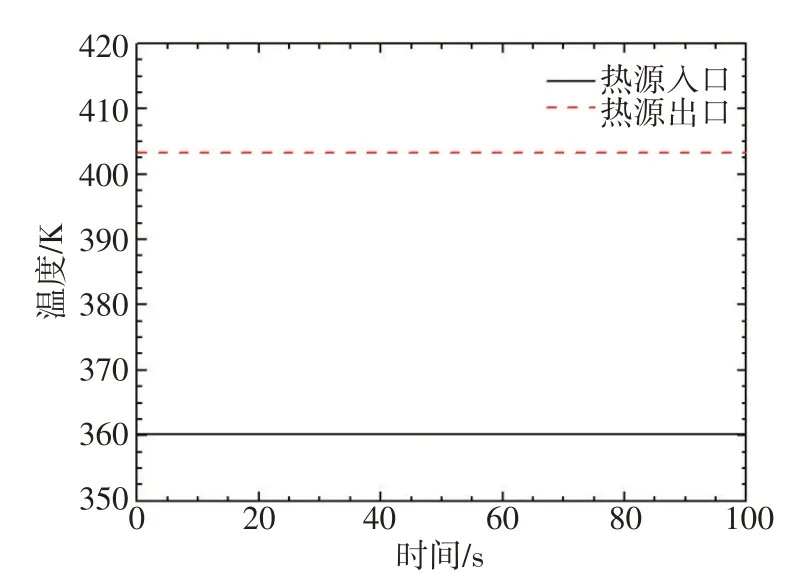
图5自然循环回路温度（幅度=5°，周期=30 s）Fig.5 Temperatureof thenatural circulation loop（amplitude=5°,period=30 s）

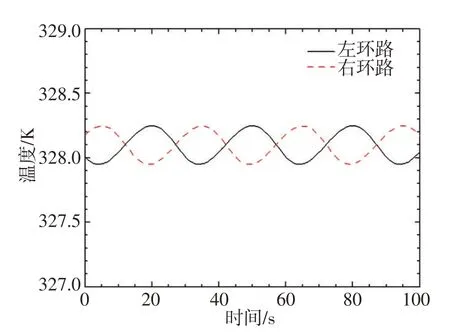
图6冷却水出口温度（幅度=5°，周期=30 s）Fig.6 Cooling water temperature of the outlet（Amplitude=5°,Period=30 s）

对左环路而言，当角加速度为正时，摇摆产生的附加力沿流动方向的分量与流动方向相同，此时，横摇产生的附加力起驱动力的作用，因此，左环路的流量逐渐增加。当角加速度为负时，附加力沿流动方向的分量与流动方向相反，此时，横摇差生的附加力起阻力的作用，左环路的流量逐渐减小。由于流动惯性的作用，自然循环流量波动滞后于横摇运动。

左、右环路流量周期性波动，引起冷源一次侧出口的温度发生周期性变化，两个环路的温度变化的相位差为π。左、右环路的水在热源下降段和下封头均匀混合后进入加热区域，由于左、右环路的流量、温度波动曲线存在相位差，叠加后导致在加热区域入口的流量、温度的波动幅值较小。在恒定的加热功率下，热源出口的温度基本不变。

由于左、右环路的流量波动幅值较大，冷源的换热功率也发生周期性变化，冷源入口流量和温度为恒定值，因此，冷源出口的冷却水温发生周期性变化，当环路的自然循环流量增加时，冷源的换热功率增加，冷源出口的冷却水温增加；流量减小时，换热功率减小，冷却水温下降。由于存在热惯性，冷却水温的波动滞后于流量波动。

2.2 摇摆幅度对自然循环特性的影响

本节中分析摇摆角度幅值对自然循环流动特性的影响。摇摆周期为30 s的不同摇摆角度幅值的计算结果如图7所示。

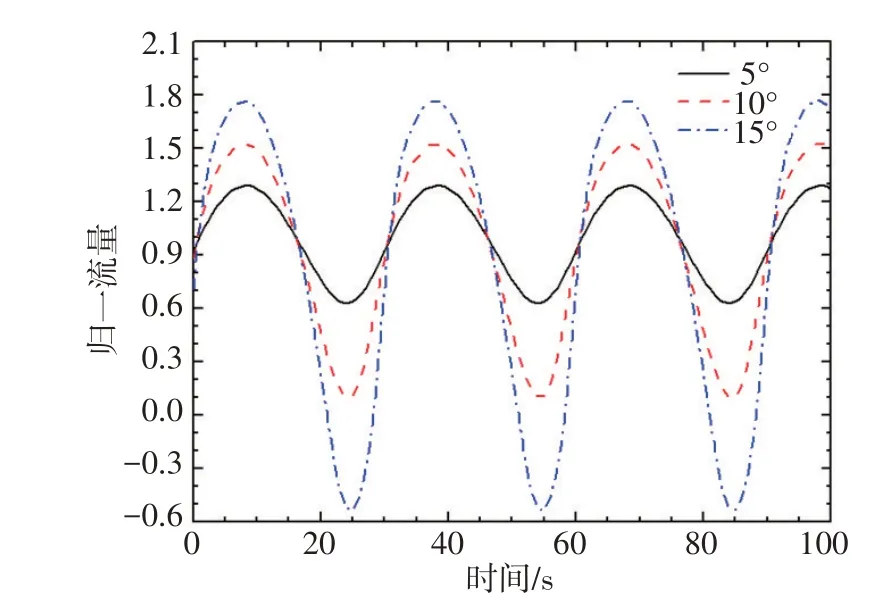
图7摇摆幅值对自然循环流量的影响（周期=30 s）Fig.7 Effectsof therolling amplitudeson natural flow rate（period=30 s）

在相同的摇摆周期内，摇摆幅值越大，摇摆的角速度和角加速度越大，流体所受到的附加作用力越大。同时，摇摆幅值越大，冷、热源之间的高度差越大，自然循环驱动力变化越明显。在两种变化的作用下，摇摆幅值越大，流量波动越剧烈。

在摇摆条件下，自然循环流量的平均值小于静止条件的流量，摇摆幅值越大，自然循环流量的平均值越小。

从计算结果可以看出，当摇摆幅值为15°时，左、右环路的流量出现了负值，与左、右环路的驱动压头有关。在摇摆角较大时，一侧环路的驱动力较大，而另一侧的驱动力较小，在这种情况下，驱动力较小的环路流量出现了负值。

2.3 摇摆周期对自然循环特性的影响

摇摆幅值为10°时，不同摇摆周期条件下的计算结果如图8所示。摇摆周期越短，摇摆角速度和角加速度越大，附加力越大，流量波动越剧烈。摇摆周期越短，自然循环流量的平均值越小。

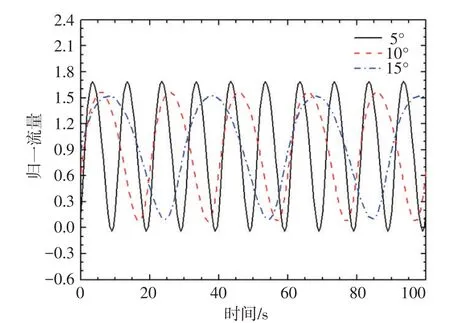
图8摇摆周期对自然循环流量的影响（幅度=10°）Fig.8 Effects of therolling periodson natural flow rate（amplitude=10°）

3 减小横摇对自然循环影响的方法

横摇条件下，自然循环主要受自然循环驱动力、系统阻力以及周期性变化的附加惯性力的影响。当横摇运动较剧烈时，自然循环流量会出现较大幅度的波动，甚至在环路上会出现倒流。

为减小横摇运动对自然循环的影响，可以考虑提高自然循环驱动力，如提高系统加热功率、增加冷热源之间的高度差等方式。

3.1 提高系统功率

在一定的横摇条件下，提高系统的加热功率，提高自然循环驱动力，就能减小横摇的影响。横摇幅度为15°、周期为30 s情况下的计算结果如图9所示。

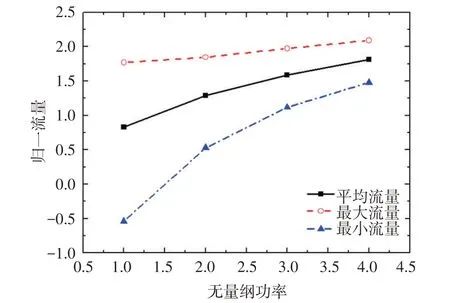
图9提高加热功率的计算结果（幅度=15°，周期=30 s）Fig.9 Resultsof increasing heating power（amplitude=15°,period=30 s）

在摇摆条件下，平均流量随加热功率的增加而增加，而流量的波动幅值随加热功率的增加而逐渐减小。功率逐渐增加后，环路上的倒流现象逐渐消失。

3.2 增加冷热源之间的高度差

在加热功率不变的情况下，改变冷源位置可以改变冷热源之间的高度差，计算结果如图10所示。

当冷热源之间的高度差增加时，自然循环驱动力增加，流量逐渐增加，流量的波动幅值也逐渐减小。由于加热功率较低，冷热源之间的密度差较小，增加冷热源之间的高度差对自然循环驱动力的影响相对较小。

在横摇条件下，提高加热功率或增加冷热源之间高度差，能提高自然循环流量，减小流量的波动幅度。当受空间布置影响，冷热源之间的高度差固定时，适当的提高加热功率能有效的减小横摇对自然循环的影响。

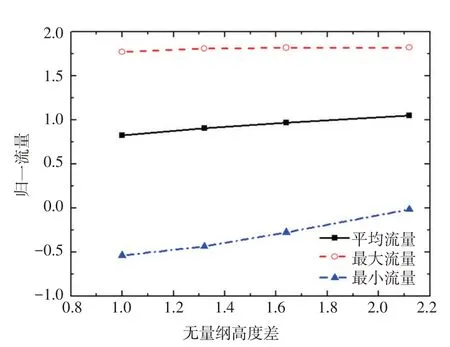
图10增加冷热源之间高度差的计算结果（幅度=15°，周期=30 s）Fig.10 Resultsof increasing height differencebetween heating and cooling source（Amplitude=15°,Period=30 s）

4 结论

本文根据RELAP/SCDAP程序的特点，建立了相应的附加惯性力模型，得到了适用于海洋运动条件的系统分析程序，分析了摇摆条件下自然循环回路的热工水力特性，得到以下结论：

（1）在摇摆工况下，左、右环路的流量发生周期性波动，流量波动周期为横摇运动周期，且左、右环路之间流量波动的相位差为π。而热源的流量波动幅值较小，波动周期为横摇运动周期的1/2。

（2）摇摆幅值越大，周期越短，自然循环流量波动越剧烈。

（3）摇摆较剧烈时，环路上会出现周期性的倒流。

（4）增加加热功率或提高冷热源之间高度差可以增加系统的自然循环驱动力，能减小横摇对自然循环的影响。