使用动量交换装置的滚转角稳定控制∗

杨 帆

（中国船舶重工集团有限公司第七一〇研究所 宜昌 443003）

1 引言

为满足诱饵火箭弹作战需求，缩短调节时间，提高滚转通道稳定性和抗扰动能力，提出滚转通道与俯仰偏航通道解耦的控制方式。借鉴卫星姿态控制方式，采用动量交换装置实现滚转角稳定控制。动量轮具有可靠性高、控制精度高和功耗低等优点，已被广泛应用于卫星姿态控制中［1～2］。

滚转通道执行机构为直流力矩电机，具有非线性性、参数不确定性和易受外部扰动因素的影响等特点［3］。滑模控制由于滑动模态可以进行设计，且与控制对象参数和扰动无关，无须在线辨识等优点［4］，所以在解决这些问题方面表现优秀。

本文从现有实际需求出发，建立了滚转通道动力学模型和动量轮动力学模型，设计了滚转通道控制系统，其中，外回路采用PID控制算法，动量轮内回路采用滑模控制算法提高系统抗扰动能力，并开展了仿真研究，为诱饵火箭弹的设计提供了一种可能性。

2 控制模型建立及分析

动量交换控制的基本原理就是动量矩定理，系统的总动量矩矢量对时间的导数，等于作用在系统上外力矩矢量之和。如果利用某些控制执行机构将系统的一部分的动量矩发生改变，则系统其余部分的动量矩将发生大小相等方向相反的改变。

2.1 控制原理

在诱饵弹三通道控制模型中，滚转通道与俯仰偏航通道设计解耦，在进行滚转运动研究中，我们假定ωx=ωz=0；ϑ=ψ=0。诱饵火箭弹滚转通道动力学模型为

根据动量矩定理可以得到滚转力矩表达式为

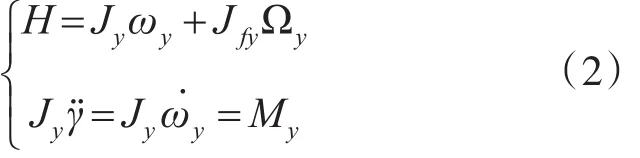
其中，H为系统总动量矩，Jy为诱饵火箭弹（含转子舱）绕 y轴的转动惯量，Jfy为转子舱绕 y轴的转动惯量，ωy为诱饵火箭弹绕y轴的转动角速度，Ωy为转子舱相对火箭弹绕 y轴的转动角速度，γ为火箭弹滚转角。

2.2 动量轮动力学模型

滚转角的高精度控制实质上就是动量轮的高精度转速控制。动量轮工作原理如下：当动量轮内的电机绕组中按规律通入电流时，电机产生转矩（最终达到一定的转速）从而形成一定的动量，该转矩或动量作用到动量轮的安装载体上，就会改变载体滚转角或抵抗扰动转矩［5～7］。假设［8］：

1）电机的气隙磁感应强度沿气隙按正弦分布。

2）绕组通电时，该电流所产生的磁通对气隙磁通的影响忽略不计。

3）控制电路在开关状态下工作，功率器件压降为恒值。

4）各项绕组对称，其相应的电路单元完全一致，相应的电气时间常数忽略不计。

根据永磁电机原理［9～10］有：

动量轮动力学模型如图1所示。

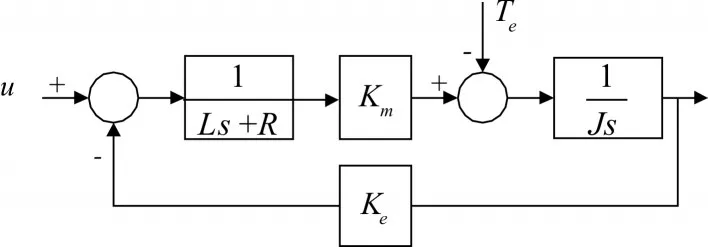
图1 动量轮动力学模型

由控制器给出控制电压，使动量轮转速变化，改变转子舱的动量矩，并输出反作用力矩作用于诱饵火箭弹。动量轮理想传递函数为

2.3 动量轮动力学模型修正

在实际工作中，动量轮并不理想。一方面，电机内部存在摩擦阻尼。且摩擦力矩为非线性，会随着工作环境发生变化；另一方面，存在扰动力矩的作用。本文在模型处理时，将摩擦力矩和扰动力矩作为外部扰动融合到电压扰动中。由此得到电机转速与输入电压的关系为

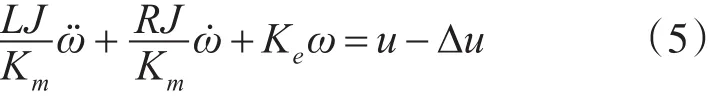
3 控制算法设计

诱饵火箭弹滚转角回路采用PID控制算法，动量轮电机采用滑模控制算法。

3.1 PID控制算法

PID控制算法的数学模型［11］为

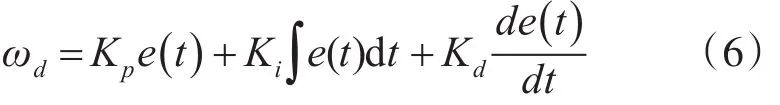
其中，ωd为动量轮电机的期望转速；e(t)=γ(t)-γd(t)为滚转角误差；Kp、Ki和Kd是控制器的比例、积分和微分增益。

控制系统结构图如图2所示。

图2 控制系统结构图

3.2 滑模控制算法

针对式（5）的控制问题，采用滑模控制［12-13］思想分别设计等效控制器和切换控制器。

1）滑模面设计

滑模面 s=ce+e˙，其中 c≥0，e=ω-ωd为电机转速误差。

2）等效控制器（不考虑扰动）

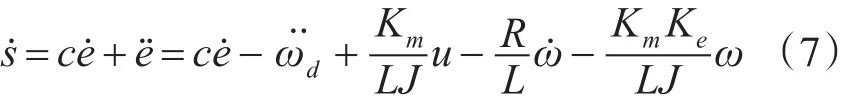
取s˙=0可知不存在扰动时的等效控制律u1为

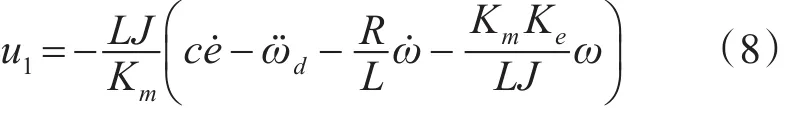
3）切换控制器

切换控制器用来克服外部扰动，设克服扰动的切换控制律为u2，那么动量轮的实际控制律u=u1+u2。

其中，g为外部扰动，外部扰动大小未知，但有界。设‖‖g≤G。

在动量轮高精度控制中，输入电压幅值有限，设幅值上限为umax。

引入饱和函数sat(u)，则实际输入电压为

4 仿真分析

数值仿真建立在Matlab的Simulink环境中，诱饵火箭弹及动量轮电机参数如表1所示。

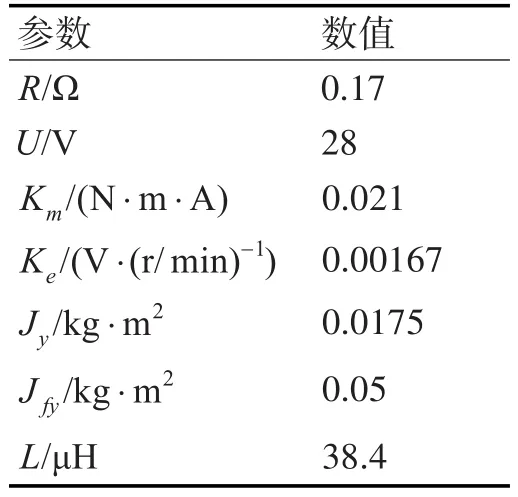
表1 诱饵火箭弹及动量轮参数

设定期望滚转角 γd=0°，滚转角初始值γ=20°，取 kp=20.16，ki=0.01，kd=0.58，c=2，k=-2.25，采用本文设计的控制器和控制算法。仿真曲线图如图3所示。图3为无扰动时的控制效果图。

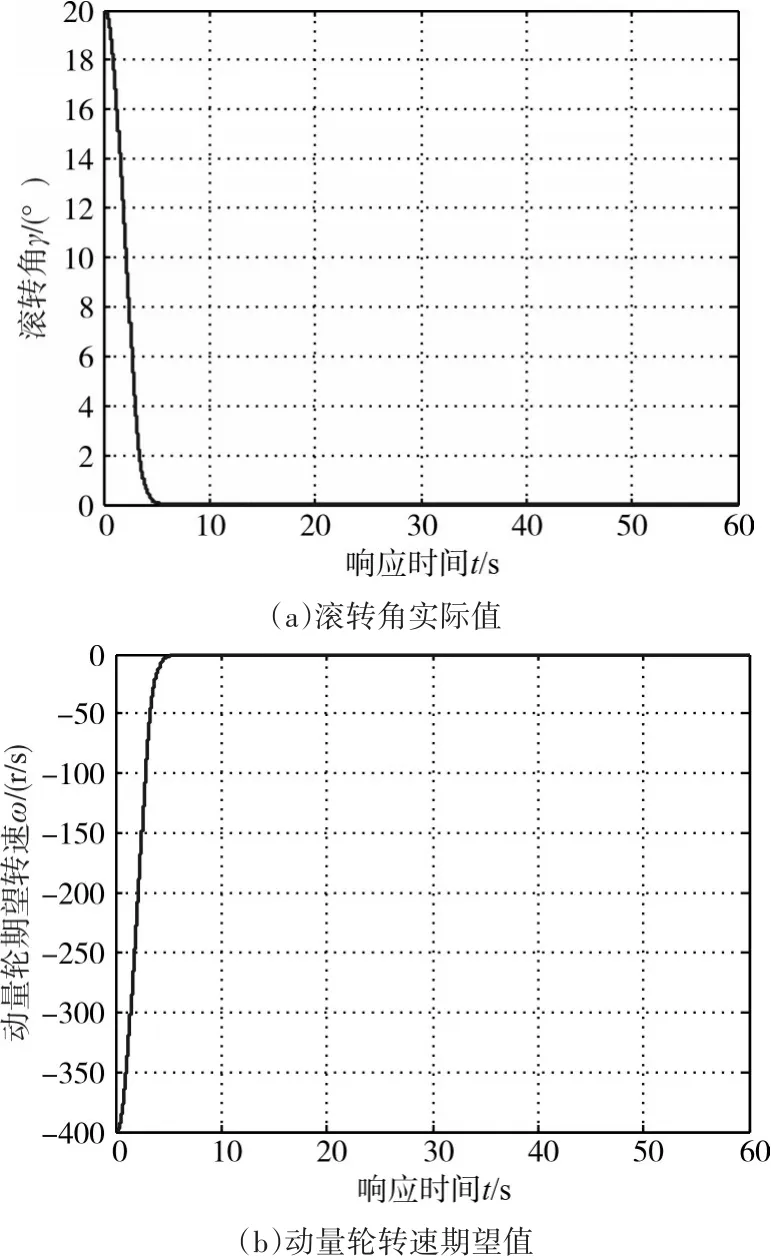
图3 无扰动时的控制效果图

诱饵火箭弹在工作过程中，会受到各种扰动因素的影响，既有外部扰动，也有内部扰动。本文将外部扰动等效于实际滚转角的一部分反馈回仿真模型中，将内部扰动等效于电机输入电压误差∆u，也就是滑模控制器需要解决的外部扰动量作用于电机回路。

设定期望滚转角 γd=10°，滚转角初始值γ=0°，在30s时分别加入等效幅值为1°，周期为30s脉冲占比为10%的外部脉冲扰动和等效幅值为5°，周期为30s脉冲占比为10%的内部脉冲扰动，仿真结果如图4和图5所示。图4为外部扰动时的控制效果图，图5为内部扰动时的控制效果图。

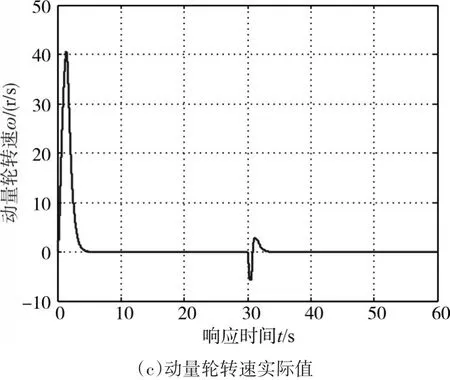
图4 外部扰动时的控制效果图

图5 内部扰动时的控制效果图

设定期望滚转角 γd=10°，滚转角初始值γ=0°，同时加入内部和外部两种扰动，其中，在30s时加入等效幅值为5°，周期为30s脉冲占比为10%的内部脉冲扰动，在37s时加入等效幅值为1°，周期为30s脉冲占比为10%的外部脉冲扰动，仿真结果如图6所示。图6为外部和内部扰动同时作用下的控制效果图。

图6 两种扰动时的控制效果图

仿真结果表明：诱饵火箭弹在PID控制和滑模控制作用下能快速到达期望滚转角附近，调节时间在4s以内，响应速度快，稳态误差几乎为零，控制精度满足要求。从图5～图7可以知道，控制系统具有很强的控制能力，对内部和外界扰动具有很强的鲁棒性，使用动量交换装置的滚转通道具有稳定性，控制方案可行。

5 结语

本文主要对诱饵火箭弹滚转通道进行了研究，建立了滚转通道的动力学模型，针对其执行机构与常规火箭弹的差异，进行了建模和控制算法研究，设计了控制系统。对系统外回路设计PID控制器，对动量轮电机设计滑模控制器，并通过仿真验证了控制系统的有效性，对诱饵火箭弹滚转通道的后续研究具有一定参考价值。