洪峰流量推求方法实例分析

孙全章

摘  要：在实际洪峰实测过程中，常常会因为各种问题，而无法实测到洪峰的最大流量，如何能合理有效的推求出洪峰流量，就成为了一个难以解决的问题。文章以西南岔河南岔站为例，通过南岔站的实测资料，利用水力学原理推求南岔站的最大洪峰流量，并进行对比分析，提出可供参考性意见。

关键词：西南岔河流域;最大洪峰流量;水力学;水位流量关系

中图分类号：P338         文献标志码：A         文章编号：2095-2945（2020）05-0133-02

Abstract： In the actual flood peak measurement process， often because of a variety of problems， the maximum flow of the flood peak can not be measured， how to reasonably and effectively deduce the flood peak flow has become a difficult problem to solve. In this paper， taking the southwest bifurcation Henan bifurcation station as an example， based on the measured data of the south bifurcation station， the maximum flood peak discharge of the south bifurcation station is deduced by using the hydraulic principle， and the comparative analysis is carried out， and some suggestions are put forward for reference.

Keywords： southwest Chahe River Basin; maximum flood peak discharge; hydraulics; water level-discharge relationship

1 概述

在大洪水過程中，常常会因为各种因素，无法实测到洪峰流量，因此在某些情况下，需要进行洪峰流量等资料的推求。通常在有糙率和比降资料的地区，可直接通过水力学谢才-曼宁公式推求，但在无糙率、比降资料等地区的洪峰推求较为困难。本文通过对实测资料的分析及结合谢才-曼宁公式，通过两种方法来推求洪峰流量，并进行对比分析。

2 洪峰推求两种方法

2.1 谢才-曼宁公式

谢才-曼宁公式是总结河渠均匀流情况，得出的计算过水断面平均流速v的公式：

式中R为水力半径;J为比降;n为糙率。如果可知断面面积A，则就可知断面流量Q：

2.2 无糙率和比降资料的推求方法

对无糙率和比降的测站，可通过水位流量关系线与谢才-曼宁公式相结合作高水延长，从而推求洪峰流量。根据水位与流量存在的相关关系，可知水位与式（2）也同样存在着相关关系，将式（2）中■J■与AR■分别设为a和b，则（2）式就可改写为：

水位Z分别与a、b两项存在相关关系，那么水位与这两项也分别可绘制关系曲线，通过相关的曲线延长计算就可求得洪峰流量。

3 实例流域计算分析

3.1 流域概况介绍

西南岔河为汤旺河下游右岸支流，流域面积2757km2，属典型的山溪性河流，流域洪水为暴雨径流型洪水。南岔水文站是西南岔河的出口控制站。

3.2 洪水概况

2018年受台风影响，西南岔河流域发生特大洪水。南岔站于2018年7月26日出现洪峰，由于安全等因素考虑，无法实测洪峰水位与流量，后经洪水调查知洪峰水位为95.08m，洪峰流量约950m3/s。

3.3 无糙率比降的洪峰流量推求

无糙率比降的洪峰流量推求其主要是依靠水位流量关系线，与谢才-曼宁公式两者有效结合做高水延长，来推求最高洪峰流量，现可知南岔站部分实测资料见下表1。

由表1可知西南岔河南岔站为宽浅河道，则水利半径R可用平均水深代替，由此可计算a与b两个相关项。通过已知断面面积及平均水深，即可计算a值，由a值则可计算b值，计算成果见下表2。

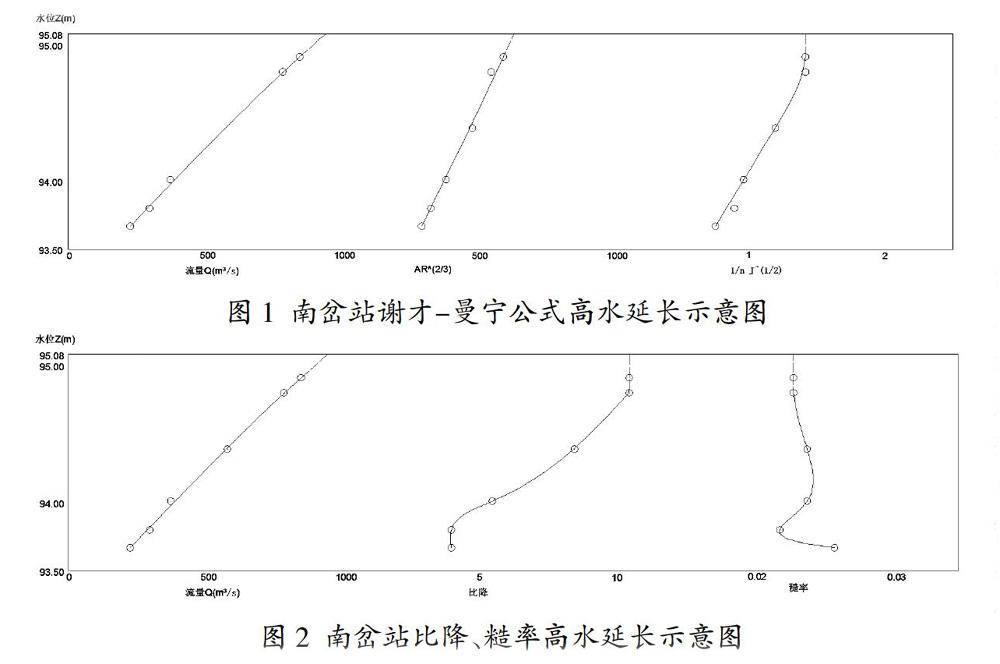
根据表2绘制水位与流量、a、b三项相关图。在高水部分，断面的糙率n与比降J都接近常值，因此J值也趋于常值不变，则在高水延长时就可顺势进行顺直延长，并顺势延长AR线，详情见图1。

从图1中可查得J值为1.42，AR值为639，从而求得相应洪峰流量约为907m3/s。

3.4 根据糙率比降的洪峰流量推求

由表1可知部分实测流量的糙率比降，利用表1绘制水位与流量、比降、糙率三项相关图。在高水部分的比降与糙率均接近一个不变的常值，由此进行高水趋势延长，详情见图2。

从图2中可查得比降J为10.5，糙率n为0.023，根据大断面计算面积A为377m2，平均水深为2.5m，根据式（3）求得相应洪峰流量约为978m3/s。

4 对比分析

由表3可知，无糙率比降推求的洪峰流量与洪水调查的洪峰流量相差约4.5%;利用糙率比降法推求的洪峰流量与洪水调查的洪峰流量相差约2.9%。由此可见利用比降糙率推求的洪峰流量结果更加的接近真实的洪峰流量，此种方法比无糙率比降法的结果更加准确。但比降糙率法所需要的数据资料较多计算较为麻烦，无糙率比降法相较糙率比降法更加简单方便快捷，化零为整的参数整合，也避免了很多参数的计算误差，这种方法的计算结果误差也在洪峰流量推求的允许误差之内，并且无糙率比降法对于大多没有糙率比降资料的中小河流更加适合。

5 结束语

无糙率比降法的洪峰流量推求，比较适合一些天然河道，对主槽稳定，河道呈宽浅式的河流运用有较好的效果，对窄深式河道并不适用。若在高水位发生漫滩的时候，主槽和漫滩部分应分别计算流量进行延长。对于一些资料较少的情况下，这是一种可以计算洪峰流量较为便捷的方法。文章所举实例数据较少，仅提供方法参考。

参考文献：

[1]包为民.水文预报[M].水利水电出版社，2009.

[2]芮孝芳.水文学原理[M].中国水利水电出版社，2004.