深海VLFS结构双参数尺寸优选分析

杨琳 刘文白

摘要：为获得结构强度高、抗浪性强、稳定性好的深海超大型浮式结构（VLFS）型式，本研究采用同时改变两个参数的双参数优选方法进行结构尺寸的优选，将三层网架高度2H和腹杆与水平面夹角α作为一组变量参数，球节点和杆件直径D1、D2作为第二组变量参数，球节点和杆件壁厚T1、T2作为第三组变量参数进行结构的参数优选，运用大型有限元软件ABAQUS对三组共11个参数模型进行了计算分析，综合考虑各尺寸参数对结构在静力、动力荷载作用下的结构应力、极限承载力以及结构的耗钢量的影响，进而进行尺寸比选，最终得到了较优的网架结构型式，并总结得出不同参数对浮式网架结构力学性能的影响。

关键词：超大型浮式结构;数值模拟;ABAQUS;尺寸优选;应力;极限承载力

0 引言

随着时代的发展，人类社会在进步的同时，也面临着诸如陆地空间紧张，资源匮乏严重的严峻形势，将发展重心转向海洋已成为全世界各重大领域刻不容缓之要务[1]。面对发展海洋特别是深海领域的重大任务，超大型浮式结构（VLFS）的研究应运而生。超大型浮式结构是应用于深海的新型海洋结构，将对其所在区域的社会、经济、军事方面产生重要影响，其结构设计成为关键课题之一。处于深海环境的VLFS结构环境因素复杂，作为深海工程的基础，将承受巨大的工程荷载，故超大型浮式结构的稳定性、安全性、耐久性和经济性需达到各方面最优。

本研究对影响超大型浮式结构的几个关键性参数进行尺寸优选，意在得到强度高、消浪性能好、满足实际工程需要的较优结构型式。研究工具选用大型有限元分析软件ABAQUS，其在求解大型线性或非线性问题上具有很强的优越性[2]，适用于本研究中的大尺度海洋浮式网架结构的静、动力分析计算。

1 有限元建模

数值模拟技术通过计算机有限元软件（如ABAQUS、ANSYS等），利用迭代算法能快速求解复杂矩阵，从而解决物理研究及实际工程中的问题。数值模拟技术结合了有限元的概念，不仅有效提高了有限元运算的效率，其计算结果的可视化也使得研究结论更为生动直观。相较于物理实验，数值模拟技术在有效节约时间及成本的同时，试验结果也能得到保障，特别适用于海洋VLFS结构的力学特性研究。通过对大量海洋结构有限元模拟研究[3-7]进行参考，决定采用大型有限元分析软件ABAQUS进行VLFS结构的模型分析。

1.1 分析模型

通过比选分析，超大型浮式网架整体选用正放四角锥三层网架结构型式，其在力学性能、跨度适用范围以及工程可实施性上较其他型式更优。分析对象选取超大型浮式网架结构中心位置的一榀桁架（如图1所示），主要由球节点、腹杆、水平杆这三个基本部件组成。球节点外径为6.5m，壁厚为25mm;腹杆长为10.437m，外径为2.13m，壁厚为25mm;水平杆长为5.459m，外径为2.13m，壁厚为25mm。以三个基本部件为基础，根据桁架结构的对称性，通过线性阵列、辐射性阵列、旋转等方法得到分析对象的整体结构型式，有效降低了工作难度。[KH-*1/1]

此海洋网架为钢结构，根据《船舶及海洋工程用结构钢》（GB712-2011）[8]，在此选用Q235钢，其物理力学属性见表1。

1.2 海洋环境参数与荷载设置

1.2.1 环境参数

由南海某工程实例[9]中选取本文所需的海洋环境参数如下：

波高H=6.5m，波周期T=8s，海面流速u=1.1m/s，海底高程为0m，自由液面高程为1000m。

1.2.2 荷载设置

分析对象在海洋环境中受到重力G、浮力Ff、上部荷载Fs、海流力Fh和波浪力Fw的作用。结构自重G通过输入重力加速度（g=9.8m/s2）自动施加到整个模型上。对随机波浪力Fw用采用谱分析法[10]，由已知的海浪谱推求出作用于结构物上的波浪力谱，从而确定不同累计频率的波浪力，以PSD随机集中力激励[11]的形式输入ABAQUS分析软件对结构进行波浪力的添加。除重力G和波浪力Fw之外的其余三个力均根据静力等效原则将各分力施加于相应球节点上。

1.3 网格划分

网格密度由布设在结构上的种子决定，经反复调试，对于三个部件均取全局种子密度为1。杆件网格单元形状选择Hex（六面体），即模型的网格单元均为六面体单元;球节点网格单元形状选择Hex-dominated（六面体占优），即模型主要网格单元为六面体，允许衔接区域出现三棱柱体单元。完成网格控制后，需设置网格单元类型，根据单元形状和划分技术的选择，取网格单元类型为C3D8R（三维应力单元）。

1.4 模型驗证

上述步骤完成后，提交作业，分析结束后即可查看结果。为了保证ABAQUS有限元模型在分析一榀桁架的静、动力响应时的可靠性，以进行结构优选分析，需验证有限元模型的准确性。

利用提出的有限元模型，与席石磊等人（2010）[5]进行的VLFS新型结构设计中涉及的ABAQUS软件模拟结果进行对比。其中，席石磊等人创建的模型结构几何尺寸的具体数值与本研究略有不同，但在数量级上相同，具有可比性。结构的材料属性、边界条件及荷载的施加原理等也均与席石磊等人的研究相同，将两组ABAQUS模型分析得到的静力荷载作用下的整体结构应力、应变、位移最大值以及动力荷载作用下结构各部分应力、应变、位移的最大值进行对照比较，如图2所示。

通过对照，两组模型模拟结果各项在变化趋势上基本一致。由于两组有限元模拟模型在结构尺寸上并未完全一致，故在各项模拟结果的数值上会有些许差别，但在数量级上是相同的。可以认为本研究中的ABAQUS有限元分析结果对结构在动、静荷载下的响应模拟是可靠的，其准确度可以得到保证。

2 计算结果分析

提交模型进行计算，得到了外载作用下的结构应力、应变及位移分布云图。在此规定模型所处的坐标系中x方向为纵向，y方向为横向，进行进一步的分析。

2.1 外载响应结果

结构在受到重力G、浮力Ff、上部荷载Fs、海流力Fh和波浪力Fw作用下的整体应力、应变和位移云图如图3～5所示。

由应力云图（图3）可知，一榀桁架在受外载荷作用下，应力最大值为5.521MPa，为拉应力，出现在背浪向的上层边缘腹杆接近中层球节点处。由应力值分布可知，结构整体受拉，结构上层腹杆拉应力较下层腹杆大。结构采用Q235钢，屈服应力取235MPa，考虑重力和环境荷载的组合，取安全系数为1.5，则许用应力值为157MPa，此处应力峰值为5.521MPa，结构强度满足要求。由应变云图（图4）可知，结构最大应变发生在边缘下层腹杆与中层球节点连接处，其值为0.02341。其次，桁架中层横向水平杆与边界球节点的连接处也出现较大应变，需对杆件与球节点连接处进行加强处理。由位移云图（图5）可知，桁架位移在z方向上的呈渐变性，以结构纵向中轴线为对称轴，基本呈对称分布，最大位移出现在桁架顶部边缘球节点与上部荷载接觸处，其值为0.6359mm。

2.2 自振特性分析

模型建立的第二个分析步为线性振动的频率提取分析步，计算结构自振型式及相应频率。由于结构响应往往取决于较少的几阶振型，在此运用ABAQUS有限元软件计算结构前10阶振动频率，得到的结构自振频率见表2。鉴于某些阶数的振动频率相近，在此列出一、三、五、七、八、九阶的结构振型，如图6～11所示。

随着振动频率的增大，结构应力逐渐变大，应力从0.162MPa（一阶）增大到17630MPa（十阶），远超结构的屈服应力，导致结构变形以致破坏。根据对振型观察，第一、二、三、四、七阶自振频率下的结构主要发生平向变形，结构朝一个或两个方向上产生较大位移，在此5阶频率的振动下，结构最大应力数量级均为102MPa。其余5阶频率的振型较复杂，在平向变形的同时，也在多点发生了扭转变形，使结构大幅度偏离设计尺度，丧失结构承载力。从应力响应也可看出，第五、六、八、九、十阶振型下结构最大应力数量级为104MPa，超过了结构屈服条件，导致结构变形以致破坏，不再具备承载外部荷载的能力，故处于海洋环境中的此结构应避免遇到频值为以上值的外荷载。在本研究中，波浪频率f=0.125Hz，远小于结构的危险自振频率，不会发生共振现象，结构安全。

3 结构双参数优选

为了得到特定海况下结构强度较好，受力性能更为合理的网架结构，需变化结构的各参数尺寸进行静力、动力荷载下的力学响应，考察尺寸变化对结构的应力、应变、结构位移和承载力有何影响，需要用到ABAQUS有限元软件对不同尺寸方案的网架结构进行计算分析。在海洋环境参数及整体结构尺寸确定的前提下，对三层网架高度2H、腹杆与水平面夹角α、球节点和杆件直径D（D1/D2）以及球节点和杆件壁厚T（T1/T2）这六个参数，运用同时改变两个参数，控制其他参数不变的方法进行参数优选。本研究将三层网架高度2H和腹杆与水平面夹角α作为第一组变量参数;球节点和杆件直径D1、D2作为第二组变量参数;球节点和杆件壁厚T1、T2作为第三组变量参数进行结构的参数优选，得到三组共11个结构尺寸方案如表3所示：

3.1 第一组参数优选分析

第一组参数优选方案锁定球节点和杆件直径D（D1/D2）、球节点和杆件壁厚T（T1/T2）不变，将三层网架高度2H、腹杆与水平面夹角这一参数组进行尺寸优选，4组优选方案分别为：H=12m，α=50°;H=15m，α=55°;H=18m，α=60°;H=21m，=65°。运用ABAQUS有限元软件对4组方案进行了模拟，分析得到了分析对象在静力荷载、动力荷载下结构的最大应力值，通过对结构逐级加载的方法得到了对应结构的极限承载力，并计算结构耗钢量，如表4所示。

结合数据和曲线进行分析可知，随着高度H和角度的增加，静力荷载下结构的最大应力先减小后增大;波浪荷载下结构的最大应力，即结构的最大动应力呈上升趋势，且方案3和方案4的相对应力增加值较大;结构极限承载力随方案的变化先增大后减小;结构耗钢量先降低后升高后降低，但变化趋势总体较为平稳。以上4种方案在动荷载及静荷载作用下的结构最大应力均满足设计要求。但方案1在钢耗量最大的情况下承载力并不理想，从经济成本角度考虑并不合适;方案4对动、静荷载作用的响应较为敏感，特别是在波浪荷载作用下的结构最大应力为最小值（方案1）的5倍，且结构极限承载力在前3方案均呈上升趋势，在方案4处扭转直下，故方案4也被排除。方案2和方案3在耗钢量相差不大的基础上，后者的最大静应力较方案2增加了7.5%，最大动应力虽增加了220%，但其在数值上距结构的屈服应力还有很大的富余，安全性能得到保证。方案3极限承载力较方案2增加了20.7%，故在此参数组中，取H=18m，α=60°。

3.2 第二组参数优选分析

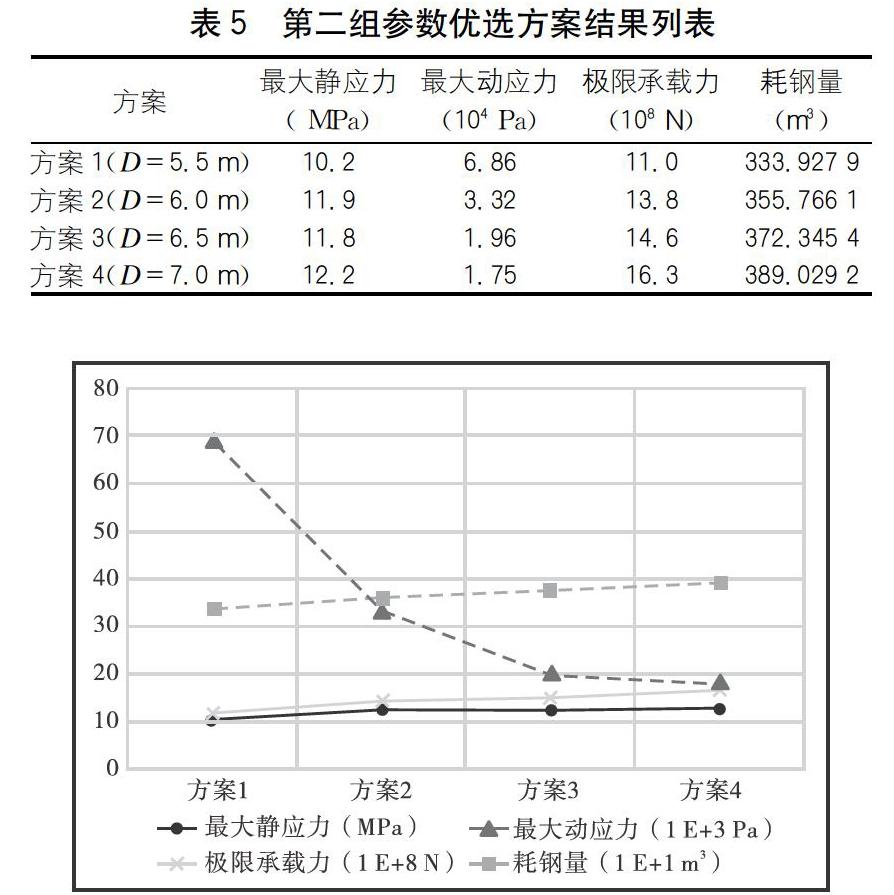
第二组参数优选方案锁定三层网架高度2H、腹杆与水平面夹角α和球节点、杆件壁厚T（T1/T2）不变，将球节点和杆件直径D（D1/D2）这一参数组进行尺寸优选。4组优选方案分别取D=5.5m、6m、6.5m、7m。分析结果及相应趋势图分别见表5和图13。

结合数据和曲线分析可知，研究对象在静力荷载作用下结构应力随着球节点和杆件直径的变大呈平稳状态，变化幅度不大。在总体上升的趋势中，方案3的应力峰值呈一个下降的拐点。在波浪力荷载下的动力响应分析中，结构最大应力随着直径D的增大而减小，且前3个方案减幅较大。结构的极限承载力随直径D值的增大而增大，但增幅较小，最大值与最小值之间相差48.2%，变化趋势较为平稳。耗钢量也随方案值的增大而增大，最大值与最小值间相差16.5%，变化趋势总体较平稳。结构在其余尺寸不变，只增大球节点和杆件直径的情况下，耗钢量必然增加，同时结构的极限承载力也得到了相应的提升。方案3与方案2、方案4相比，在相对承载力（承载力/耗钢量）相差不大的基础上（方案2为3.88，方案3为3.92，方案4为4.10），最大静应力取得最小值为1.19N×107;且在减小结构对动力的响应方面效果较好，[JP+1]与最大值相较减少了71.4%，与方案2相较减少了41.0%。经综合分析，在此参数组中，取D=6.5m。