基于随机游走算法的建筑工地人员施工通道安全优化设计

何光辉

上海建工集团股份有限公司 上海 201114

随着我国经济建设水平的提高，建筑工程项目不论是数量还是单体规模均取得了巨大的成就。然而，随着建筑工程施工体量规模的增长，施工现场各类机械、临时和永久性设施错综复杂、施工人员素质水平良莠不齐等因素，不仅使建筑工程施工现场人员安全风险显著增加，而且也增加了项目管理人员的工作量和管理难度。

建筑施工中有关安全事故控制的成本投入回报率往往不具备直观可见和迅速见效的特点[1]，我国施工单位和建设单位在这方面的资金投入占项目总成本的比例往往较低，因此，短期内低成本或无成本的安全管控技术尝试和研究更具现实意义。为了展开建筑工地人员安全状态评估，张文博等[2]结合层次分析法和模糊综合评价法，建立了建筑施工人员安全风险评估的人工神经网络模型；林陵娜等[3]基于系统动力学提出了建筑施工项目安全状态识别模型构建方法；唐鹏等[4]结合建筑工程施工实际，考虑控制和监测措施、事故发生频率以及事故损失，建立MLS法评价施工环境危险度。王旭峰等[5]利用结构方程模型（SEM）研究建筑工人个体安全能力与影响因素间的效用关系，从个体特质和工作环境两方面进行分析，研究了影响施工人员安全的多方面因素。冯超[6]得到了超高层建筑施工安全风险评价指标体系和风险评价模型，并且对实际工程项目进行了具体分析和评价，确定施工风险等级。

在建筑施工现场，人为划定工作人员通道是行业内较为严谨的、保证施工人员安全和施工品质控制的措施之一。传统的施工通道布置主要借助主观经验的方法确定，这种做法往往不能保证人员受到施工安全风险的最小化。为此，本文借助前人得到的风险评价方法量化建筑工地各类风险源对象，综合考虑施工现场各类工作人员在各类风险区域通行时的风险程度、施工禁区、障碍物分布、建筑工地边界、出入口位置等因素，利用随机游走优化算法[7]，自动搜索建筑工地最佳的人员通道，从而将全体人员的施工风险降至最低。

1 风险量化指标

为便于利用优化算法对建筑项目施工人员的安全风险进行评估，从而建立数值优化目标函数与约束条件，施工风险的量化是不可避免的课题。昝彦国等[8]尝试应用序关系法确定安全风险源的权重指标，便于施工安全风险的动态识别与定量表示。Zhou等[9]借助Pajek软件，基于网络理论对建筑施工现场各风险之间的耦合关系进行了量化研究，从而得出了特定具体风险系统中各成员的风险因子。本文借助网络理论和历史同类风险事故的统计数据，确定建筑施工现场主要风险源对象的事故发生概率统计值，以此为基础，通过合理布置施工通道线路实现施工人员风险发生率的最小化。

2 随机游走算法

2.1 算法原理

建筑工地人员通道可能的布置方案是近乎无穷的。在现实当中，管理人员主要依据经验制定施工通道路线。这样的路线一般不会是最差的，但也很难做到最佳。为了实现最佳方案的制定，数值优化方法是强有力的理论工具。随机游走算法是一类全局优化算法，其实现过程不依赖目标函数的变化梯度。图1给出了随机游走算法的实现流程。该算法流程在各领域均得到了成功应用和良好效果。

图1 连续优化变量的随机游走算法

2.2 离散随机游走

为描述建筑工地风险与施工从业人员可能的通行路线，图2将建筑工地平面按照一定的间距做格栅划分。每一个格栅线为建筑工人允许行走的通道。假设人员处于图3所示的任一格栅节点O处，那么人员允许的行走路线为OA、OB和OC三种。为便于计算，设OA为向量（0,-1），OB为向量（1,0），OC为向量（0,1）。假定沿途所经区域具有风险属性，并且以颜色表示（表1）。

图2 建筑工地风险与障碍分布

图3 路线节点处随机游走示意

表1 建筑工地风险图例

紫色风险值取值无穷大inf，表示该区域为障碍物，不得通行，该取值具有惩罚系数的数学意义。从黑色到绿色的风险取值均根据历史同类型建筑工地风险事故数据和网络理论分析而得。此外，为控制随机游走的建筑从业人员不得跨越建筑工地边界，这里将处于建筑工地边界的节点风险值设定为无穷大。

基于上述假定，本算法的优化变量x可以为每一个节点处的行走向量OA（0,-1），OB（1,0）或者OC（0,1），在满足障碍物约束和场地边界约束的条件下，还需满足出口与入口之间的位置关系，即所有节点的行走向量之和为出入口节点构成的向量。由于每个节点以及相邻的节点具有相同的风险属性，故人员从入口到出口沿途经过的节点风险属性值累积量即为优化目标函数。为了继续使图1所示的随机游走优化算法在路径优化问题中有效，仅需要将其中一个环节做调整：将生成的随机矩阵修正为每个元素为（0,-1）、（1,0）或（0,1）的随机向量；此外，还需要添加惩罚项作为约束条件，如边界处和障碍物处的节点风险值取为大数，如106。这样，随着优化算法的执行，游走路径一旦接触惩罚点，程序即可躲避该点。显然，这种方法可以实现优化目标函数的约束施加。

3 算例分析

3.1 施工现场

为了采用随机游走算法实现某建筑工地的施工通道优化设计，对图2所示场地进行计算分析。

这里，东西方向和南北方向格栅间距均为1 m。当然，间距也可以更小，有助于提高计算精度。设定建筑工地的风险取值如表2所示。

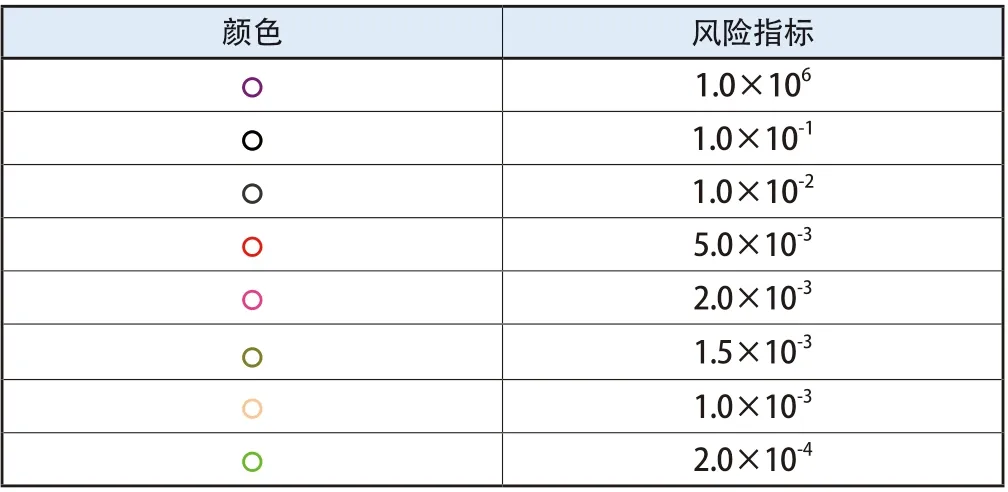
表2 某建筑工地风险取值

3.2 随机游走分析

为了进行上述分析，我们采用Julia语言进行了程序开发，在配置为Windows 10 x64操作系统，Intel i7 8700k CPU的台式计算机中进行了优化分析。设定计算误差ε为10-5；迭代次数N＝100；初次步长λ为3。优化初始路径为图4所示估计路径。所有路径的前进向量之和为（出口-入口）之坐标差，即（35,13）。

图4 建筑工地施工通道优化分析初始路径

优化分析程序经过18.53 s的优化分析，路径迭代更新为图5中蓝色实线，表示优化所得施工通道路径。施工人员沿图5所示施工通道行走的风险值为0.2292。由于算法假定了人员通道只能沿着格栅前进和左右拐，因此，分析路径只能为折线状。

为了便于实际应用，在建造中，可以将其进行做倒角或倒圆等光滑处理，如图6所示。

图5 建筑工地施工通道优化分析结果

图6 光滑处理后的施工通道

图6所示的最终所得的建筑工地人员安全通道满足了所有障碍物约束和施工场地围栏的约束。优化程序通过反复试算与更替，得到了风险最小的通道路线。

有关风险的取值问题主要受到各颜色风险打分的限制，但事实上本文算法中各颜色风险的取值绝对值并不影响最终优化结果，只要各风险源之间的风险相对值接近客观事实即可。这一点也降低了工程管理人员对风险指标的取值难度。

4 结语

利用网络理论和建筑工地历史事故数据，总结得到建筑工地现场的各风险源指标。而后，本文将运筹学中较为成功的随机游走数值最优化技术应用于建筑工程现场人员安全风险控制问题，提出了一种能降低建筑工地施工通道安全风险、高效且“无成本”的方法。基于提出的算法和计算机程序，对某建筑工地进行了施工通道选线优化分析，所得结果表明本文方法具有较强的可实践性，可作为今后同类型问题分析的一种参考。

[1] 李志鹏.超高层建筑施工安全管理研究:以某超高层建筑为例[D]. 武汉:湖北工业大学,2017.

[2] 张文博,宋德朝,郑永前.基于神经网络的建筑施工安全评价[J].工 业工程,2011,14(2):75-79.

[3] 林陵娜,苏振民,王先华.基于系统动力学的建筑施工项目安全状态 识别模型构建[J].中国安全生产科学技术,2011,7(12):2011.

[4] 唐鹏,唐莉,孟宪强.建筑施工人员安全度评价模型的构建与应用 [J].中国高新技术企业,2010(33):64-66.

[5] 王旭峰,邱坤南,阳富强,等.建筑工人个体安全能力影响因素效用量 化研究[J].中国安全科学学报,2015,25(3):133-139.

[6] 冯超.超高层建筑工程施工安全风险评价[D].长沙:中南大学,2013.

[7] 孙慧影,林中鹏,刘银丽,等.基于随机游走蜂群算法优化RBF神经网 络电动机故障诊断研究[J].水电能源科学,2017,35(8):165-168.

[8] 昝彦国,侯学良.建筑施工阶段动态识别安全风险的指标体系构建 [J].建筑经济,2016,37(3):102-105.

[9] ZHOU Z, IRIZARRY J, LI Q. Using network theory to explore the complexity of subway construction accident network (SCAN) for promoting safety management[J].Safety science,2014(64):127-136.