基于贪心算法的智能RGV的动态调度策略

李胜成

摘  要：一种智能加工系统由8台计算机数控机床（CNC）、1辆轨道式自动引导车（RGV）、1条RGV直线轨道、1条上料传送带、1条下料传送带等附属设备组成。文章通过研究RGV的选择判断规律，以一道工序无故障情况为例，在RGV需要选择去向时采用贪心算法，这体现为RGV每次选择去向时选择运动时间与上下料时间之和最小的目标，将该过程定为所有判断的原则。故可得出动态调度后每个CNC的总等待时间最少，将机床工作效率最大化。从而给出最优动态调度策略。

关键词：动态调度;贪心算法;灵敏性分析

中图分类号：O221 文献标志码：A         文章编号：2095-2945（2020）06-0016-02

Abstract： An intelligent machining system consists of 8 computer numerical control （CNC） machine tools， 1 rail guide vehicle（RGV）， 1 RGV linear track， 1 feeding conveyor belt， 1 cutting conveyor belt and other ancillary equipment. In this paper， the selection and judgment rule of RGV is studied. Taking a working procedure with no fault as an example， greedy algorithm is adopted when RGV needs to select the direction， which is reflected in the minimum sum of movement time and loading and unloading time when RGV selects the direction， and this process is set as the principle of all judgments. Therefore， it can be concluded that the total waiting time of each CNC after dynamic scheduling is the least， and the working efficiency of the machine is maximized. The optimal dynamic scheduling strategy is given.

Keywords： dynamic scheduling; greedy algorithm; sensitivity analysis

1 概述

对智能加工系统建立RGV动态调度模型[1]，需使用

matlab软件编程，通过判断语句和循环语句实现RGV的状态转换和系统时间的推进，程序模拟的信息世界变量转换要遵循现实世界不同情况下物体运行规律，通过matlab程序仿真实现过程和结果的输出，并通过优化RGV工作状态转换原则来改善动态调度模型。

2 一道工序无故障情况

2.1 模型的建立

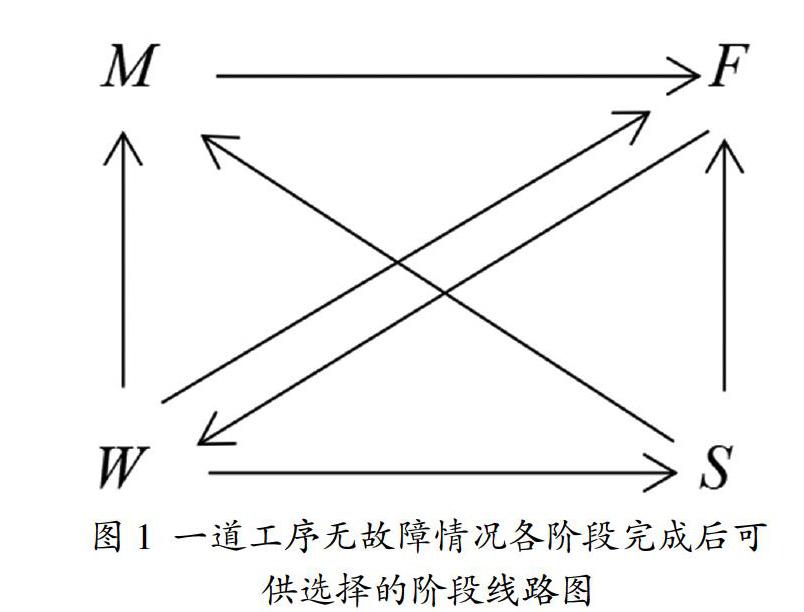
RGV具有的四个工作阶段为：移动阶段M、上下料阶段F、清洗阶段W、停止阶段S[2]。

通过附件一所给系统作业流程，可总结出在一道工序无故障情况下各阶段完成后可供选择的阶段线路图（如图1所示），系统总运行过程应由若干该子图拼接而成。

RGV的移动阶段M后必定为上下料阶段F，上下料阶段F后必定为清洗阶段W，这两个阶段不需要进行判断。RGV在清洗阶段W后有两种可能的情况：

（1）完成清洗阶段的时间点没有需求信号，RGV进入停止阶段。

（2）若此时有需求信号，根据此时RGV的位置和信号位置判断，又分为以下两种情况：

若此时RGV与需求信号在同一列上，即可直接进行上下料工作。

若此时RGV与需求信号不在同一列，通过判断决定接下来移动的方向与距离。

智能加工系统通电后，RGV位于CNC1和CNC2正中间的初始位置，所有CNC都处于空闲状态。故RGV的第一步应为对所有CNC进行上料操作。我们发现上料侧CNC一次上下料所需时间明显小于下料侧CNC，故优先对上料侧CNC进行上料操作，则对CNC初始上料操作的先后顺序如图2所示。

在此基础上，我们利用贪心算法[1]，建立一道工序无故障情况下RGV动态调度模型。

貪心算法是指在对问题求解时，总是做出在当前看来是最好的选择，也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。故我们通过确定各个子阶段的局部最优解来进行RGV的动态调度，即在RGV的清洗阶段W和停止阶段S完成后接收到物料已完成信号时进行动态调度。[3]

该动态调度的决策仅考虑当前情况且该决策无后效性。设某时刻RGV的位置为X0，RGV在该时刻同时接收到m个已完成信号，此时RGV进行去向判断，判断方法应为RGV到达该点的移动时间与上下料时间之和最小。设第p个已完成信号的横向位置为xp，则该信号与RGV的距离i=X0-xp，即本次移动时间为tMi=t，RGV为该CNC一次上下料的时间为tFp=tF奇，上料侧CNC

tF偶，下料侧CNC。则RGV下一步的去向应为当tM+tF=mint+tFp时信号的发出地，子流程的决策完成。

基于该去向判断方法可知，当优先于某物料下料的物料数为s，则一个CNC完成一个物料所需的等待时间twait=mint+tFp。当一个CNC八小时一共完成了n个成料和n'个半成品物料时，该CNC所需的总等待时间T为：

该情况下动态调度原则为每个CNC的总等待时间最少：

T=min

设tr为第r次上下料开始时间点，则tr+1表示第RGV执行上下料操作开始的时间点，他们之间相隔时间至少为：一次上下料时间+加工时间+清洗时间+移动时间，可用该递推式表示tr+1?tr+tF1+tP+tW+tM。

各CNC八小时总工作过程的约束条件为：

其中n'为平均每个CNC完成的半成料数量。

2.2 模型的求解

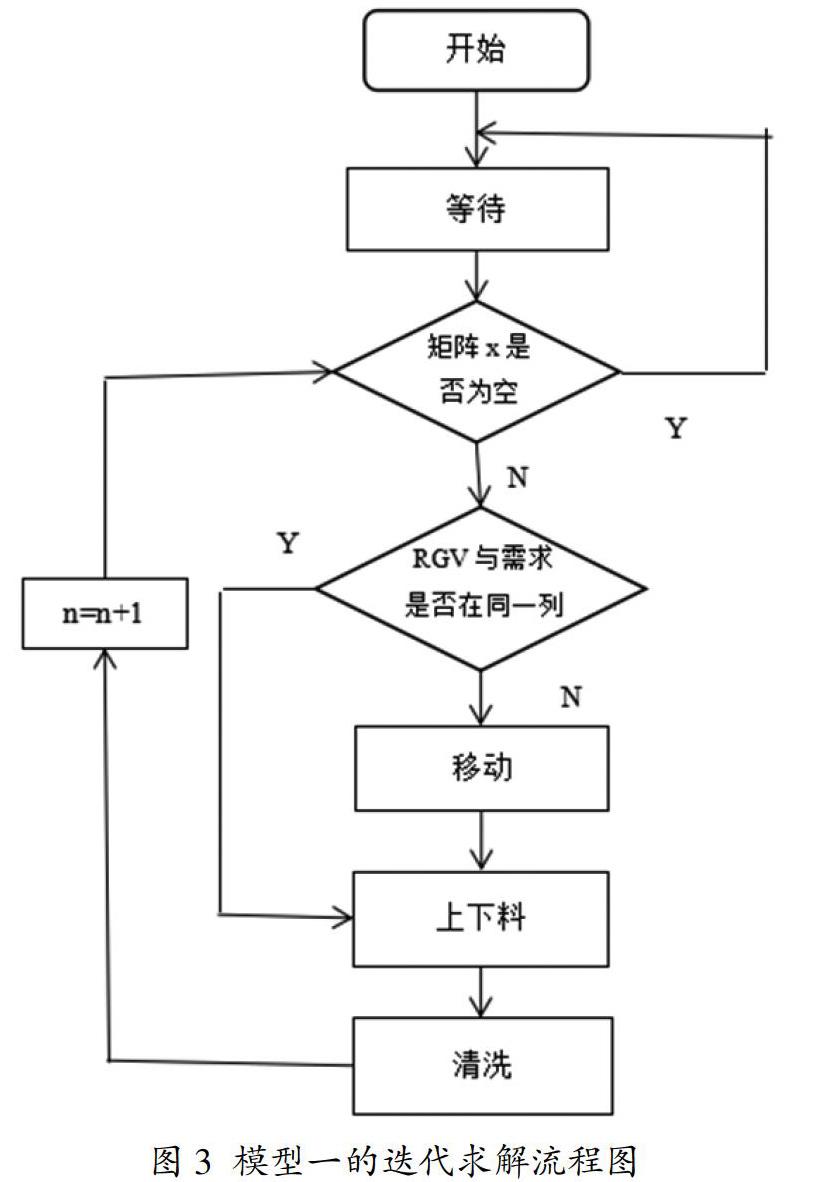
定义一个需求矩阵[x]2×4，元素为0表示物料无下料需求，1表示有下料需求。在初始上料完成后[x]2×4为全0矩阵。n为完成的成料数，初值为0。迭代求解程序流程图如图3所示：

最终可求得当程序内的总时间到达八小时后，成料数n及各物料的上、下料时间。

3 结束语

本文针对一道工序的情况，建立了基于贪心算法的数学模型，并且利用matlab[4]求解了该模型。经过该方法调度后每个CNC的总等待时间最少，从而效率将最大化。对生产实际具有一定的借鉴作用。

参考文献：

[1]周正昱.智能RGV的动态调度策略模型[J].南方农机，2018（23）：55-56.

[2]董军军.动态规划算法与贪心算法的比较与分析[J].软件导刊，2008（02）：129-130.

[3]王建玲，齐紫茜，何璐.基于蚁群算法的车辆调度问题[J].交通科技与经济，2014，16（6）：37-39，94.

[4]卓金武，等.MATLAB在数学建模中的应用[M].北京：北京航空航天大学出版社，2011.