普特南数学竞赛的历史与启示——一项实证研究

牛伟强何忆捷熊 斌

普特南数学竞赛的历史与启示——一项实证研究

牛伟强1，何忆捷2，3，熊 斌2，3

（1．郑州师范学院 数学与统计学院，河南 郑州 450044；2．华东师范大学 数学科学学院，上海 200241；3．上海市核心数学与实践重点实验室，上海 200241）

调查研究1938—1978年普特南数学竞赛优胜者——普特南会员的职业发展情况发现：大多数（76.4%）普特南会员都会获得博士学位，并且获得的博士学位几乎全部都是理工科博士学位，特别是数学（含统计学）博士学位；大多数（77.0%）普特南会员都会选择科学研究和教学作为自己的职业，特别是从事理工类科学研究和教学工作；多数（60.9%）普特南会员都会选择成为一名数学家，在高等院校或科研机构从事数学教学和研究工作；普特南会员的性别差异极为显著，40年间没有一位女性成为普特南会员．数学竞赛是识别和选拔数学与科学研究人才的有效途径．

普特南数学竞赛；普特南会员；科学家；数学家

1 引言

现代数学竞赛起源于1894年的匈牙利，其后一些国家开始效仿．第一届国际数学奥林匹克竞赛（International Mathematical Olympiad，简称IMO）于1959年在罗马尼亚正式举行，比赛吸引了欧洲不少国家参加，是为国际数学竞赛的开端[1]．随着国际数学奥林匹克竞赛的影响日益扩大，参加比赛的国家越来越多，数学奥林匹克竞赛逐渐走进世界各国．截止2018年初，国际数学奥林匹克竞赛已经举行了58届，中国自从1986年正式派代表队参赛以来，取得了举世瞩目的成绩，引起了社会各界的广泛关注．

随着数学竞赛在中国的快速发展，数学竞赛教育也出现了不少乱象，从而引起了一些社会人士和媒体的批评，就连教育界对数学竞赛也产生了分歧．许多学者相继发文对数学竞赛及其教育提出异议，甚至有学者对数学竞赛的教育价值也提出了质疑[2-4]．例如，周玲在“数学竞赛在中国的实践质问其教育价值”一文中声称：“数学竞赛扼杀了大多数青少年学习数学的兴趣，阻碍了大多数青少年全面健康地发展，选拔不出真正的数学人才，未能有效促进中学数学教学改革，甚至还提出了‘数学竞赛是否适合中国？’这样的疑问．”[2]尽管已经有不少学者从理论的角度论述了数学竞赛的教育价值[5-8]，但是相关的实证研究仍然较为欠缺，类似文[9]这样基于证据的研究很是罕见．实证研究的匮乏不利于人们充分地认识数学竞赛及其教育价值，更不利于人们正确地面对数学竞赛．因此，很有必要从实证的角度进一步深入探讨数学竞赛及其教育价值．

数学竞赛能否较为准确地识别和选拔出最有潜力和最有希望的数学和科学研究后备人才是一个重大的研究课题．目前，关于数学竞赛优胜者与科学家和数学家关系的研究主要是通过列举一些后来成名的数学家或科学家来加以说明[1，7，10]．然而，个别数学竞赛优胜者的成功并不能表明数学竞赛优胜者作为一个群体都能取得成功．研究者认为要回答这个问题，最好的方法就是调查某一数学竞赛所有优胜者的职业发展情况，分析数学竞赛优胜者究竟有多大的比例能够成为科学家特别是数学家．事实上，尽管国内外知名的数学竞赛并不少，如国际数学奥林匹克竞赛、中国数学奥林匹克竞赛，等等，然而人们关心的大多是竞赛选手的获奖情况以及竞赛试题情况，很少有学者关注数学竞赛优胜者的职业发展情况．特别地，关于数学竞赛优胜者职业发展系统且完整的统计信息极为罕见，但普特南数学竞赛的优胜者——普特南会员是个例外．

普特南会员是由美国数学协会授予普特南数学竞赛前5名的荣誉称号．普特南数学竞赛始于1938年，是为了纪念美国律师和银行家威廉·洛韦尔·普特南（William Lowell Putnam，1861—1923）而举办的，参赛对象是美国和加拿大高等院校数学系的学生，其目的在于鉴别出美国和加拿大最优秀和最有潜力的数学后备人才[11]．截止2018年初，除了第二次世界大战的3年（1943—1945）外，普特南数学竞赛已经连续举办了78届，成为世界上最具影响力的一个大学生数学竞赛活动．美国明尼苏达大学（德卢斯）【University of Minnesota (Duluth)】已经建立了普特南会员职业发展路径追踪网站，通过这个网站基本可以查询1938年以来所有普特南会员的职业发展情况[12]．鉴于此，研究者设想以普特南会员作为数学竞赛优胜者的代表，通过追踪普特南会员的职业发展路径来探寻数学竞赛优胜者与科学家特别是数学家的关系．

2 方法

2.1 概念界定

科学家是从事科学研究的人，是科学知识的培育者、耕耘者、发明者或发现者[13]．科学家根据研究领域的不同大致可以分为两类：理工类科学家和人文社科类科学家．理工类科学家指的是从事理学或工学研究与教学工作的专业工作人员；人文社科类科学家指的是从事人文科学或社会科学研究与教学工作的专业工作人员．尽管在科学史上既从事理工类科学研究又从事人文社科类科学研究的学者并不鲜见，这里根据科学家最主要的研究领域进行划分．在理工类科学家中有一大批研究人员是数学家．根据数学家在数学研究中取得的成就可以把数学家分为3类：杰出数学家、优秀数学家和普通数学家．杰出数学家指的是在高等院校或科研院所从事数学教学与研究工作不仅获得教授职位而且当选科学院院士（Member of National Academy of Science）或者获得菲尔兹奖（Fields Medal）的专业工作人员；优秀数学家指的是在高等院校或科研院所从事数学教学与研究工作并且获得教授职位的专业工作人员；普通数学家指的是在高等院校或科研院所从事数学教学与研究工作但没有获得教授职位的专业工作人员．

2.2 数据处理

1938年以来普特南数学竞赛产生了数以百计的普特南会员．那么，应该选取哪些普特南会员进行研究呢？研究者认为评价一位科学家的职业成就应该等到科学家到达职业的顶峰．然而，判断一位科学家何时达到职业的巅峰是一件十分困难的事情．鉴于此，研究者认为等到科学家退休之后再评价其职业成就将是一个较好的选择．目前，中国科研人员的退休年龄一般是60岁．普特南数学竞赛的参赛选手一般在20岁左右，而1978年的普特南会员目前刚好60岁左右，恰好到了退休的年龄．据此，研究者认为对1978年及以前的普特南会员能较好地评价其职业成就．最终，研究者决定选取1938—1978年的普特南会员作为研究对象，利用二手资料分析法，从博士学位、科学家类型、数学家类型以及性别差异4个角度统计普特南会员的百分比，对普特南会员的职业发展进行分析．对于信息不完整者，借助维基百科对每一位普特南会员的职业发展情况进行补充，同时借助数学家谱项目对每一位获得数学博士学位的普特南会员进行核实[14]．

3 结果

1938—1978年一共举行了39届普特南数学竞赛，每届竞赛一般产生5名普特南会员，成绩相同的时候例外．普特南会员最多的时候是1959年，共有9名，原因是第五名有5人成绩相同．最后，统计发现1938—1978年普特南数学竞赛一共产生了161位不同的普特南会员．

3.1 普特南会员的博士学位情况

在世界各国的教育体系中，博士都是最高级别的学位，获得博士学位通常标志着一个人具备了独立从事相关学术研究的能力．因此，一般来说，科学研究工作者都要具有博士学位．在现代社会要成为一名科学家基本都需要接受系统的学习和训练，特别是经过博士阶段的学习并获得博士学位．据此，研究者对1938—1978年的普特南会员获得博士学位的情况进行了调查，结果见图1．

根据图1，可以发现1938—1978年的普特南会员中有105人（65.2%）获得数学（含统计学）博士学位，有15人（9.3%）获得物理学博士学位，有2人（1.2%）获得计算机科学博士学位，获得历史学博士学位的有1人（0.6%），没有获得博士学位的只有38人（23.6%）．一共有123人获得博士学位，占全部161位普特南会员的76.4%．需要注意的是，除了一位普特南会员得到的是历史学博士外，其他普特南会员获得的都是理工科博士学位，并且在博士学位获得者中获得数学（含统计学）博士学位的普特南会员占了绝大多数（85.4%），几乎达到了全部普特南会员的三分之二．由此可见，普特南数学竞赛的优胜选手中大多数普特南会员都会获得博士学位，并且获得的博士学位几乎都是理工科博士学位，特别是数学（含统计学）博士学位．

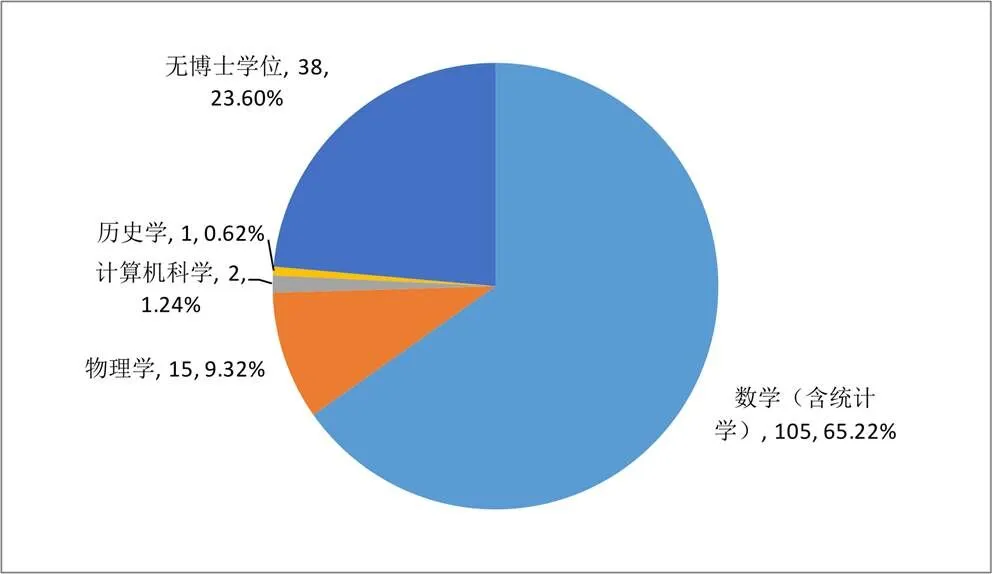
图1 普特南会员的博士学位情况

3.2 普特南会员与科学家的关系

科学家在人类社会进步过程中发挥着关键的作用，尽管杰出科学家在科学家群体中仅占微不足道的数目，然而他们在科学中的地位却举足轻重，正是他们能极大地加速科学进步的步伐[13]．因而，科学家特别是杰出科学家的培养一直是世界各国教育界关心的核心话题．根据前面对科学家的界定和分类，研究者对1938—1978年普特南会员的职业发展情况进行了分类，结果见图2．

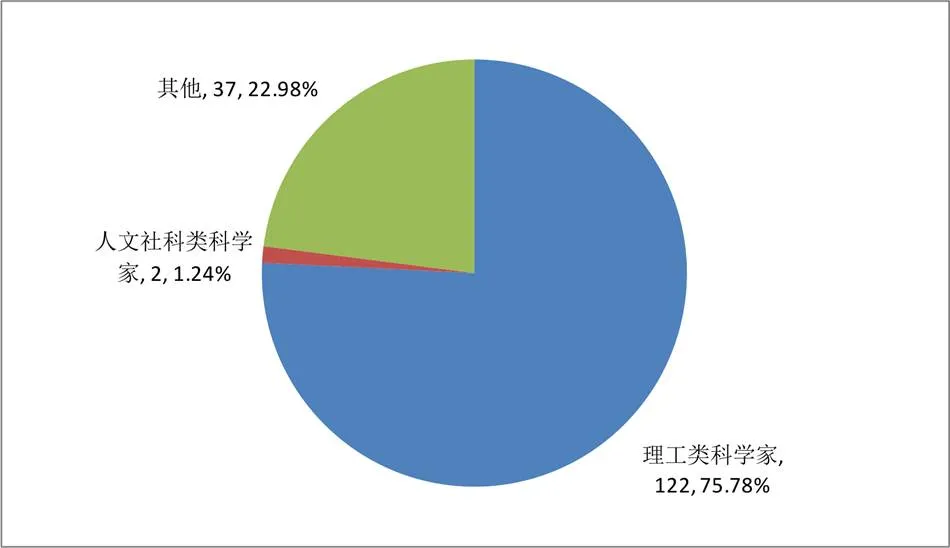
图2 普特南会员成为科学家的情况

根据图2，可以发现1938—1978年的普特南会员，在其职业生涯中最终成为理工类科学家的有122人（75.8%），成为人文社科类科学家的有2人（1.2%），选择科学家作为职业的一共有124人，占同期161位普特南会员的77.0%．没有选择科学研究作为自己职业的普特南会员只有37人，占23.0%．可见，普特南数学竞赛的优胜选手中大多数普特南会员职业选择时都选择了成为科学家，特别是理工类科学家，以在高等院校或科研机构从事科学研究和教学作为自己的终身职业．究其原因，可能在于普特南会员大多拥有良好的数学素养，从事数学研究或者从事理工类相关的科学研究成为大多数普特南会员职业倾向的必然选择．另外，研究者还发现这161位普特南会员中当选科学院院士或获得菲尔兹奖或诺贝尔奖的杰出科学家一共有17位，占同期161位普特南会员的10.6%．可见，普特南会员中涌现出杰出科学家的概率极高．

3.3 普特南会员与数学家的关系

随着时代的发展，数学不仅渗透到自然科学，社会科学也在数学化．因此，数学研究及其应用人才的培养引起了世界各国的高度重视．通过对普特南会员博士学位情况的分析，研究者发现大多数普特南会员都会拿到理工科博士学位，并且将近三分之二的普特南会员都会获得数学博士学位．那么普特南会员将来是否会成为数学家呢？为了回答这个问题，研究者根据前面对数学家的分类对1938—1978年普特南会员的职业发展情况再次进行了分析，结果见图3．

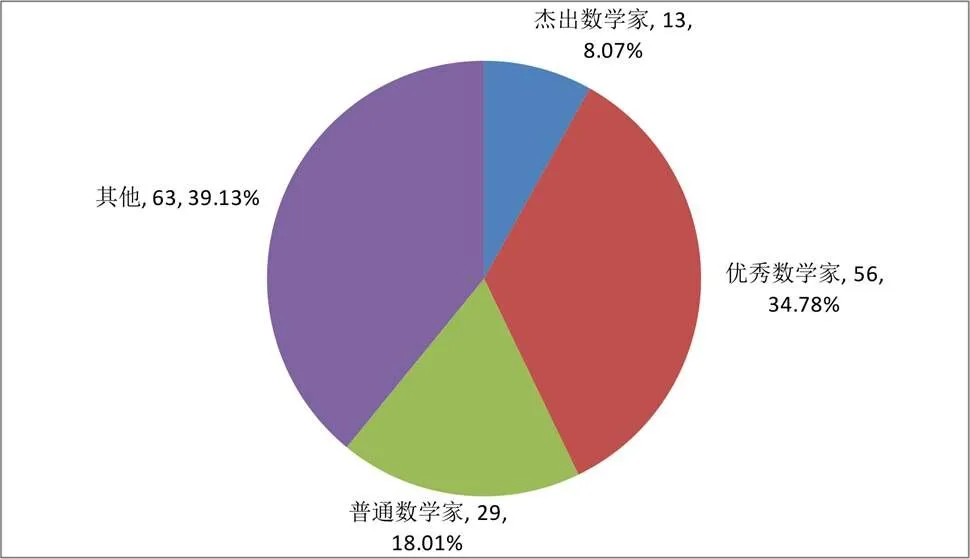
图3 普特南会员成为数学家的情况

根据图3，可以发现1938—1978年的普特南会员，在其职业生涯中一共有13位（8.1%）普特南会员成为科学院院士或者获得菲尔兹奖，成为杰出数学家；此外，还有56位（34.8%）普特南会员也获得了教授职位，成为高等院校或者科研院所的优秀数学家；最后，还有29位（18.0%）普特南会员在高等院校或者科研院所从事数学教学和研究工作．在高等院校或科研机构从事数学教学和研究工作的普特南会员一共有98人，占同期161位普特南会员的60.9%，没有从事数学教学和研究工作的普特南会员只有63人，仅占39.1%．可见，普特南数学竞赛的优胜者中多数普特南会员都选择了成为一名数学家，在高等院校或科研机构从事数学教学和研究工作．分析原因，可能是由于多数普特南会员本身对数学持有强烈的兴趣，对从事数学教学和研究工作意志坚定，职业志向成为一名数学家．

3.4 普特南会员中数学家的性别

性别是教育研究中的重要变量，个体在教育方面表现出来的许多差异都与性别有关，不少差异甚至可以归因于性别的不同．数学史研究发现，历史上有记载的数学家特别是成绩斐然的数学家大多数都是男性，而女数学家特别是杰出的女数学家极为罕见．因此，数学教育中的性别差异问题引起了国内外学者的广泛关注，性别差异也一度成为国际数学教育研究的一个热点话题．鉴于此，研究者对1938—1978年普特南会员的性别差异进行了调查和统计，结果见图4．

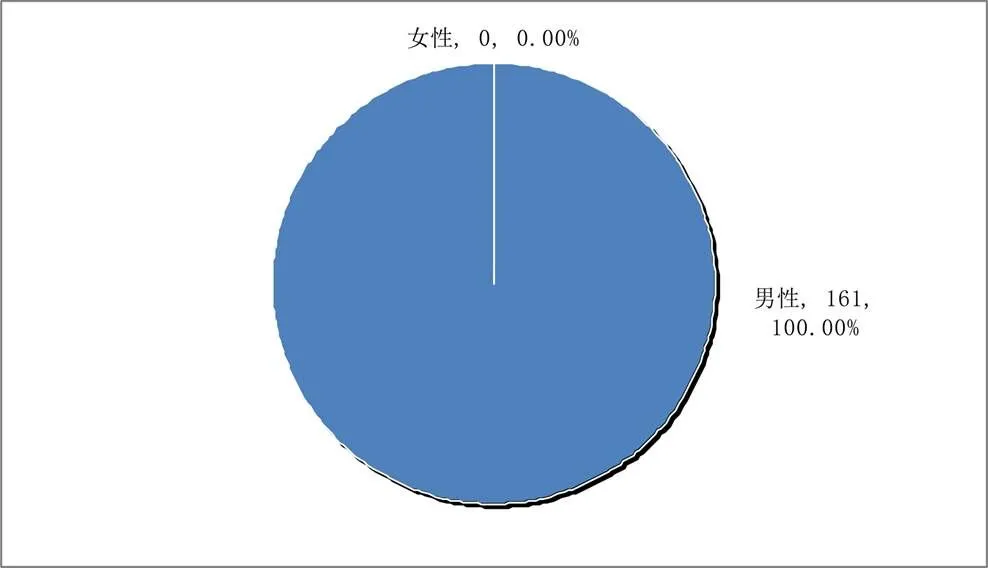
图4 普特南会员的性别差异

根据图4，可以发现1938—1978年所有161位普特南会员全部都是男性，40年间没有出现哪怕一位女性普特南会员，更不要说产生女科学家、女数学家了．换句话说，也就是这40年间的普特南数学竞赛的参赛选手中没有一位女性能够进入普特南数学竞赛前5名．这个结果是令人震惊的．尽管不少研究发现数学教育中存在一定的性别差异，但是普特南会员的性别差异竟然如此的悬殊，仍然不免令人大吃一惊．由于研究过程中使用的是第二手资料，它并没有提到任何普特南数学竞赛参赛选手的性别构成和比例问题，并且现在探讨1938—1978年普特南数学竞赛参赛选手的性别问题几乎是一件不可能的事情．因此，对于其中的原因目前尚无法确定．

4 结论

调查了1938—1978年普特南数学竞赛优胜者——普特南会员的职业发展情况，探讨了普特南会员与科学家特别是数学家的关系，得到如下结论：

（1）普特南数学竞赛的优胜选手中大多数（76.4%）普特南会员都会获得博士学位并且获得的博士学位几乎全部都是理工科博士学位，特别是数学（含统计学）博士学位．

（2）普特南数学竞赛的优胜选手中大多数（77.0%）普特南会员都会选择科学研究和教学作为自己的职业，特别是从事理工类科学研究和教学工作．

（3）普特南数学竞赛的优胜选手中多数（60.9%）普特南会员都会选择成为一名数学家，在高等院校或科研机构从事数学教学和研究工作．

（4）普特南数学竞赛的优胜选手中普特南会员的性别差异极为显著，40年间没有一位女性成为普特南会员．

5 启示

5.1 数学竞赛的教育价值不容忽视和否认

1938—1978年普特南数学竞赛的优胜者——普特南会员中的大多数（77.0%）人都能够成为科学家特别是数学家，普特南会员中涌现出杰出科学家或数学家的比例（10.6%）更是相当惊人．可见，普特南会员作为一个群体，其成才率非常高．毫不夸张地说，普特南数学竞赛成功地识别出一大批极具潜力的数学和科学研究后备人才．这充分表明数学竞赛是识别和选拔数学与科学英才的有效手段．因此，数学竞赛的教育价值不可忽视，更不容否认．虽然在中国数学竞赛教育发展的过程中出现了一些不恰当的做法，但据此批判甚至否定数学竞赛的教育价值则有失公允．研究者认为目前应该做的不是批判和否定数学竞赛而是完善和规范数学竞赛，使数学竞赛教育真正成为资优生的成功和成才之路．

5.2 数学竞赛优胜者不一定会成为数学家

尽管调查发现1938—1978年普特南会员中的多数人（60.9%）都能够成为数学家，但是还有一部分（16.1%）普特南会员没有成为数学家，而是在从事其它科学研究和教学工作，他们的职业以物理学、计算机科学等理工类工作为主，最后还有大约23.0%的普特南会员并不从事科学研究与教学工作．这些事实充分表明数学竞赛优胜者的职业发展是多样化的．数学竞赛优胜者的职业以理工类工作为主，但不一定非要是数学家．那种认为数学竞赛优胜者一定要成为数学家的想法是荒唐的，也不符合实际．最后，中学数学竞赛优胜选手职业发展的不确定因素更多，中学数学竞赛优胜选手很有可能更多地不从事数学和科学研究工作．因此，中学数学竞赛优胜选手成为科学家特别是数学家的比例可能还要低一些．

6 建议

6.1 建立长期的英才生跟踪机制

1956年在华罗庚等一批著名数学家的倡议下，北京、上海等城市开始举办中学生数学竞赛．尽管中国举办中学生数学竞赛并不晚，但是竞赛优胜者的职业发展记录却极为罕见，并且基于证据的数学竞赛对中小学生影响的实证研究也很少见．究其原因，可能是中国的数学教育研究者很少亲自参与到数学竞赛的第一线，而一般的数学竞赛教练也缺乏相关的教育研究方法和经验．因此，加强数学教育研究者与数学竞赛教练的合作极为必要和迫切．普特南会员的职业发展已经建立了相关的网站，这使得对普特南会员进行长期的跟踪研究成为可能．然而，关于中国英才生特别是数学英才生的长期研究却极为罕见，一个最主要的原因可能就是缺乏长期的统计数据．因此，研究者强烈建议建立数学英才生和数学竞赛优胜者档案，建立长期的英才生跟踪机制，并对英才生进行长期的追踪研究，这对深刻认识和研究英才生的成长、成才规律极为有利和必要．

6.2 加强数学英才生的教育研究

数学竞赛本身的目的是发现最有天赋和最有潜力的数学后备人才，而后备人才成长为真正的科学家还要受到许多其它因素的影响．尽管研究表明数学竞赛是识别和培养数学与科学英才的重要途径，但数学英才教育并不仅限于数学竞赛，大学数学先修课程、专家个别辅导也是数学英才教育的重要方式．然而，中国数学英才教育这些方面的研究却很是匮乏．数学竞赛不是大众教育，而是针对少数数学英才学生的一种英才教育[15]．因此，数学竞赛教育的目的不是为了获奖，而应该是发展学生的数学思维能力，发掘学生的数学潜能．然而，不幸的是，中国数学英才教育由于各种因素的影响，功利主义、拔苗助长等不良倾向极为普遍．在一项关于数学英才教育的研究述评中更是发现，中国数学英才教育与美国等世界数学强国相比显得较为单一和薄弱，在数学英才的教育方面还存在较大差距[16]．因此，数学英才生的教育亟待数学教育研究者探索和研究．

6.3 明确大学生数学竞赛的目标

普特南数学竞赛是针对数学系大学生的纯数学的纸笔考试，主要考察在限定的时间内参赛者的创造性、推理能力和计算能力，目的在于鉴别出美国和加拿大最优秀和最有潜力的数学后备人才[11]．可见，普特南数学竞赛的目标十分明确，那就是发现美国和加拿大最有天赋和最有潜力的数学后备人才，为培养一流的数学家或科学家提供人才储备．事实上，普特南数学竞赛确实实现了预期的目标，普特南数学竞赛的优胜选手后来涌现出一大批杰出的数学家和科学家．中国大学生数学竞赛举办较晚，直到2009年首届中国大学生数学竞赛才由国防科技大学开始承办，目前举行尚不足十届．中国数学会声明：“中国大学生数学竞赛的目的是激励大学生学习数学的兴趣，发现和选拔数学创新人才．”但是中国大学生数学竞赛却分为数学类和非数学类、低年级组和高年级组，这样的做法是否有利于数学人才的发现目前尚不好说，其效果究竟如何还有待时间检验．

6.4 注意数学博士生的性别差异

调查发现，1938—1978年的普特南会员全部都是男性，历史上第一位女性普特南会员是Ioana Dumitriu，时间是在1996年，而1938—2017年一共只有3位女性成为普特南会员，并且迄今为止普特南数学竞赛获奖选手中产生的女性科学家和数学家都非常罕见．这一事实在某种程度上表明，数学能力特别是数学研究能力存在不可忽视的性别差异．因此，数学研究生尤其是博士研究生招生时必须要注意到这种性别差异．数学博士研究生是数学研究主要的后备人才，是未来数学研究的中坚力量．然而，研究者在几所大学调查发现数学院系的女教授、女博导数量很少，但是数学研究生招生时女硕士、女博士并不少，甚至还占多数．这个事实表明，中国数学研究后备人才的培养面临的形势不容乐观，男性数学后备人才的不足将会影响中国数学科学研究的发展．因此，如何吸引更多的男性数学英才加入数学研究队伍应当引起中国数学界和数学教育界的充分重视和思考．

[1] 陈传理，张同君．竞赛数学教程[M]．3版．北京：高等教育出版社，2013：1-2．

[2] 周玲．数学竞赛在中国的实践质问其教育价值[J]．数学教育学报，2010，19（5）：28-30．

[3] 孔企平，张晓玲．从学生数学学习的规律看“奥数”热[J]．全球教育展望，2004，33（5）：70-72，80．

[4] 张维忠．数学“奥赛”：价值、问题与对策[J]．全球教育展望，2004，33（5）：73-76．

[5] 夏兴国．数学竞赛与科学素质[J]．数学教育学报，1996，5（3）：62-64．

[6] 沈文选．奥林匹克数学研究与数学奥林匹克教育[J]．数学教育学报，2002，11（3）：21-25．

[7] 朱华伟．试论数学奥林匹克的教育价值[J]．数学教育学报，2007，16（2）：12-15．

[8] 熊丙章，刘丽颖．论素质教育观下的数学竞赛[J]．数学教育学报，2013，22（6）：66-68．

[9] 贾随军，王尚志，吕世虎，等．中小学生奥数学习的现状调查研究——以“北京市”“兰州市”“重庆市”为例[J]．数学教育学报，2018，27（3）：97-102．

[10]  GALLIAN J. Seventy-five years of the Putnam mathematical competition [J]. American Mathematical Monthly, 2017, 124 (1): 54-59.

[11] 丘成桐，刘克峰，杨乐，等．数学竞赛和数学研究[M]．北京：高等教育出版社，2017：31-44．

[12]  Putnam fellows career paths [EB/OL]. [2018-04-20]. http://www.d.umn.edu/~jgallian/ putnamfel/PF.html.

[13] 李醒民．科学家及其角色特点[J]．山东科技大学学报（社会科学版），2009，11（3）：1-12．

[14]  Mathematics genealogy project [EB/OL]. [2018-04-18]. https://www.genealogy.math.ndsu.nodak.edu/index.php.

[15] 游安军．也论中国数学竞赛的教育性质——与罗增儒先生商榷[J]．数学教育学报，2009，18（1）：48-51．

[16] 张倜，曾静，熊斌．数学英才教育研究述评[J]．数学教育学报，2017，26（3）：39-43．

History and Implication of William Lowell Putnam Mathematics Competition——An Empirical Study

NIU Wei-qiang1, HE Yi-jie2, 3, XIONG Bin2, 3

(1. School of Mathematics and Statistics, Zhengzhou Normal University, Henan Zhengzhou 450044, China;2. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;3. Shanghai Key Laboratory of Pure Mathematics and Mathematical Practice, Shanghai 200241, China)

This article investigated Putnam Fellows’ career paths with secondary data analysis, who are winners of William Lowell Putnam Mathematical Competition in 1938—1978, and analyzed the relationship between Putnam Fellows and scientists, especially mathematicians. It was found that: (1) most (76.4%) of the Putnam Fellows would receive a doctor’s degree especially in science and engineering, and majority of them are in mathematics (including statistics); (2) most (77.0%) of the Putnam Fellows choose scientific research and teaching as their profession; (3) relative majority (60.9%) of the Putnam Fellows would choose to be a mathematician, working in university, college or scientific research institutions for mathematics teaching and research; (4) the gender difference of Putnam Fellows is very significant, no woman has been a Putnam Fellow during the 40 years, and all the mathematicians and scientists in Putnam Fellows are male. These findings have indicated that mathematics competition is an effective method to identify and select talents for mathematics and science research.

Putnam Mathematics Competition; Putnam Fellow; scientist; mathematician

2019-09-16

上海市核心数学与实践重点实验室课题——数学实践（18dz2271000）

牛伟强（1983—），男，河南郑州人，讲师，博士，主要从事数学方法论与数学教育研究．

G421

A

1004-9894（2020）01-0076-05

牛伟强，何忆捷，熊斌．普特南数学竞赛的历史与启示——一项实证研究[J]．数学教育学报，2020，29（1）：76-80．

[责任编校：陈汉君、张楠]