基于HHT方法的地层Q值补偿方法研究
2020-02-28颜中辉徐华宁李攀峰刘鸿杨佳佳陈珊珊杨传胜
颜中辉,徐华宁,李攀峰,刘鸿,杨佳佳,陈珊珊,杨传胜
1. 自然资源部油气资源和环境地质重点实验室,中国地质调查局青岛海洋地质研究所,青岛 266071
2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室,青岛 266071
随着复杂油气藏勘探精度的提高,精细的地震属性反演、油气储层的定量描述都需要高分辨率的地震资料。而地层的吸收衰减作用是影响地震资料分辨率的一个主要因素[1],从而导致了有效反射波频带变窄,相位产生畸变,分辨率和信噪比降低,从而影响了地震资料的成像精度。Q补偿作为一种确定性的处理技术[2],不仅可以补偿地震反射信号的频率和振幅衰减,同时能改善地震子波的相位特性,使中深层的高频部分得到加强,频谱被拓宽,从而有效提高地震资料的质量。
反Q滤波补偿方面也有许多学者进行了研究,基本可以分为3类:用级数展开作近似高频补偿的反Q滤波、基于波场延拓的反Q 滤波和其他反Q滤波方法。最早Hale提出Futterman模型进行反Q滤波的方法[3],该方法基于预测误差滤波分析迭代求出Q值,然后进行Q补偿,其缺点是计算量大。Bickel和Natarajan根据复函数分析技术提出一种反Q滤波方法,此方法基于平面波假设,通过复数对平面波传播进行描述,从而得到时变的Q补偿[4]。Hargreaves和Calvert根据常Q模型得到相位Q补偿方法[5],其做法是通过波场外推来计算常Q模型,从而对相位进行补偿,缺点是未考虑振幅的影响。Bano利用常Q模型发展到层常Q值模型的相位Q补偿方法,优势在于补偿结果能稳定地改善相位的畸变,而且准确性比较高,但同样忽略了振幅的影响[6]。WANG基于等间隔形式的Q模型提出一种稳定有效的反Q滤波方法,此方法以波场延拓理论为基础,并对Q值求取的抗噪性和稳定性进行深入讨论,并不断完善,形成了最常用的反Q滤波算法[7-9]。严红勇和刘洋在WANG方法的基础上,发展成沿射线路径进行波场延拓从而进行Q补偿的方法,主要是针对多分量资料进行处理[10]。刘财等提出基于频率域分时窗吸收补偿的反Q滤波方法[11];Zhang和Ulrych在反Q滤波过程中引入了最小二乘方法和Bayasian原理,从而弥补了Q求取的不稳定性,并在实际数据中得到了很好的效果[12];王本锋等结合反演的思想正则化方法提出了一种新的补偿方法,该方法基于波场延拓的正Q滤波方程,对有效频带内的频率分量进行分析,提高了计算效率,补偿结果稳定高效[13]。叶秋焱利用广义S变换求取时频域表层Q值的方法,通过表层Q值与井控深层Q值建立综合Q体,从而对地震数据进行Q补偿[14]。
虽然地层Q值补偿方法的理论和算法比较成熟,但是在实际地震资料处理应用中一直存在其稳定性和抗噪性不足的问题[15-19],尤其是地层Q值的准确性。本文在HHT方法的基础上,基于EMD自适应分解和HHT时频谱局部刻画能力[20-23],通过将地震资料分成不同的频率段,在HHT时频域计算不同目标层的地层Q值,从而进行Q值补偿。确保了Q值提取精度和Q值补偿的准确性。
1 基于HHT的地层Q值提取
HHT方法的核心内容是固有模态分解(EMD)[24-25],其主要思路是将具有复杂尺度成分的非平稳、非线性信号分解成一组较优Hilbert变换性能的固有模态函数(IMF)之和。我们给定复杂信号X(t),经过EMD自适应分解可表示为:

式中,ci(t)是固有模态函数,rn(t)称为余量。EMD分解其优势在于信号分解过程是自适应的。得到的各个不同尺度IMF都是平稳窄带信号,从而使得波形轮廓对称更好。实际上,EMD方法主要是从频率特征尺度进行分解,第一步得到的是信号中频率特征尺度最小的IMF分量;第二步得到频率特征时间尺度较大的IMF分量;最后分离出来的IMF具有频率特征时间尺度最大的特征。
原信号X(t)分解成多个不同尺度IMF后,基于复数道构建技术,可以构成解析信号Z(t),

Y(t)为X(t)经过Hilbert变换的信号,每一个IMF分量经过Hilbert变换后,构造解析函数可以表示为:
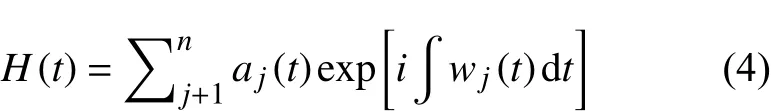
其中,aj(t)为分解的第j阶IMF分量,wj(t)为特定的瞬时频率,对照上式看出,HHT变换实际是傅里叶变换的扩展,优势在于容易反映局部振幅和频率的信息。去除残余函数,展开后得到Hilbert幅值谱,记作:
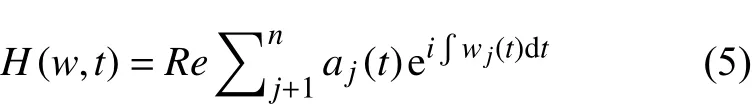
基于HHT分频技术的地层Q值提取方法如下:首先基于HHT时频分析技术对目的层进行分析,选择适合目的层的优势频率范围;然后利用EMD分解技术对地震数据根据频率尺度进行分解,选择只含有目的层优势频率范围的地震数据重构;最后在HHT时频域内通过谱比法计算地层Q值[26]。本文方法在实际地震数据对地层Q补偿应用中的具体步骤为:将实际地震数据分成浅层、中深层,分别对这两套数据进行HHT时频分析,提取局部的频率属性特征,选择适合不同层的频率范围,基于EMD分解技术对这两套数据进行分解、选择、重构处理[27],得到具有不同频率尺度的地震资料;基于复数道技术,在HHT时频域内通过谱比法计算Q值。此做法的优势在于不同频率成分地震信号估算的Q值避免了造成相互影响,同时局部的Q值异常求得更加准确,补偿效果更佳。HHT时频域内谱比法是假定地震子波为零相位子波,其估算地层Q 值的公式为:

式中,τ表示能量衰减率,为一常数,f1表示零相位子波的视频率;f表示平面波频率;t和t1表示平面波从地面开始传播到目的层上下界面所用的时间。W(a,t)表示HHT时频谱。通过公式(6)进行线性回归可以求得地层Q值[28]。
2 地层Q值补偿
地震波在地下传播时,由于信号的中心频率要向较低的频率方向移动,因此找出Q和中心频率的关系至关重要。以此通过Q补偿可以消除地震波在地下介质中传播的频散吸收,提高地震数据的垂向分辨率[29-31]。
在均匀介质中传播的平面波频域表达式为:
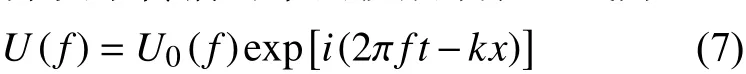
式中,U0(f)表示震源脉冲响应;k为波数;x为波前面沿着射线路径从震源传播到检波器的距离。假如介质是粘弹性,则k为复数,表达式如下:

其中,c(f)为复速度,v(f)为相速度,α(f)为衰减系数。
在Kolsky-Futterman模型中,相速度和衰减系数对应的关系满足:
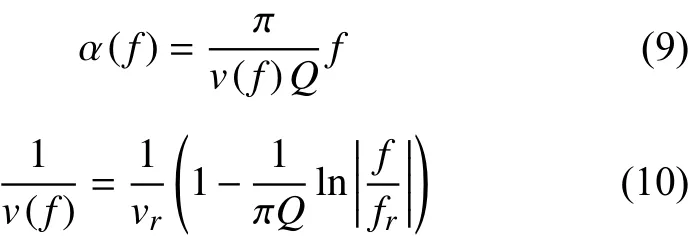
式中,fr代表参考频率;vr代表参考相速度。
于是将公式(8)至公式(10)代入公式(7)中,展开后对应表达式:
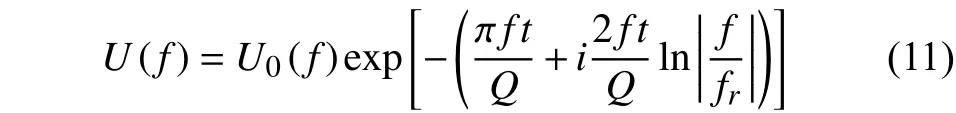

最后进行HHT反变换,得到补偿后的时间域地震信号。
3 模型试验
基于上述理论基础,首先进行模型参数的试验,通过层状介质的衰减模拟分析,以及Q值求取与补偿研究对理论进行验证。模型参数如下:对应层的速度依次为1 500、2 000、3 000 m/s,Q值依次为120、60、120。正演模拟采用基于单程波动方程的分步傅里叶波场延拓方法,采用的地震子波为雷克子波,频率为30 Hz,时间采样间隔1 ms。图1a为模拟得到的地震记录,图2a为放大的波形显示。由于地下介质吸收衰减作用,体现出振幅减小和波形畸变的现象,从放大的波形分析,子波波形不再是零相位,即分辨率逐渐降低。
图3是基于小波分频技术提取的地层Q值曲线,与模型参数基本一致。图1b、图2b是经过本文方法进行补偿后的结果。对比图1a和图2a可以看出,通过Q补偿处理的不同深度地层反射波形均恢复到了原始的雷克子波形态,对应每一层地震信号的振幅和相位都得到了恢复。图4是经过Q补偿前后的振幅谱对比,蓝色为补偿前的频谱,红色为补偿后的频谱。由图可以看出,补偿后的频谱得到展宽。由此可以说明,通过本文方法对地层进行Q值补偿,能够达到使地震子波波形恢复原状,主频提高,频带变宽,提高分辨率的作用。
为了验证本文Q补偿方法的抗噪性,通过对模型数据加入8%的随机噪声,同样的步骤对加噪的数据进行Q补偿测试。图5为补偿前后的数据对比,图6为补偿前后的频谱对比。从图中的对比分析,补偿后的地震记录有效信息得到加强恢复,噪声的部分基本没变。也就是说本文方法在信号补偿的同时,也能确保信噪比。
4 实际数据应用

图1 模型数据Q补偿前后的对比a. 补偿前的地震数据,b. 补偿后的地震数据。Fig.1 Comparison of model seismic data before and after Q compensationa. Model data before compensation,b. Model data after compensation.

图2 模型数据Q补偿前后的波形显示对比a. 补偿前的波形显示,b. 补偿后的波形显示。Fig.2 Waveform comparison of model seismic data before and after Q compensationa. Waveform before compensation,b. Waveform after compensation.
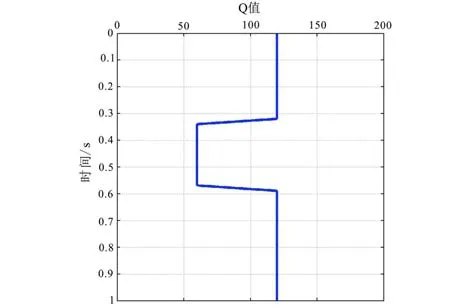
图3 基于HHT方法提取的地层Q值曲线Fig.3 Formation Q-value curve extracted based on HHT method
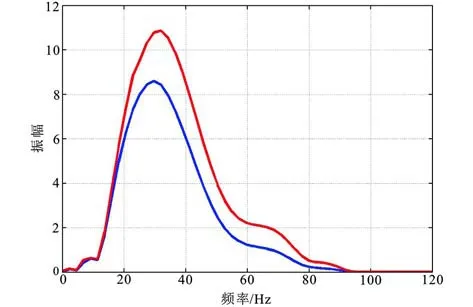
图4 模型数据Q补偿前后的频谱对比Fig.4 Spectrum comparison before and after model data Q compensation

图5 加噪的模型数据Q补偿前后的对比a. 补偿前的地震数据,b. 补偿后的地震数据。Fig.5 Comparison of model seismic data with noise before and after Q compensationa. Model data before compensation,b. Model data after compensation.
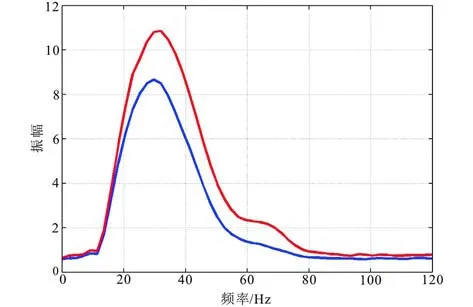
图6 加噪的模型数据Q补偿前后的频谱对比Fig.6 Spectrum comparison of model seismic data with noise before and after Q compensation
本文选择某海域地震资料实际数据对本文方法进行应用效果分析。选取某一段信噪比较好的资料,对其浅层、中深层进行Hilbert分频处理,选择适合不同层的频率区间在HHT时频域计算地层的Q值,进而进行反Q滤波,实现对地层振幅和相位的补偿。图7对应的是根据本文方法求得的Q值剖面,图8a是原始的叠后剖面,从图中可看出Q值剖面跟地层吻合较好。图8b是整个剖面进行补偿后的效果,可以看出分辨率有了显著提高,同时剖面的信噪比也能得到很好的保持。图9为浅层经过补偿后的对比图,补偿后同相轴的连续性有了明显的改善。图10是中深层补偿后的对比图,同样的,补偿后的剖面分辨率更高,地层信息更加丰富。

图7 基于HHT方法提取的地层Q值剖面Fig.7 Formation Q-value profile extracted with HHT method

图8 实际地震数据Q补偿结果对比a. 补偿前的地震数据,b. 补偿后的地震数据。Fig.8 Comparison of actual seismic data before and after Q compensationa. Seismic data before compensation, b. Seismic data after compensation.

图9 浅层数据Q补偿结果对比a. 补偿前的地震数据,b. 补偿后的地震数据。Fig.9 Comparison of shallow data before and after Q compensationa. Seismic data before compensation,b. Seismic data after compensation.

图10 中深层数据Q补偿结果对比a. 补偿前的地震数据,b. 补偿后的地震数据。Fig.10 Comparison of deep data before and after Q compensation resultsa.Seismic data before compensation,b. Seismic data after compensation.
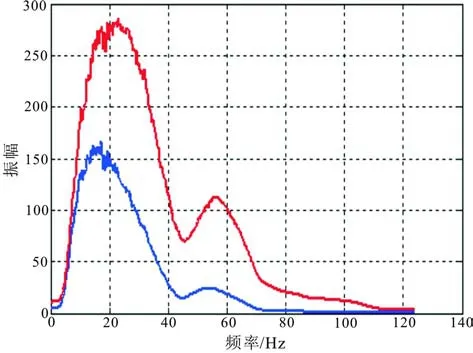
图11 实际数据Q补偿前后频谱对比Fig.11 Spectrum comparison before and after Q compensation

图12 浅层数据Q补偿前后频谱对比Fig.12 Spectrum comparison of shallow data before and after Q compensation
图11 是整个补偿前后振幅谱对比图,图12 为浅层补偿前后频谱对比图。对比可知,Q补偿后的数据频谱有了较大的改善,从浅层到深层表现出高频能量提高,数据主频范围向高频移动,且频谱的形态基本没发生变换,说明补偿是有效的,同时频带变宽,对应的剖面高频成分也有很明显的补偿效果,分辨率有所提高。尤其对中深层的补偿,从图13分析可知,原始资料的高频部信息缺失严重,通过Q补偿后,高频的有效信息被恢复。由于实际数据为海上资料,补偿后高频部分振幅能量得到加强,相应的会导致海上虚反射引起的陷波点效应加剧,海上常规资料处理的方法是通过鬼波压制解决。
为了验证本文方法在提高分辨率的同时,不会损失信噪比,提取噪音部分进行频谱分析,如图14所示,Q补偿后的频谱基本没变换,也就是说噪音的成分没有加强。从补偿的剖面来看,存在信噪比降低的表象,其实只是整个资料主频向高频移动的表现。
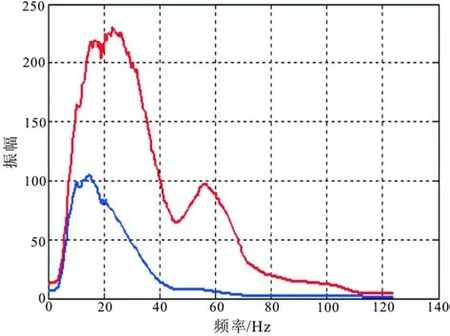
图13 中深层数据 Q补偿前后频谱对比Fig.13 Spectrum compensation before and after Medium-deep data Q-compensation

图14 噪音成分Q补偿前后频谱对比Fig.14 Spectrum comparison before and after noise component Q-compensation
5 结论
(1)HHT变换具有很高的局部分析能力,因此,基于HHT时频谱的地层Q值提取方法能得到更加准确的地层Q值,同时EMD分解算法是基于频率尺度进行分解,可针对不同目标区频率区间进行地震数据的Q补偿,从而达到提高资料分辨率的目的。
(2)通过本文方法进行Q值补偿,在有效提高地震资料主频,展宽频带,提高分辨率的同时,确保了资料的信噪比。从模拟数据到实际地震数据的测试表明本文方法是可行且有效的。
(3)由于EMD分解的过程存在模态混叠效应,同时Q值提取的正确性对资料信噪比有一定的要求。因此,在处理之前应对地震数据进行去噪预处理,以达到更佳的补偿效果。