两相喷射器增压的二级压缩制冷系统性能分析
2020-02-27刘琬琳黄潇治李风雷
刘琬琳, 黄潇治, 李风雷
(太原理工大学 环境科学与工程学院, 山西 太原 030024)
随着科技的进步,人们对建筑舒适性的要求日益增长.在能源日益紧缺的现状下,发展制冷空调节能技术十分重要.Kornhauser[1]提出一种蒸气压缩喷射制冷循环系统,用喷射器代替节流阀回收一部分膨胀功.喷射器是压缩喷射制冷循环中的关键部件.Keenan[2]将喷射器模型分为等压混合模型和等面-积混合模型.Huang等[3]以R141b为制冷剂,建立一维气气等压混合喷射器热力学模型,认为一次流体在喷嘴喉部达到壅塞,并进行验证.朱高强[4]分别计算文献[5-7]提出的3种两相流声速模型,选取与实验结果最为吻合的声速模型,并运用于喷射器的模拟中.Li等[8]建立气液等面积混合两相喷射器的设计模型.王菲等[9]考虑喷射器混合室内产生凝结激波的现象,并提出激波的判断和控制方程.在温度较低的环境中,研究者常采用二级压缩制冷系统降低压缩机的压比,避免压缩机排气温度过高而导致系统运行不稳定.Xu等[10]研究发现,与单级压缩系统相比,二级压缩系统的制冷量和性能系数(COP)都相应地增加10%左右.金旭等[11]研究二级压缩系统的中间压力对系统性能的影响,发现中间压力升高使系统的性能系数出现最优值.基于此,本文提出一种喷射器增压的二级压缩系统(TCRE),并建立喷射器的热力学模型,以R1234yf为制冷剂,采用模拟分析方法对系统性能进行研究.
1 循环原理
两相喷射器增压的二级压缩制冷系统是在传统的二级压缩系统中利用气液分离器进行中间补气增焓,从而达到降低压缩机的压比、扩大系统的运行范围、降低功耗、节能减排的目的.在此基础上,引入喷射器部件,采用喷射器代替节流阀的方法,回收部分膨胀功,大幅减少系统节流过程导致的能量损失,整体提高了二级压缩制冷系统的效率及低压级压缩机的吸气压力,进一步降低压缩机的功耗.
两相喷射器增压的二级压缩制冷系统,如图1所示.图1中:p为压力;h为焓;Δpp1为一次流体入口到喷嘴出口的压力降.由图1(a)可知:来自高压级压缩机的气态制冷剂(状态4)经过冷凝器,冷凝为液态制冷剂(状态5),经过节流阀1,膨胀到与气液分离器1相同的压力(状态6),气液分离器1分离出的饱和液态制冷剂(状态7)为喷射器的一次流体,进入喷嘴;在喷嘴作用下,制冷剂变为高速、低压的气液混合状态,引射来自蒸发器出口的气态制冷剂(状态12),并在喷射器内部进行混合升压,最终形成气液混合物从扩压室出口流出(状态9),进入气液分离器2;气液分离器2分离出的饱和液态制冷剂(状态10)通过节流阀2,变成气液混合物(状态11)回到蒸发器,被一次流体引射进入喷射器,形成喷射器内制冷剂的循环气态制冷剂(状态1)进入低压级压缩机,与来自气液分离器1的饱和汽(状态8)混合,在中间冷却器冷却后(状态3),进入高压级压缩机,增压后进入冷凝器(状态4),完成系统的循环.
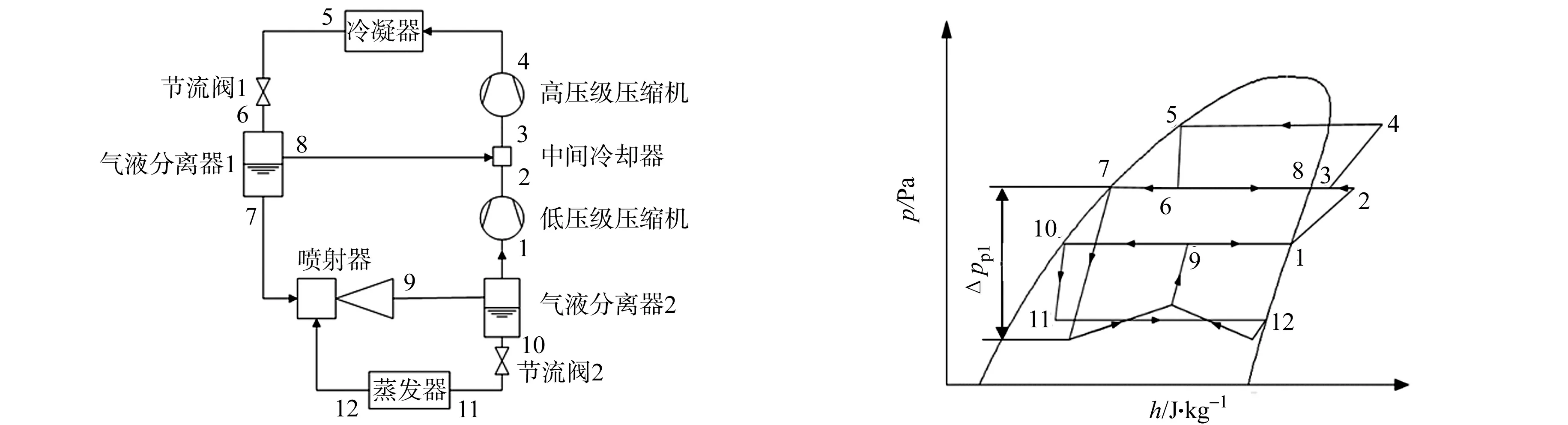
(a) 原理图 (b) 压焓图 图1 两相喷射器增压的二级压缩制冷系统Fig.1 Two-stage compression refrigeration system pressurized with two-phase ejector
2 热力学模型
2.1 喷射器模型
两相喷射器主要包括喷嘴、吸入室、混合室和扩压室4个部分,其结构示意图,如图2所示.图2中:一次流体为液体;二次流体为气体;
2.1.1 基本假设 为简化计算,对喷射器做以下5点假设[12]:1) 在喷射器内,流体的流动为一维稳态流动;2) 一次流体入口、二次流体入口及扩压室出口处的动能忽略不计;3) 在喷射器内,制冷剂的压力损失和热量损失忽略不计;4) 喷射器采用等面积混合模型,一次流体与二次流体在喷嘴出口处达到相同压力,开始混合;5) 喷射器的等熵效率保持不变.
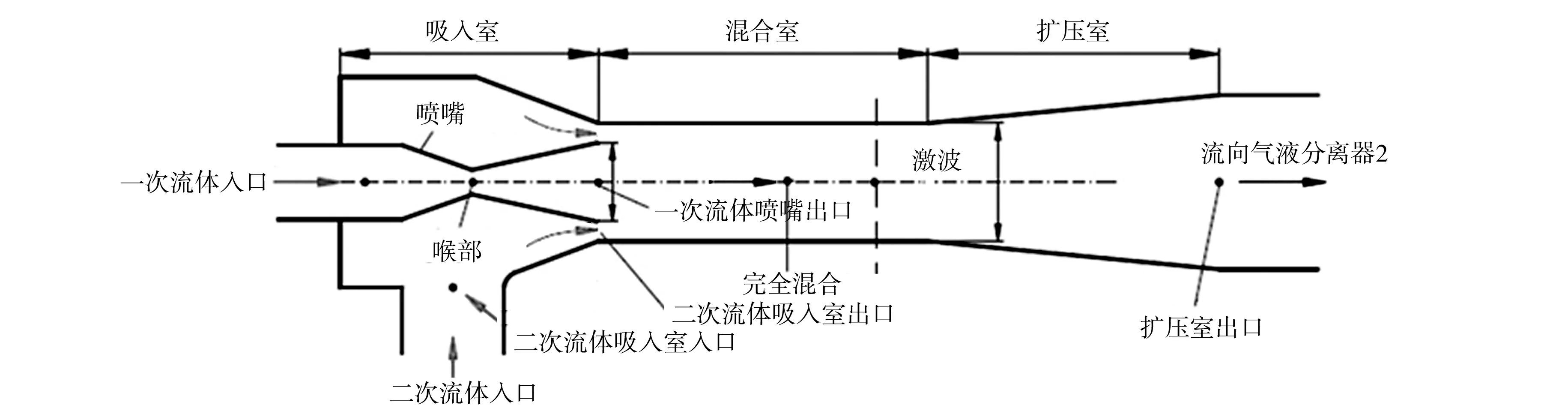
图2 两相喷射器的结构示意图Fig.2 Schematic diagram of two-phase ejector
2.1.2 喷嘴入口到喉部的参数 一次流体从喷嘴入口至喉部的流动过程遵循能量守恒定律,通过喉部的等熵效率ηt考虑流体在实际流动过程中的膨胀损失.喷嘴入口到喉部的参数分别为

(1)
式(1)中:hp0,ht分别为一次流体入口、喉部的焓,J·kg-1;Tp0为喷嘴入口温度,K;ht,s为一次流体从入口到喉部等熵膨胀后的焓,J·kg-1;pp0,pt分别为一次流体的压力和喉部压力,Pa;sp0为一次流体入口的熵,J·(kg·K)-1;vt为喉部流体的速度,m·s-1.
喷嘴将高压的液态制冷剂的压力势能转化成动能,液态制冷剂变成气液混合状态,此时,喷嘴喉部的流体达到壅塞状态,即达到声速[5],有
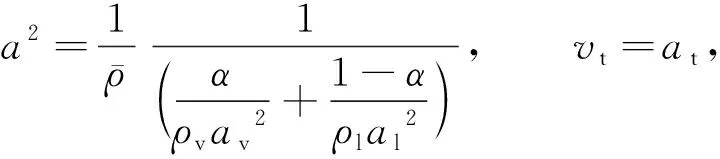
(2)
则喉部面积At为
At=mp/(ρtvt).
(3)
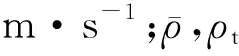
喷射系数ugl是评价喷射器工作性能优劣的重要参数,其计算式为
ugl=ms/mp,mp=m/(1+ugl),ms=mugl/(1+ugl).
(4)
式(4)中:m,ms分别为流过喷射器的流体和二次流体的质量流量.
2.1.3 喷嘴出口参数 流体从喷嘴喉部至喷嘴出口可看作等熵过程,遵循质量守恒和能量守恒定律,可得
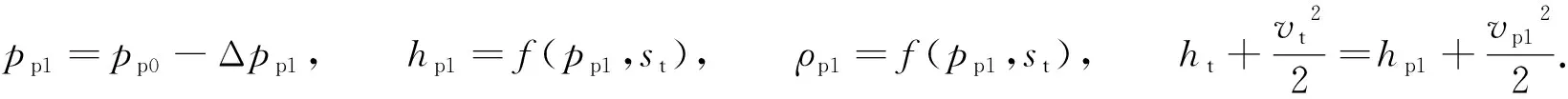
(5)
式(5)中:pp1,hp1,ρp1,vp1分别为一次流体在喷嘴出口的压力、焓、密度和速度;Δpp1为一次流体入口到喷嘴出口的压力降;st为喉部的熵.
喷嘴出口的面积Ap1为
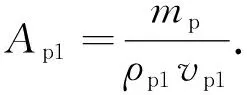
(6)
2.1.4 吸入室参数 已知二次流体入口温度为Ts0,引入吸入室等熵效率ηs=0.98[12],以考虑实际流动过程中的摩擦损失,当一、二次流体到达等面积混合室截面时,压力相等,其流动过程遵循能量守恒定律.二次流体的相关参数分别为
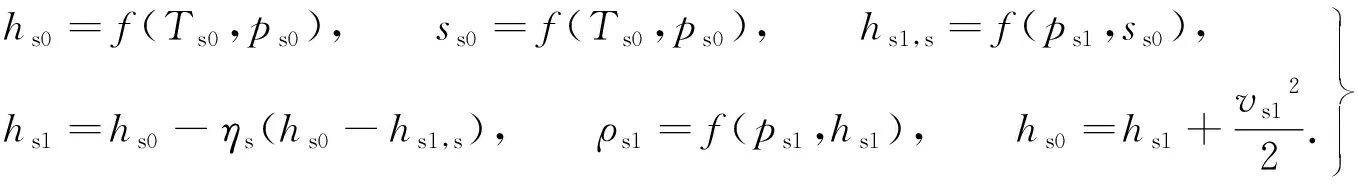
(7)
式(7)中:hs1,s为二次流体从入口到吸入室入口等熵膨胀后的焓;hs0,Ts0,ps0,ss0分别为二次流体入口的焓、温度、压力和熵;hs1,ps1,ρs1,vs1分别为二次流体吸入室出口的焓、压力、密度和速度.
吸入室出口面积As1为
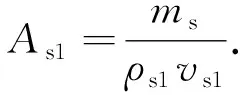
(8)
一、二次流体在喷嘴出口处混合,则等截面混合室面积Am为
Am=Ap1+As1.
(9)
2.1.5 混合室参数 一、二次流体混合后进入混合室,混合流体在混合室内的流动遵循动量、能量、质量守恒定律,可得
pp1Ap1+ps1As1+φm(mpvp1+msvs1)=pmAm+(mp+ms)vm,
(10)
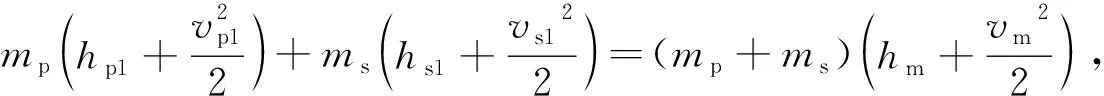
(11)
hm=f(pm,ρm).
(12)
式(10)~(12)中:pm为混合室出口的压力;φm为混合室内两股流体混合造成的动量损失系数;vm,hm,ρm分别为混合室的流体速度、焓和密度.
2.1.6 激波的判断和控制方程[9]如果混合流体完全混合后的速度超过声速,将产生凝结激波.此时,流体压力突增,混合流体的声速am可通过式(2)计算得出.流体的流动过程遵循质量、动量、能量守恒定律,则激波的控制方程为

(13)
式(13)中:ρb,vb,pb,hb为产生激波时的流体密度、速度、压力和焓.
2.1.7 扩压室参数 引入扩压室等熵效率ηd=0.86[13],以考虑混合流体在扩压室压缩过程中的阻力损失.在此过程中,流体速度逐渐减小,压力逐渐升高,动能进一步转化为压力势能,由能量守恒定律可得扩压室出口的相关参数分别为
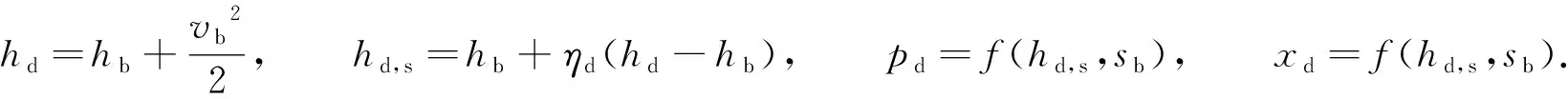
(14)
式(14)中:hd,pd,xd分别为扩压室出口的焓、压力和干度;hd,s为混合流体在扩压室内等熵膨胀后的焓;sb为产生激波时的熵.
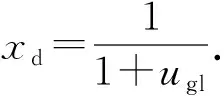
Rlif=pd/ps0.
(15)
2.2 系统其他部件模型
2.2.1 蒸发器参数 蒸发器出口的状态参数为
h12=f(Te,x=1),Qe=ms(h12-h11).
(16)
式(16)中:Te为蒸发温度;Qe为所需制冷量;x为干度;h11,h12分别为状态11,12(图1)的焓.
2.2.2 冷凝器参数 冷凝器出口的参数为
h5=f(Tc,x=0),Qc=(mp+ms)(h4-h5).
(17)
式(17)中:Tc为冷凝温度;Qc为换热量;h4,h5分别为状态4,5(图1)的焓.
2.2.3 节流阀参数 给定中间温度Tn,可计算出节流阀1的出口参数T6=Tn,h6=h5,p6=f(T6,h6),x6=f(T6,h6);节流阀2的出口参数h11=h10.
2.2.4 气液分离器参数 气液分离器将气液两相制冷剂分离为饱和汽态制冷剂和饱和液态制冷剂,气液分离器1的出口参数h8=f(p6,x=1),h7=f(p6,x=0),状态8,7分别为气液分离器分离出的饱和汽和饱和液.同理,气液分离器2的出口参数h1=f(p9,x=1),h10=f(p9,x=0),状态1,10分别为气液分离器分离出的饱和汽和饱和液.
2.2.6 中间混合的参数 进入高压级压缩机的流体的质量流量mr2为流经低压级压缩机的流量与来自气液分离器1的饱和汽质量流量之和,混合后使来自低压级压缩机的排气温度冷却至与中间冷却器相同的温度,根据热平衡,有mr1h2+mr2h8=(mr1+mr2)h3.
2.3 系统性能计算模型
系统的性能系数COP、系统相对于传统二级压缩系统的性能系数提高率δCOP,以及系统总功率Pcom分别为
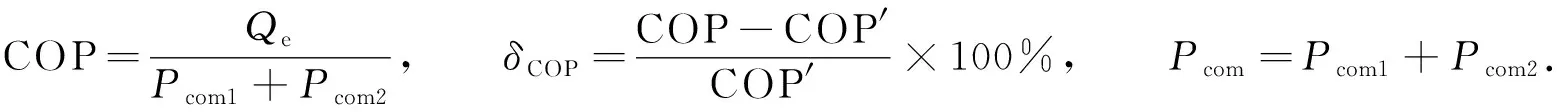
(18)
式(18)中:COP′为传统二级压缩系统(TCRS)的性能系数[15].
3 结果与分析
3.1 中间温度对系统性能的影响
在二级压缩系统中,中间压力对系统性能具有明显的影响.制冷系数最大时的中间压力为最优中间压力,其对应的温度为最优中间温度.为方便叙述,蒸发温度、冷凝温度、中间温度均采用摄氏温度.
当蒸发温度te为0 ℃,冷凝温度tc分别为45,50,55 ℃时,中间温度tn对喷射器增压的二级压缩系统性能系数的影响,如图3所示.由图3可知:随着中间温度的升高,COP先增大后减小;存在最优中间温度,分别为25,30,35 ℃.这是因为随着中间温度的升高,开始时,喷射器一次流体入口的压力变大,喷射器升压比变大,使压缩机的压比减小,压缩机功率减小,系统性能提高;随着中间温度继续升高,喷射器升压比增长缓慢,低压级压缩机的压比持续增加,功率增大,系统性能系数下降.
当蒸发温度为0 ℃,冷凝温度为50 ℃时,系统的COP,COP′,δCOP随着中间温度的变化情况,如图4所示.由图4可知:当中间温度从15 ℃升高到40 ℃时,COP,COP′先增大后减小;COP从3.70增加到4.11,又减小到3.97,最优中间温度为30 ℃;COP′从3.57增加到3.79,又减小到3.39,最优中间温度为25 ℃;COP′减小的程度比COP大,COP始终大于COP′;δCOP从3.64%升高到17.10%.这是因为随着中间温度的升高,TCRE和TCRS系统的低压级压缩机的压比都持续增加,但TCRE系统中的喷射器也具有增压作用,因此,低压级压缩机升压比增大的程度小于TCRS系统,压缩机功率较小,系统的性能系数提高率变大.由此可见,喷射器增压的二级压缩系统的经济性更优.
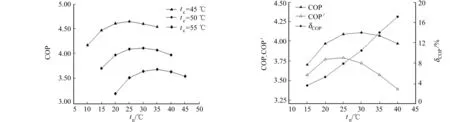
图3 不同冷凝温度下COP随着中间温度的变化情况 图4 COP,COP′,δCOP随着中间温度的变化情况Fig.3 Variation of COP with intermediate temperature Fig.4 Variation of COP, COP′and δCOP at different condensation tempetatures with intermediate temperature
3.2 蒸发温度对系统性能的影响
当冷凝温度为50 ℃时,COP,喷射系数ugl和喷射器升压比Rlif随着蒸发温度的变化情况,如图5所示.由图5可知:当蒸发温度从-15℃升高到10 ℃时,COP从2.85升高到5.43,喷射系数从0.71升高到0.82,升压比从1.12下降到1.04.这是因为随着蒸发温度的升高,喷射器入口的二次流体的温度升高,二次流体的压力与流量增大.因此,喷射系数增加,升压比减小,蒸发器的制冷量变大,COP也变大.
当冷凝温度为50 ℃时,COP,COP′,δCOP随着蒸发温度的变化情况,如图6所示.由图6可知:随着蒸发温度从-15 ℃升高到10 ℃,COP,COP′逐渐增大,且COP始终大于COP′,而δCOP从9.46%下降到7.31%.这是因为当冷凝温度一定时,蒸发温度越高,两者温差越小,喷射器回收的膨胀功越小,δCOP就越小.

图5 COP,喷射系数,升压比随着蒸发温度的变化情况 图6 COP,COP′,δCOP随着蒸发温度的变化情况 Fig.5 Variation of COP, entrainment ratio and Fig.6 Variation of COP, COP′ and pressure lift ratio with evaporating temperature δCOP with evaporating temperature
3.3 冷凝温度对系统性能的影响
当蒸发温度为0 ℃时,COP,喷射系数ugl及喷射器升压比Rlif随着冷凝温度的变化情况,如图7所示.由图7可知:当冷凝温度从35 ℃升高到60 ℃时,系统COP从6.14下降到3.26,喷射系数从0.85下降到0.69,升压比从1.03升高到1.13.这是因为随着冷凝温度的增加,一次流体的动能与质量流量也增加,喷射系数减小,一次流体入口压力变大,升压比随之变大,由于冷凝器与蒸发器的压差增大,压缩机压比变大,功率增加,所以系统性能系数减小.
当蒸发温度为0 ℃时,COP,COP′,δCOP随着冷凝温度的变化情况,如图8所示.由图 8可知:当冷凝温度从35 ℃升高到60 ℃时,COP与COP′都逐渐减小,COP′减小的程度比COP大,δCOP从3.02%升高到10.63%.这是因为当蒸发温度一定时,随着冷凝温度的升高,喷射器升压比变大,压缩机的功率减小,相较于传统的二级压缩系统,TCRE系统性能系数的优势更为明显.

图7 COP,喷射系数,升压比随着冷凝温度的变化情况 图8 COP,COP′,δCOP随着冷凝温度的变化情况Fig.7 Variation of COP, entrainment ratio and Fig.8 Variation of COP, COP′ and pressure lift ratio with condensation temperature δCOP with condensation temperature
4 结论
提出喷射器增压的二级压缩制冷系统,建立系统热力学模型,分析中间温度、蒸发温度和冷凝温度对系统性能的影响,以及相对于传统二级压缩系统性能系数的提高率,得出以下3点结论.
1) 当蒸发温度升高时,系统COP和喷射系数均增大,喷射器升压比减小;当冷凝温度升高时,系统COP和喷射系数均减小,喷射器升压比增大.
2) 当冷凝温度为50 ℃,蒸发温度为0 ℃,中间温度为15~45 ℃时,系统COP先增大后减小,最优中间温度为30 ℃.
3) 当冷凝温度为35~60 ℃,蒸发温度为-15~10 ℃时,喷射器增压的二级压缩系统性能始终优于传统二级压缩系统.当冷凝温度与蒸发温度的温差较大时,采用喷射器增压的二级压缩系统的性能提升作用更为明显,提高率最高可达10.63%.
