复杂沉积区地震剖面时深转换的多公式拟合方案及应用
2020-02-27汪俊徐子英任卫波
汪俊,徐子英,任卫波
(1.广州海洋地质调查局,广东 广州 510760;2.自然资源部 海底矿产资源重点实验室,广东 广州 510760;3.广东地下管网工程勘测公司,广东 广州 510075)
0 引言
地震剖面解释多基于时间域剖面,而最终成果(如沉积厚度图、地层结构图和地质剖面图等)须以深度域数据展示,其间涉及地震资料的时深转换。速度数据主要来源包括:钻孔速度资料和地震速度谱分析获取的速度资料。
钻孔经济成本高昂,即使在勘探程度高的含油气盆地亦分布稀少,不足以精细描述勘探区三维空间内的速度分布规律;联合钻孔速度和地震速度数据获取勘探区较高精度的速度资料成为油气勘探的常见方法[1-10]。海洋区域地震勘探覆盖范围广,在无钻井速度资料可用的情况下,利用地震速度资料开展时深转换工作成为唯一选择。
由速度谱分析方法获取的速度资料优点与缺点并存,其缺点是分辨率相对较低,可靠性相对较差,尤其是在复杂构造区域[2,8-9]和海盆深水区域[11],其优点是可以沿地震剖面密集地获取速度资料,藉此不仅可以了解速度的纵向变化规律,还能分析速度的横向分布特征。
与小区域高调查程度的油气勘探不同,海洋区域地质调查一般无钻井速度资料,二维地震测线网度相对稀疏(如1∶100万比例尺的测线网度为20 km×40 km),勘探面积较大,无法像油田三维地震勘探一般形成高精度的地震速度体[2-10,12]。因此,海洋区域地震勘探时深转换工作一般利用沿地震剖面获取的速度谱资料,拟合一个适用于整条剖面甚至全区的折中时深转换公式[13],或者计算各个层位的地层速度,逐层进行时深转换[14],即“常速度剥层法”。此两种方法忽略了地层厚度变化以及岩性异常等地质因素引起的速度横向变化[15-17]。为考虑地层速度横向变化,此前笔者基于沉积层“速度—深度”线性模型建立了针对深海盆沉积的时深转换方案[18],但该方案在理论上仅考虑沉积地层的压实作用,仅适用于沉积环境稳定、地层厚度较薄的区域。当“速度—深度”线性模型无法满足精细时深工作需求时,不得不寻求更加合适的时深转换方案。
1 “时间—层速度”拟合公式选择
当沉积地层厚度达到一定程度时,速度随深度的增长率减小(图1a),若转换成速度随时间的变化关系,即在试验地震剖面 “时间—层速度”散点图(图1b)中,双程走时0~3 s范围内层速度随时间的变化趋势亦符合指数增长规律,双程走时超过3 s以后,层速度增长率锐减。因此笔者考察了指数公式(式1)、幂函数(式2)和二次多项式(式3)3种拟合公式的数学性质[19-20](图2)。
V(t)=v0etβv0,
(1)
V(t)=atb+v0,
(2)
V(t)=at2+bt+v0。
(3)
式中:V是层速度;v0是初始速度;t是双程走时;β是“速度—深度”线性模型中的速度增长系数;a和b是幂函数和二次多项式的两个拟合参数。
指数公式(式1)是基于沉积层“速度—深度”线性模型[11,18],该模型表明沉积地层的层速度随时间呈指数增长(图2a),显然无法适应试验地震剖面“时间—层速度”散点图(图1a)中显示的随时间增长,层速度增长率衰减的情形。
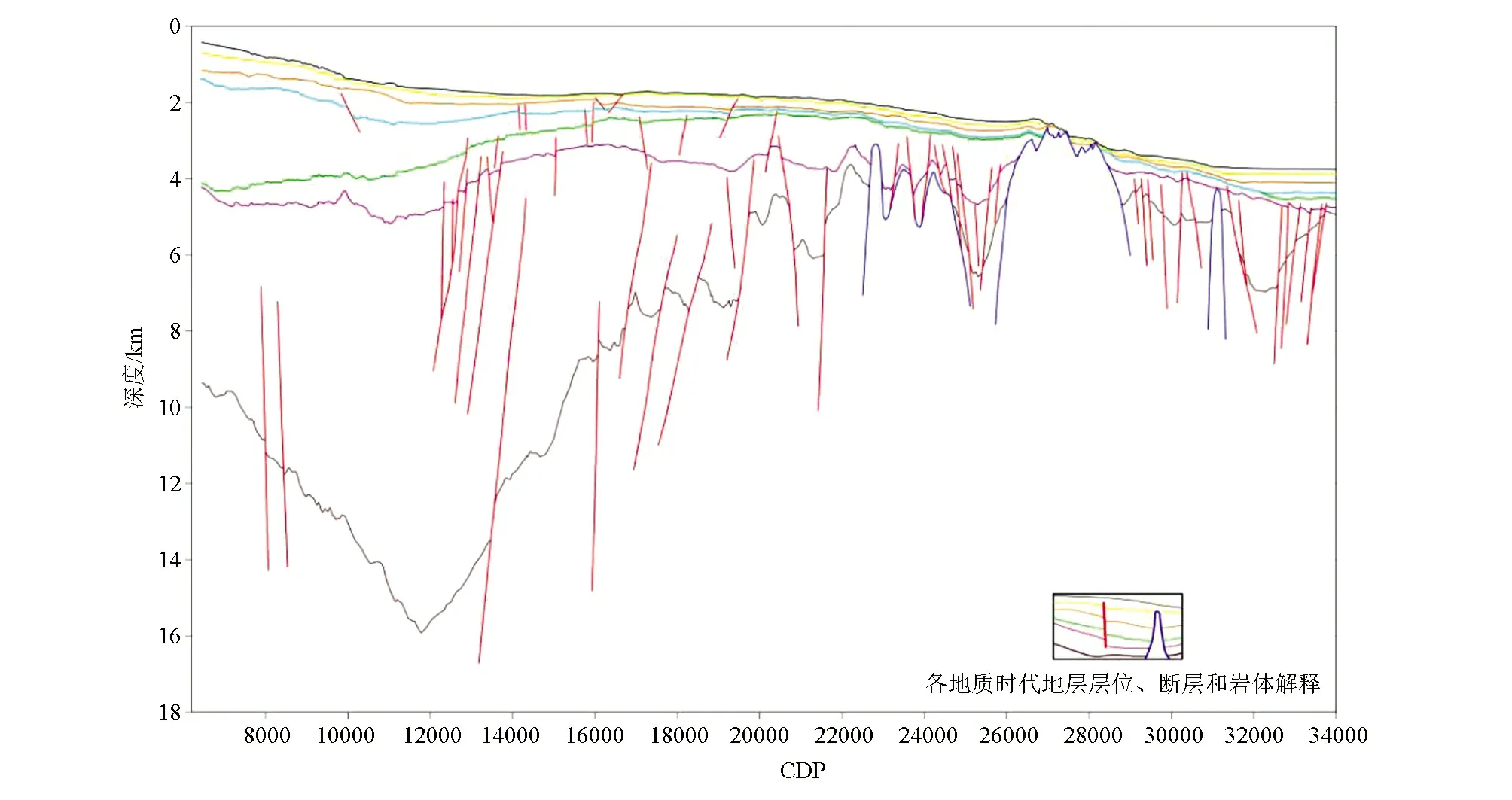
在幂函数(式2)中,当拟合参数0 在二次多项式(式3)中,当拟合参数a>0,且b>0时,该函数可适应“时间—层速度”的指数增长情形(图2c);当拟合参数a<0,且b>0时,该函数可适应“时间—层速度” 关系中层速度增长率衰减的情形(图2d)。不过应注意,在第一种情形中,当t>b/(2a)时,速度会随时间减小,即出现所谓的“速度反转”,显然不符合沉积地层速度的变化规律。 将3种公式应用于试验地震剖面上各种沉积类型的“时间—层速度” 关系拟合中,以检验其适用性,并对比各拟合公式的适用程度(图3)。CDP8421、CDP11781和CDP15781位置的“时间—层速度”剖面代表巨厚沉积区地层厚度变化的情形,CDP21381、CDP25221和CDP32261则代表沉积凹陷边缘隆起和局部凹陷地层厚度变化的情形。在评估拟合结果时引入“拟合优度”的概念[19],即相关系数的平方(式4),拟合优度大于0且小于1,越接近1表示拟合程度越高: (4) 图1 试验地震剖面“深度—层速度”(a)和“时间—层速度”(b)散点图 对比结果(图3)表明,在巨厚沉积区(CDP8421、CDP11781和CDP15781),指数公式的拟合优度(<0.85)明显劣于幂函数和二次多项式(>0.94),幂函数和二次多项式的拟合优度相近,二次多项式拟合程度略优于幂函数;在沉积凹陷边缘隆起和局部凹陷区域(CDP21381、CDP25221和CDP32261),幂函数和二次多项式的拟合优度相近,大都在0.9以上,指数公式、和幂函数拟合优度逐次增大。 由此可见,二次多项式在巨厚沉积区的“时间—层速度”关系拟合中的适用度最高,幂函数在试验地震剖面其它区域“时间—层速度”关系拟合中表现最好,而指数公式在试验地震剖面任何区域“时间—层速度”关系拟合中表现最差。 因此,笔者尝试根据拟合优度大小,在试验地震剖面不同区域分别应用不同的拟合公式,以寻求整体拟合程度最优的时深转换方案。 试验地震剖面位于南海北部陆缘某海域,涵盖了盆地巨厚沉积区(沉积地层厚度对应的双程走时普遍在3 s以上,最厚处达6 s以上)和沉积环境变化较大的陆—洋转换区域(图3),沉积环境的变化较为复杂,是验证多公式拟合时深转换方案有效性的理想区域。 沿试验地震剖面拾取均方根速度的谱点间距为1 km,最终拾取共计173个均方根速度谱点(图4)。应用DIX公式[21](式5),将每个谱点的均方根速度换算成层速度。 (5) 式中,Vr,i为底界均方根速度;Vr,i-1为顶界均方根速度;t0,i为底界反射时间;t0,i-1为顶界反射时间。 图4 沿地震剖面的层速度及拟合参数分布 对173个“时间—层速度”剖面分别用指数公式、幂函数和二次多项式进行拟合,以拟合优度为依据在试验地震剖面不同区域分别应用不同的拟合公式,以寻求整体拟合程度最优的时深转换方案。 拟合结果表明(图4),在试验地震剖面的厚沉积区(CDP6501~21060),二次多项拟合优度与幂函数拟合优度均在0.9以上,明显优于指数公式拟合优度(多在0.7~0.9之间),而二次多项拟合优度略优于幂函数拟合优度,因此该区段的“时间—层速度”关系采用二次多项拟合方案;在试验地震剖面的沉积凹陷边缘隆起区及陆坡—深海盆转换区(CDP21061~30661),二次多项拟合优度与幂函数拟合优度相当(在0.8~0.9之间),明显优于指数公式拟合优度(大多在0.6~0.8之间),而幂函数拟合优度略优于二次多项拟合优度;在深海盆区(CDP30661~34000),式3中的拟合优度差别不大,拟合优度在0.65~0.9之间,而幂函数拟合优度相对最优。因此,后两段区域(CDP21061~34000)的“时间—层速度”关系采用幂函数拟合方案。 另外,将拟合优度明显低于相邻区域的CDP点位视为异常“时间—层速度”剖面,给予剔除(本次试验剔除了31个异常“时间—层速度”剖面),采用相邻区域拟合曲线的折中曲线(技术上采用拟合参数线性插值),以保证速度场平缓连续变化(图4)。 Z(t)=a/(b+1)t(b+1)+v0t, (6) Z(t)=(a/3)t3+ (b/2)t2+v0t。 (7) 式中,Z是深度(从海底起算);v0是初始速度;t是时间;a和b是幂函数和二次多项式的两个拟合参数。 经计算得出的深度域地震解释资料(图5)显示,各地层界面基本保持了时间域剖面的形态。因速度随时间增长,沉积厚度随时间加速增厚,厚沉积区的沉积厚度在3~15 km之间,相比剖面其余区域几百米至3 km的沉积厚度,横向差异比时间域剖面更显著。 图5 地震解释资料的深度域剖面 引入拟合优度概念,在地震剖面不同区段采用相对适用的“时间—层速度”拟合公式,即“多公式拟合方案”。该方案是针对复杂沉积区地层时深转换工作的一种尝试,其优点是兼顾了沉积地层速度的横向变化和地层压实作用之外的影响。 考虑到海洋区域地震勘探覆盖范围广,涉及构造环境更为特殊的区域[1-2,6-7,10,16,22],如:陆坡崎岖海底区[22]、复杂断块构造区[1-2]和速度反转区[10]。对于特殊构造区的时深转换工作,采用笔者的方案会造成较大误差,还需采用针对性的方法,如在速度体建模时加入断层格架及层位等地质模型的约束[2,4,15]。 归根结底,时深转换工作最本质的部分是可靠速度模型的建立,从人工地震资料处理原理出发,从根本上改进速度模型的可靠性是最核心的也是难度最大的研究方向。由叠前深度偏移处理方法获取的速度模型目前被认为最可靠,不过其处理效率低成本高,并非性价比最高的手段。由叠前时间偏移等性价比较高的手段获取的速度资料出发,通过公式拟合、地质模型约束等手段提高速度模型可靠性是一个务实的研究方向。 引入拟合优度概念,在地震剖面不同区段采用相对适用的“时间—层速度”拟合公式,建立了沉积地层时深转换工作的多公式拟合方案,结论如下: 1)相比基于“速度—深度”线性模型的指数公式,沉积地层多公式拟合方案适用范围更广,可应对不同构造环境沉积地层时深转换工作; 2)“多公式拟合方案”实践表明,在厚沉积区,二次多项次拟合的适用性最佳,在构造活动区幂函数拟合的适用性最好。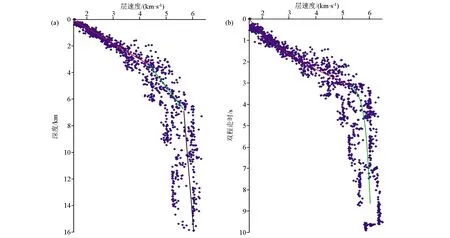
2 多公式拟合时深转换方案的应用
2.1 均方根速度拾取与层速度计算
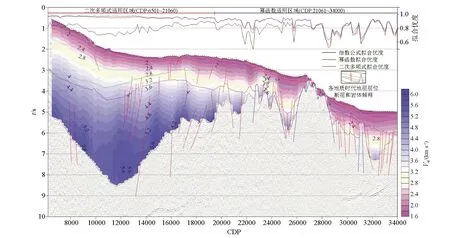
2.2 多公式拟合方案的确定
2.3 时深转换
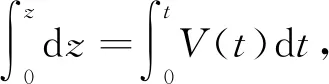
3 讨论
4 结论
