基于叠前反演的地应力预测方法应用

王超，宋维琪，林彧涵，张云银，高秋菊，魏欣伟

(1.中国石油大学(华东) 地球科学与技术学院，山东 青岛 266580；2.中国石化胜利油田分公司物探研究院，山东 东营 257000)

0 引言

随着油气资源更深层次的勘探开发，勘探目标逐渐转向非常规低渗透油气藏，目前中国探明的石油地质储量中，低渗透储量占了很高的比例，致密砂岩层将是我国今后相当长一段时期油气增储上产的主要目标，因而对于深层地应力分布与规律表征的研究逐渐变得非常有意义。地应力的概念最先是由瑞士学者Heim提出来的，所谓地应力是指存在于地层中未受工程扰动的天然应力，并假设原岩应力在各个方向上均相等，即静水应力状态。有其他学者统计了世界各地区的应力分布情况，总结了垂向应力分布规律[1,2]。经过统计分析，认为地应力随泊松比的增大而减小[3]。而后统计实测地应力与杨氏模量的关系，发现水平最大主应力和水平最小主应力与杨氏模量成正相关[4]，但是以上研究都未能指出应力的定量关系。同时出现了基于地震数据估算地应力的方法，利用该方法估算水平应力差异比，即最大和最小水平应力差与最大水平应力的比值，它是指示地层中水平两个方向应力差异大小的指示因子[5,6]。对于弹性参数的反演，国内学者推导出基于Ruger反射系数的各向异性弹性阻抗公式[7]。国外学者提出了各向异性弹性阻抗的概念，并分析了各向异性弹性阻抗与各向同性弹性阻抗的差异[8]，但其方程及阐述过于复杂，不便于分析各向异性对弹性阻抗的影响。在叠前反演出弹性参数后推导了正交各向异性介质的地应力计算公式，同时提出了正交各向异性水平应力差异比ODHSR的概念[9]，但是尚未在砂泥岩中应用。

研究主要以砂泥兼互层为研究目标，结合叠前地震资料和已有构造解释结果，探究了适合目标层的地应力大小预测方法。首先，利用各向异性阻抗方程进行推导，利用叠前反演的方法得出了地层弹性参数及裂缝弱度参数，进而转化为各向异性参数；其次，运用已有的地质资料，得到了曲率和曲率计算下的应力分布与基于井点模型下计算的地应力；最后，在基于正交各向异性模型假设下计算出了差应力之比，与其他几种应力表征结果对比，检验砂泥岩地应力大小预测方法的准确度和合理性。研究结果表明，曲率预测的结果同正交介质模型假设下计算出的地应力预测结果基本一致，垂向上的大小趋势与测井资料吻合，证明了文中提出的地应力大小预测方法在砂泥岩层中适用，与传统计算方法相比更加突出了水平方向的应力分布，在对于未来低渗透油气藏的勘探开发有良好的指导作用。

1 各向异性弹性阻抗反演

(1)

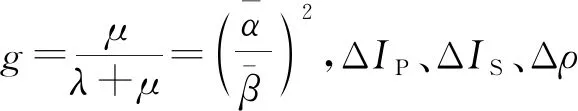
通过分析可以看出式(1)中的密度项对于整体的反射系数数值影响很小，并且直接通过反演得到的密度并不十分准确，因此为了简化计算可以先略去密度项[13]，在后续的计算中间接得到密度，所以反射公式可以简化为：

以上为各向同性部分的公式变换，再对各向异性弹性阻抗扰动项进行分析，扰动项反射系数可以表示为[15]：

g(cos2φsin2θ)RΔT，

(4)

式中RΔT为切向弱度，RΔN为法向弱度(后面用ΔT、ΔN表示)。弱度参数对于裂缝的指示有重要意义，可以将不同方向的资料进行差值求取，更容易获得准确的弱度参数。将式(4)代入式(3)可得：

2g(cos2φsin2θ)RΔT-2(gcos2φsin2θ)(1-2g)RΔN。

(5)

在假设地下介质具有连续性的基础上对式(5)两边积分并进行指数化，为了能够从弹性阻抗数据体中反演出稳定的弹性参数，需要对方程进行线性化处理，即：

c(θ,φ)ΔT+d(θ,φ)ΔN

(6)

式中a(θ)=sec2(θ),b(θ)=-8gsin2θ,c(θ,φ)=2gcos2φsin2θ,d(θ,φ)=-2(gcos2φsin2θ)(1-2g)。

从式(6)可以看出，如果想通过方位各向异性弹性阻抗计算出纵横波弹性阻抗以及扰动系数，至少需要4个不同方位角、入射角的地震道集，不同入射角方位角的弹性阻抗对数方程组为：

(7)

为了求解IP、IS、ΔT、ΔN，将式(7)简化为d=Gm，结合已知的地质和测井信息，将其加入可作为先验信息，运用基于模型先验约束的阻尼最小二乘法反演方法进行求解[16]，即：

m=dmod+[GTG+μI]-1GT(d-Gdmod)

(8)

I为单位矩阵。

2 各向异性参数转化

从上述方程可以看出，阻抗项随着入射角和方位角的变化而变化，因此可以利用分方位角道集来反演地层的裂缝弱度信息及弹性参数。在反演过程中，特别是对于叠前地震资料，资料的品质直接影响着反演的精度。前期对于资料的工作主要有叠前资料的去噪及补偿、角道集的的选取、测井资料处理、地震子波的选取、叠前弹性阻抗反演等。在将炮检距数据转化为角道集的过程中，应该在前期地质分析资料的基础上根据裂缝走向来划分角道集，这样可以更好地突出各向异性信息，在所有的关于裂缝的检测分析之前，都必须采用与方位有关的几何扩散和垂直入射包络归一化这两个处理流程，如果横向非均匀性很严重，就需要对方位角道集进行偏移，然后叠加，这样可以有效地提高反演结果的品质。利用角度子波、测井资料、地震数据可以建立低频模型来进行阻抗反演，可以得到不同入射角和方位角的弹性阻抗数据体。然后利用上述的方法进行下一步计算，即可求出需要的参数(图1)。

与常规地层相比，在计算砂泥岩各向异性参数前需要对反演的结果加以处理，主要采用区域性提频和均值化处理，减少反演中因地层横向变化较快而导致的速度突变，在计算应力时容易引起局部突变，如图2所示，提升了计算的稳定性。

图1 应力预测流程

图2 反演结果进行处理

利用已经求出的裂缝弱度参数，根据裂缝弱度与各向异性参数之间的关系[17]：

(9)

式中,δ(v)、ε(v)和γ(v)为各向异性参数。利用求得的波阻抗可以间接求出纵横波速度以及密度信息，作为该地区的背景数据，由于地下地质情况复杂，在精度要求不是很高的情况下，可以近似看作真实的地质参数。

利用HTI介质与VTI介质的各向异性参数转化关系[18]，即

(10)

可以得到VTI介质下的各向异性参数γ，用于计算正交各向异性介质的地应力。

3 地应力大小计算

对于地应力计算的研究目前还是比较有限，当前油田中较常用的是通过建立井点模型来预测地应力的分布，这种方法对于测井数据的依赖程度很大。从地震数据方面来预测地应力分布变得更有意义，因而，Gray提出了DHSR水平应力差异比这个概念，利用地震数据可以直接估算地层中的水平主应力[6]，该方法的优点是减少了地应力计算中对井数据的需求，可以通过少量井数据来计算出目标工区的地应力。为了包含VTI特征的存在，马妮考虑了各向异性垂向与水平对称轴的作用[9]，推导了正交各向异性介质下，通过地震数据计算水平应力差异比的公式，即正交各向异性水平应力差异比(ODHSR)公式。文章基于叠前反演得到了地下介质弹性参数，并且求取了VTI介质下的各向异性参数，并假设所求取的VS即为极化方向为x方向的准横波垂向速度VS0，VP即为准纵波的垂向速度VP0，最终利用测井数据来检测假设的合理性。利用最大水平地应力σy和最小水平地应力σx可以得到正交各向异性水平应力差异比(ODHSR)近似公式：

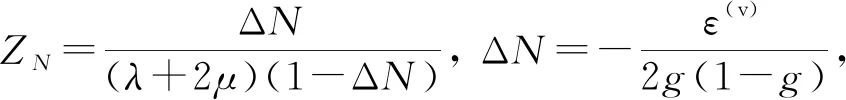
λ和μ为拉梅参数，ΔN为裂缝法向弱度。分析公式可知，ODHSR的值越低表明该区域的最小水平应力和最大水平应力的大小数值越接近，相反数值较大地区可解释为构造运动区域，极有可能是断裂所产生，因而可以通过与该地区的断裂解释图进行对比，进而判断出应力场计算的合理性。

4 实际资料分析

所选实际资料为中国某勘探区域，该区域为中新生代的断陷盆地，裂缝发育较多，研究的目的层为致密砂岩层，层内包含泥质体，为砂泥兼互层。由于埋深较大，储层物性变化快，砂泥组合复杂，常规预测方法难以奏效，需要进行提频处理，区域均值化。如何正确的识别出应力的分布情况，正在困扰着油田当前的勘探开发工作。现有计算地应力分布的方法多基于测井开发所得数据而来，存在诸多限制。该研究计算了多种预测方法来表征该工区的地应力分布特征，从不同的表征角度出发，计算出了多种结果，相互对比，增强了预测准确度和可靠性。选用的地震资料为叠前全方位地震数据，根据需要对地震资料进行前期的处理来满足计算的需要。然后利用笔者所提的叠前反演，得到弹性阻抗和裂缝柔度系数，进而求解出纵横波速度、密度，再通过裂缝弱度与各向异性参数之间的关系给出的[17]，获得了各向异性参数，以求得的数据结果作为实际工区的背景数据(图3)，忽略反演模型的影响，作为正交各向异性模型的参数数据。

曲率是一种从构造角度出发得到的参数，用来表示地层弯曲程度，当构造曲面的曲率增加时，应力也随之变化。笔者计算出了倾角曲率数据，并参考了将曲率与杨氏模量的乘积近似表示为地层应力曲率的理论[19]，从曲率的角度计算了地应力，得到了地应力的分布状况(图4)，可以作为一种应力计算的参照量。

传统的应力计算方式一般是基于井点模型而做出的，这种计算方法对于井数据要求很大，需要大量的井数据，存在很多不便。在本地区通过井点模型计算的应力如下(图5)，可以看出应力的分布成阶梯状，通过分析得知，由于目的层存在倾角，因而应力计算受重力影响较大，而我们通常需要的是水平应力，所以这种计算方式存在着很大的缺陷，不能对水平应力分布进行客观的表征。

a—vp;b—vs;c—ρ;d—ε(v);e—δ(v);f—γ(v)

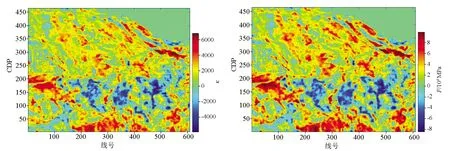
图4 曲率(左图)和曲率计算的应力(右图)表征的层位切片

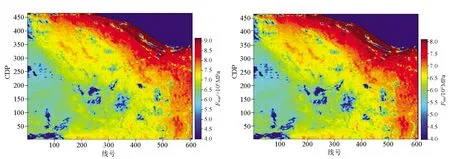
图5 最大地应力(左图)和最小地应力(右图)的层位切片

利用叠前反演得到弹性参数和各向异性参数，通过对ODHSR公式计算参数的假设，利用正交各向异性水平应力差异比公式，计算出差应力之比，并与测井曲线进行了对比。选取本工区内的A井，根据计算的最大最小主应力，进行了差应力之比的计算，由于计算方式不同，采用了归一化的方法，将两者放置于同一数量级，可以看出整体趋势吻合(图6)。

图7为某油田对于该地区目的层的断层解释图(将解释的断层数据绘制到层位中)，大型断裂十分清楚，但是由于解释不够精细，小型断裂并未刻画出来。断层、裂缝和地应力有着密切的关系，通常裂缝的产生就伴随着应力的释放，因而可以认为裂缝是应力在宏观上的表现，运用裂缝能够表征应力分布，同样应力的分布也能解释裂缝的存在。利用文中的预测方法计算出了地应力分布，与层位解释的结果相对照，基本吻合大断裂的走向，并且还表征出了一些小型断裂，可以验证本文计算方法在实际应用中的合理性。

综合比较来看，基于曲率的地应力表征只能提供应力和裂缝的分布状况，但是不能指出地应力的定量关系，并且对于分布趋势的表示比较模糊，由曲率方法计算得到的地应力同样展示了地应力分布，也对地应力进行了定量计算，但是由于在砂泥岩中层位的均匀性和连续性较差，计算的曲率可靠性相对较低。相比于传统的基于井点模型应力计算方式，新的计算方式去除了重力的影响，对水平应力有更客观的表示，同时正交各向异性模型下计算的地应力由地震反演参数而来，与实际地质情况相符合，得到的大小关系可靠性较高。纵向上，选取井曲线进行了垂向上的比较，运用层位解释成果进行了层位上的验证，体现了本文提出的地应力计算方法的准确性与合理性。从变化趋势、整体分布、可靠性等多方面来看，正交各向异性模型下计算的地应力具有明显的优势。

图6 正交各向异性模型下差应力之比的层位切片(左图)和A井测井曲线同差应力计算结果对比(右图)

图7 目的层断层解释图(黑色线为断层线)

5 结论

文章探讨砂泥岩情况下的地应力表征方法，采用叠前地震地震反演，获得了弹性参数和裂缝弱度参数，通过参数转换得到了各向异性参数，通过从构造角度计算出了曲率分布，结合曲率与应力的关系，计算了基于曲率的地应力分布情况。建立了正交各向异性模型，计算出了地应力差异比，还采用传统的井点模型来计算了地应力，经过不同角度的比较、分析与评估，得到了砂泥岩介质下地应力表征的一种方法，新方法具有明显的优势，能够更好地表征水平方向上的应力分布，证明了正交各向异性模型应力预测方法在砂泥岩层中适用，对未来油气藏的勘探开发有着重要的意义。