基于云台的变域论模糊PID算法研究

苏小会， 许 培， 陈毅维

(西安工业大学 计算机科学与工程学院，西安 710021)

0 引言

云台应用领域广，品类渐多，功能复杂。但是存在几个较为严重的问题，如单自由度，云台变动范围受限；采用低端MCU或单片机，性能受限；采用开环控制调节位置，并且无反馈，增加了人工工作量；速度无法实时调节，精确度不高等[1]，这需要从算法和控制策略上进行改进。

目前解决云台响应速度和平衡精确度问题使用的是PID算法，由于不同控制系统的特点不同，对PID响应速度和稳定性的要求也不同[2]。常用PID算法分为以下几种[3]：位置式PID算法：它将每次误差进行累加作为积分，运算量较大，且每次输出均与过去的状态有关；缺点为可能引起大幅度超调[4]。积分分离式PID算法：在PID控制中引入积分环节可以消除稳态误差。但在启动、结束或大幅度更改设定值时，积分输出可能会引起较大超调甚至震荡，所以在误差较大时屏蔽积分环节，当误差小于一定范围时，引入积分控制，使得偏差较大时确保响应速度偏差较小时确保精度[5]。变速积分PID算法：基本思想是设法改变积分项的累加速度，使其与偏差大小相对应：偏差越大，积分越慢，反之则越快[6]。

基于以上算法的缺陷和不足，本文提出了一种变域论模糊PID算法。该算法的原理是在传统PID控制算法的基础上增加模糊控制器，模糊控制器用于产生能兼顾控制系统动态特性与静态特性、实际输出与干扰抑制之间变化的参数优化量，从而提升控制系统的整体性能[7]。变论域模糊自适应PID控制算法是在模糊自适应PID控制算法基础上，增加变论域控制器而实现的。

1 云台结构原理

图3 变论域模糊自适应PID算法控制过程

如图1，整个系统由主控制器、执行机构和姿态感知机构组成。实线箭头代表控制信号输出方向，是主控制器和执行模块组成的步进电机控制机构；虚线箭头代表数据、指令信息流动的方向，是由主控制器和姿态感知机构组成的闭环姿态反馈机构[8]；主控制器和PC之间由加粗的实线箭头连接，支持串口、网络两种形式的数据交换，一方面PC可以作为数据输出的终端而便于程序的观察调试，另一方面，也可以在PC上通过远程连接或者串口调用云台控制程序。

主控制器采用基于ARM920T核的S3C2440芯片，本文使用2个PWM定时器并2个GPIO口，分别用于提供步进电机驱动器所需的脉冲和方向信号；通过I2C接口将MPU6050的数据读取到主控制器[9]。

图2是主控器与电机驱动器连接图。主控制器共使用4个引脚与步进电机驱动器(执行机构M542)相连，其中GPB0和GPB1引脚用做Timer，使用Timer0和Timer1的PWM功能，形成供步进电机转动的脉冲信号；GPF0和GPF1引脚设为输出模式，输出高、低电平控制步进电机的转动方向。M542的PUL+和DIR+共接+5 V电源，使能信号ENA-和ENA+置空，则电机恒使能。

图2 主控制器与电机驱动器连接图

姿态感知机构使用MPU6050芯片，它是一款被整合的6轴运动传感器件，内置3轴陀螺仪，3轴加速计和1个DMP(digital motion processor)硬件加速引擎，提供1个用于与第三方数字传感器相连的辅助I2C接口，如磁力计，压力计等。当与第三方3轴传感器连接时，MPU6050以其主I2C接口实现完整的9轴数据输出[10]。

为了使得云台硬件达到快速响应和精确控制的目的，提出了基于云台的变域论模糊PID算法。

2 变论域模糊自适应PID算法

2.1 变论域模糊自适应PID控制算法的组成

模糊自适应PID控制算法是在传统PID控制算法的基础上增加模糊控制器实现的，模糊控制器用于产生能兼顾控制系统动态特性与静态特性、实际输出与干扰抑制之间变化的参数优化量，提升控制系统的整体性能，见图3(a)，它由模糊器、规则库、模糊推理机、解模糊器几个部分共同组成。变论域模糊自适应PID控制算法同模糊自适应PID控制算法目的一样，也是为了产生能改善系统性能、提高系统应对复杂问题能力的参数优化量；不过变论域模糊自适应PID控制算法是在模糊自适应PID控制算法基础上，增加变论域控制器而实现的，见图3(b)。

模糊控制器是一个2输入，3输出系统，输入量为偏差e，偏差变化率ec，输出是作为PID控制器各项系数存在的参数kj(j=p,i,d)的优化量Δkj。参数优化量的获取只通过模糊控制器即可，依次由模糊器实施模糊化处理、由模糊推理机实施模糊逻辑推理、由解模糊器实施解模糊操作；最终用于PID控制器的参数由参数生成器对基础参数和参数优化量加和求得。

2.2 变论域控制器

变论域模糊控制器用于缩放进出模糊控制器的变量，以达到等效变论域效果的目的。为实现变论域操作，把施加在模糊论域上的缩小操作转变为对于基本论域的缩小，因此要求输入值较小，能够落在缩小后的基本论域中；随后再把该变化转移到系统的输入输出变量上：以论域的缩小和出入值的不变，造成进出系统的值逻辑上的放大，见图4(a)中一虚一实两点，并且论域的缩小使得规则压缩，模糊论域上的某一点会向着表述同一方向的程度更深的自然语言值的模糊子集偏移，即语义程度加深。反之亦然。不过，通常要求在输入与输出值上要进行相反的变论域操作，但是，这并不是绝对的，在某些具有特殊要求的场合可能会要求输入和输出都放大或缩小论域。若论域[e,e]缩小后变为[-e1,e1]，见图4(b)，伸缩因子α=e1/e(0<α<1)，可得到如下论域传递关系式:

(1)

图4 变论域原理图

若x1是最终落在论域[-αE,αE]的输入量，x是经缩小的基本论域[-e1,e1]进入的输入量，则x1=(x/α)·(E/e)是使模糊控制器实现缩小论域操作的等效因子，其中x/α是使得x从论域[-e1,e1]转化到论域[e,e]，可以把缩小论域理解成基本论域不变，直接放大进出系统的值，但放大后该值必需仍在基本论域范围中；E/e是使论域从[e,e]转化到[E,E]固定比例，令E/e=1，则x1=x/α。同理，论域[e,e]放大后变为[-e2,e2]，对于伸缩因子α=e/e2(0<α<1)，可得到使模糊控制器实现放大论域操作的等效因子x2=αx·(E/e)=αx。

(2)

即最终模糊论域不发生改变，只缩放基本论域，缩小基本论域意味着要放大输入、输出量的值，放大基本论域意味着要缩小输入、输出量的值。

以偏差e和偏差变化率ec两个变量作为输入，其输出为αi、βj(i=e,ec；j=p,i,d)，根据需要为模糊控制器的5个变量分别产生伸缩因子，本文针对输入、输出变量分别产生伸缩因子，即令α=αi，β=βj，因α、β分别改变输入、输出的论域而又分别被称为量化因子、比例因子。

输入论域缩小时，论域系数Ke、Kec、KΔkj变化为：

(3)

输入论域放大时，论域系数Ke、Kec、KΔkj变化为：

(4)

为了便于调节模糊控制器的输入输出，会给其输入、输出上乘以分数或倍数，这种变化体现在论域系数上，产生抑制或增强论域缩放的效果。

3 变论域模糊自适应PID算法的仿真

使用MATLAB对模糊自适应PID算法进行仿真，其仿真子系统如图5所示，其中模糊控制器的实现没有改变。为了便于仿真，这里选取伸缩因子α、β为：

(5)

IVUC(输入变论域控制器)，OVUC(输出变论域控制器)，其中VUO1、VUO2(变论域操作)用来实现论域的缩小(除以伸缩因子)与放大(乘以伸缩因子)。

图5 基于函数模型的变论域模糊PID算法仿真子系统

基于模糊控制的变论域控制器，表1为模糊规则的变论域控制器的输出信息α、β。模糊控制器的原始输入值，若进行放缩型变论域操作，即令VUO1～2为乘法使得输入值缩小，令VUO3～5为除法使得输出值放大，就得到模糊控制器的最终输入、输出值；再放大其输出值，便能得到变论域模糊控制器的最终输出。

由于模糊处理过程对模糊控制器进行精确的控制，在变论域控制器采用的模糊规则不大变的情况下，其伸缩因子α、β趋势相对稳定，难以实现在输入端缩小论域而在输出端放大论域，即缩放型变论域的操作。该仿真方法伸缩因子的确定取决于模糊规则的优劣。

表1 变论域控制器模糊规则表(α、β规则相同)

对模糊控制的变论域控制器而言，该仿真方法实现起来较为简单，其伸缩因子受控于所选择的函数模型，可控性强，伸缩因子可通过参数调节，这里默认伸缩因子的参数ε=0.001，E=3，τ=0.5。

当伸缩因子较小时可以进行放缩型变论域操作：此时设置IVUC中λ=0.1，VUO1为乘法，OVUC中λ=0.2，VUO2为除法。伸缩因子α如图6(a)所示，不同于基于模糊控制的情形，此时它是根据e、ec的输入实时计算的，因此有所不同。放大论域使得最终进入模糊控制器的输入如图6(c)所示，与图6(b)相比，输入值的幅值降低，平滑程度增加，抑制了误差。

图6 基于函数模型的放缩型变论域仿真过程中的重要变量

当伸缩因子较大时可以进行缩放型变论域操作：设置IVUC中λ=4，VUO1为除法；OVUC中λ=4，VUO2为乘法。其伸缩因子如图7(a)所示，缩小论域使得最终进入模糊控制器的输入如图7(c)所示，与图7(b)相比，可见缩小论域后的图像幅值有所增加平滑程度降低，也就是说放大了误差。

图7 基于函数模型的缩放型变论域仿真过程中的重要变量

由图8(a)、(b)可以看出，对模糊控制器的输出而言，放缩型变论域控制效果明显比缩放型变论域控制效果好，在图8(c)的仿真结果中也证实了这种观点。

图8 基于函数模型的放缩型、缩放型变论域的模糊控制器输出及控制效果

4 变论域、模糊及传统算法效果比较

(6)

取J=0.066(kg.m2)，B=0.5(N.m.s/rad)，Nr=200，i=3.76 A，Lsr=0.056 mH，得到外框轴传递函数G2(s):

(7)

仿真时的框架如图9，因方法不同而使用不同的仿真子系统，因研究框轴不同而应用不同的传递函数。

图9 仿真方法框架图

图10 变论域、模糊及传统算法效果比较图

仿真时，取Kp=15.15，Ki=78.5，Kd=3.83，Ke=1，Kec=1，Ku=1/3(KΔkj，j=p,i,d)，结果如图10和表2所示，其中vufPID1是基于模糊控制的放缩型变论域方法的输出曲线，vufPID2是基于函数模型的放缩型变论域方法输出曲线。

从表2看出，相比于传统的PID控制算法，两种放缩型变论域方法都取得较好的控制效果，改善了曲线的震荡幅度，加快了曲线的收敛速度，vufPID1仅在稳态误差上有所不及；模糊PID算法对传统PID算法的控制效果的提升相对而言要小得多。

表2 算法效果曲线时域性能指数表

5 测试结果分析

图11是云台测试过程中的角度变化信息。测试采用的步进电机能够响应高达30 kHZ频率的脉冲，根据测试X轴频率不宜超过50 k，Y轴不宜超过6 k。且在电机控制曲线决策的同时修改变速系数，重复云台的运行轨迹时，对X轴和Y轴分别进行运动测试。

图11(a)反映的是没有使用控制曲线的条件下，XY两轴以1 000为控制脉冲的频率，控制步进电机带动云台载物台进行匀速运动时的角度变化情况，此时采用匀速控制策略；图11(b)和图11(c)分别反映的是在使用直线型、S型控制曲线的条件下，XY两轴以1 000为启动频率，变速次数为5，变速系数分别为300和500时，电机带动云台载物台变速时的角度变化情况。

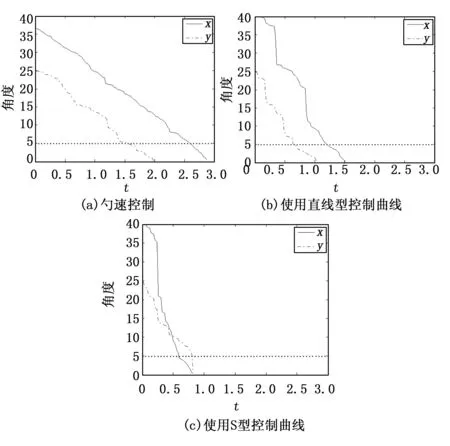
图11 云台实际控制过程角度变化图

图11所示，在匀速运动过程中由于控制频率不高且保持不变，角度随时间变化趋势接近直线，控制过程相对稳定，系统振动幅度不大；且频率相同的情况下，由于Y轴的负载比X轴大，稳定程度不如X轴。

在直线型变速运动过程中，曲线上的骤变点较多，XY两轴的稳定程度相对于匀速运动而言明显降低，速度的提升使得其运动所耗费时间有所降低，所以电机执行加减速过程时，由于速度的变化引起角度的变化出现曲线特征，经减速过程后其角度进入α邻域，此时电机以启动频率匀速向ε邻域运行。

在S型变速运动中，X轴的角度变化趋势呈现S型特征，控制耗时减少，运行过程较直线型运动平稳。而Y轴由于负载原因，运动过程中震荡明显，运动控制紊乱，不能完成既定的控制目标，降低控制参数，使其产生较低的频率时情况改善，但时间上较直线型变速控制不明显。

6 结论

为了使云台能够更快更准确的根据外部环境变化自动调节，本文对变论域模糊自适应PID控制算法进行了深入的研究，重点研究了在传统PID控制算法的基础上增加模糊控制器和变论域控制的功能、原理以及实现方式；以Matlab/Simulink工具进行仿真实验，并对它的伸缩因子展开研究，最后对比了它与传统PID控制算法优劣，结果表明模糊PID算法的控制效果较传统PID控制算法显著提升。在保证动态稳定性的前提下，Y轴的运动时间可以控制在1 s内，定位精度控制在0.7°内，X轴的运动时间可以控制在0.5 s内，定位精度控制在0.5°以内，与传统算法相比较，极大的提高了平台的响应速度，证明本文提出的算法是有效的。从而在一定程度上满足了云台对高速响应、动态稳定、定位精度等能力的要求。